基于改进的偶极子算法对雷击高塔电磁场的计算分析

（洛阳供电公司，河南洛阳471002）

0 引言

雷电现象在全球各地都普遍存在着，每天都会有雷电活动的发生。而随着通信时代的来临，通信铁塔、传输高塔的分布变得尤为广泛，由于尖端放电现象的存在，使得这类高塔建筑物成为了极易遭受雷击的对象，甚至有些高塔全年可能会遭受数十次雷击。计算电磁场的分布，首先需要计算出相应的电流。对于雷击高塔回击电流的计算，通常是基于雷电回击模型。蒋宝忠等[1]讨论了几种主要的回击模型在雷电电磁场计算中的应用。Rakov等[2]定义的传输线模型和由Heidler等[3]在提出的传输电流源模型是被采用较多的模型。Uman等[4]在BG模型的基础上，考虑了通道高度的影响，假设回击电流以速度v无衰减的沿闪电通道传输，提出了传输线（TL）模型。Rachidi等[5]同样对553高塔进行工程模型建模，结果表明，高塔对远场的地面垂直电场和水平磁场都存在明显的增强作用，增强系数均为：ktall=(1-ρt)(c v+1)/(1+ρgr)，其中，ρb是雷击地面时，地面的反射系数。Bermudez等[6]将TL传输线回击模型应用到雷击高塔过程中，研究了高塔对雷电电磁场远场所产生的影响，得出的结果显示，当高塔的高度(h＞tfc/2)时，tf是电流在塔顶和塔底来回反射的周期，高塔对远场的增强因子相对于雷击地面时为；当高塔的高度时，增强因子为(1+ρch-g)（其中ρch-g=(ρb-ρt)/(1-ρbρt)）。Baba等[7]在前面学者研究的基础上推导出了雷击高塔时，远场峰值与塔顶电流的初始峰值、塔顶电流的最大值、塔底电流最大值之间的公式。

因此，正确分析在雷击高塔时高塔周围的电磁环境的分布，是我们采取正确的防护措施的前提。但由于自然雷电在时空的分布上，瞬时变化太快，随机的变量多，很难直接将雷电流测量出来。本文通过对传统的偶极子算法进行改进，将高塔从雷电通道中分离出来，对高塔所产生的电场进行单独计算，同时改进后的模型只考虑了辐射场的作用，因此形式上更为简单。

1 高塔回击电流计算

1.1 高塔底部基电流模型

Pavanello等[8]通过对比由不同的工程模型预测得到的雷电流的时空分布情况，结合Heidler函数模型，给出了一个理想的闪电通道底部的雷电基电流的数值模拟公式：

式中：I01、I02分别为击穿电流和电晕电流的电流峰值；η为电流峰值的修正因子；τ1、τ3分别为击穿电流和电晕电流波形的上升时间，τ2、τ4分别为波形下降时间。在此公式中，雷电流峰值，电流变化率等特征参量可以做到相互独立的由I01、I02、τ1、τ2、τ3、τ4来控制，能够更加准确的描述雷电流波形。图1为相关特征参数取值所作的通道底部的理想雷电流波形，我们使用Rachidi等[9]继后电流的数据，选取I01=9.9kA，η=0.845，τ1=0.072 μs，τ2=5.0 μs，τ3=100.0 μs，τ4=6.0 μs，I02=7.5 kA。从图中电流波形的分布可以看出，波形上升快下降慢，波头时间较短，符合雷电流是一个单极性非周期的脉冲波形的特点，所以此基电流模型能近似地用于雷电流波形的模拟。

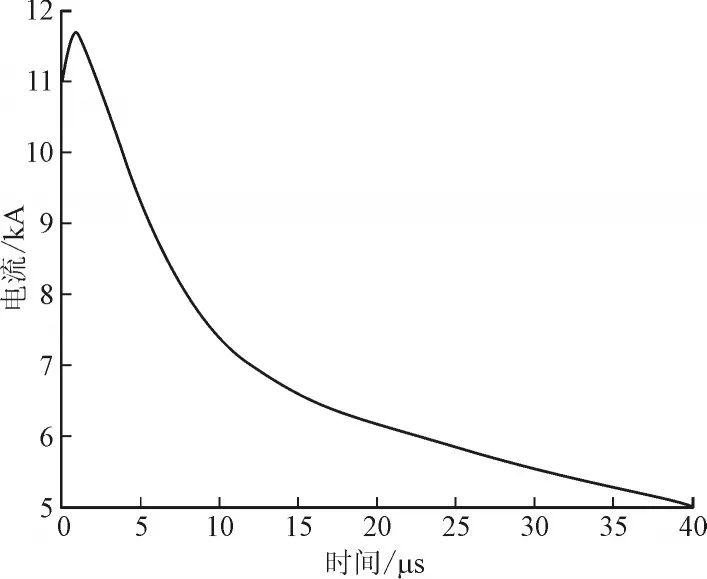
图1 雷电基电流图Fig.1 Lightning base current diagram

1.2 回击电流在高塔内的分布特征

上图为一个理想电流的波形图，即不考虑地面引雷体的反射，但在上面的叙述中我们也讲到，在实际情况中，高塔两端与闪电通道和大地之间的阻抗不同，因此存在着一定的反射系数，电流会在高塔顶部和底部发生反射。考虑雷电流在通道内的反射，不考虑回击通道和高塔的形状，将高塔和雷电通道分别看成是两端具有一定等效阻抗和接地阻抗的均匀无损传输线，并假设在塔顶和回击通道底部的连接处存在理想电流源，推导得出以下高塔作为引雷体时，回击电流分布仿真的计算公式：

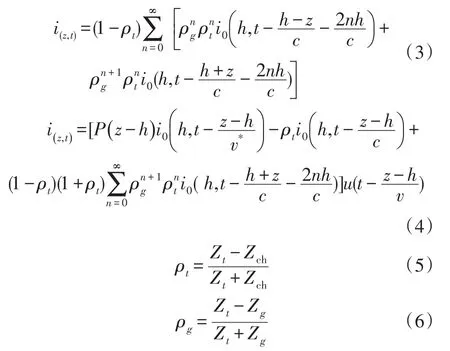
式（3）中，0＜z＜h（塔内）；式（4）中，h＜z＜H0（雷电通道内）；Zt、Zg、Zch分别为闪电通道的等效阻抗、接地系统的等效阻抗和地面引雷体的特征阻抗；c 为光速，P（z）是不同模型所对应的衰减函数，u（t）为阶跃函数，v是回击前沿的速度，v*是电流波的速度，n是回击电流在塔顶和塔底来回反射的次数，z是某一点的高度。图2给出了我们考虑反射时，使用几何法计算电流和电场的参考图。

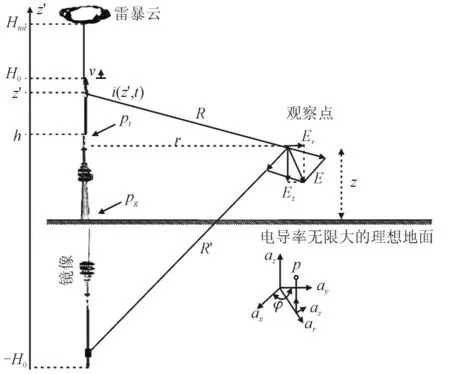
图2 几何法进行场的计算Fig.2 The calculation of the field by geometric method

假设参数的取值为：塔高h=168 m，反射系数ρt=-0.53，ρg=0.7。我们利用式（3）和式（4）可以得出图3，它们分别对应为塔顶电流和塔底电流。图3（a）塔底电流在1.8μs左右出现了峰值，这是在这个时刻，回击电流到达塔底，由于塔底对电流存在反射作用，反射电流与标准电流同时出现在塔底，相互叠加，所以塔底回击电流出现了最大的电流峰值与最短的波头时间，波头陡度最大。图3（b）塔顶的继后电流变化初始阶段与标准电流近似，但到达峰值时间时间大约在3.9μs左右，塔顶峰值明显比标准电流大了10 kA左右，这是由于塔底反射电流传输到达塔顶，从而导致塔顶出现峰值。从图中模拟出的电流波形可以看出高塔底部的电流峰值要远大于高塔顶端的电流峰值，这是由于地面向上反射的雷电流在塔底产生的叠加效果。另外从图中我们可以看出，考虑到塔顶和塔底的反射之后所计算得到雷电流波形，明显存在一定的波动，在上升和下降的过程中均有一定的反复，这便是电流在通道内的反射对电流波形造成的影响。

2 雷击高塔产生的辐射电场优化计算

2.1 传统偶极子技术计算

在计算回击电磁辐射场时，我们通常采用如图2所示的几何法进行运算。图中，我们可以将雷电回击通道和高塔均近似地理解为一段长为Htot的垂直于地面的竖直天线。计算时，我们假设地面为大地电导率无穷大的理想地面，假设回击电流在通道的分布是均匀的，回击电流以速度v沿着雷电回击通道向上传输，在电流的回击高度h的上方，电荷和电流均为0，将通道放入柱坐标系中来计算电磁场。

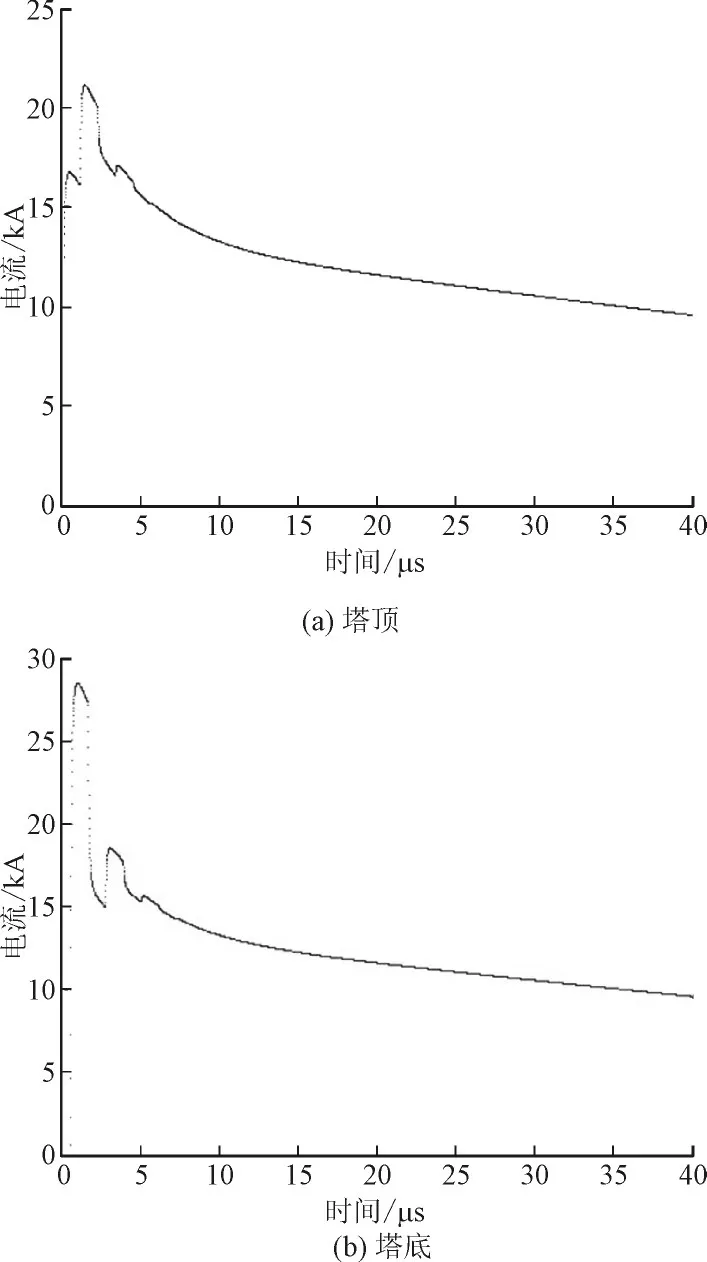
图3 考虑杆塔反射时塔顶、塔底电流波形Fig.3 Current waveforms at the top and bottom of the tower when the tower is reflected

通过解麦克斯韦方程组，Master[10-13]得到高度z′处电流在P点产生的电场计算公式：

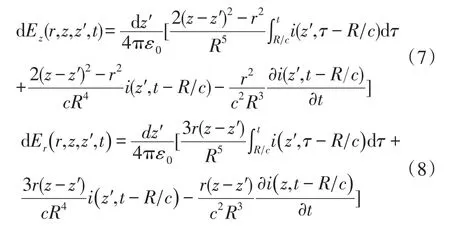
式中，r和z是观测点的柱面坐标，R是在通道上一点与观测点之间的距离是通道电流表达式，c为光速，ε0是真空电容率，可由公式代入计算。

2.2 优化公式计算

首先，我们需要简化几何法的示意图，如图4所示，我们假设地面为大地电导率无限大的理想地面，观测点在地面P处，距高塔的距离为d。我们已经知道在TL传输线模型中，我们可以将高塔看成是一段长为l，垂直于地面的竖直导线。

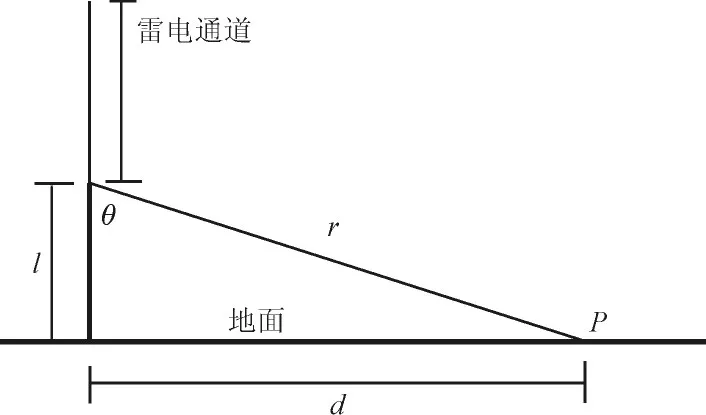
图4 计算雷击高塔时所产生的电场简化示意图Fig.4 A simplified schematic of an electric field generated by a lightning strike tower

在雷电通道与高塔的连接点处，雷电流将同时进入高塔内部和雷电通道中进行传输，其中，进入高塔内部被激活的电流源将以光速沿着高塔向下传输，在电流到达地面时，电流可能会被大地完全吸收，也有可能部分吸收或者是完全反射，这取决于高塔两端的反射系数。反射系数为0，则代表完全吸收无反射；反射系数为1，则代表完全反射无吸收。当我们假设回击速度接近光速时，由通道内电流在某一点所产生的辐射场即为通道在该点所产生的总电场。因此我们计算在高塔在P点产生的电场时只需要计算它的辐射项就可以了。

当我们先不考虑高塔的反射系数时，电流脉冲到达地面后将被地面完全吸收，由于电流的传输速度为光速，因此高塔在P产生的总电场由两部分辐射场组成。其中一个是电流进入高塔顶部时，在P点产生的辐射场；另外一个则是当电流在高塔底部被地面吸收时所产生的辐射场，这两部分辐射场的和即为总电场。

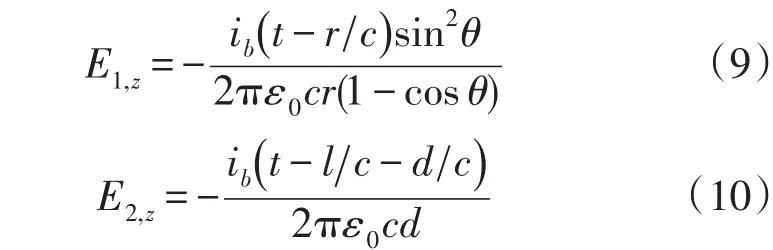
式（9）和式（10）分别为高塔顶端与底部在P点所产生的辐射场的计算公式，式中ib(t)为高塔顶部接入的电流函数。同时在电流接入高塔时，我们应当要记住，会有一个相同大小带着正电荷的电流进入雷电通道中向雷暴云进行传输，这一部分的电流也会在P点产生一个电场。r为高塔顶部到观测点P之间的距离。

把公式（9）与公式（10）相加即为P点处的总的电场，但我们在利用Matlab进行运算时，需要考虑到这两个辐射场到达P点时是存在一个延迟的，因此我们计算时需要对时间变量t进行讨论。

接下来我们考虑高塔存在着一定的反射系数，但是由于反射只会存在于高塔的上下两个端点，而此优化方法是根据加速电荷的理念来进行电场的计算，因为速度的改变只会发生在发生反射的部位，所以我们依旧是可以将高塔产生的总电场分为两个部分来计算。假设高塔顶端的反射系数为ρt，底部的反射系数为ρg，为了方便计算，我们可以假设，当高塔内回击电流沿高塔传输到达顶部时，电流先由顶部完全吸收，然后在P点产生一个辐射场：

然后，我们考虑到顶部的反射系数，这时将有所占比例为ρt的电流被反射，沿高塔向下传输，所占比例为（1-ρt）的电流部分将沿雷电通道向上传输，于是我们可以得到向下传输的这部分电流在P点处产生的辐射场的大小：

由于回击电流在高塔两端的反射不止一次，因此结合公式（9）-（12）我们可以推广出n次反射之后，塔顶反射的向下传输的电流在P点处产生的辐射场为

底部回击电流向上传输被塔顶吸收的部分在P点处产生的辐射场为

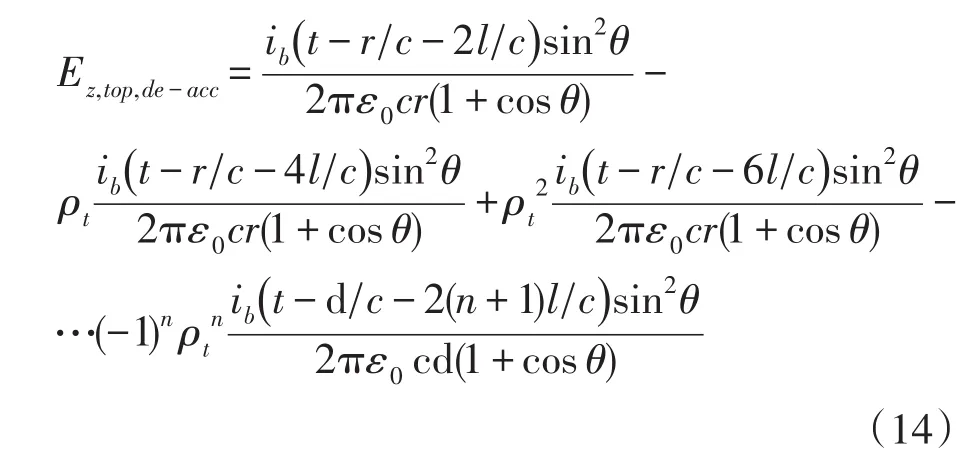
底部吸收的向下电流在P点处产生的辐射场为

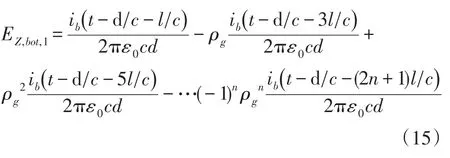
底部反射的向上电流在P点产生的辐射场为

对于闪电通道内回击电流在P点产生的电场，我们可以认为是由一段，速度从0变化到u的电流所产生的辐射场，速度u为通道内电流的回击前沿速度，因此我们可以用下面这个公式来优化通道产生的辐射场[14-15]：

在公式（13）至式（17）中n为回击电流在高塔两端反射的次数，从理论上讲n的最小值能取到0，但我们一般进行模拟计算时，n的取值至少取到100。公式（13）至式（17）的总和计算所得的即为雷击高塔时在P点处产生的总电场。本文采用公式（3）至式（4）高塔顶端的电流ib(t)为标准基电流，模拟杆塔高度为168 m，杆塔反射系数ρt=-0.53，ρg=0.7，分别计算距离杆塔50 m、5公里处的电场变化趋势（图5、图6）。从图中可以看出，电场的总体变化与电流变化相关，电场变化主要集中在前5秒内，并且上升与下降的波动都极为明显。由于雷电流在高塔两端不断发生反射，导致塔内电流在这段时间内发生震荡现象，从而导致高塔周围的电场也在这段时间内发生了明显的波动。上述公式存在几个优点，1）我们能成功的将高塔从雷电通道中分离出来，对高塔所产生的电场进行单独计算，这样我们可以单独对高塔所产生的影响进行研究。2）从表达式上来看，此模型只考虑了辐射场的作用，因此形式上更为简单。3）在最终结果的模拟上来看，利用此模型对电场的计算结果与其他方法一致，证明了模型的正确性。

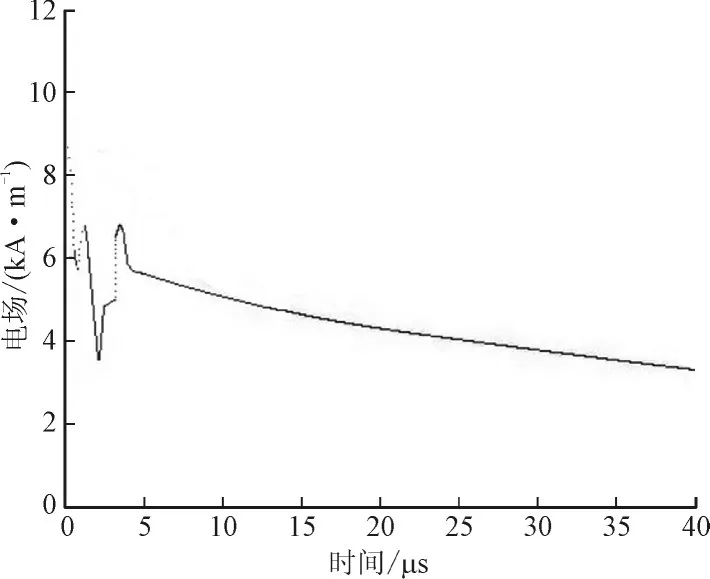
图5 高塔在P点产生的总电场（h=168 m，d=50 m，ρt=-0.53，ρg=0.7）Fig.5 The total electric field generated in the tower P（h=168 m，d=50m，ρt=-0.53，ρg=0.7）

图6 高塔在P点产生的总电场（h=168 m，d=5 km，ρt=-0.53，ρg=0.7）Fig.6 The total electric field generated in the tower P（h=168 m，d=5 km，ρt=-0.53，ρg=0.7）

3 结语

利用改进模型计算高塔周围电磁场的方法相对于传统的偶极子法，所得到的结果一致，但是却拥有计算简单，模型更易理解操作的优点。笔者改进算法考虑的回击模型是基于TL传输线模型，假设回击速度接近于光速，然后将电场的静电项、感应项和辐射项简化为只考虑电场的辐射项，根据加速电荷的理念，电流在塔顶和塔底发生反射，电荷在塔顶和塔底发生加速或减速，从而在距离高塔一定距离处产生一个辐射电场，我们将此辐射电场就可看为高塔所产生的总电场。因为只需要考虑高塔的两端，所以不需要进行大量的积分计算，对于回击模型为TL模型时，此方法的计算将更为简便，并且结论的一致性证明了此方法拥有实际意义。

[1] 蒋宝忠，滕欢.雷电回击模型在雷电电磁场计算中的应用分析[J].四川电力技术，2010，33（2）:38-41.

JIANG Baozhong，TENG Huan.The application and analysis of lightning strike model in the calcu⁃lation of lightning electromagnetic field[J].Sichuan electric power technology，2010，33（2）:38-41.

[2] RAKOV V，UMAN M.Review and evaluation of lightning return stroke models including some aspects of their appli⁃cation[J].Electromagnetic Compatibility IEEE Transac⁃tions on，1998，40（4）:403-426.

[3] HEIDLER F，CVETIC J M，STANIC B V.Calculation of lightning current parameters[J].IEEE Transactions on Pow⁃er Delivery，2002，14（2）:399-404.

[4]RUBINSTEIN M，UMAN M A.UMAN M A.:Methods for calculating the electromagnetic fields from a known source distribution:application to lightning.IEEE Trans.Electro⁃magn.Compat.31（2），183-189[J].IEEE Transactions on Electromagnetic Compatibility，1989，31（2）:183-189.

[5]RACHIDI F，RAKOV V A，NUCCI C A，et al.Effect of ver⁃tically extended strike object on the distribution of current along the lightning channel[J].Journal of Geophysical Re⁃search Atmospheres，2002，107（D23）:ACL 16-1-ACL 16-6.

[6] BERMUDEZ J L，RACHIDI F，RUBINSTEIN M，et al.Far-field-current relationship based on the TL model for lightning return strokes to elevated strike objects[J].IEEE Transactions on Electromagnetic Compatibility，2005，47（1）:146-159.

[7] BABA Y，RAKOV V A.Lightning strikes to tall objects:Currents inferred from far electromagnetic fields versus di⁃rectly measured currents[J].Geophysical Research Letters，2007，341（19）:255-268.

[8]PAVANELLO D，RACHIDI F，RAKOV V A，et al.Return Stroke Current Profiles and Electromagnetic Fields Associ⁃ated with Lightning Strikes to Tall Towers:Comparison of Engineering Models[C].International Conference on Light⁃ning Protection，ICLP 2004.2004.

[9] RACHIDI F，RAKOV V A，NUCCI C A，et al.The Effect of Vertically-Extended Strike Object on the Distribution of Current Along the Lightning Channe[J].Journal of Geo⁃physical Research Atmospheres，2002，107（D23）:ACL 16-1-ACL 16-6.

[10]MASTER M J，UMAN M A.Transient electric and magnet⁃ic fields associated with establishing a finite electrostatic dipole[J].American Journal of Physics，1991，51（51）:118-126.

[11]郄秀书，张其林，袁铁，张廷龙.雷电物理学[M].北京：科学出版社，2014:1-2

[12]UMAN M A.The art and science of lightning protection[M].Cambridge University Press.2008:3-20.

[13]弗拉迪米尔A.洛可夫，马丁A.乌曼.雷电[M].张云峰，吴建兰，译.北京：机械工业出版社，2016：85-87

[14]崔逊.全球闪电定位系统_WWLLN_探测效率和探测精度评估[D].南京信息工程大学，2013.

[15]FINKE U，KREYER O.Detect and locate lightning events from Geostationary Satellite observations[R].Report part I:Review of existing lightning location systems，September 2002:3-17.