变转速回转筒内二元颗粒混合特性数值分析
张立栋,程 硕,李少华,王 擎,徐向明,刘 斌
(1.东北电力大学油页岩综合利用教育部工程研究中心,吉林吉林132012;2.抚顺矿业集团有限责任公司 页岩炼油胜利实验厂,辽宁抚顺113001)
颗粒物料在化工、能源等行业过程中被广泛应用,工业设备的作业对象或工作介质常常涉及到离散颗粒物料[1~2].回转筒是输运和处理颗粒物料的重要设备,如干燥过程[1],热解干馏[3~4],颗粒混合[5~6]等,颗粒物料在回转筒中的接触关系和动态响应特性直接影响工业装备的工作效率,深入研究颗粒物质在回转筒内的运动规律具有很高的应用价值[7].
影响颗粒物料在回转装置内混合过程的因素主要有物料的物理性质、混合器的结构形式和操作条件三个方面.在物料的物理性质方面,主要是通过研究不同颗粒密度比和粒径比,如陈辉等[8]采用离散单元法研究的两种颗粒密度分别为1 450 kg/m3和574 kg/m3,密度差达到2.5倍;黄德财等[9]对3种不同颗粒密度比(3∶1,5∶1,9∶1)的二元等直径颗粒在回转装置内的混合与分离数值模拟研究;Xu等[10]研究二组元非等粒径颗粒的密度比为10∶1在回转装置内的混合.在混合器的结构形式方面,用圆形[5~10]、椭圆形[11~15]、正方形[14~15]、波纹型滚筒[17]等准二维旋转混合器内颗粒的偏析与混合,在这其中研究圆形滚筒的较多.以上研究颗粒在回转滚筒中运动或混合时均是对比分析不同滚筒转速下进行的,其某一工况下滚筒转速是没有改变的.
对于颗粒混合在回转滚筒中运动特性,在单一改变操作条件时,在筒内颗粒的混合达到稳定之后,所得到的混合指数会在某一个值上下波动,易产生混合的规则区.因此,本文提出采用滚筒转速随时间连续变化的变转速工况,采用离散单元法研究对2种粒径但密度相同的颗粒在椭圆形滚筒及圆形滚筒(分别以椭圆形滚筒的长短轴作为直径)的变转速工况下,对比分析三个滚筒内非等粒径二元颗粒体系的运动混合过程.
1 实验装置及仿真工况设定
1.1 仿真工况设定
设计三种不同结构的回转筒模型,如图1所示.图1(c)为椭圆形滚筒,长轴D1为94 mm,短轴D2为76 mm,图1(a)、图1(b)分别以椭圆滚筒的长轴和短轴为直径的圆形滚筒,称之为长轴滚筒和短轴滚筒,三者筒宽均为8 mm.所选两种颗粒直径分别为3 mm(大颗粒)和1 mm(小颗粒),颗粒数量分别为150和4 020,密度均为1 800 kg/m3,详细的模拟参数见表1所示.

图1 数值模型构造

表1 模拟所需参数
滚筒转动速度随时间变化如图2所示,转速变化从最低的0 rad·s-1,到能使颗粒在滚筒内达到离心运动状态的22 rad·s-1,速度范围涵盖颗粒群运动的所有模式.从滚筒开始转动到25s内滚筒维持恒定转速以使颗粒运动达到稳定运动状态,其后滚筒转速经历加速转动、减速转动和振荡阶段.
1.2 实验与数值对比实验验证
前期分别对圆形滚筒[17]及椭圆形滚筒[12]进行实验及数值研究的混合斑图对比工作.颗粒粒径均是1 mm颗粒和3 mm颗粒,转速恒定.图3(a)为在填充率为1/3的回转滚筒内颗粒离散元模拟,图3(b)为离心率0.6的椭圆形滚筒内二组元颗粒混合斑图对比,从圆形和椭圆形滚筒的实验及数值研究对比来看,颗粒在滚筒中的偏析现象较为相似.
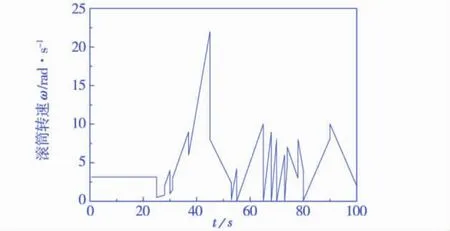
图2 滚筒的旋转速度

图3 实验和模拟过程对比
2 数值计算与结果分析
2.1 颗粒群运动分区分析
根据颗粒在变转速滚筒中的运动状态可将其划分不同区域.滚筒转速在1.7 rad·s-1时,颗粒群分为2个区域,如图4(a)、图4(d)所示.绿色区域的颗粒速度较大,向下作滚落运动,称为流动区;蓝色区域的颗粒运动速度非常低,称为相对静止区.滚筒转速为3.3 rad·s-1,但颗粒群仍处于滚动混合模式时[17],如图4(b)、图4(e)所示.颗粒群的动态安息角[18]变大,从相对静止区进入自由表面流的颗粒在筒壁剪切作用下获得更多的动能和重力势能,快速流动的颗粒增多,因此,流动区相应变大.相对静止区的底部由于受到滚筒壁的剪切加速,颗粒速度增大,部分相对静止区过渡成稳定区;滚筒转速继续增大到8.1 rad·s-1,颗粒群进入抛落模式,相对静止区继续减小且边界变得模糊,稳定区增大,如图4(c)、图4(f)所示.从稳定区出来的颗粒由于速度较大,脱离自由下滑面形成抛物运动,流动区变成抛落区.

图4 不同转速下圆形滚筒内颗粒速度分布

图5 不同转速下圆形滚筒内颗粒运动分区示意图
因此,圆形筒在加速运动过程中,内部颗粒体系运动模式主要经历图5(a)、图5(b)、图5(c)所示过程.相对静止区的颗粒速度低,位移小,基本不发生混合.稳定区的颗粒随滚筒壁一起运动,但其位于颗粒群底部,受到上部颗粒的挤压,径向位移较小,因此混合不会有较大的波动.而在流动区或抛落区,由于颗粒在下落过程中速度不断变化,对流和扩散混合机制作用明显,是颗粒群发生混合的主要区域.因此,各区域所占比例的大小影响颗粒混合效果,而滚筒转速又是影响颗粒群区域划分的主要机制.所以,滚筒转速对颗粒混合起主导作用.

图6 不同转速下椭圆形滚筒内颗粒运动分区示意图
由于颗粒数一定,长轴筒相对于短轴筒填充率较低,导致其相对静止区变薄,流动区和抛落区变长,增加了颗粒的混合.椭圆筒转动时长短轴交替变化,颗粒运动相对复杂.当颗粒运动到图6(a)、图6(b)、图6(c)位置时,相对短轴滚筒,相同转速下椭圆筒壁线速度较大,稳定区的颗粒速度大于短轴筒颗粒速度,但颗粒混合区域即流动区和抛落区变短,所以混合效果低于短轴滚筒.而颗粒运动到图6(d)、图6(e)、图6(f)位置时,其流动层和抛落层相对于长轴筒变长,此时的混合效果大于长轴筒.因此,由于椭圆筒运动时长短轴交替变化的特性,其混合效果变化幅度较大.
2.2 颗粒群运动矢量图分析
图7为变转速滚筒中颗粒群的宏观运动矢量图,大颗粒用红色表示,小颗粒用蓝色表示.图中四个速度是根据颗粒群由分层到混合再到分层的演变过程中出现特定现象确定的.以短轴筒为例,滚筒转速较低时,颗粒运动为间歇坍塌模式,大颗粒通过流动区在碰壁之前具有更大的动能,更容易冲到筒体底部在坡底堵塞堆积,形成静态堆积区即Ⅰ区所示位置.随着滚筒转动,堆积的大颗粒运动到Ⅱ区,由于筒壁剪切作用较小且受到上部小颗粒群的压制围限,堆积区不会发生较大变化.堆积颗粒在Ⅲ区再次进入流动层进行坍塌流动,促成堆积结构的周期性演化.因此当滚筒转速低于某一临界速度时,由于间歇坍塌作用造成局部区域大小颗粒分离,二元颗粒体系易形成结构不规则的花瓣斑图[20].同样,长轴筒和椭圆筒在较低转速下也会产生这种斑图,但是长轴筒填充率较低,椭圆筒在旋转过程中长短轴交替作用造成大、小颗粒速度的交替变化,所以长轴筒和椭圆筒内颗粒的斑图不够明显且更不规则.因此,无论是长、短轴圆筒还是椭圆筒,低转速下二组元颗粒的花瓣运动模式使颗粒产生偏析作用,不利于颗粒的混合.
随滚筒转速的提高,花瓣逐渐消失,颗粒运动进入滚落模式,如图7(b)所示,颗粒物料运动呈图5(b)形式.颗粒混合通过流动区与稳定区中颗粒的不断交换来实现,相对静止区是抑制颗粒混合的区域,又被称为混合死区,所以滚落模式下筒内颗粒的混合效果一般.从图7(c)可知,滚筒转速继续增加,筒壁对稳定区大颗粒的剪切作用增大,导致大颗粒速度增加,间隙变大,死区中的小颗粒向大颗粒空隙扩散,发生颗粒尺度的相互穿插和渗透,这种扩散混合是造成颗粒微观尺度混合的重要作用机理.当滚筒转速大于临界速度时,由于离心作用,二元颗粒都分布于筒壁,且大颗粒在内侧小颗粒在外侧,不同颗粒群再次发生完全分离,混合效果最差,如图7(d)所示.

图7 不同滚筒内二元颗粒运动矢量图
三种滚筒从低速到高速的转动过程中,分离的颗粒物料开始混合,大颗粒从物料的外围逐渐向内部运动,小颗粒则从物料的死区向外部扩散直到颗粒物料再次分离.在某一速度下,两种颗粒相互穿插渗透作用最大时,混合效果最佳.所以滚筒变转速的研究对确定颗粒混合最优时筒体的转速范围具有很好的指导意义.
2.3 颗粒混合过程的定量分析
定量描述颗粒的混合程度,目前常用的评价指标有标准偏差、混合质量、统计焓、变异系数、Lacey混合指数等.而Lacey指数法[21~22]适合评价径向混合,公式为
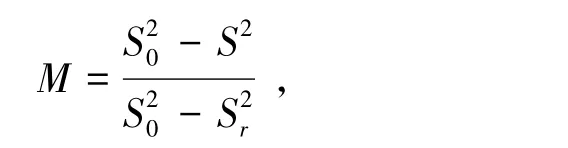
其中:S2为两种颗粒的实际混合方差;为两种颗粒完全分离时的混合方差;为两种颗粒完全混合(理想状态)时的方差.
为得到Lacey混合指数M,根据滚筒和颗粒的尺寸将筒体划分成10×10×1的网格进行统计分析.两种颗粒在不同滚筒内变转速状态下混合指数随时间的变化图,如图8所示.从图8可知,三种筒的混合曲线总体趋势基本相同.25 s前,滚筒处于速度为πrad·s-1匀转速阶段.开始混合指数呈近似线性增加,并快速达到一个相对稳定的混合状态.随后混合指数M围绕某一值上下震荡,因为混合进行到一定程度时,混合和偏析的相互作用达到动态平衡,与文献[21]采用Lacey指数分析圆形滚筒内颗粒运动的实验结果趋势相同.此时,椭圆筒和短轴筒的M值差别不大,而长轴筒的M值高于两者,说明匀速状态下,二元颗粒在长轴筒中的混合效果优于椭圆筒和短轴筒.由于颗粒数不变,长轴筒的填充率相对较小,混合时流动区或抛落区变长,相对静止区变薄,所以其混合度较高,即定量地验证前述运动分区的观点.椭圆筒的填充率小于短轴筒,但M值并没有比小滚筒的M值高,说明椭圆筒在匀速阶段并不能达到增混的效果.
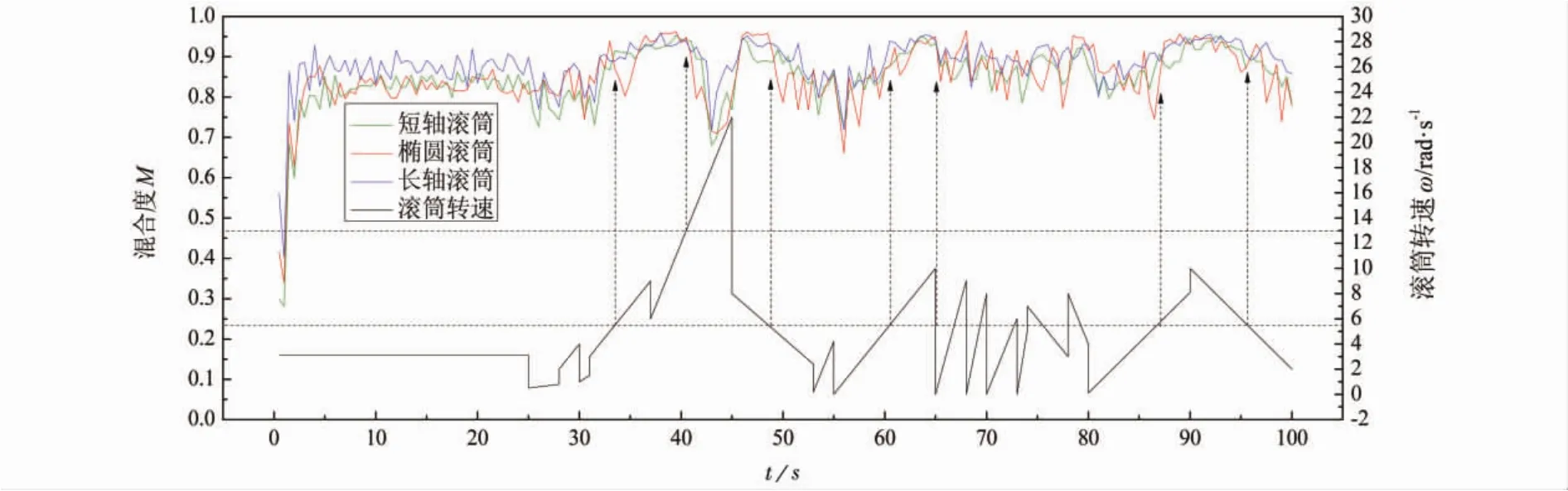
图8 不同滚筒内颗粒混合效果与滚筒转速对比图
随后滚筒进行阶段性变转速滚动,除42 s~45 s内由于筒体转速过快,混合指数偏低外,其余时间颗粒的混合指数基本保持在与前25 s匀速阶段相当或大于匀速阶段.此外,长轴筒M值仍大于短轴筒且椭圆筒混合曲线的振幅明显增大.因此,颗粒数一定时,无论是匀速还是变转速滚动,长轴筒的混合效果始终优于短轴滚筒.椭圆筒在变转速阶段混合度的波动幅度大于匀速阶段的波动幅度.滚筒筒形对二元颗粒的混合具有一定的影响,但筒体转速对二元颗粒混合的影响占主导.
65 s~80 s滚筒转速进行振荡波动,混合指数也产生较大波动.因为滚筒转速的不断变化,导致内部颗粒无序运动增加,颗粒混合时,对流、剪切、扩散三种混合机制在不同转速下交替起主导作用,混合不断变化.同时,颗粒的偏析作用一直存在,混合与偏析交替主导,导致混合指数的较大波动.振荡状态下,三种筒混合指数的平均值分别为0.871、0.881、0.901,而这个阶段滚筒平均转速的混合指数分别为0.8 41、0.836、0.896.对比发现,滚筒速度的变化,能够减少匀速转动时产生混合的规则区,具有一定的增混效果,但是效果不够明显.
根据混合指数较高区域的数值(如图8中两个箭头之间区域),可以得出,颗粒混合效果最好阶段时滚筒的转速范围为5.6 rad·s-1~13 rad·s-1(如图8中两条横虚线之间的速度).在这一转速范围内,三种滚筒内颗粒的混合都是处于图5的抛落模式.因此,筒内颗粒体系呈现出抛落形式时,混合效果较好.
3 结 论
采用离散单元法模拟研究了转速连续变化的情况下3个滚筒内二元颗粒的运动特性,及滚筒的变转速转动对二元颗粒混合的影响.得出结论如下:
(1)滚筒在不同转速下,内部颗粒运动到不同的区域具有不同的运动状态,无论是短轴筒、长轴筒还是椭圆筒,最佳混合工况下的颗粒运动都处于抛落的运动模式.
(2)在颗粒物料一定的工况下,无论是匀速还是变转速滚动,长轴筒混合效果始终优于短轴筒,而椭圆筒混合度的波动幅度较大,混合的稳定性较差,没有达到明显的增混效果.
(3)滚筒筒形对二组元颗粒的混合具有一定的影响,但滚筒转速的影响占主导;且一定速度范围内筒体转速的变化可增强混合.
[1] 黄志刚.转筒干燥器中颗粒物料流动和传热传质过程的研究[D].北京:中国农业大学,2004:35-56.
[2] 王瑞芳,李占勇,窦如彪,等.水平转筒内大豆颗粒随机运动与混合特性模拟[J].农业机械学报,2013,44(6):93-99.
[3] 王擎,肖冠华,孔祥钊,等.固体热载体干馏桦甸油页岩试验研究[J].东北电力大学学报,2013,33(5):15-21.
[4] 柏静儒,张庆燕,白章,等.油页岩固体热载体综合利用系统的分析模型[J].东北电力大学学报,2017,37(1):18-23.
[5] 张立栋,李少华,朱明亮,等.回转干馏炉内抄板形式与双组元颗粒混合过程冷模数值研究[J].中国电机工程学报,2012,32(11):72-78.
[6] I.Figueroa,W.L.Vargas,J.J.Mc Carthy.Mixing and heat conduction in rotating tumblers[J].Chemical Engineering Science,2010,65(2):1045-1054.
[7] 马征,李耀明,徐立章.农业工程领域颗粒运动研究综述[J].农业机械学报,2013,44(2):22-29.
[8] 陈辉,赵先琼,刘义伦,等.转筒内D型二元颗粒物料滚落模式的径向分离[J].农业机械学报,2015,46(6):334-340.
[9] 黄德财,冯耀东,解为梅,等.颗粒密度对旋转筒内二元颗粒体系分离的影响[J].物理学报,2012,61(12):124501-1-7.
[10] Y.Xu,C.Xu,Z.Zhou,et al.2D DEM simulation of particle mixing in rotating drum:A parametric study[J].Particuology,2010,8(2):141-149.
[11]张立栋,朱明亮,刘朝青,等.颗粒在椭圆形回转干馏炉内运动分析[J].化工机械,2014,41(1):34-38.
[12]张立栋,于丁一,刘朝青,等.不同离心率下椭圆形滚筒内二组元颗粒混合[J].武汉理工大学学报,2015,37(4):87-93.
[13] D.Li,G.Liu,H.Lu,et al.Numerical simulation of different flow regimes in a horizontal rotating ellipsoidal drum[J].Powder Technology,2016,291(6):86-96.
[14]李少华,王丽伟.回转炉内壁炉型结构对颗粒混合效果的影响[J].煤炭学报,2013,38(10):1878-1881.
[15]闫明,段文山,陈琼,等.不同形状混合器中二元颗粒的分聚与混合研究[J].力学学报,2016,48(1):64-75.
[16] N.Gui,J.Fan,J.Gao,et al.Particle mixing study in rotating wavy wall tumblers by discrete element method simulation[J].Industrial & Engineering Chemistry Research,2014,53(33):13087-13097.
[17]李少华,张立栋,张轩,等.回转式干馏炉内影响颗粒混合运动因素的数值分析[J].中国电机工程学报,2011,31(2):32-38.
[18] H.Henein,J.K.Brimacombe,A.P.Watkinson.Experimental study of transverse bed motion in rotary kilns[J].Metallurgical Transactions B,1983,14(2):191-205.
[19]冯俊小,林佳,李十中,等.秸秆固态发酵回转筒内颗粒混合状态离散元参数标定[J].农业机械学报,2015,46(3):208-213.
[20]欧阳鸿武,黄立华,王琼,等.转鼓中双组元颗粒混合物形成斑图的模式和机制[J].粉末冶金材料科学与工程,2014,19(1):15-23.
[21] P.M.C.Lacey.Developments in the theory of particle mixing[J].Journal of Applied Chemistry,1954,4(5):257-268.
[22]张立栋,朱明亮,李少华,等.回转干馏炉内二组元颗粒混合机理及混合度分析[J].化工进展,2011,30(11):2382-2387.

