空间负荷预测中确定元胞负荷最大值的经验模态分解方法

肖 白，房龙江，李介夫，綦雪松，白乙然

(1．东北电力大学电气工程学院，吉林吉林132012;2．国网吉林供电公司，吉林吉林132001)

空间负荷预测(Spatial Load Forecasting，SLF)是针对待测区域内负荷时空特性的预测［1～3］，其结果的准确性将直接影响到城市电网的电源布点、供电路径选择、设备投运等是否技术可行且经济合理［4］．

实现SLF的过程中，一般需要使用元胞的年负荷最大值［5］，但在使用通过数据采集系统(SCADA系统)获取到的元胞负荷数据时，由于受到测量、通信等误差的影响，测量得到的最大值数据存在与实际最大值明显不符的情况，如若直接将测量到的各元胞历史负荷原始数据的最大值应用于SLF，势必会影响到预测精度［6］．因此在负荷预测过程中，需要对测量的负荷数据进行数据预处理，确定出元胞负荷的合理最大值，以确保在建模和预测过程中所使用的最大值数据能够合理地反映元胞负荷发展的趋势和规律，从而提高 SLF 质量［7～9］．

常用的数据预处理方法主要包括:傅里叶变换、小波变换以及经验模态分解(Empirical Mode Decomposition，EMD)方法等［10～16］．文献［13］利用傅里叶变换对负荷时间序列进行分解得到日周期、周周期、高频以及低频分量，但非日、周的周期分量可能被划分至高频或低频分量中，可能导致对规律性的挖掘不够彻底;文献［14］应用小波的奇异性检测原理对负荷数据中的奇异数据进行处理，但最佳的小波基和分解尺度的确定存在困难．文献［15］运用EMD方法将负荷原始时间序列分解得到一系列本征模态函数(Intrinsic Mode Function，IMF)，尽管EMD方法与小波变换相比，具有不需要预先设定小波基和分解尺度，可根据信号自身的特征进行分解，具有自适应性，但是如何通过分解得到的IMF确定高频分量，还有待进一步的研究．

针对以上问题，本文提出了基于EMD方法的元胞负荷合理最大值的确定方法，通过建立能够表征元胞基本信息的规律性、趋势性的主体分量和刻画随机波动性的高频分量的滤取机制，剔除高频分量来抑制随机波动性带来的不利影响，从而将主体分量的最大值作为元胞负荷的合理最大值．实例分析证明运用该方法进行数据预处理后再进行预测，能够有效地提高SLF结果的精确度．

1 经验模态分解基本原理

EMD是一种对信号进行平稳化处理的过程，它基于信号的局部特征尺度，将任意信号中不同尺度的波动逐级分解出来，产生一系列不同特征尺度的数据序列，并将每个序列作为一个IMF［16～19］，最后一个又称为残余函数．IMF满足如下两个条件:

(1)对于整个数据序列集合，其存在的极值点和过零点在数量上必须相等或者至多相差一个;

(2)在任意时刻，由极大值点和极小值点定义的上、下包络线均值为零［18］．

经验模态分解过程如下:对任意信号p(t)，首先确定出p(t)上的所有极值点，然后将所有极大值点和所有极小值点分别用一条曲线连接起来，使两条曲线间包含所有的信号数据，将这两条曲线分别作为p(t)的上、下包络线．若上、下包络线的平均值记作m(t)，p(t)与m(t)的差记作h(t)，则

将h(t)视为新的p(t)，重复以上操作，直到当h(t)满足IMF条件时，记

c1(t)表示为一个IMF，再做

将r(t)视为新的p(t)，重复以上过程，依次得到第二个IMF、c2(t)，第三个IMF、c3(t)，等．当cn(t)或r(t)满足给定终止条件(分解出的IMF或残余函数r(t)足够小或r(t)成为单调函数)时过程终止，得分解式

式中:r(t)称为残余函数．

2 各分量滤取机制的建立

元胞负荷序列是一典型的具有周期性和随机性的非平稳时间序列［19］，其中具有随机波动性的负荷以高频分量的性质体现出来［13］．因此可以通过对负荷序列进行分解，解析出表征负荷随机波动性、规律性以及趋势性的数据序列，利用具有规律性以及趋势性的分量重构出负荷的主体分量，其余随机波动性较强的分量作为高频分量，从而实现对所需分量的滤取．

本文基于EMD方法的优势，采用EMD方法对元胞负荷序列进行分解．为了更清楚地看出元胞负荷及各IMF波形特点，这里仅以某元胞的14天历史负荷数据(采样间隔为5 min)为场景展开分析，该元胞的负荷序列以及分解得到的IMF与残余函数见图1(各IMF的单位为MW)，其中图1(a)为负荷序列，图1(b)至图1(l)为经验模态分解的结果．

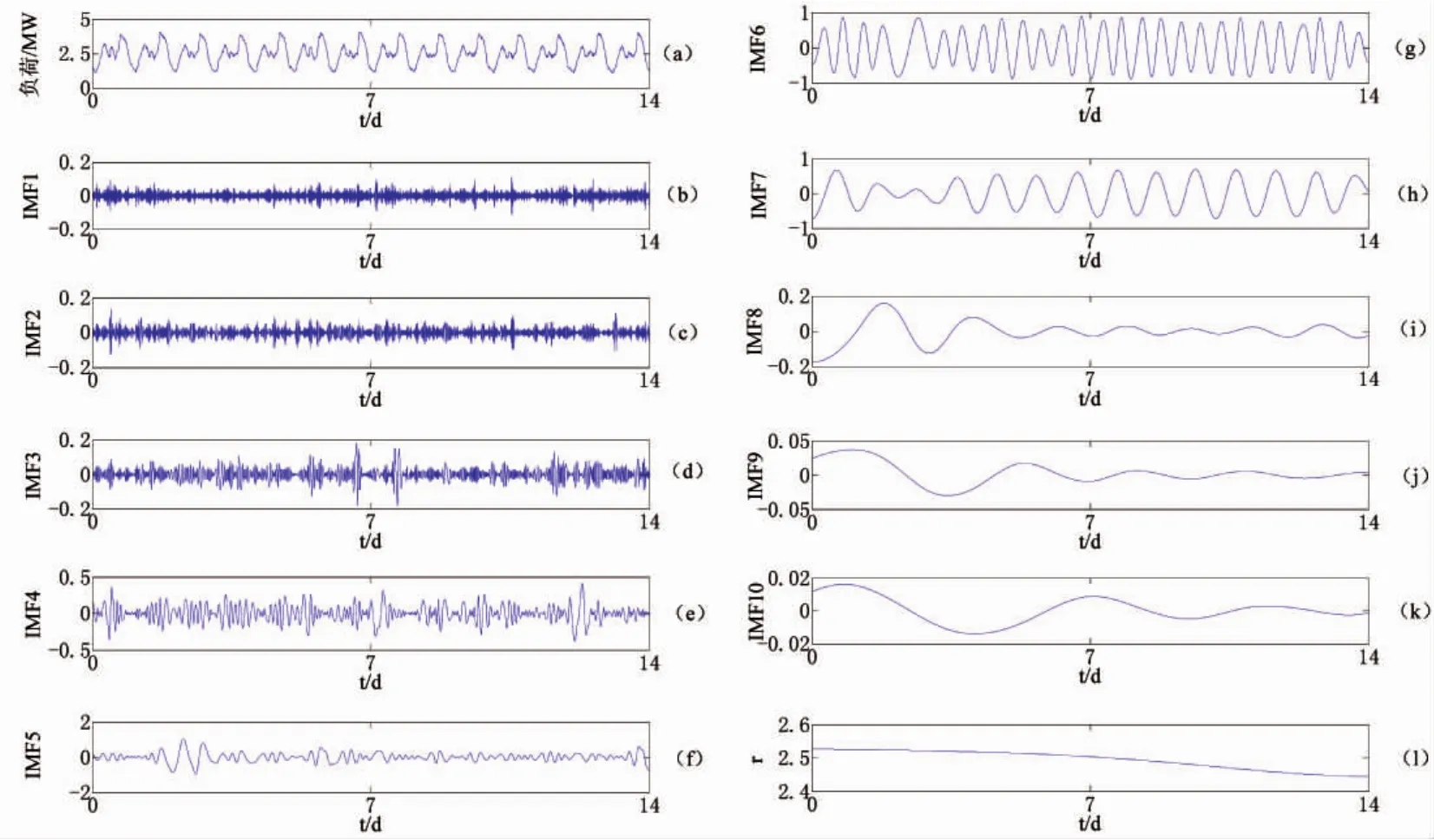
图1 负荷序列及经验模态分解

由图1可见，元胞的负荷序列经EMD得出的IMF与残余函数r(t)的波动程度依次由杂乱且剧烈波动到趋于平稳．为了定量描述其波动程度，本文引入了波动指数公式(5)进行描述．

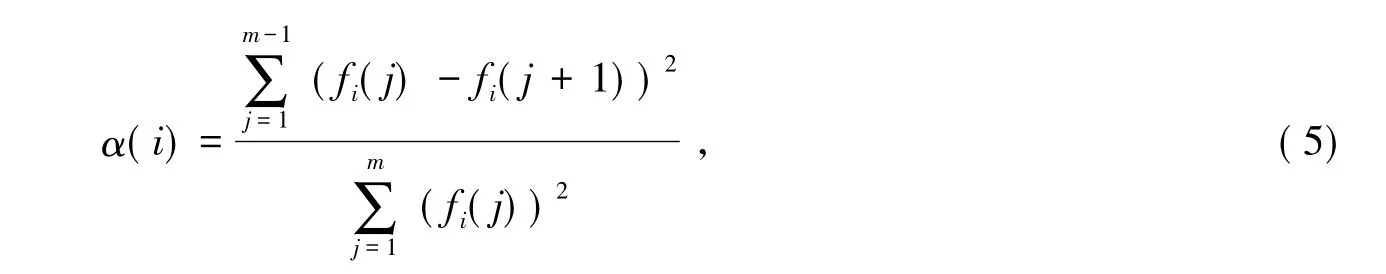
式中:α(i)为元胞负荷的第i个数据序列的波动指数，i=1，2，…，n;n为对元胞负荷进行经验模态分解所得到的数据序列的个数;fi(j)为第i个负荷数据序列的第j个负荷值，j=1，2，…，m;m为第i个负荷数据序列所含负荷值的个数．

通过公式(5)可分别计算出IMF1～IMF10、残余函数r(t)以及负荷序列p(t)的波动指数，如表1所示．

表1 各IMF、残余函数以及负荷序列的波动指数

由表1和图1可知，数据序列波动得越杂乱剧烈，其波动指数越大;越趋于平稳的数据序列，其波动指数越小．

如前文所述，元胞负荷共包含高频分量和主体分量两个部分，其中高频分量具有随机波动性，主体分量则具有规律性和趋势性．下面利用波动指数建立判据，来判定分别属于高频分量的IMF和主体分量的IMF．

(1)建立确定IMF属于高频分量的第一判据

“第一判据”的核心思想是高频分量的波动指数至少会高于元胞负荷原始数据序列的波动指数．通过比较元胞负荷的各IMF的波动指数与元胞负荷原始数据序列的波动指数之间的关系，把满足公式(6)的IMF初步判定为高频分量．

式中:α(0)为元胞负荷原始数据序列的波动指数．

根据公式(6)和表1，可初步判定所分析元胞负荷中的IMF1～IMF6属于其高频分量．

(2)建立确定IMF属于高频分量的第二判据

“第二判据”的核心思想是认为波动指数快速衰减前的IMF的高频特性更为明显．利用公式(7)求出各相邻两个IMF的波动指数的比值，在根据“第一判据”所得到的IMF中确定b(i)的最大值，并将该b(i)最大值对应的i记作k，判定第1至第k个IMF均属于高频分量．

式中:b(i)为波动比例序列的第i个值，i=1，2，…，n－1;α(i)为元胞负荷的第i个IMF的波动指数，i=1，2，…，n－1;n为对元胞负荷进行经验模态分解所得到IMF的个数．

根据表1中各IMF的波动指数，利用公式(7)生成波动比例序列，如图2所示．

根据表1和公式(7)，以及图2，可进一步判定IMF1～IMF3属于其高频分量．

综上所述，可以将滤取出来的IMF1～IMF3进行重构作为负荷序列的高频分量;利用IMF4～IMF10以及残余函数r(t)重构，得到负荷序列的主体分量．

图2 波动比例序列

3 基于EMD方法确定元胞负荷最大值

本文提出的基于EMD方法确定元胞负荷合理最大值的具体步骤如下:

(1)按照城市电网中每条10 kV馈线的供电区域来生成元胞;

(2)运用EMD方法将各元胞负荷时间序列分解为一系列的IMF和r(t);

(3)通过引入波动指数分别描述每个IMF和r(t)的波动程度，根据元胞负荷波动特性建立滤取机制;

(4)根据建立的滤取机制滤取出属于高频分量的IMF并予以剔除，利用其余的IMF与r(t)重构出主体分量;

(5)提取主体分量中的最大值作为元胞负荷合理最大值．

对图1中IMF1～IMF3重构所得的元胞负荷高频分量的波形，如图3所示．对图1中IMF4～IMF10以及r(t)进行重构所得的元胞负荷主体分量的波形，如图4所示，其最大值就是元胞负荷的合理最大值．

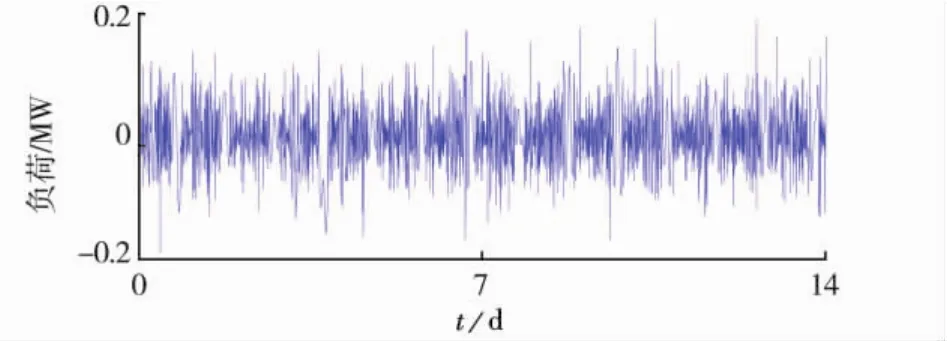
图3 高频分量

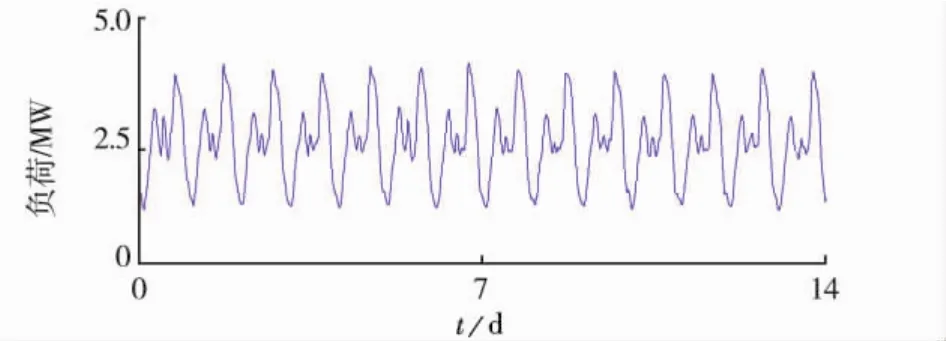
图4 主体分量

4 实例分析

以东北某城市中某一供电分局为例，该分局所辖28条10 kV馈线的各自供电范围，如图5所示［20］．按照28条馈线供电区域生成28个元胞．已知它们2004年至2008年的负荷历史数据(每5分钟一个采样点)，获取元胞的年负荷最大值(即一年为一个时点)．为叙述方便，将直接使用每年中最大负荷作为元胞负荷最大值进行预测的方法称为“直接预测”;将经过本文确定出元胞负荷最大值再进行预测的方法称为“经EMD方法预处理”．

通过数据采集系统得到的各元胞最大负荷值与基于EMD方法得到的最大负荷值，如表2所示．

图5 待预测区域中的元胞

表2 各元胞的年最大负荷值

在“直接预测”和“经EMD方法预处理”两种条件下，分别单独使用“灰色理论法”、“指数平滑法”、“线性回归法”预测2009年各元胞负荷最大值，预测结果，如表2所示．由于“北大线”和“西安线”在2009年的负荷实测值为0，故未在表3中给出．

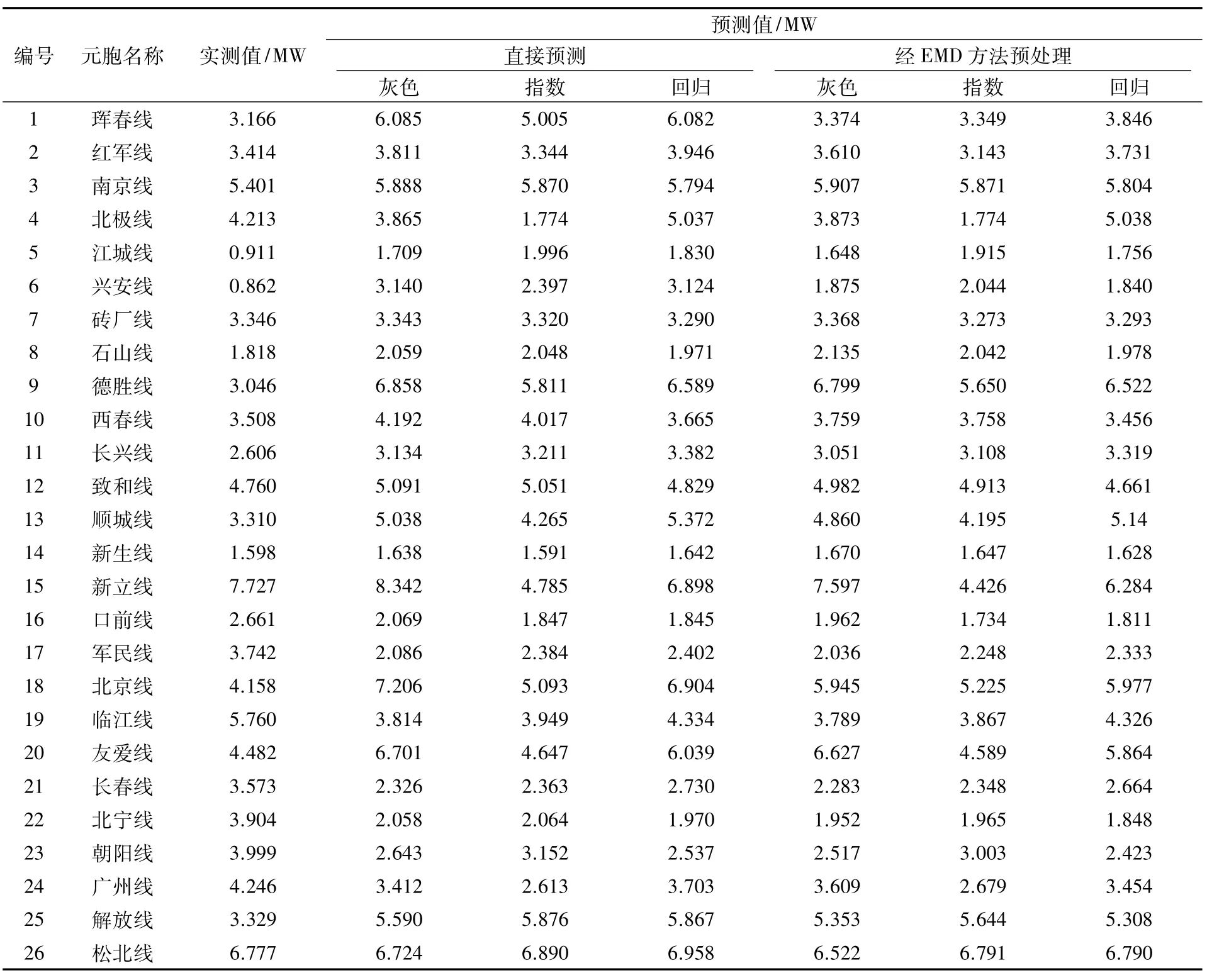
表3 各元胞的负荷预测结果

表3中各方法预测结果的总体预测误差，如表4所示．可以看出，“经EMD方法预处理”后的SLF误差均小于“直接预测”的SLF误差．

表4 元胞负荷的总体预测误差表

5 结 论

本文提出了一种基于EMD技术确定元胞负荷最大值的数据预处理方法，其优势与特色如下:

(1)运用EMD技术对元胞负荷进行分解，并引入了波动指数来定量刻画分解得到的各数据序列的波动程度．在分析元胞负荷特征的过程中，既能避免采用小波变换时所面临的如何确定小波基与分解层级的问题，也能避免采用傅里叶变换时所面临的如何重构来保证特征信息分量完整性的问题．

(2)构建了确定各IMF是否属于高频分量的组合式判据，形成了滤取高频分量和主体分量的机制．该组合式判据能够根据元胞负荷序列自身的特征，自动地找到高频分量和主体分量之间边界，具有自适应性，可以消除主观因素带来的影响．

(3)将主体分量的最大值作为元胞负荷最大值．该预处理后的元胞负荷最大值用于SLF时，能够克服原始元胞负荷数据在测量、采集、传输过程中受到某些不确定性因素影响而导致预测精度降低的问题．

［1］ 肖白，周潮，穆钢．空间电力负荷预测方法综述与展望［J］．中国电机工程学报，2013，33(25):78－92．

［2］ 乐欢，王主丁，肖栋柱，等．基于空区推论的空间负荷预测分类分区实用法［J］．电力系统自动化，2009，33(7):81－85．

［3］ 余贻鑫，张崇见，张弘鹏．空间电力负荷预测小区用地分析(一)［J］．电力系统自动化，2001，25(6):23－26．

［4］ 肖白，黎平．城网空间电力负荷预测中的负荷规律性分析［J］．电网技术，2009，33(20):113－119．

［5］ 肖白，徐潇，穆钢．空间负荷预测中确定元胞负荷最大值的概率谱方法［J］．电力系统自动化，2014，38(21):47－52．

［6］ 宋亚奇，周国亮，朱永利．智能电网大数据处理技术现状与挑战［J］．电网技术，2013，37(4):927－935．

［7］ 康重庆，夏清，张伯明．电力系统负荷预测研究综述与发展方向的探讨［J］．电力系统自动化，2004，28(17):1－11．

［8］ 毛李帆，姚建刚，金永顺，等．中长期负荷预测的异常数据辨识与缺失数据处理［J］．电网技术，2010，34(7):148－153．

［9］ 杨薛明，苑津莎，王剑锋，等．基于云理论的配电网空间负荷预测方法研究［J］．中国电机工程学报，2006，26(6):30－36．

［10］刘红柳，杨茂．基于小波变换和支持向量机的风电功率爬坡事件识别与预测［J］．东北电力大学学报，2017，35(3):44－49．

［11］李国庆，张钰，张明江，等．基于MRMR的集合经验模态分解和支持向量机的风电功率实时预测［J］．东北电力大学学报，2016，36(6):30－35．

［12］尚海昆，王坤，李峰．基于集合经验模态分解法的局部放电信号去噪［J］．东北电力大学学报，2016，36(4):32－38．

［13］穆钢，侯元凯，杨右虹，等．负荷预报中负荷规律性评价方法的研究［J］．中国电机工程学报，2001，12(10):97－102．

［14］高山，单渊达．小波奇异性检测在负荷数据纠错和平滑处理中的应用［J］．中国电机工程学报，2001，21(11):105－108．

［15］刘耀年，杨德友，庞松岭，等．基于经验模态分解与动态神经网络的短期负荷预测［J］．电工电能新技术，2008，27(3):13－17．

［16］叶林，刘鹏．基于经验模态分解和支持向量机的短期风电功率组合预测模型［J］．中国电机工程学报，2011，31(31):102－108．

［17］杨茂，陈郁林．基于EMD分解和集对分析的风电功率实时预测［J］．电工技术学报，2016，31(21):86－93．

［18］汤庆峰，刘念，张建华，等．基于EMD－KELM－EKF与参数优选的用户侧微电网短期负荷预测方法［J］．电网技术，2014，38(10):2691－2699．

［19］张金良，谭忠富．基于经验模态分解和计量经济学模型及混沌模型的短期负荷预测［J］．电网技术，2011，35(9):181－187．

［20］肖白，穆钢，黎平，等．空间负荷预测中的负荷时序消差方法［J］．电力系统自动化，2010，34(16):50－54．