基于粗糙集和决策熵评价模型的水利工程监理投标风险分析

胡 鑫

(辽宁省观音阁水库管理局有限责任公司，辽宁 本溪 117100)

随着水利工程监理单位的业务范围和专业水平的不断提高，工程招投标企业之间的竞争越来越激烈，而准确地对投标风险进行分析将直接影响到投标的中标率和利润的回报程度[1- 5]。对投标进行风险性分析和如何操作规避风险的研究相对较少，在实际的工程投标过程中，往往因缺乏较为全面的系统性分析，对实际的经验数据的探讨分析相对较浅，而在实际投标的过程中和操作行为中存在较大的主观性能。据此，本文依据粗糙集理论和决策熵理论，通过将二者进行有效的结合，构建了适用于监理投标风险性分析的评价模型，可有效对不确定性信息进行筛选，并能够定性和定量的对评价指标进行归一化处理计算，相对于其他风险性评价计算模型具有明显的特点和优势[6]。

1 粗糙集和决策熵评价模型

1.1 粗糙集理论及属性

设定R为属性集合，U为粗糙集理论域，C为条件属性，D为决策属性，则决策表为S=，其中C∪D=R，C∩D=φ；假设Va为a属性的值域，则信用函数f:U×R→V，具体的意义表示任意对象x的属性值；P⊆R属性值所对应的一个二元不可区分关系如下所示：

IND(P)={(x，y)∈U×U

(1)

|f(x，a)=f(y，a)，∀a∈P}

(2)

式中，IND(P)—U/IND(P)即U的一个划分，简记U/P；且在U/P中的任意一元素[x]p可用下式进行表述，且下述公式被称为[x]p的等价类元素。

[x]p={y|f(x，a)=f(y，a)，∀a∈P}

(3)

X的P下近似值可定义为对于任意子集x∈U，任意属性集合P，Q⊆R，有P(X)=∪{[x]p|[x]p⊆X}，并且称Posp(Q)=∪{P(X)|X∈U/Q}为Q的P正域。一致决策表可表达为Posc(D)=U，其他情形则为不一致决策表；设定一致对象集为Posc(D)中元素，则不一致对象集为U-Posc(D)中的元素；若在不一定对象集用D0=U-Posc(D)表示，则D0=CD0，故在S的一致决策表中有CD0=φ。

r为P中Q的不必要条件可表述为对于任意的r∈P，Posp(Q)=Pos(P-r)(Q)，相反则r为P中Q的必要条件；P为Q的对立可表述为P中任意r都为Q的必要条件；设定S⊆P，则成为S为P的约简。由P中所有Q必要的原始关系条件的构成即为P为Q的核可表述为当且仅当S是P的独立子族，并且满足Poss(Q)=Posp(Q)时，P中所有的Q的原始的构成要素的集合并可标记为CoreQ(P)。

1.2 熵理论及决策熵

熵值理论体系在任意一属性集合中有A在粗糙集理论域U所导出的划分为U/A={A1，A2，…，Am}，则集合A的熵可采用下式进行计算：

(3)

式中，pi—Ai在粗糙理论域U上的概率，pi=|Ai|/|U|；对于决策表S=C∪D=R，C∩D=φ中的P和D，P⊆C且在U上可进行如下的导出划分：

U/P={X1，X2，…，Xn};U/D={D1，D2，…，Dt}

(4)

对于U∪D的属性集合的熵可按下式进行计算：

(5)

式中，|Xi∩Dj|/|U|—在某决策规则下的对象覆盖度，决策熵值的大小是决策表中表征决策能力变化的的重要参数指标。

P在决策属性集D中的粗糙熵可按下式进行计算：

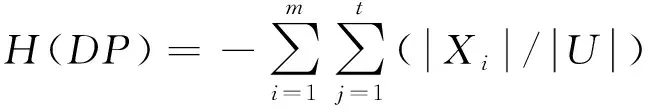
(6)

当决策表S=存在不一致的情况时，可对C在U上所导出的划分为U/D，将其进行等价类逐步细化和分析所得到的等价关系标记为RD，且可用下式进行表述：

U/RD={CD0，CD1，CD2，…，CDt}

(7)

同时可得P在RD上的决策熵，如下所示：

H(RD/P)=H(RDP)+H(P∪RD)

(8)

条件属性集B⊆C时，则对于任意属性a∈C-B在决策表S=中的属性重要性计算可按下式进行表述：

SGF(a，B，D)=H(RD|B)-H(RD|B∪a)

(9)

当属性集B为空集是，则有：

SGF(a，φ，D)=-H(RD|∪a)

(10)

式中，SGF(a，B，D)—此值的大小表示在已知条件B的作用下，属性a对于指标B的重要性程度。

对于D在C中B的一个约简的充分必要条件如下：

H(RD|B)≤H(RD|C)

(11)

对于任意的属性b∈B时，有以下条件：

H(RD)|(B-b)>H(RD|C)

(12)

2 实际工程应用及结果分析

2.1 样本的选取

本文以我国北方某水利工程监理公司在2012～2015年的监理投标为研究背景，对该公司在18次投标中存在多种风险因素进行识别和分析，并从中选取具有一定代表性的15项风险投标信息为研究样本[7]。

2.2 投标风险要素

监理工程的投标活动一方面受自身的独立特性的影响显著，另一方面与建设主体的其他构筑物密切相关，故在投标过程的风险性分析进行存在较大的困难。不仅要考虑到投标项目的全面性，而且还应与客观实际情况相结合[8]。据此，本文根据水利工程的建设特点和监理单位的经验和业务能力，选取了在监理目标管理过程中影响较为明显的15项风险要素进行识别和分析。本研究所选取的投标风险要素主要包括不可抗力因素作用C1、恶劣气候环境C2、洪水灾害C3、区域市场经济现状C4、国家相关制度政策C5、政府的人为干预C6、业主的资金落实情况C7、业务与施工单位的关系C8、业主管理人员能力C9、公司运营状况和预期目标C10、公司自身能力现状C11、公司与业主的管理C12、各竞争方的实例和竞争数量C13、竞争方投标的积极性C14、施工单位的施工能力C15。

2.3 信息离散化处理

本文在查阅相关文献资料并考虑有关专家学者经验的基础上[9]，结合水利工程投标的实际状况，分别将不同的投标风险要素按照两个等级进行划分评价，即评价结果为好或不好，所对应的评价值分别为1和2。监理投标风险的定性分析结合相关专家的评价值进行量化处理，监理公司在18次投标过程中的各投标风险要素的评价结果见表1。

2.4 求解过程

首先进行Posc(D)和D0=U-Posc(D)的计算，并得到U/(RD)的计算结果；依次按照文中所述公式进行CoreD(C)和H(RD|C)的计算，然后另B=CoreD(C)，当B为空集时，直接进行SGF(a，B，D)的计算，当H(RD|B)≤H(RD|C)进行决策表S的相对约简计算；对于任意影响因子a∈C-B，则可以进行H(RD|(B∪a))和SGF(a，B，D)的计算；当a同时满足多个属性时，则对于SGF(a，B，D)的最大属性值进行选取并标记为a，同时该属性值还应满足与其相对应的等价类数的最大即当B=B∪a时，有|U/(B∪a)|的最大；当H(RD|B)>H(RD|C)时，则返回上述计算，重新进行判别，否则进行B=B-CoreD(C)的计算，且计算过程应满足决策熵基本约束条件和权重系数的计算；最终可得决策表S所对应的相对简约集合B，计算结束。

2.5 工程应用

本文利用文中所述计算过程和基本公式，并结合监理公司所选取的样本信息，通过将表1和表2的数据输入建立投标风险识别计算模型可得决策表S=，粗糙集理论域U={x1，x2，…，x18}；条件属性集有C={c1，c2，…，c15}；决策属性有D={d1，d2}。根据监理工程的实际情况，并按照计算公式可得：

PosC(D)={x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11，x12，x13，x14，x15，x16，x17，x18}

D0=U-PosC(D)={x3，x9，x14}，{x1，x2，x4，x5，x6，x7}，{x8，x10，x11，x12，x13，x15，x16，x17，x18}

CoreD(C)={c1，c7，c8，c10，c12，c13，c14，c15}

H(RD|C)=3.617，H(RD|B)=4.282

C-B={c2，c3，c4，c5，c6，c9，c11，c14，c15}

按照上述计算公式分别可进行H(RD|(B∪ai))，a∈(C-B)和SGF(a，B，D)，本研究所选取的各投标风险要素计算结果见表2。

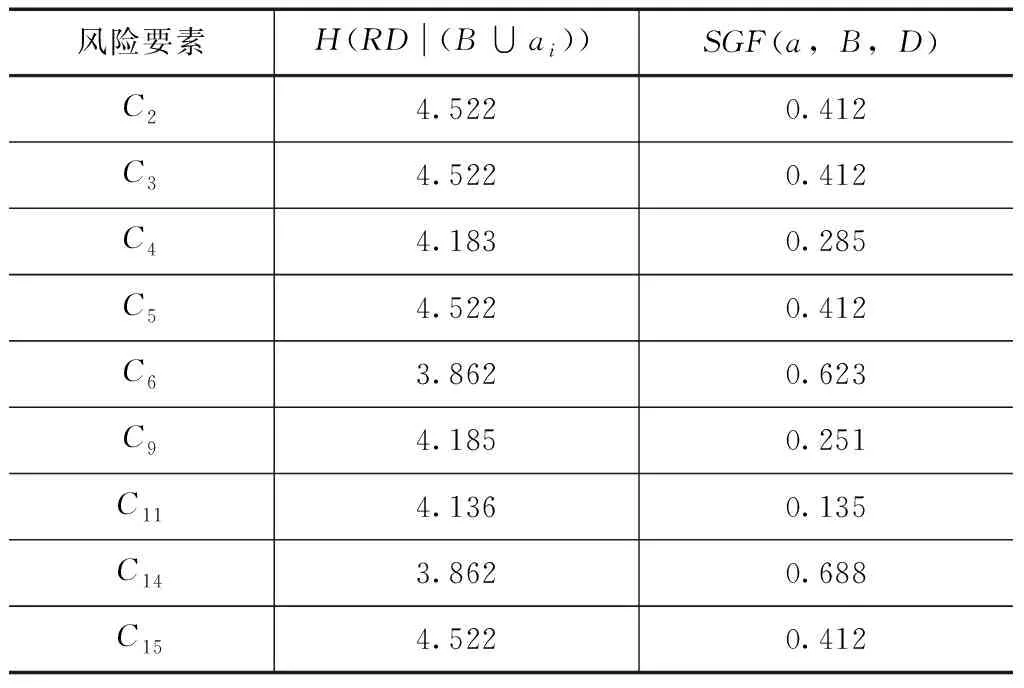
表2 监理投标风险要素简约计算结果表

利用文中所述计算公式可知C6和C14计算结果均满足计算条件要求，并经过计算验证，最终可得最小相对属性约简B如下：

P1={c1，c7，c8，c10，c12，c13，c14，c15}

P2={c1，c7，c8，c10，c12，c13，c14，c15}

2.6 结果分析

根据上述计算结果可知，影响监理公司的投标风险的关键性因素主要包括不可抗力因素作用C1、业主的资金落实情况C7、业务与施工单位的关系C8、业主管理人员能力C9以及施工单位的施工能力C15；而国家相关制度政策C5、政府的人为干预C6、国家相关制度政策C5、政府的人为干预C6是影响水利工程监理投标的一般性风险因素；其他各因素对监理的投标风险影响较少，故在之后的水利工程投标活动中应充分考虑并进行识别分析关键性和一般性风险因素[10- 11]。

3 结语

本文依据粗糙集理论和决策熵理论，通过将二者进行有效的结合，构建了适用于监理投标风险性分析的评价模型，可有效对不确定性信息进行筛选，并能够定性和定量的对评价指标进行归一化处理计算，得出的主要结论如下：

(1)影响监理公司的投标风险的关键性因素主要包括不可抗力因素作用C1、业主的资金落实情况C7、业务与施工单位的关系C8、业主管理人员能力C9以及施工单位的施工能力C15。(2)本文所建立的评价模型能够对监理风险要素进行近似的分类求解，其推理过程和计算公式有效的避免了不重要决策属性的冗余信息，能够较为准确、全面、客观的对投标风险进行识别、分析和预测，通过实例验证，本文的研究成果和计算方法可为监理公司在水利工程投标风险识别和方案决策分析中提供一定的理论支撑和参考依据。

[1] 刘兆国. 水利工程监理工作浅析[J]. 水利规划与设计, 2016(07): 86- 87．

[2] 汪达, 汪丹. 亭子口水利枢纽工程环保监理细则编制与实施[J]. 水力发电, 2014(09): 15- 16+28．

[3] 袁雪莲. 水利工程建设中监理工程师的作用与责任[J]. 水利规划与设计, 2014(06): 74- 75．

[4] 蔡德昌. 浅析建设工程项目中项目管理与工程监理合同服务范围与管理职责[J]. 水利水电技术, 2013(08): 102- 104．

[5] 王淑伟, 马宇. 浅析水利工程建设监理现状及对策[J]. 水利技术监督, 2015(06): 29- 30+38．

[6] 姚登友. 三里坪水利枢纽工程监理合同管理探讨[J]. 人民长江, 2012(06): 11- 13．

[7] 张宗超. 项目绩效评价模型在水利工程项目监理中的应用[J]. 水利技术监督, 2013(06): 19- 20．

[8] 聂相田, 郜军艳. 水利工程建设现场监理人员配置标准及验证[J]. 水电能源科学, 2012(08): 112- 115．

[9] 章皖东. 浅谈监理工程师对水利工程项目投资的控制[J]. 水利科技, 2012(04): 117- 118．

[10] 刘伟, 谢忱. 水利工程监理投资控制探析[J]. 质量, 2011(04): 27- 29．

[11] 刘仲池. 水利工程监理中的“三控制”研究[J]. 河南水利与南水北调, 2015(06): 43- 44．