多策略人工蜂群算法在梯级水库优化调度中的应用

徐弘达

(凌源市水务局，辽宁 朝阳 122500)

近年来，我国的水利事业得到了持续的发展和提升。对于水库的调度问题已经由单一型的独立调度转向梯度水库群的联合优化调度，从而使水利的发展迈向了更加高效、便捷的快车道上。目前，国内外对梯度水库群的优化研究已取得了显著的成果，明波等[1]在水库调度优化理论的基础上，对一种线性的组合模型进行了动态规划和模拟，应用到具体的实例中，为该类水库优化调度问题提供了一种新的方法。万芳等[2]创建了一种简便的数学模型，该模型主要解决的是在水库优化调度中不能对反馈及协调向量这两者的平衡问题[3]。不过，随着水库数量的增加，梯级水库群优化调度的系统问题变得越来越复杂，传统的算法已经难以解决实际的应用，迫切需要更加智能化的算法来解决[4- 6]。在这样复杂问题的情况下，本文采用经过改进的多策略人工蜂群算法来对具体的梯级水库群的优化调度问题进行探析及解决，在求解精度和速度上满足实际需要，这对于缓解能源紧张的现状具有十分显著的意义。

1 实验及方法

1.1 改进狭义中心的人工蜂群算法(ISC-ABC)

狭义中心的形成源于群体所处的核心位置，通常比处于整体中最佳位置更易达到最优解，其中该中心的表达式为：

(1)

式中，FN—蜂群中蜜源的数量；C—改进狭义中心的位置。

在ISC-ABC的算法中，观察蜂和雇佣蜂应该采用进化的策略，来提高其算法的收敛速率，并对蜂群进入局部最佳的可能性降到最低程度。

1.2 综合学习的人工蜂群算法(CL-ABC)

为了解决算法整体功能不高，搜索能力不平衡的问题，拟构造一种综合学习的人工蜂群算法。该算法需要构造虚拟蜜源。其中，有两种构造方式为：

Ti，j=(Xk，j*FITk+Xi，j*FITi)/(FITk+FITi)

(2)

Ti，j=(Xl，j*FITl+Xk，j*FITk)/(FITl+FITk)

(3)

式中，Xk、Xl—不同的邻域蜜源；Ti，j—构造的虚拟蜜源。

同时，又创新了一种雇佣蜂的搜索方式：

Vi，j=(Gbestj-Ti，j)*+(Ti，j-Xm，j)*φ+Ti，j

(4)

式中，Xm—随机的邻域蜜源；φ—[0，1]区间的数值；φ—[-1，1]之间的数值。

这种新的搜索模式不仅对算法的收敛精度得到了提高，也促使种群具有一定的多样性[4]。

1.3 多策略人工蜂群算法(IMS-ABC)

在人工蜂群的算法中，源位置可以分为个体、邻域以及当前全局最优的蜜源，按照此分类，可以得到基本的搜索策略。在IMS-ABC算法中，扩展和改进了3种基本的搜索策略。根据算法的不同时期自适应调整，促进算法的搜索能力达到平衡[5]。于是，在目前整体最优的位置策略下进行改进，具体的公式为：

Vi，j=Gj+φ(Xi，j-Xk，j)

(5)

式中，Gj—目前整体最优的蜜源位置信息；φ∈(-1，1)之间的随机数值。

在每个个体自身的位置策略下进行改进，具体的公式如下：

Vi，j=Xi，j+φ(Xi，j-Xk，j)

(6)

式中，φ∈(-1，1)之间的随机数值。

1.4 梯级水库优化调度数学模型

为了解决越来越复杂的梯级水库优化调度问题，拟将改进的人工蜂群算法应用于该类问题的研究中，最重要的就是需要建立梯级水库优化调度的数学模型，该模型的建立需要选取决策变量，以水库每个月末的水位为基准，计算出在约束条件下的数值，并且以梯级水库群中总的发电量为目标函数即可。

其中，约束条件主要有以下几种，其一，对于水库水位的约束，具体为：ZLi，t≤Zi，t≤ZUi，t。其中，ZUi，t为在t时间段内第i个水库的最高约束水位值；ZLi，t为在t时间段内第i个水库的死水位。其二，对于水库的泄洪量约束条件为：QLi，t≤Qi，t≤QUi，t。QUi，t和QLi，t分别代表着在t时间段内第i个水库泄洪量的上下限。其三，水电站的出力约束条件为：NLi，t≤Ni，t≤NUi，t，NUi，t为装机容量；NLi，t为在t时间段内第i个水库的出力情况。对于目标函数而言，以梯级水库群中总的发电量为主来建立具体的调度模型。即:

(7)

Ni，t=ηi·Hi，t·Qi，t

(8)

式中，Δt—具体的时间段；E—总的发电量；ηi—发电机的整体出力指数；Hi，t—第i个电站在t时间段内的发电水头；Ni，t—第i个电站在t时间段内的出力；N、T—发电站的编码及调度时期的时间总量。

1.5 浑江流域水库的实验模拟

本文选取辽宁浑江流域水库中的3个水电站为主要研究对象，分别为：恒仁水电站回龙山水电站和太平哨水电站。当年发电量为12.6亿kW·h，水电站总的装机容量为52.3万kW。3座水电站的具体物性参数指标见下表1。

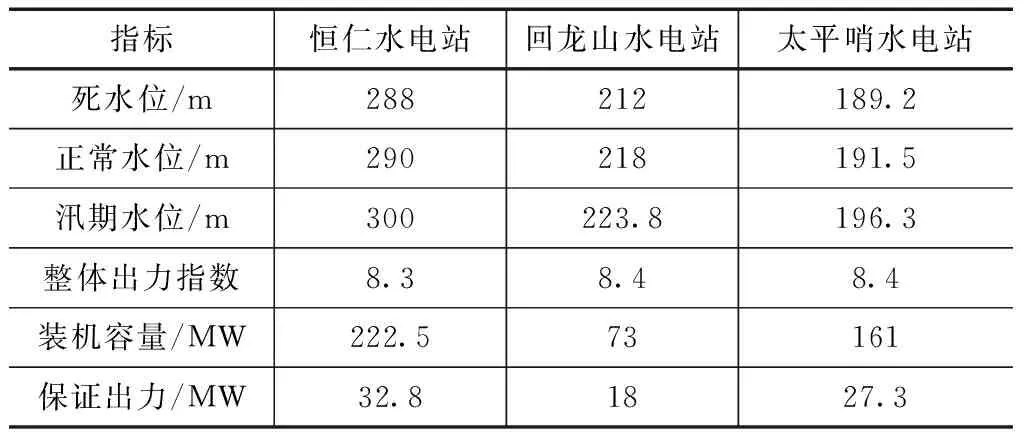
表1 3座水电站的具体物性参数指标

2 试验结果与分析

2.1 算法流程指导

分别选取ISC-ABC、CL-ABC以及IMS-ABC三种改进算法和MFABC、MABC、QABC、ABC四种传统算法对所建立的梯级水库优化调度的数学模型进行方程求解，并对结果进行对比优化参数。其中，必须对参数进行统一的初始化处理，即蜜源的数量为50，最大的迭代次数为105，种群数量为100，解的维数S=30，同时还要对模型中的约束条件进行确定[6]。

具体的流程为：开始先对种群进行初始化设置，再通过对流量、水库容量、出力等中间变量进行计算，并得出适应值，然后对目前种群的最佳信息进行更新，根据算法搜索过程寻找最佳的水位量，若有终止条件，则需要输出每个水库的总电量以及各时段的最优水位等，直到结束。

2.2 梯级水库优化调度的实验测试及分析

利用7种不同的算法对建立的梯级水库优化调度数学模型进行测试，其计算的总电量及运行时间结果具体见表2。

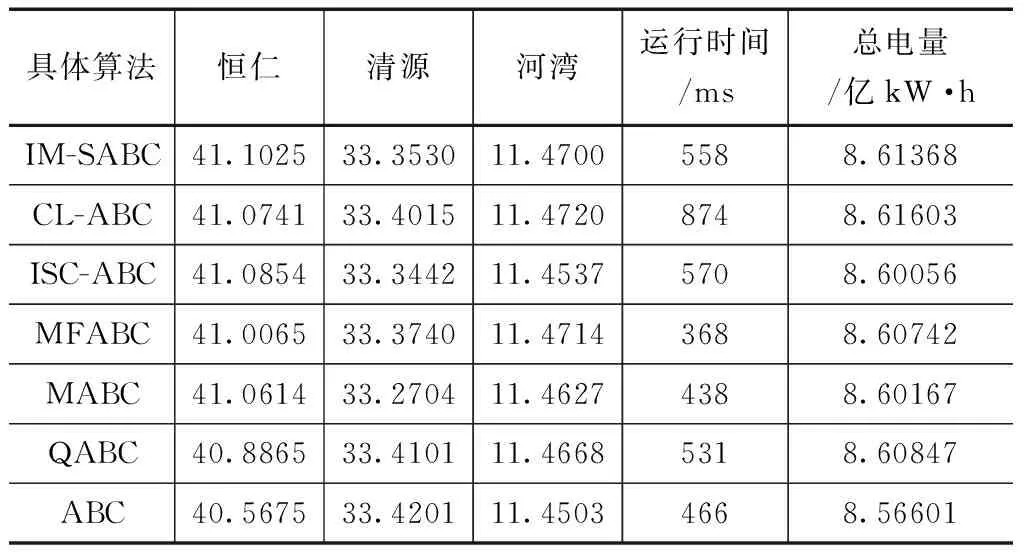
表2 不同算法计算出的电量结果

从表2中可以看出，采用改进的智能算法对梯级水库进行优化调度后的总电量和目前3座水电站的年发电量8.05亿kW·h相比，具有较好的改善效果，提高了产能。并且在一致的约束条件下，经过改进的ISC-ABC、CL-ABC以及IMS-ABC三种算法与传统的MFABC、MABC、QABC、ABC算法相比，能够获得更好的效果，其中采用CL-ABC算法进行测试的总电量为8.61603亿kW·h，这在7种算法中是最高的。并且在整个梯级水库的计算中，总发电量最大的算法为CL-ABC，其余的依次为IMS-ABC、ISC-ABC、MFABC、QABC、MABC和ABC算法。同时，在对每个算法运行的时间中可以得知，采用CL-ABC算法运行的时间比其他算法要高之外，IMS-ABC算法和ISC-ABC算法的运行时间和其余的算法相比没有很大的差别。

为了更好的对算法性能的优劣进行评价，其中，求解的速率是比较重要的一个因素，快速的求解在复杂的水库优化调度问题中能够为及时的调度优化提供很好的支持，图1为7种不同算法计算的总电量与测试次数的关系。

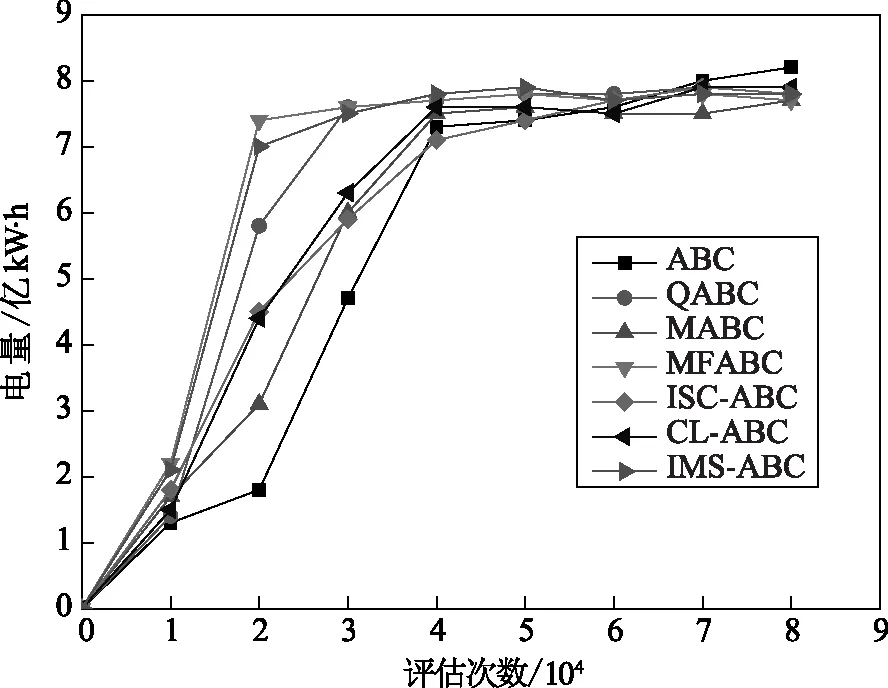
图1 不同算法计算出的电量随评估次数的变化曲线

从图1可以看出，采用ISC-ABC改进算法进行测试的结果曲线随着评估次数的增加上升趋势比较平缓，没有很大的变化，在一定程度上说明了水库的水位变化波动比较小，在实际的事例中有较好的应用。对于IMS-ABC算法而言，在初期有着较快的收敛速率，并且能够快速的找到最优解。综合而言，经过改进的3种人工蜂群算法在该水库的实际应用中都取得了较好的效果。

对于每一个水电站的水位变化情况的了解也是必须的，图2～4分别为恒仁水电站、回龙山水电站和太平哨水电站的水位变化曲线。

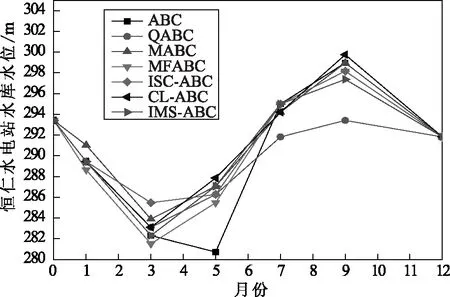
图2 恒仁水电站的水位变化曲线

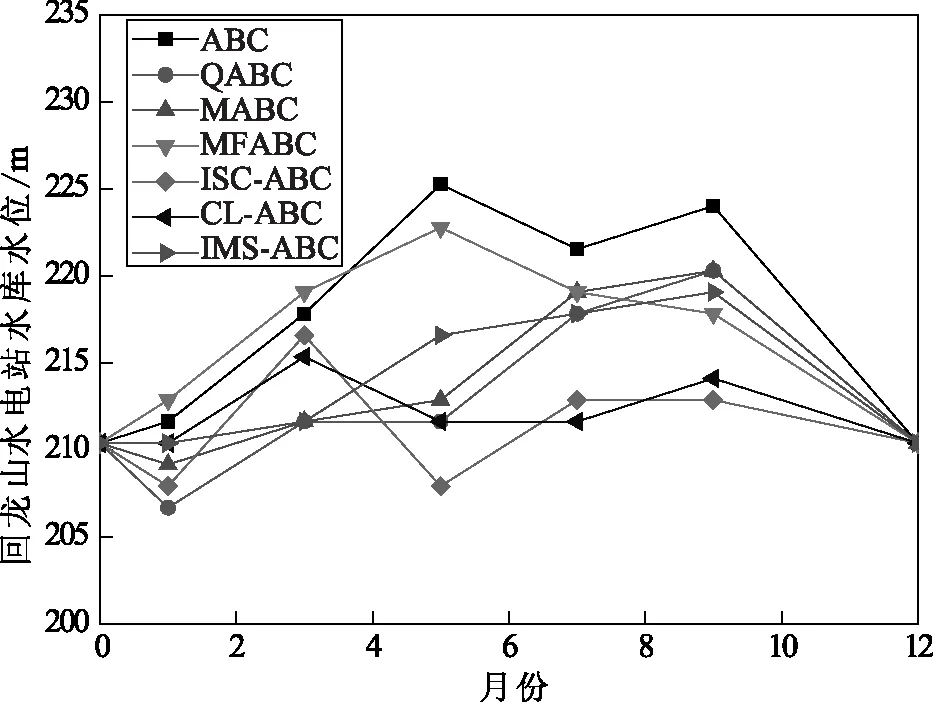
图3 回龙山水电站的水位变化曲线

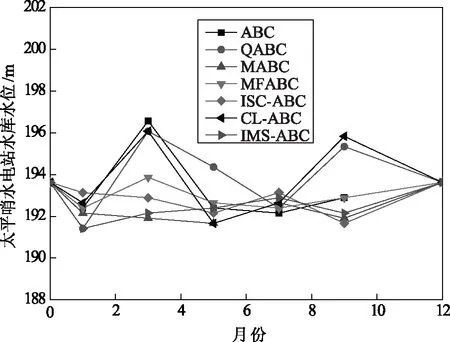
图4 太平哨水电站水位的变化曲线

从图2～4可以看出，采用改进的3种人工蜂群算法与传统的其他算法相比，由图2可知，每一种算法得出的水位变化曲线都呈现波浪型，整体的走势还是比较平缓的，对水库的调度是比较有利的，同时，尤其是ISC-ABC算法的测试结果最佳，能够充分的发挥出水库的蓄水功能。由图3可知，每一种算法得出的水位变化曲线波动性较大，不过对于CL-ABC算法而言，相比较于其他算法的测试结果还是最为平缓的，没有特别明显的波动。在图4中的太平哨水电站水库水位变化曲线中，每一种算法得出的水位变化曲线并没有呈现出明显的规律。总体而言，采用经过改进的3种算法—IMS-ABC、CL-ABC和ISC-ABC得到的测试结果表明，在这3种算法的测试下水库水位的变化曲线有着较小的波动，对浑江流域水库的梯级水库群优化调度的实际应用还是比较适用的。

在水电站的运行过程中，难免会出现水库中水量的浪费，其中弃水量能够反映出水能资源的综合利用情况，所以可以通过采用不同的算法对水能资源的利用进行对比。表3为采用7种不同的算法对梯级水库群优化调度后3个水电站的平均弃水量数据变化量。

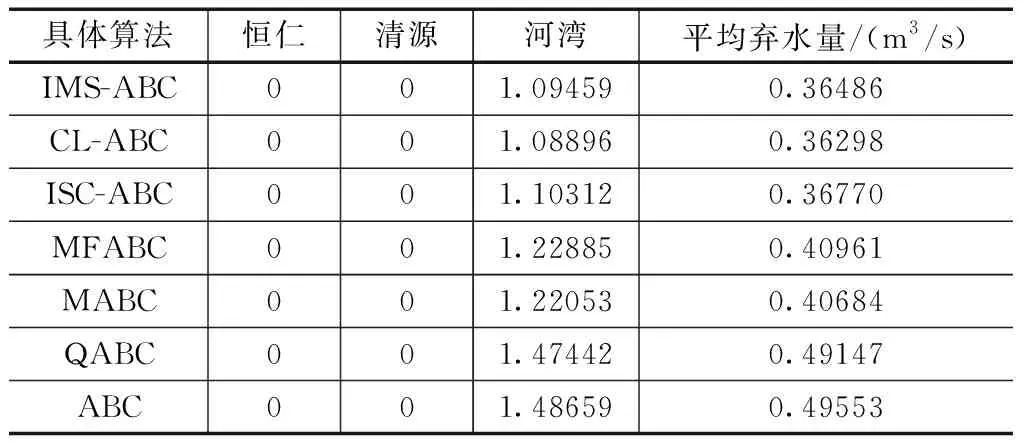
表3 不同算法计算出的平均弃水量对比结果

从表3可以看出，采用7种不同算法对恒仁水电站和回龙山水电站的弃水量测试结果均为0，至于对太平哨水电站的弃水量经过对比可知，经过改进的3种人工蜂群算法对水库的弃水量起到了明显的减少作用，并且实现了水资源综合利用的最大化。

3 结语

采用改进的3种人工蜂群算法来应用到浑江流域水库中的3个水电站中，经过实验测试结果表明，采用CL-ABC算法得出的总发电量最大，并且在每个水电站的水库水位随着月份的变化过程中，采用这3种算法对水库水位的变化曲线进行测试时存在较小的波动，对该流域梯级水库群优化调度的实际应用还是比较适用的。CL-ABC算法在求解精度和速度上满足实际需要，这对于缓解能源紧张的现状具有十分显著的意义。

[1] 明波, 黄强, 王义民, 等. 基于改进布谷鸟算法的梯级水库优化调度研究[J]. 水利学报, 2015, 46(03): 341- 349.

[2] 万芳, 原文林, 黄强, 等. 基于免疫进化算法的粒子群算法在梯级水库优化调度中的应用[J]. 水力发电学报, 2010, 29(01): 202- 206+212.

[3] 王欢. 水库运行管理及调度的有效方法分析[J]. 水利规划与设计, 2014(09): 55- 56+76.

[4] 刘克琳, 王宗志, 程亮, 等. 水库防洪错峰调度风险分析方法及应用[J〗. 华北水利水电大学学报(自然科学版), 2016, 37(06): 43- 48.

[5] 喻金平, 郑杰, 梅宏标. 基于改进人工蜂群算法的K均值聚类算法[J]. 计算机应用, 2014, 34(04): 1065- 1069+1088.

[6] 都兴朔. 结合人工蜂群算法的调和K均值聚类算法的研究[D]. 东北师范大学, 2012.

[7] 贾瑞红. 单一水库优化调度方案在水库调度中的应用研究[J]. 水利规划与设计, 2013(11): 23- 25.

[8] 郑慧涛, 梅亚东, 胡挺, 等. 改进差分进化算法在梯级水库优化调度中的应用[J]. 武汉大学学报(工学版), 2013, 46(01): 57- 61.

[9] 叶碎高, 温进化, 王士武. 多目标免疫遗传算法在梯级水库优化调度中的应用研究[J]. 南水北调与水利科技, 2011, 9(01): 64- 67.

[10] 胡晓松. 基于APSO-BP算法的水库生态优化调度研究[J]. 水利技术监督, 2017, 25(01): 112- 114+133.

[11] 贾瑞红. 水库在防洪作业中实现水资源防洪系统的最优调度[J]. 水利技术监督, 2013, 21(06): 13- 15.