基于实数信号的多相FFT实现
丁兆贵,张生凤,李宏圆
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引 言
传统快速傅里叶变换(FFT)借助多相结构[1]实现多相FFT,相比传统的FFT实现,多相结构降低了数据传输速率。一方面,实际应用中模数转换(ADC)信号为实数信号,FFT频谱呈现共轭对称特性,仅一半频域信息有效,这说明频域变换有一部分运算是冗余的;另一方面,传统多相FFT各通道互相耦合,需要同时输出,难以采用分治法将功能模块划分为不同的子模块。
基于传统多相FFT的特性,本文提出改进的多相FFT实现思路,改进后的结构仅提取一半频域信息,且改进后的奇偶信道可分别独立处理,即奇偶信道分治。本文主要分为4个部分:(1)对传统的理论模型进行介绍;(2)论述本文思路以及创新点;(3)针对不同算法进行仿真分析;(4)全文总结。
1 传统多相FFT结构
频域处理在侦察接收机中具有广泛的应用场景:信噪比提升、频率特性分析、宽带信道化等等。对于实时的ADC信号,借助多相结构可以实现变速率传输,降低对硬件运算速度的要求。
1.1 多相分解
设系统的系统函数为H(z),其定义为:
(1)
定义第m个多相分量为:
(2)
则H(z)可表示为:
(3)
对应结构[2]可表示为图1。

图1 多相滤波结构
1.2 多相FFT
假设x(n)长度为N(MxP),对应傅里叶变换:
(4)
令k=s+tP,借助多相结构表达,得出多相傅里叶变换:
(5)
进一步化简可得:
(6)
多相FFT结构可表示为图2。
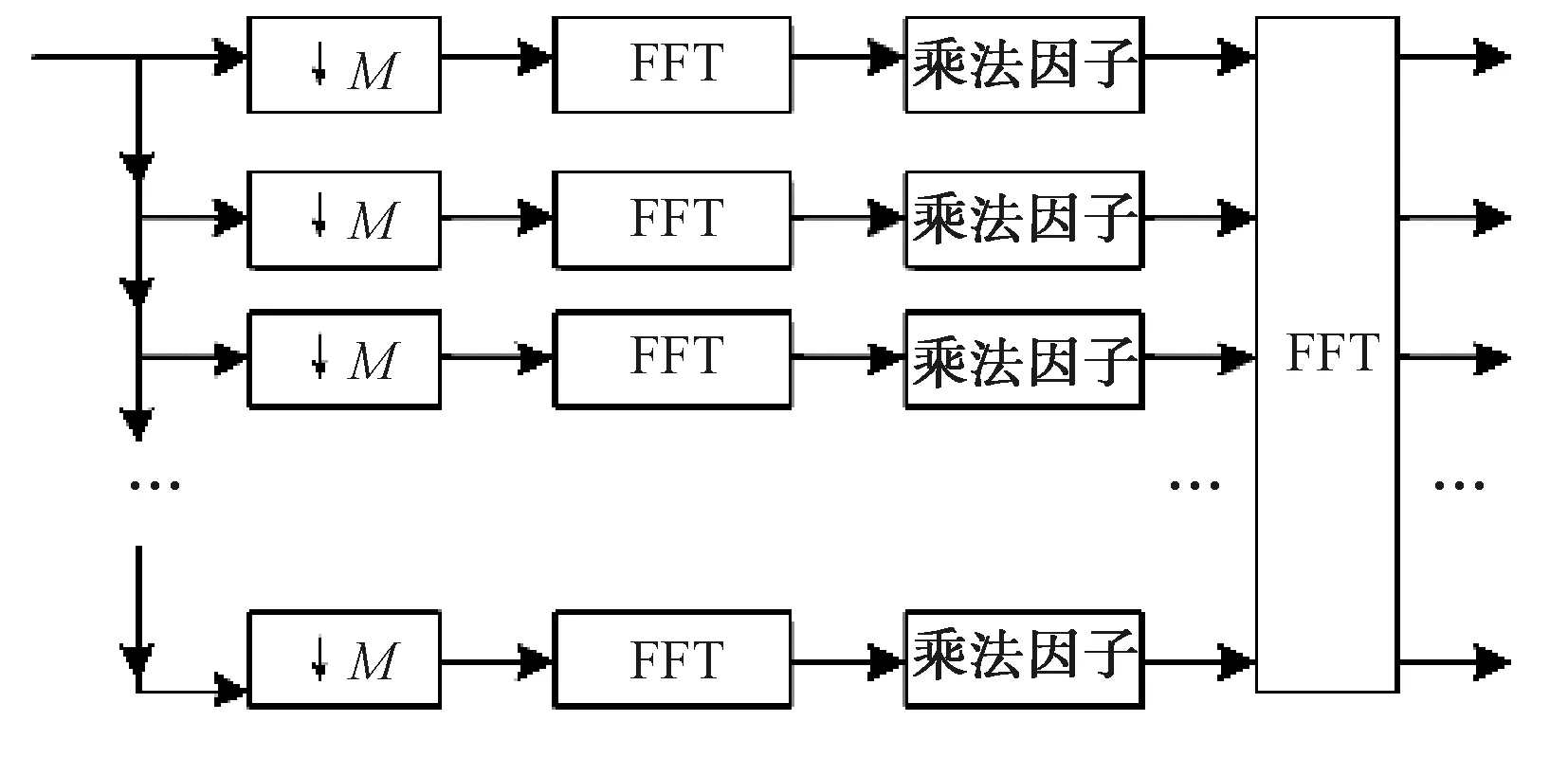
图2 多相FFT结构
2 改进的多相FFT
ADC采样信号为实信号,频域仅一半信息有效,从该点特性出发通过改进多相FFT结构,设计一种新的多相FFT实现结构。
2.1 改进思路
傅里叶变换体现了信号与各频率基信号的相关性,仅考虑频域一半信息的傅里叶变换:
k=0,1,…,N/2-1
(7)
式中:xeven为偶数序列;xodd为奇数序列。
通过该变换可得出结论:对于2N点数的单边谱,可通过2个N点FFT变换得到。
2.2 改进的多相结构
对于长度为N的序列x(n),DFT变换的频点可任意设定,假设N点序列DFT变换后频点个数为2N,给出单边谱(N点)结构的多相FFT表达式:
(8)
当t为奇数:
(9)
式中:DFT′[.]表示单边谱变换,即:
(10)
同样地,当t为偶数:
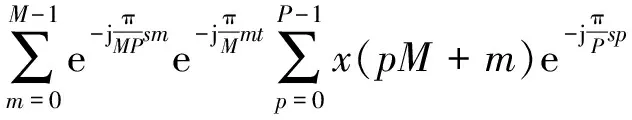
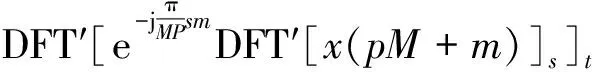
(11)
其中内层DFT′[.]在t为奇、偶2种情况下,可通过2倍抽取简化为同一个子模块进行计算,改进后的多相结构如图3所示。
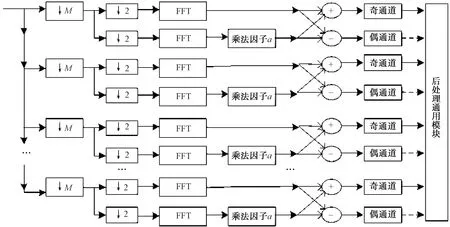
图3 改进的多相FFT
采用多相结构使得数据率降低,数据进入奇、偶通道后,奇通道、偶通道可分时复用后处理通用模块。相比传统多相架构,本文提出的结构实现了功能分治:多相结构划分奇偶子模块实现,且各子模块相互独立,奇、偶信道分别独立输出,而传统多相FFT中奇偶信道互相耦合,需要同时经过FFT后处理。图4给出了图3中提到的后处理(奇通道、偶通道均采用该模块)通用模块。
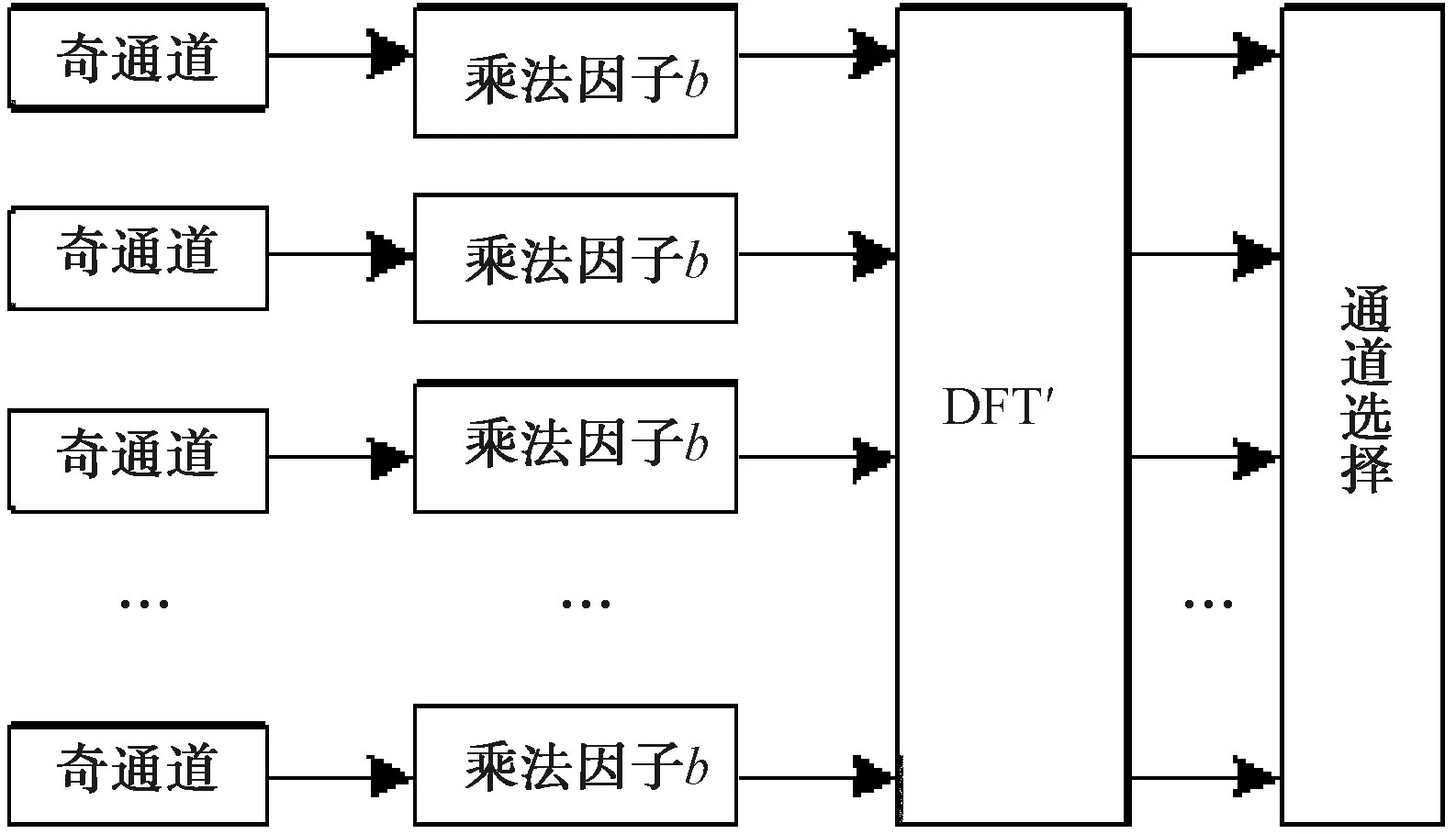
图4 后处理通用模块
3 仿真试验
仿真实验主要分为2个部分,首先仿真验证传统多相FFT的有效性;其次仿真验证本文多相FFT结构的有效性。
仿真1:传统FFT
采样率为1 000 MHz,信号频率218 MHz,256个采样点,信道总数取16。
将多相FFT各信道拼接,图5给出了拼接的频谱与直接FFT频谱的对应关系,可以看出多相FFT与直接FFT在结果上完全一致。
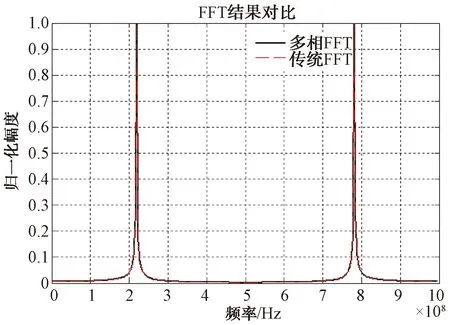
图5 多相FFT与传统FFT对比
多相FFT仿真结果如图6所示,可以看出信号分别落在第4、13两个信道,且信道1~8与信道9~16在幅值上互为镜像。从图5、图6的结果可以看出多相FFT既有传统FFT的功能,又可以划分子信道。
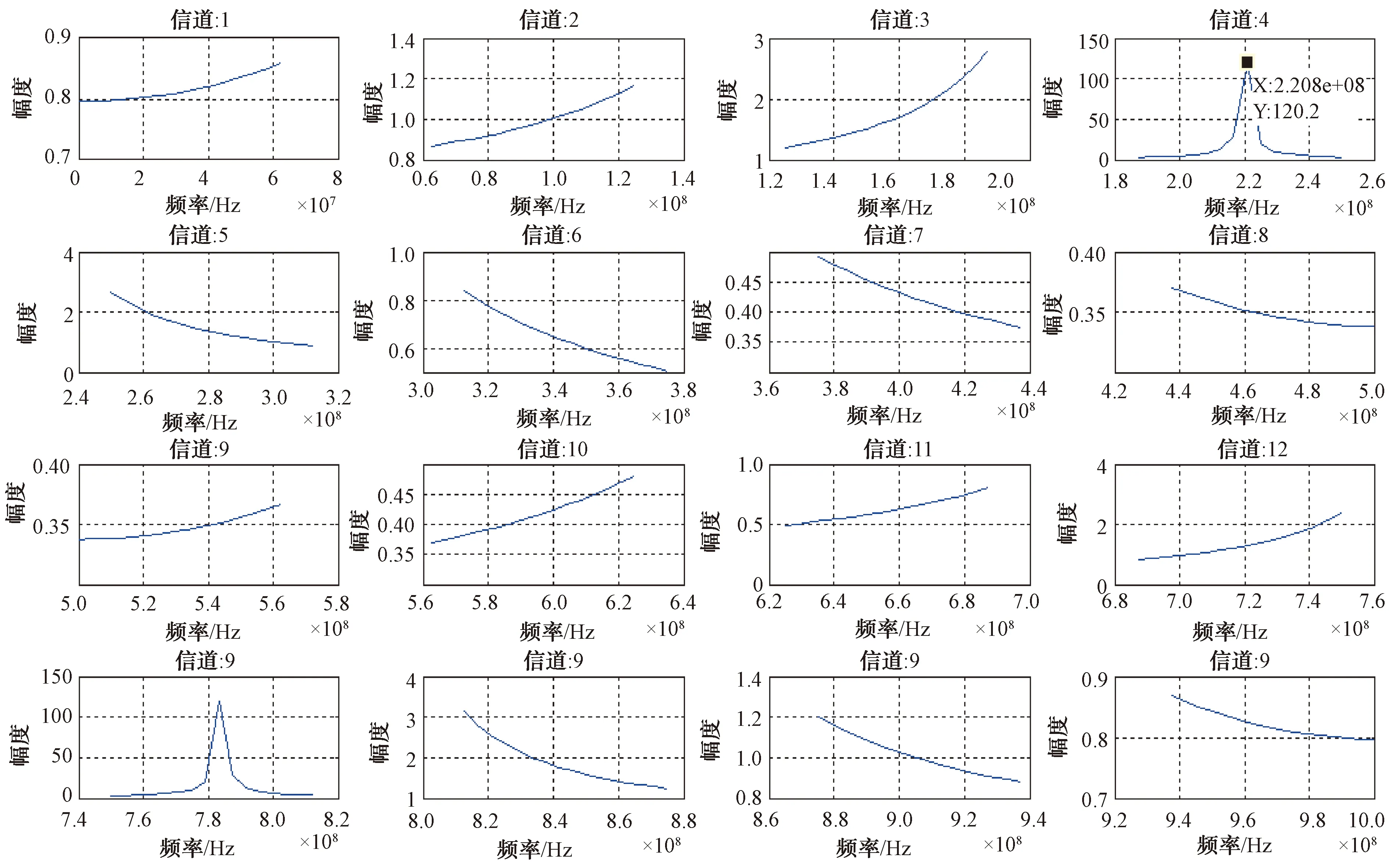
图6 多相FFT各信道输出
仿真2:改进多相FFT实现
采样率为1 000 MHz,信号频率373 MHz,256个采样点,信道总数取16。
图7给出了改进多相FFT实现结果,从图7可以看出该结构与传统FFT完全等价。图6给出了奇偶信道经过后处理的输出结果,其中奇偶信道的结果分别计算得出,二者相互独立,并且奇信道、偶信道共用同一个后处理模块。根据结果可以观察到改进的多相FFT频谱由奇偶信道的频谱拼接而成,对于输入信号为实数信号的场景,该结构仅计算[0,fs/2]的频域信息,并仅考虑奈奎斯特域对应的频域信息。
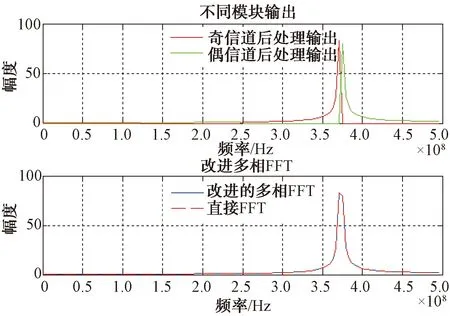
图7 改进多相FFT结果图
4 结束语
本文在传统FFT基础上,首先分析多相FFT实现思路,并进一步提出了改进的多相FFT结构。
该结构主要有2个创新点:(1)借助基本多相结构,仅分析奈奎斯特域对应的频域信息;(2)信号的奇偶信道可实现分治。实验结果证明了本文思路的合理性以及算法的有效性。
[1] HARRIS F J,DICK C.Digital receivers and transmitters using polyphase filter banks for wireless communications[J].IEEE Transactions on Microwave Theory and Techniques,2003,51(4):115-121.
[2] 宗孔德.多抽样率信号处理[M].北京:清华大学出版社,1996.

