合理设计环节 清晰体验过程
赵丹 景敏
[摘 要]
关注知识形成中的“猜想”、“验证”、“应用”过程是现行课程的一大亮点。通过对一节课的视频分析,说明教师对这一过程关注不够,过程不清晰,甚至混乱的状况。
[关键词]
初中数学;验证;应用
《义务教育数学课程标准(2011年版)》指出:“学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。”就数学原理性知识来说,教学过程应该让学生经历“猜想—验证(证明)—应用”的过程。但是,在日常数学课堂教学中,教师还没有充分认识到数学活动过程的重要性,甚至有时候还会混淆活动环节的差异,比如猜想、验证、应用之间的关系,这势必会影响学生对数学过程的理解。
一、课例简要说明
本文以锐角三角函数正切为例,分析教师对新知识形成过程的认识。文中的教学片段来源于“第十届初中青年数学教师优秀课展示与培训活动”的一节课,其内容选自“北师大版”义务教育教科书九年级下册《直角三角形的边角关系》的第一节《锐角三角函数》(第1课时)。
从教学设计看,新知识生成过程经历如下几个阶段:教师首先复习了与直角三角形有关知识。然后,教师从现实生活问题情境——梯子摆放陡缓问题引入本课。接下来,通过实验探究,教师引导学生寻找刻画梯子陡缓程度的量:倾斜角和铅直高度与水平宽度的比值。此后,通过例题进一步揭示倾斜角与铅直高度与水平宽度的比值的关系,并引出正切概念。
从上述过程看,虽然教师关注了学生经历数学知识形成的过程。但对例题处理方式上值得商榷。
二、教学片段描述及过程分析
(一)“探究活动一”的教学片段及分析
1.教学片段描述
首先,教师以靠在墙边的梯子作为实际问题情境,通过探讨摆放梯子陡缓程度引入本节课。其次,教师组织学生进行实验探究活动:用课本比作墙壁,尺子比作梯子,模拟梯子由“缓”变“陡”的过程。同时思考问题:梯子在上升变“陡”的过程中,什么量决定梯子的倾斜程度。在学生动手实验和独立思考的基础上,组内再进行交流。最后,通过抢答方式,两名学生汇报如下学习成果:
生1说道:倾斜角的大小决定梯子的倾斜程度;铅直高度与水平宽度的比值决定梯子的倾斜程度。
生2进一步明确道:倾斜角越大,梯子越陡;铅直高度与水平宽度的比值越大,梯子越陡。
听了学生的回答后,教师对学生的精彩发言给予赞赏。同时,同学们也自发地给予发言同学以掌声。随后,教师复述学生2的发现,并将学生的发现呈现在大屏幕上。
本环节共用时3分钟,其中实验研讨1分40秒左右,小组汇报1分20秒左右。
2.教学片段分析
(1)教师需关注学生发现的思维过程。学生的探索发现过程用时仅1分40秒左右。对学生极富成效的发现,教师十分赞赏。但遗憾的是,教师没有进一步追问学生是怎样发现或想到这两个量的,特别是,怎样想到梯子倾斜程度与铅直高度与水平宽度的比值有关系。众所周知,探索发现是思维创新的过程,因此,了解学生探索中的思维活动,并让他们表述出来,这对学生创新思维能力的发展是极为有益的。
(2)教师需及时明确,发现只是一种猜想。通过动手实验所获得的成果只是一种数学猜想,这一点必须清楚说明,以突显验证或证明的意义。但在这个环节,教师没有明确指出学生的发现仅仅是一种猜想。
(3)教师对猜想的条件和结论强调不够。如果要更好地开展验证环节,这里需要教师进一步分析和强调猜想成立的条件和结论。因为,验证活动是通过具体实例,在其满足猜想的条件的前提下,判断猜想的结论是否成立的过程。
此外,教师没有板书学生获得的结论,而是呈现在大屏幕上。由于屏幕上的內容不会长时间保留在学生的视线范围内,所以,这种记录方式会对后一阶段的活动带来不便。
(二)例题的教学片段及分析
对学生的发现进行小结后,教师提出:我们再用几个例子一块来感受一下倾斜角以及铅直高度与水平宽度的比对梯子倾斜程度的影响。接着,教师先后呈现了四个例题。
1.教学片段描述
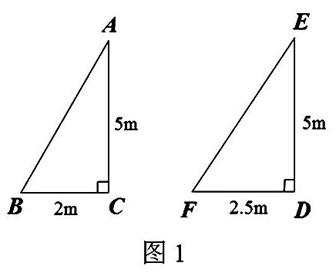
例1:(如图1)梯子AB和EF哪个更陡?你是怎样判断的?
生3:通过这两幅图可以看到,这两幅图的铅直高度是相同的,可以通过比较水平宽度来判断梯子是陡还是缓。因为△ABC的水平宽度是2(米),△EFD的水平宽度是2.5(米),△ABC的水平宽度更短一些,所以我认为梯子AB更陡。
师:他只是解释一下铅直高度一样前提下,看水平宽度。如果根据刚才的结论(猜想),你再看一看,5/2和5/2.5谁大?
生3:5/2大一些(此时学生略显不解教师的追问)。
师:那显然这个梯子(AB)就要比这个梯子(EF)更陡一些,也就是AB比EF更陡。
生4:还可用以前(学习过的)平移的思想,让两个三角形的铅直高度重合,通过比较倾斜角的大小,就可以知道哪一个梯子更陡。
教师利用信息技术手段移动△ABC,使得AC与ED重合,使学生直观地看到∠ABC与∠EFD谁大谁小,并进一步总结道:通过比较倾斜角的大小,可以知道哪一个梯子更陡。
例2:(如图2)梯子AB和EF哪个更陡?你是怎样判断的?
生5:我认为第二个梯子,就是FE更陡一些。因为两个三角形的水平宽度是一样的,都是2米,这就需要把他们的铅直高度相比, ED更高一些,所以我认为EF更陡。
师:水平宽度是一样的,直接比的是(AC和ED)。那铅直高度与水平宽度的比值呢?
生5:EF:FD的比值要比AC:BC的比值要大。
师:就是说,5:2要小于6:2,所以EF陡。
师:也可以用前面说的平移的方法。
生:可以。
师:总而言之,通过这个(例子)可以发现,铅直高度与水平宽度的比值越大,梯子越陡;角度越大,梯子也越陡。
由于教师反复引导,在此后呈现的例3和例4中,学生开始直接应用猜想解决问题。
2.教学片段分析
首先,从本节课教学设计看,通过“探究活动一”获得探索发现后,设计四个例子的意图是,应用探索发现的结果,以便为探索倾斜角与其对边和邻边(铅直高度与水平宽度)比值的关系做铺垫这样的设计。从新课程倡导的“猜想—验证或证明—应用”的思维范式来看,在学生获得猜想以后,下一步应该是验证猜想或证明猜想,然后才能进入到应用阶段。如果从猜想直接进入到应用阶段,那么可能会给学生体验“猜想—验证或证明—应用”的过程带来消极影响。
其次,按照教师的设计意图来看,学生最初并没有理解例题的设计意图。我们看到,学生3最初判断梯子倾斜程度的依据是,当铅直高度一致时,水平宽度大小决定梯子陡缓程度。对于教师追问 “5/2和5/2.5谁大”时,学生3对教师的问题略微显示出不解其意图的神态。另外,学生5的表现与学生3的表现如出一辙。由此可见,学生3和学生5都把问题作为一种特殊情况加以探究了。
之所以出现这种现象,究其原因,一是教师对探索发现的结果强调的不到位,因此没有引起学生对条件和结论的关注。二是从猜想过渡到例题时,教师没有明确说明做例题的意图。教师说:“我们再用几个例子一块来感受一下倾斜角以及铅直高度与水平宽度的比对梯子倾斜程度的影响。”此处教师用“感受”一词,其含义不清晰。
三、改进建议
首先,获得猜想后要对猜想进行分析,找出条件和结论,并以板书形式记录下来,以此引起学生对猜想的注意。
其次,進入验证阶段,教师要给出清晰而明确的信号:接下来,我们要对猜想进行验证。借助于这样的过渡语引起学生的注意。
再次,验证过程需要分三步进行:第一步,分别计算两个梯子的倾斜角大小或铅直高度与水平宽度的比值大小。第二步,通过观察,直观判断哪一个梯子倾斜程度大。第三步,判断倾斜角大的梯子是否倾斜程度大;铅直高度与水平宽度的比值大的梯子是否倾斜程度大。通过这样的过程可以让学生深入理解验证的含义,掌握验证的思维特点。
[参 考 文 献]
[1]熊惠民.中学数学教学设计与案例研究[M].北京:科学出版社,2014.
[2]中华人民共和国教育部.全日制义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
[3]义务教育数学课程标准数学教科书[M].北京:北京师范大学出版社,2016.
(责任编辑:张华伟)

