基于改进混合蛙跳算法的梯级水库优化调度

，， ， ， ,(.华北电力大学 可再生能源学院， 北京 02206； 2.长江勘测规划设计研究有限公司，武汉 000；.中国电建集团 北京勘测设计研究院有限公司， 北京 0002；.中国水利水电科学研究院， 北京 0008)

1 研究背景

目前，我国各大江河干流及其主要支流等已经或正在形成各自的水库群，为水资源高效利用发挥着越来越重要的作用[1]，并有力地服务于全面建设小康社会。梯级水库间具有十分复杂的水力联系和电力联系，其联合优化调度是一个多约束、高维、非线性的系统优化问题，一直备受关注[2]。目前，大量寻优算法已被用于水库调度领域，其中动态规划法具有全局收敛性，是求解梯级水库联合优化调度模型的经典算法，但其面临“维数灾”问题[3]；近年来，随着人工智能学科的发展，粒子群算法[4]、遗传算法[5]、人工鱼群算法[6]等智能方法已被广泛引入，表现出强劲的生命力，但也存在早熟收敛等不足。因此，研究新方法并尝试解决梯级水库优化调度问题仍然具有极为重要的现实意义。

受青蛙群体的协同机制启发，Eusuff和Lansey[7]提出了一种新型高效的启发式智能算法——混合蛙跳算法(Shuffled Frog Leaping Algorithm，SFLA)。该算法能够搜索分析复杂空间中的最优值，具有参数少、性能高、鲁棒性强等特点，可用于求解具有不可微、多约束、多变量、多目标等特点的非线性最优控制问题。但是，SFLA存在着易早熟收敛等缺陷，已有学者对其进行了一些改进，提出了扩张蛙跳算法[8]、粒子群蛙跳算法[9]、云变异蛙跳算法[10]等改进算法，取得了良好效果。

对SFLA及其改进的算法作进一步分析，发现研究多是针对算法中的局部信息交流或者全局信息交换2种策略中的一种进行改进，算法的寻优性能仍有待进一步提高。基于此，本文利用混沌技术对子群最优解进行精细搜索，结合蛙群最优值扰动的处理方式对算法收敛进行有目的的指导，构建了“局部精细搜索”与“全局激励调节”协同作用的改进机制，并将其融入SFLA中，提出了一种改进混合蛙跳算法(An Improved Shuffled Frog Leaping Algorithm，AISFLA)，以统筹算法的局部勘探和全局搜索。以李仙江流域梯级水库为研究实例，验证了AISFLA的可行性和有效性。

2 混合蛙跳算法机理

SFLA是一种基于群体的协同搜索方法[11]，模拟青蛙觅食过程进行寻优。首先，按既定规则将青蛙种群分成多个子群，并在子群中开展搜索，通过信息的内部交流来优化内部个体；然后，融合所有子群并按优劣顺序对青蛙个体进行排序，再次按既定规则划分青蛙种群，通过这种方式实现全局性的信息交换。可以看出，混合蛙跳算法主要依靠局部信息交流和全局信息交换的结合搜索机制来寻优，可在一定程度上避免过早陷入局部极值点。几个重要概念见表1。

表1 SFLA重要概念Table 1 Important concepts in Shuffled Frog LeapingAlgorithm(SFLA)

SFLA计算流程如图1所示，关键步骤包含蛙群初始化、蛙群划分、局部搜索以及全局信息交换等。设f(x)为适应度函数;Ω为可行域;每一次迭代中，Xg为蛙群最优青蛙;Xb为各子群最好青蛙;Xw为各子群最差青蛙。算法采用如下更新策略在各子群中进行局部搜索：

(1)

式中：Dj为蛙跳步长更新值；rand()为[0,1]之间的随机数；Xw,new为更新后的子群最差青蛙。

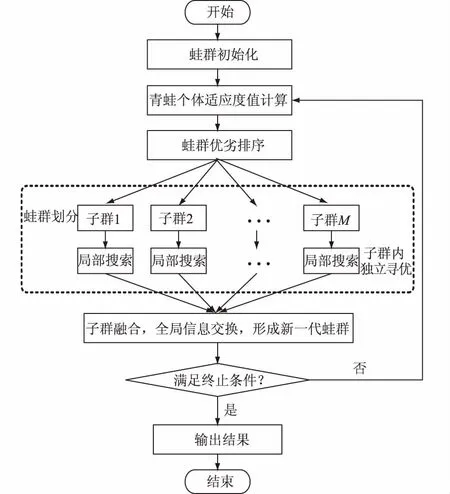
图1 SFLA计算流程Fig.1 Computation flow of SFLA

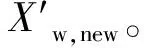
3 改进混合蛙跳算法

SFLA提出的时间不长，在理论方法及其应用研究方面尚有待探索完善。与多数智能算法类似，SFLA在寻优过程中不断向蛙群最优位置靠拢，蛙群多样性逐渐降低，易出现早熟收敛。针对SFLA存在的问题，对局部搜索和早熟收敛进行改进，提出一种改进混合蛙跳算法(AISFLA)。

3.1 局部精细搜索策略

混沌运动普遍存在于非线性系统中，具有随机性、遍历性和规律性等特点。鉴于此，混沌技术具有易实现和避免局部陷阱的特殊能力[12]，已与多种智能算法融合来提高其性能。本文选用一种简洁高效的一维非线性映射模型，即

Cr(t+1)=aCr(t)(1-Cr(t)) 。

(2)

式中：Cr(t)是算法每次运行时随机产生的常数;a为控制参数，一般取4，此时系统处于混沌状态[6]。

运用混沌技术，在每次子群最好青蛙Xb周围进行精细搜索，策略如下：

newxb=xb+αs;

(3)

(4)

s=Cr(U-L)/β。

(5)

式中：α是搜索方向因子；s是搜索尺度；β是缩放因子，为不错过各子群最好青蛙附近可能存在的更优个体，其值可取20[13]；U，L分别为搜索空间的上下限。

3.2 全局激励调节

针对算法寻优过程中易出现早熟的问题，提出一种全局激励调节策略，以改善蛙群多样性，提高全局信息交流的能力。

3.2.1 蛙群相对多样性判断

(6)

(7)

式中：f为归一化因子；F为蛙群规模。

设μk为当前蛙群相对多样性表征参数，可表示为

μk=σk/σ0。

(8)

若μk小于预定阈值μ*，则说明此时蛙群的多样性较差，蛙群因受限在某一超平面中而过早收敛[15]，此时需要对蛙群最优青蛙个体Xg进行扰动来改善蛙群多样性，进而提高全局寻优能力。

3.2.2 蛙群最优个体处理

文献[16]在处理PSO算法的早熟收敛问题时，采用了对当前全局最优粒子进行微扰的方式进行处理，效果显著。借助这种思想，本文对蛙群最优个体进行扰动，促使算法跳出局部最优。扰动公式为

(9)

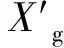
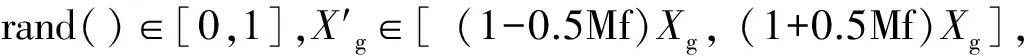
4 AISFLA在梯级水库优化调度中的应用

4.1 梯级水库优化调度模型

4.1.1 目标函数

以发电量最大为目标，建立梯级水库中长期优化调度模型，其目标函数为

(10)

式中：E为调度期内总发电量；i，n分别为水电站的编号和总数；t，T分别为调度期内的时段编号和总时段数；Ai为水电站i的出力系数；Qi,t为水电站i在时段t的发电流量；Hi,t为水电站i在时段t的平均发电水头；Δt为时段长。

4.1.2 约束条件

(1)水量平衡约束

Vi,t+1=Vi,t+(Ii,t-Qi,t-Si,t)Δt。

(11)

式中：Vi,t，Vi,t+1分别为水电站i在时段t的初、末库容；Ii,t，Si,t分别为水电站i在时段t的入库流量、弃水流量。

(2)上下库流量联系

Ii,t=Qi-1,t+Si-1,t+Ri,t。

(12)

式中Ri,t为水电站i在时段t的区间入库流量。

(3)水位约束

Zi,tmin≤Zi,t≤Zi,tmax。

(13)

式中：Zi,t为水电站i在时段t的水位；Zi,t min，Zi,t max分别为水电站i在时段t允许的最低、最高水位。

(4)出力约束

Ni,tmin≤Ni,t≤Ni,tmax。

(14)

式中：Ni,t为水电站i在时段t的出力；Ni,t min，Ni,t max分别为水电站i在时段t的出力下限、上限。

(5)下泄流量约束

qi,tmin≤Qi,t+Si,t≤qi,tmax。

(15)

式中qi,t min，qi,t max分别为水电站i在时段t的下泄流量下限、上限。

(6)始末水位约束

(16)

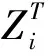
4.2 基于AISFLA的模型求解步骤

运用AISFLA求解梯级水库中长期优化调度模型，每只青蛙表示一种调度策略，具体求解步骤如下所述。

步骤1：参数初始化设置，包括蛙群规模F，子群中青蛙数h(F=M×h)，子群迭代次数Num_local，蛙群迭代次数Num_general。可行域Ω范围内随机产生F只青蛙，第j只青蛙Xj编码为

(17)

式中xit(i=1,2,…,n；t=1,2,…,T) 表示水电站i在时段t的出力。

步骤2：以式(10)为适应度函数，计算当前所有青蛙个体的适应度值，然后按优劣顺序进行排序，并对蛙群进行重新划分。

步骤3：利用式(3)—式(5)在当前子群最好个体Xb基础上进行精细搜索，更新并取代Xb；确定当前蛙群最优个体Xg，然后依据式(1)的搜索策略更新子群最差个体Xw，重复步骤3直至满足子群迭代次数Num_local；计算当前蛙群适应度方差。

步骤4：计算蛙群相对多样性参数μk，检验当前蛙群多样性是否满足预定阈值。如果μk<μ*，利用式(9)进行扰动，转入步骤2；否则，转入步骤5。

步骤5：判断算法是否达到最大迭代次数Num_general。如果满足，则停止寻优过程，输出结果；否则，转入步骤2继续迭代。

算法流程见图2。

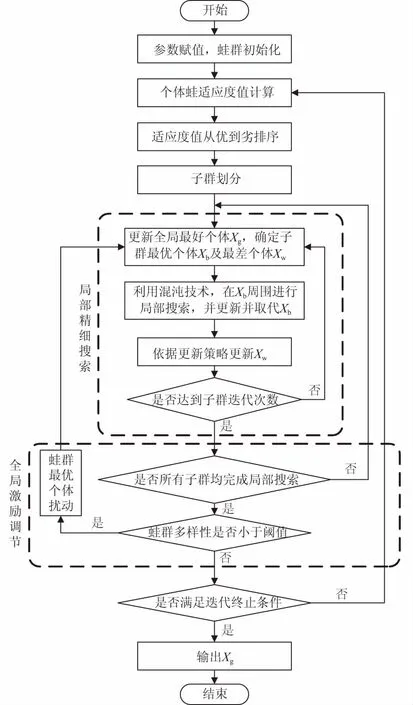
图2 AISFLA计算流程Fig.2 Computation flow of AISFLA

表2 李仙江梯级水库基本参数Table 2 Basic parameters of Lixianjiang cascade reservoirs

5 实例研究

5.1 工程概况

李仙江位于云南省境内，是红河的一级支流，控制流域面积约19 309 km2，中国境内干流全长473 km，天然落差约1 790 m。干流上依次修建崖羊山、石门坎、新平寨、龙马、居甫渡、戈兰滩、土卡河7座水库，本文选取具有调节性能的3座水库(崖羊山、石门坎、龙马)进行计算，基本参数见表2。

5.2 结果分析

以某一枯水年实测径流过程为输入项，分别采用理论较为成熟的PSO算法、逐次逼近动态规划算法(DPSA)、标准SFLA算法以及本文所提AISFLA算法，在同等条件下对李仙江梯级水库进行仿真计算。参照文献[10]和文献[15]中的参数设置建议，设置如下的算法参数：AISFLA中，蛙群规模F=200，子群中青蛙数h=20，子群总数M=10，子群迭代次数Num_local=10，蛙群迭代次数Num_general=500，蛙群相对多样性阈值μ*=0.4，激励因子Mf=1.5；标准SFLA中，参照AISFLA进行参数设置；PSO中，学习因子c1，c2分别取1.5，2.0，惯性权重w=0.5，迭代次数取500；DPSA水位离散点取100。各智能算法独立运行10次，统计10次运算中各种方法的最大发电量、平均发电量和标准差等指标，结果如表3所示。可以看出，与表中列举的2种智能优化算法相比，AISFLA的计算结果有明显提高(且最接近DPSA优化结果)，与此同时，寻优结果的稳定性得到了有效提升，如相比于SFLA和PSO，AISFLA的标准差分别降低了70.17%和72.22%。

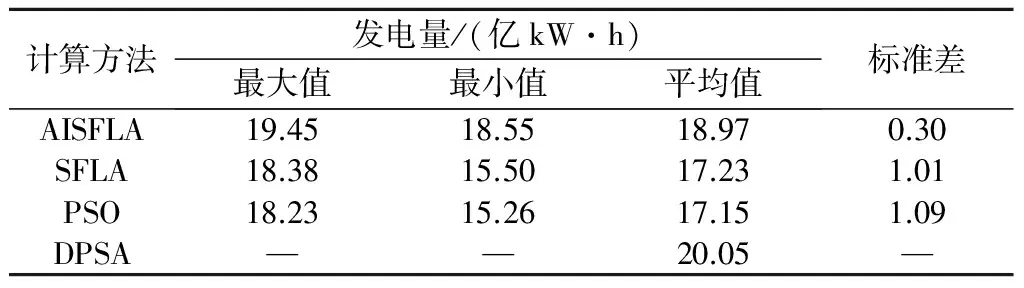
表3 不同方法计算结果Table 3 Results computed by different methods

进一步对AISFLA和SFLA寻优结果进行分析。图3为2种算法独立运行10次的计算结果(按降序排列)，可以看出，AISFLA相比于SFLA具有更好的寻优性能，其各次模拟结果均优于SFLA，且均值(平均发电量)比SFLA增加了1.74亿kW·h，增幅为10.08%。

图3 AISFLA算法与SFLA算法10次模拟结果对比Fig.3 Comparison of result between AISFLA and SFLA after 10 times of simulation

从收敛性方面分析AISFLA的优越性。图4为3种智能算法最大发电量方案对应的收敛过程，可以看出，SFLA结果较优于PSO，其收敛速度却相对较慢，SFLA和PSO两种算法在寻优过程中容易陷入到局部最优中，二者收敛过程呈现明显的阶梯状；AISFLA在SFLA基础上，利用混沌技术对局部最优解进行变异，加之结合全局激励调节作用对收敛进行有目的指导，“局部”与“全局”耦合作用的改进机制，保证了算法求得的最终结果更接近全局最优解；同时，AISFLA较SFLA和PSO算法的收敛速度更快。

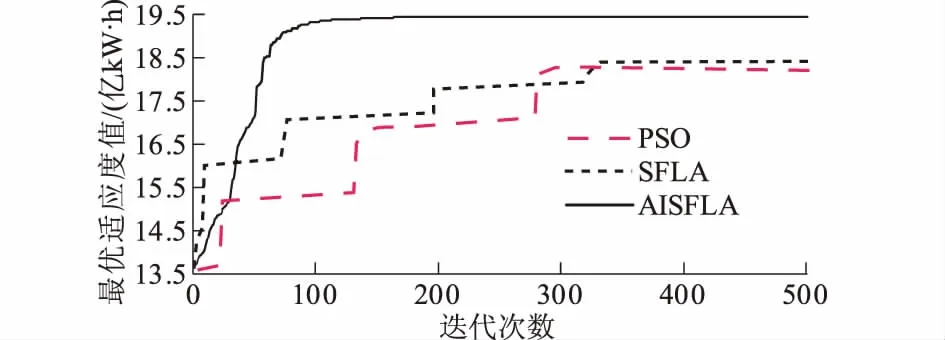
图4 3种算法收敛性比较Fig.4 Comparison of convergence among different methods

5.3 AISFLA性能进一步测试

选取李仙江流域1957—2000年径流资料进行长系列计算，进一步测试AISFLA在求解梯级水库中长期优化调度模型时的性能，计算结果如表4所示。可以看出，与SFLA和PSO相比，AISFLA求得多年平均发电量的增幅分别为6.74%和7.51%，所得结果更好，算法继续保持着较好的寻优性能。

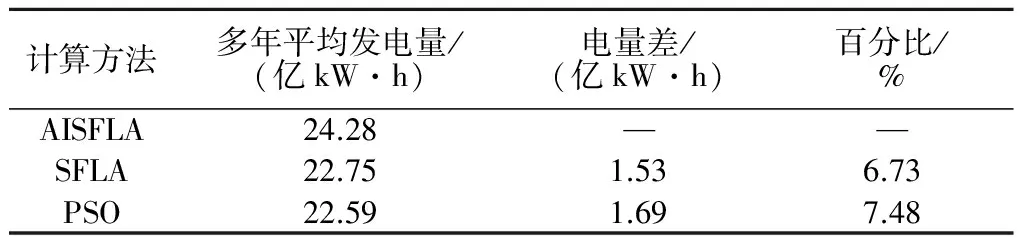
表4 长系列计算结果Table 4 Computation results of AISFLA forlong-term series

注：电量差=AISFLA-SFLA(或者PSO)；百分比=电量差/SFLA(或者PSO)×100%

综上，在水库调度仿真计算中，本文所提AISFLA明显改善了SFLA寻优目标和收敛速度2方面特性，是一种有效的改进算法。

6 结 语

混合蛙跳算法(SFLA)是一种基于群体的协同搜索方法，本文提出了利用“局部精细搜索”和“全局激励调节”耦合改进策略对SFLA进行改进。一方面利用混沌技术对子群最优值进行变异操作，另一方面通过对蛙群最优值进行扰动来维持种群多样性。对李仙江流域的计算结果表明，改进算法具有很好的寻优能力，可有效地增加已建成水库群的发电效益，为提高梯级水库中长期调度水平提供了技术支持。扩展算法应用领域是下一步研究的重点。

参考文献：

[1] 王本德, 周惠成, 卢 迪. 我国水库(群)调度理论方法研究应用现状与展望[J]. 水利学报, 2016, 47(3): 337-345.

[2] JI Chang-ming, JIANG Zhi-qiang, SUN Ping,etal. Research and Application of Multidimensional Dynamic Programming in Cascade Reservoirs Based on Multilayer Nested Structure[J]. Journal of Water Resource Planning and Management, 2015, 141(7): 1-13.

[3] 王 成, 曹庆磊. 水库运行管理中优化调度的计算机算法研究[J]. 长江科学院院报, 2011, 28(1): 66-70.

[4] 王 森,马志鹏,李善综,等.粗粒度并行自适应混合粒子群算法及其在梯级水库群优化调度中的应用[J]. 长江科学院院报, 2017, 34(7): 149-154.

[5] 陈 端, 陈求稳, 陈 进. 基于改进遗传算法的生态友好型水库调度[J]. 长江科学院院报, 2012, 29(3): 1-6,12.

[6] 黄 锋, 王丽萍, 向腾飞, 等.基于混沌人工鱼群算法的水库发电优化调度研究[J]. 中国农村水利水电, 2014, (10): 149-153.

[7] EUSUFF M, LANSEY K, PASHA F. Shuffled Frog-leaping Algorithm: A Memetic Meta-heuristic for Discrete Optimization[J]. Engineering Optimization, 2006, 38(2): 129-154.

[8] KAUR P, MEHTA S. Resource Provisioning and Work Flow Scheduling in Clouds Using Augmented Shuffled Frog Leaping Algorithm[J]. Journal of Parallel and Distributed Computing, 2017, 101: 41-50.

[9] SAMUEL G G, ASIR RAJAN C C. Hybrid: Particle Swarm Optimization-Genetic Algorithm and Particle Swarm Optimization-Shuffled Frog Leaping Algorithm for Long-term Generator Maintenance Scheduling[J]. International Journal of Electrical Power & Energy Systems, 2015, 65: 432-442.

[10] 王丽萍, 孙 平, 蒋志强, 等. 基于并行云变异蛙跳算法的梯级水库优化调度研究[J]. 系统工程理论与实践, 2015, 35(3): 790-798.

[11] 罗雪晖, 杨 烨, 李 霞. 改进混合蛙跳算法求解旅行商问题[J]. 通信学报, 2009, 30(7): 130-135.

[12] 阳春华, 钱晓山, 桂卫华. 一种混沌差分进化和粒子群优化混合算法[J]. 计算机应用研究, 2011, 28(2): 439-441.

[13] 易文周, 田立伟. 一种基于混沌搜索和鲶鱼效应策略的粒子群算法[J]. 计算机应用与软件, 2013, 30(5): 311-315.

[14] 姜 伟, 王宏力, 何 星, 等. 并行免疫离散粒子群优化算法求解背包问题[J]. 系统仿真学报, 2014, 26(1): 56-61.

[15] 纪昌明, 刘 方, 彭 杨, 等. 基于鲶鱼效应粒子群算法的水库水沙调度模型研究[J]. 水力发电学报, 2013, 32(1):70-76.

[16] 金荣洪, 袁智皓, 耿军平, 等. 基于改进粒子群算法的天线方向图综合技术[J]. 电波科学学报,2006, 21(6): 873-878.