基于最大熵投影寻踪模型的云南省近10 a水资源承载力评价
,(云南省水利水电勘测设计研究院,昆明 650021)
1 研究背景
水资源承载力是指一个国家或区域在某一历史发展阶段内,水资源可以维持的最大经济规模和人口数量,是衡量区域水资源支撑经济社会可持续发展能力大小的重要指标之一[1]。目前用于水资源承载力评价的综合方法有模糊分析法[2]、主成分分析法[3]、层次分析法[4]、物元分析法[5]、集对分析法[6]和神经网络评价法[7]等。由于水资源承载力评价涉及水资源、社会经济、生态环境等领域,属多指标、非线性复杂系统问题,这些方法和模型各有优势和特点,但也存在不足,如:模糊分析法由于模糊隶属度值之间较为接近,不易区分各个评价区域;主成分分析法易造成评价指标信息的丢失;层次分析法存在人为确定指标权重的不足;物元分析法需要构造较多的评价函数,且函数设计无规律可循;集对分析法需人为确定各评价指标的分类等级,存在一定的主观性,同时存在同、异、反标准的确定和相异度系数合理取值的困难;BP神经网络评价法存在训练样本难以获取、权阈值参数较难确定以及算法易陷入局部极值等不足。投影寻踪(Projection Pursuit,PP)技术是将高维数据投影到低维空间,并在低维空间进行数据分析研究的统计方法,已在水资源承载力评价中得到应用[8-9]。然而,PP技术在实际应用中需解决好2方面的问题:一是传统粒子群优化(Particle Swarm Optimization,PSO)等算法在用于PP最佳投影方向优化中存在早熟收敛、易陷入局部极值等问题;二是传统PP技术是以投影值标准差与类内密度之积最大为优化目标,忽略了投影向量分布的不确定性、随机性和评价指标间的相关性,可能导致评价或分类能力下降的问题[10]。
为能有效解决PP技术在水资源承载力评价中的不足,从水资源系统、经济社会系统、生态系统3个方面构建水资源承载力评价指标体系和分级标准,提出基于信息熵理论改进的最大熵投影寻踪(Maximum Entropy Projection Pursuit,MEPP)技术,利用混合蛙跳算法(Shuffled Frog Leaping Algorithm,SFLA)优化MEPP最佳投影方向,提出SFLA-MEPP水资源承载力评价模型,并构建生物地理优化(Biogeography-Based Optimization,BBO)算法-MEPP、和声搜索(Harmony Search,HS)算法-MEPP和PSO-MEPP评价模型作对比,以云南省近10 a水资源承载力评价为例进行实例分析,旨在验证SFLA-MEPP模型应用于水资源承载力评价中的可行性和有效性。
2 水资源承载力评价指标体系及分级标准
近年来,国内外开展水资源承载力评价分析的相关研究较多[1-9,11-13],但由于评价区域之间水资源禀赋、经济社会发展水平、用水效率等存在较大差异,加之水资源承载力评价涉及水资源、经济社会、生态环境等多方因素,属多指标、高维、非线性系统问题,目前尚未形成普遍认同的指标体系和分级标准。笔者充分考虑区域水资源特点及经济社会发展状况,遵循科学性、可操作、可量化以及指标可获取等原则,从水资源系统、经济社会系统和生态系统筛选14个指标构建具有目标层A、准则层B和指标层C的区域水资源承载力评价指标体系和“绝对可承载(Ⅰ级)”、“可承载(Ⅱ级)”、“基本可承载(Ⅲ级)”、“不可承载(Ⅳ级)”4个等级的分级标准,见表1。
表1水资源承载力评价指标体系及分级标准
Table1Ratingcriterionforindicatorsofwaterresourcescarryingcapacity
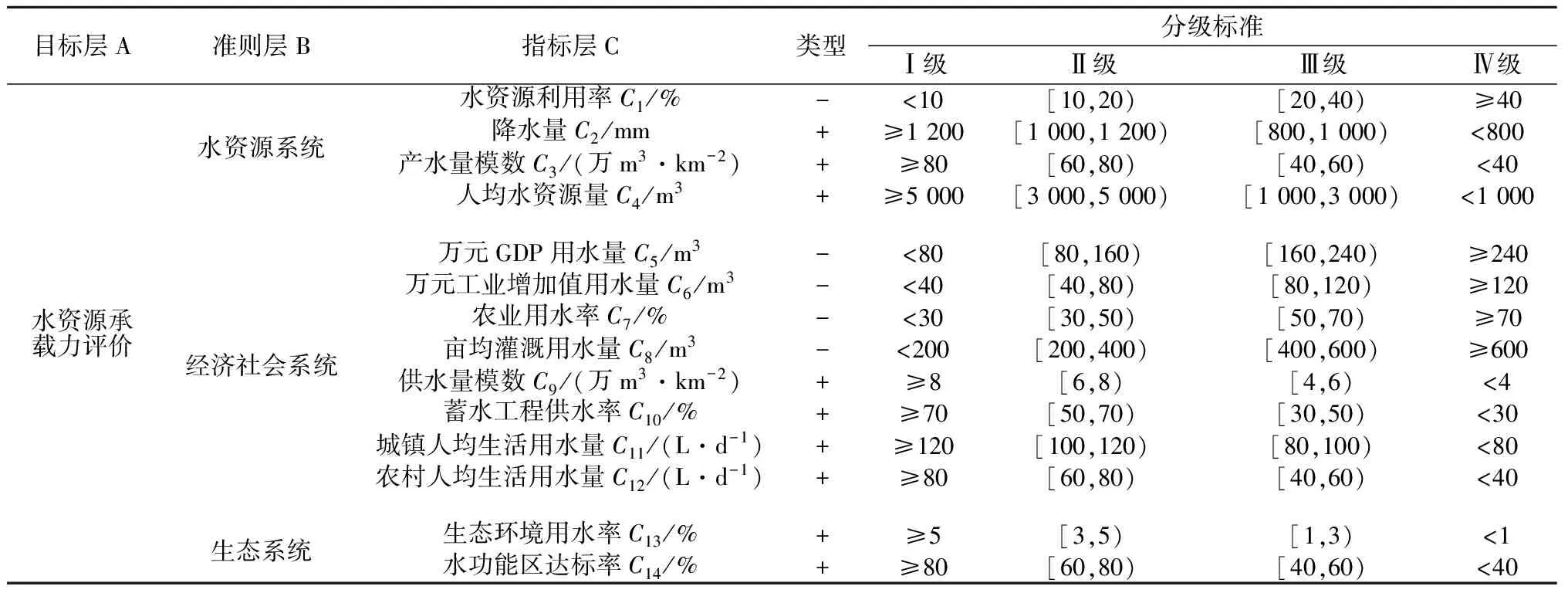
目标层A准则层B指标层C类型分级标准Ⅰ级Ⅱ级Ⅲ级Ⅳ级水资源承载力评价水资源系统经济社会系统生态系统水资源利用率C1/%-<10[10,20)[20,40)≥40降水量C2/mm+≥1200[1000,1200)[800,1000)<800产水量模数C3/(万m3·km-2)+≥80[60,80)[40,60)<40人均水资源量C4/m3+≥5000[3000,5000)[1000,3000)<1000万元GDP用水量C5/m3-<80[80,160)[160,240)≥240万元工业增加值用水量C6/m3-<40[40,80)[80,120)≥120农业用水率C7/%-<30[30,50)[50,70)≥70亩均灌溉用水量C8/m3-<200[200,400)[400,600)≥600供水量模数C9/(万m3·km-2)+≥8[6,8)[4,6)<4蓄水工程供水率C10/%+≥70[50,70)[30,50)<30城镇人均生活用水量C11/(L·d-1)+≥120[100,120)[80,100)<80农村人均生活用水量C12/(L·d-1)+≥80[60,80)[40,60)<40生态环境用水率C13/%+≥5[3,5)[1,3)<1水功能区达标率C14/%+≥80[60,80)[40,60)<40
注:“+”表示正向指标,指标值越大,其水资源承载力越大;“-”表示负向指标,指标值越小,其水资源承载力越大
3 SFLA-MEPP水资源承载力评价模型
3.1 MEPP技术
PP技术在各行业领域应用广泛,但传统PP技术由于忽略了投影向量分布的不确定性和评价指标在一定程度上存在的相关性,从而可导致评价或分类能力下降[10]。信息熵理论认为,在仅有部分信息的条件下要对概率分布做出推断,最有效的方法是使信息熵值最大,即熵值越大,人为造成的约束和假设越少[14]。本文利用最大熵改进传统PP技术,提出最大熵投影寻踪(MEPP)技术。MEPP技术用于水资源承载力评价简述如下[10,14-15]。
3.1.1 数据预处理
设水资源承载力评价指标集为{x(i,j)|i=1,2,…,n;j=1,2,…,m},对于指标值越大水资源承载力越大类指标,利用式(1)对评价指标进行处理;对于指标值越小水资源承载力越大类指标,利用式(2)进行处理。
(1)
(2)
式中:x(i,j)为指标特征值归一化序列;x*(i,j)为第i年第j个评价指标;xmax(j),xmin(j)分别为第j个评价指标的最大和最小值;n,m分别为评价区年度数量和评价指标数目。
3.1.2 投影指标函数及最大熵目标函数
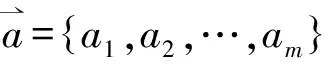

(3)
式中a为单位长度向量。
依据最大熵原理,熵值越大,意味着寻优获得的投影向量分布不确定性和随机性最小。为求出投影方向的最佳分布,可构建最大熵目标函数,即
(4)
式中:H(a)为最大熵;a2(j)表示各投影方向概率分布,反映各指标对一维综合值的影响程度,即可用a2(j)表示各指标权重值。
3.1.3 构造多准则优化目标函数
为使各评价区综合值的分布在整体上尽量分散、局部上尽量紧密,可根据综合值的类密度最大、类间距离最大为目标,构建式(5)多准则目标函数,将MEPP技术确定最优投影方向问题转化为非线性最优求解问题,即:
(5)
式中:Q(a)表示待优化目标函数最大值;Sz为投影值z(i)的标准差;Dz为投影值z(i)的局部密度。Sz和Dz表达式参见文献[15]。
3.1.4 计算投影值
3.2 混合蛙跳算法
混合蛙跳算法(SFLA)在各行业领域均有应用,算法通过模拟青蛙群体觅食时,按一定规则将蛙群划分为多个子群,各子群内部进行局部搜索,并对子群内部表现最差的青蛙个体进行更新,经过一定次数的独立进化后,各子群重新混合完成信息交流,并进行下一轮的进化,直至满足设定的收敛条件[16-19]。SFLA实现步骤可简述如下。
(1)随机生成P=NM只青蛙组成的初始群体,第i只青蛙个体表示为xi=(xi1,xi2,…,xiS)(i=1,2,…,P)。其中,S为解空间维度;M为子群数;N为子群内青蛙数量。计算每个青蛙个体初始适应度值f(xi),并按f(xi)降序排序,再将各青蛙个体逐一循环分配给M子群。
(2)在子群进化过程中,对每个子群中f(xi)最差的个体Fw按式(6)进行调整。
Fw,new=Fw,old+rand(0,1)·(Fb-Fw,old)。(6)
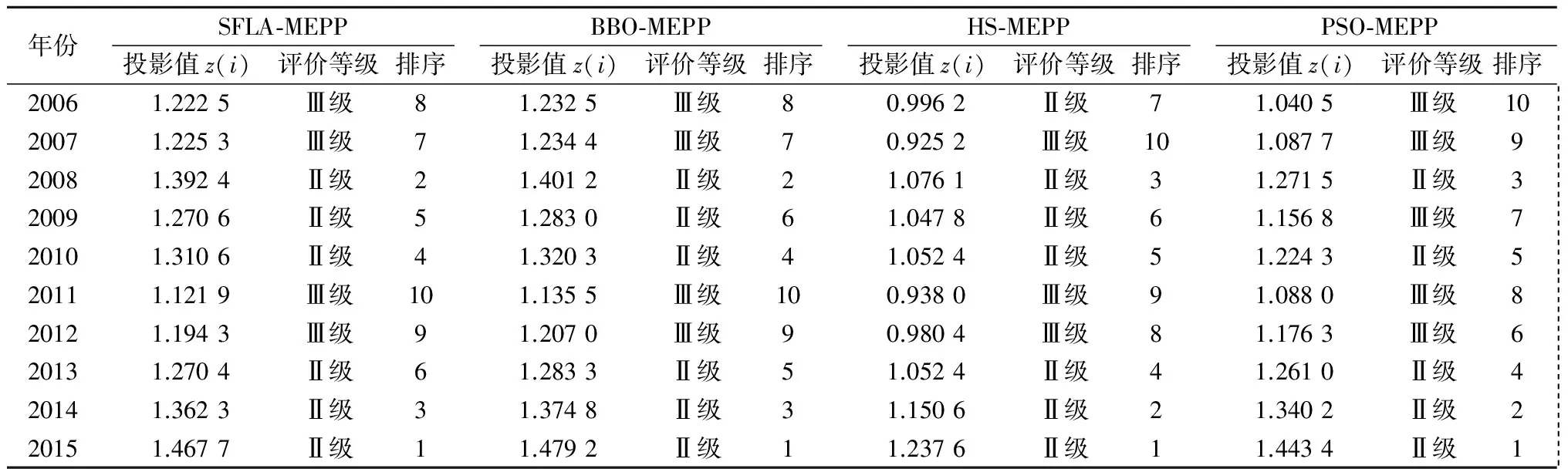
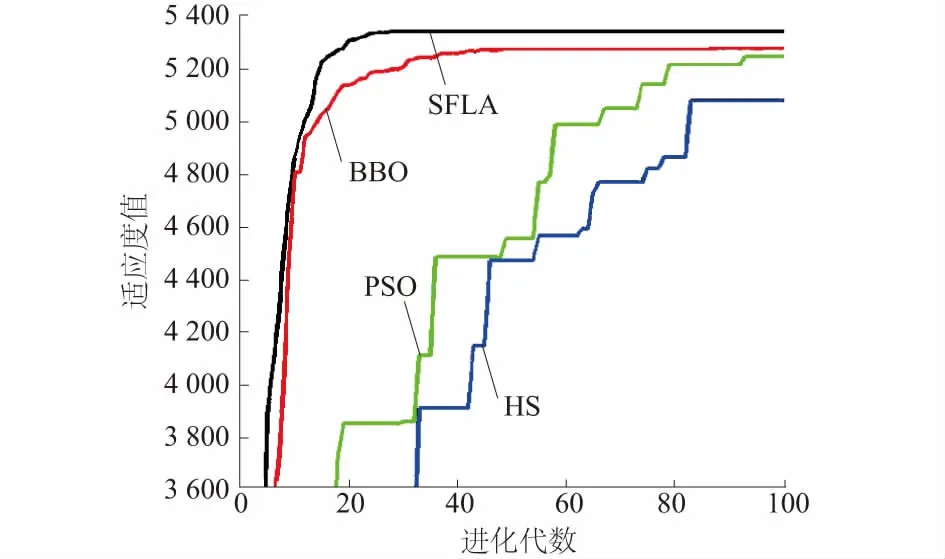
若f(Fw,new) Fw,new=Fw,old+rand(0,1)·(Fg-Fw,old)。(7) 若仍有f(Fw,new)≥f(Fw,old),则按式(8)进行局部搜索。 Fw,new=Fnew。 (8) 式中:Fw,new,Fw,old分别表示第k(k=1,2,…,M)个子群中最差个体更新的新旧值;Fb表示子群k中局部最优个体;Fg表示青蛙群体的全局最优个体;Fnew表示随机产生的新个体。 (3)对各子群重复局部搜索直至满足子群进化终止次数T1。 (4)将各子群中的P个青蛙个体混合进行全局信息交流,并按适应度值重新排序和划分子群;然后继续进行局部搜索。如此反复迭代直至满足算法终止条件或最大迭代次数T。 SFLA-MEPP水资源承载力评价实现步骤可归纳如下(其他3种算法可参考实现)。 (1)构建水资源承载力评价指标体系和分级标准;基于表1,在各分级标准阈值间随机生成样本,利用式(1)、式(2)对生成的样本进行一致性处理。 (2)确定多准则优化目标函数。利用随机生成的样本构建多准则优化目标函数,即以式(5)作为SFLA等4种算法优化的目标函数,即适应度函数。 (3)初始化算法参数。设置最大迭代次数T,青蛙群体规模P,子群数M,子群内青蛙个数N和子群数局部进化次数TM。 (4)适应度值计算。利用式(5)计算每个青蛙个体初始适应度值f(xi),并按f(xi)降序排序,再将各青蛙个体逐一循环分配给M子群。 (5) 利用式(6)—式(8)对每个子群中f(xi)最差的个体Fw进行调整或局部搜索。 (6)对各子群重复局部搜索直至满足子群进化终止次数TM;将各子群中的P个青蛙个体混合进行全局信息交流,并按适应度值重新排序和划分子群后进行局部搜索。 (7)判断算法是否满足终止条件。若满足,则转至步骤(6);否则重复步骤(4)—步骤(7)。 (10)利用z′(s)对云南省近10 a的水资源承载力进行评价及对比分析。 云南省地处我国西南边陲,辖昆明、曲靖、玉溪等16个州市。境内河流分属长江、珠江、红河、澜沧江、怒江、伊洛瓦底江6大水系。多年平均降水量1 278.8 mm,水资源总量2 210亿m3,约占全国水资源量的1/7,仅次于西藏、四川,居全国第3位;此外冰川雪山静贮水量约10亿m3,湖泊静贮水量近300亿m3,从邻近省区入境水量1 625亿m3,从缅甸、越南、老挝入境水量25亿m3,出境水量3 835亿m3,水资源总量相对丰富。近年来,随着云南省工业化、城镇化建设持续推进,水资源供需矛盾日益突出。据统计,2015年云南省用水量150.1亿m3,所辖部分州市用水总量已逼近甚至超出用水控制总量,万元工业增加值用水量66 m3/万元,农业用水量占年用水总量的69.7%,而生态环境用水量仅占1.56%,水功能区达标率为63.2%(28项指标评价),“三条红线”考核形势不容乐观。加之近10 a来,随着云南省经济社会快速发展、城镇化工业化进程加快,水资源供需矛盾日益加剧,水环境污染日趋严峻,水资源支撑经济社会可持续发展的要求越来越迫切,因此,科学客观评价近10 a来云南省水资源承载力,对于实现水资源可持续利用,实行最严格水资源管理制度,推进全面建成小康社会和水生态文明建设具有重要意义。 本文以2006—2015年云南省水资源承载力评价为研究对象,指标数据来源于《2015年云南省水资源公报》、《2015年云南省统计年鉴》等,见表2。 表2 云南省2006—2015年水资源承载力评价指标数据Table 2 Data of indicators of water resources carrying capacity in Yunnan Province from 2006 to 2015 注:各评价指标单位参见表1 表3 目标函数优化结果及比较Table 3 Comparison of optimization result among different algorithms 4.2.1 算法参数设置 SLFA最大迭代次数T=100,青蛙群体规模P=50,子群数M=5,子群内青蛙个数N=10,子群数局部进化次数TM=10。BBO算法最大迭代次数T=100,种群规模P=50,最大迁入率I=1,最大迁出率E=1,突变概率ms=0.1。HS算法最大迭代次数T=500,和声记忆库大小HMS=50,记忆库取值概率HMCR=0.95,音调微调概率PAR=0.3,微调步长bw=0.2。PSO算法最大迭代次数T=100,种群规模P=50,惯性权重ω=0.729,局部学习因子、全局学习因子c1=c2=2.0,个体速度取值范围为[-0.5,0.5]。4种算法搜索空间均设置为[-1,1],维度均为14维。 4.2.2 样本数据构造 基于表1,在各评价指标的每个分级标准阈值间随机生成10组样本,4个等级共随机生成40组样本数据,用式(1)及式(2)对生成的样本进行一致处理。 4.2.3 模型求解 4.2.4 综合投影值计算 表4 区域水资源承载力评价等级标准z′(s)Table 4 Rating criteria z′(s) of regional water resourcescarrying capacity obtained by different models 表5 云南省水资源承载力投影值z(i)及评价排序结果Table 5 Projection values z(i) of water resources carrying capacity and ranking of evaluation results 4.2.5 进化过程图绘制 4种算法某次进化过程见图1。其中,适应度值越大,表示其所对应的MEPP模型投影方向越佳。 图1 4种算法某次进化过程Fig.1 An evolutionary process by each algorithm 从表3—表5及图1可以看出如下结果。 (3)SFLA-MEPP模型对云南省近10 a水资源承载力评价结果与BBO-MEPP模型相同,但在排序上有2个存在差异;与HS-MEPP和PSO-MEPP模型在评价等级上有1个不同,在排序上均有9个存在差异。 (4)从表4、表5来看,SFLA-MEPP模型对云南省2006—2007年、2011—2012年水资源承载力评价为Ⅲ级,即“基本可承载”;其他年份评价为Ⅱ级,即“可承载”。从表5来看,云南省水资源承载力综合投影值z(i)出现先升(2006—2008年)、后降(2009—2012年)、再升(2013—2015年)的变化趋势,采用Spearman统计量|T|与Kendall统计量|M|对2006—2015年云南省水资源承载力综合投影值z′(i)进行分析。经计算,综合投影值z(i)的Spearman统计量|T|与Kendall统计量|M|分别为0.831和1.16,均小于置信水平为0.05时的相应临界值2.01和1.96,表明云南省水资源承载力随时间呈提升趋势,但提升趋势不显著。云南省近10 a水资源承载力出现振荡变化主要是受2009—2011年云南省3 a连旱的影响,以及在水功能区达标率、万元GDP用水量、农均灌溉用水量等指标上表现较差所导致。针对制约云南省水资源承载力水平提升的经济社会系统指标和生态系统指标,“十三五”期间,通过以下措施方法,云南省水资源承载力还有进一步提升的空间:一是加强工业、农业节水改造力度,提高用水效率;二是加大水环境治理投入,改善水环境质量;三是兴建水源工程,提高供水保证率。但由于受水资源系统随机变化以及人口增长、经济规模扩大、水源工程建设条件等因素的制约,云南省水资源承载力提升的空间十分有限。 (1)遵行可量化、可操作、指标可获取等原则,从水资源系统、经济社会系统、生态系统3个方面选取14个指标构建水资源承载力评价指标体系和分级标准,并在指标分级标准阈值间随机生成样本用于构建多准则目标函数。指标体系、分级标准及样本生成方法对于相关评价及研究具有一定的参考意义。 (2)利用SFLA寻优最大熵投影寻踪(MEPP)技术最佳投影方向,提出SFLA-MEPP水资源承载力评价模型,并构建BBO-MEPP、HS-MEPP和PSO-MEPP水资源承载力评价模型作对比,以云南省2006—2015年水资源承载力评价为例进行实例研究。结果显示:SFLA-MEPP模型对云南省2006—2007年、2011—2012年水资源承载力评价为“基本可承载”,其他年份评价为“可承载”;SFLA-MEPP模型对云南省水资源承载力评价结果与BBO-MEPP模型相同,但在排序上存在差异;与HS-MEPP和PSO-MEPP模型在评价结果及排序上均存在差异。验证表明,将SFLA-MEPP模型应用于水资源承载力评价是可行和有效的。 (3)SFLA优化多准则目标函数所获得的最优值、最劣值、平均值和标准差均优于BBO、HS和PSO算法,验证了SFLA具有较高的求解精度。从实例验证来看,对于MEPP技术,决定水资源承载力评价精度的关键因素是智能算法的极值寻优能力。 (4)从实例分析来看,云南省近10 a水资源承载力随时间呈提升趋势,但提升趋势不显著。通过实施工、农业节水改造,水环境整治,水源兴建等工程,云南省水资源承载力可以进一步得到提升,但受水资源系统随机不确定性变化、经济社会规模增长等因素的制约,云南省水资源承载力提升的空间十分有限。 参考文献: [1] 任 黎,杨金艳,相欣奕.江苏沿海地区水资源承载力研究——以盐城市为例[J].水利经济,2015,33(5): 1-3. [2] 雷艳娇,葛 强. 云南省地市(州)水资源承载力模糊综合评判[J].人民珠江, 2016, 37(4): 21-24. [3] 童纪新,顾 希.基于主成分分析的南京市水资源承载力研究[J].水资源与水工程学报,2015,26(1):122-125. [4] 宋桢桢, 顾银鲁.基于AHP法对宁夏水资源承载力的评价[J]. 哈尔滨师范大学自然科学学报, 2015,31(1):60-62. [5] 陈南祥,陈可飞. 基于物元分析法的水资源承载力评价方法研究[J].人民黄河, 2010, 32(8): 71-72,75. [6] 何慧爽.基于集对分析的中原经济区水资源承载力评价[J]. 人民黄河, 2014, 36(6): 75-77. [7] 郭晓英,陈兴伟,陈 莹,等.基于粗糙集和BP 神经网络组合法的水资源承载力动态变化分析[J].南水北调与水利科技, 2015,13(2):236-240. [8] 王淑娟.基于投影寻踪模型和加速遗传算法的石羊河流域水资源承载力综合评价[J].地下水,2009,31(6):82-84. [9] 吴雪梅,塔西甫拉提·特依拜,买买提·沙吾提,等.基于PSO-PPE模型的和田水资源承载力评价研究[J].干旱地区农业研究,2014,32(2):228-233. [10] 张 明,王贵作,张寅熙.水文相似流域最大熵优选模型研究[J].水利水电技术,2012,43(2):14-16,21. [11] 周念清,杨 硕,朱 勍.承载指数与模糊识别评价许昌市水资源承载力[J].水资源保护,2014,30(6):31-34. [12] 吴永斌.基于可拓理论的区域水资源承载力评价[J].水资源与水工程学报,2012,23(5):162-165. [13] 姜秋香,董 鹤,付 强,等. 基于SD 模型的城市水资源承载力动态仿真——以佳木斯市为例[J].南水北调与水利科技,2015,13(5):827-831. [14] 黄健元,金广宇,于彦博.投影寻踪模型在行蓄洪区运用风险评价中的应用[J].水利经济,2016,34(5):60-63. [15] 崔东文.鸡群优化算法-投影寻踪洪旱灾害评估模型[J].水利水电科技进展,2016,36(2):16-23. [16] 雷梦婷. SFLA-PP模型在区域水资源利用效率综合评价中的应用[J]. 长江科学院院报, 2017, 34(11): 27-32. [17] 张桂珠,胥 枫,赵 芳,等.一种具有领导机制的混合蛙跳优化算法[J].计算机应用研究,2014,31(7):1984-1988. [18] 王安龙,何建华,张 越,等. 基于伪差分扰动的混合蛙跳算法研究[J].计算机应用研究,2014,31(9):2681-2684. [19] 赵鹏军,邵泽军.一种新的改进的混合蛙跳算法[J].计算机工程与应用,2012,48(8):48-50.3.3 SFLA-MEPP水资源承载力评价实现步骤

4 实例应用
4.1 研究区概况

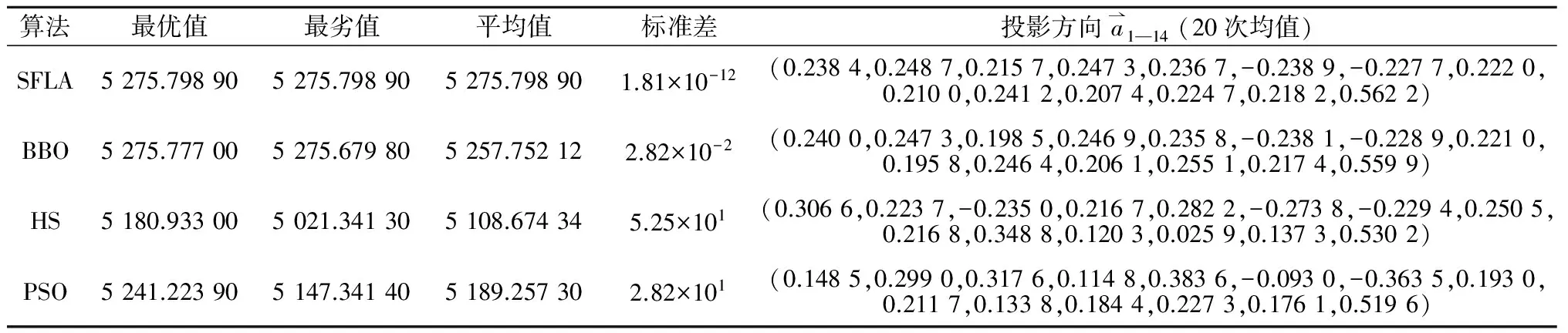
4.2 水资源承载力评价模型求解


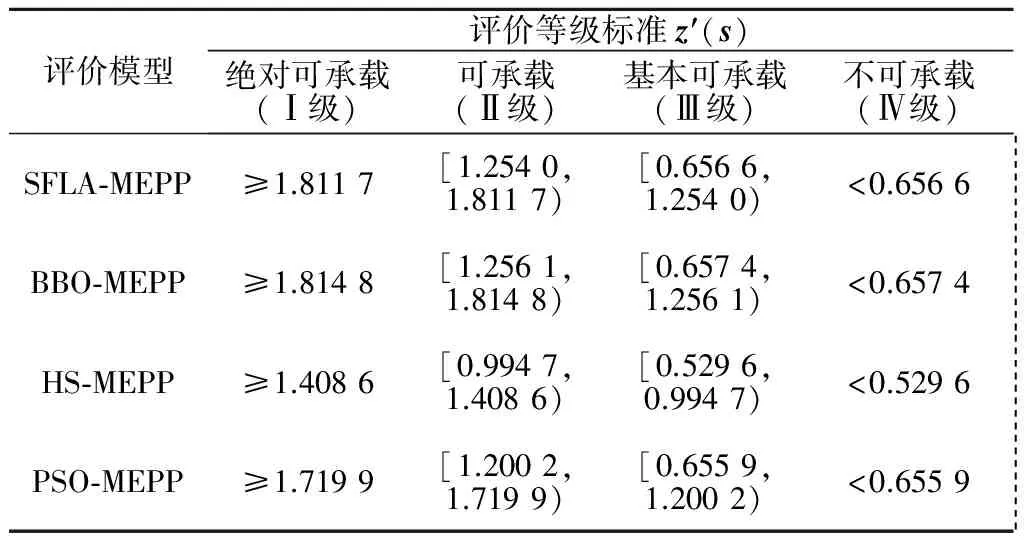
4.3 评价结果分析

5 结 论

