砖石古塔结构振动台试验模型设计与试验验证

李涛 王社良 杨涛

摘要： 为了得到小雁塔的动力特性，考虑结构特点与试验条件，对小雁塔砖石结构进行了振动台试验模型设计。基于结构动力相似基本方程，运用一致相似率和单参数畸变相似理论，对灰砖与砂浆进行了相似设计；采用欠人工质量模型，对配重进行设计，并对地震波的选取与调整进行了分析；对试验模型制作过程中某些细节的简化进行了阐述。通过对试验现象与前3阶动力特征值的对比分析，结果表明，采用所选的振动台试验模型，能够反映小雁塔结构的动力特性，也验证了试验模型的合理性。

关键词： 砖石结构； 振动台试验； 地震波； 相似理论

中图分类号：TU365； TU317+.1文献标志码： A文章编号： 1004-4523（2018）02-0314-09

DOI：10.16385/j.cnki.issn.1004-4523.2018.02.015

引言

砖石古塔承载着中华民族五千年的悠久文化，在中国的古代建筑历史上占据着极为重要的地位，是历史的见证和地震研究的重要资源。但因地震的破坏、材料的老化及自然的侵蚀，使古塔结构出现了不同程度的损伤，对现存的古塔结构进行研究就成为了亟待解决的问题[1-2]。但过往的专家学者多数是基于古塔结构的某一特性进行分析与评估[3-5]，缺乏对古塔整体结构系统的研究。伴随着计算机控制技术与结构动力学理论的发展，合理运用相似理论，建立振动台试验模型，真实还原古塔结构的震损受力性能，已成为国内外专家学者研究的焦点。

Chayanon Hansapinyo[6]对泰国的清迈双龙寺砖结构体系进行了动力性能测试，并与有限元模拟结果进行了双比分析；Donato Abruzzese[7]对上海淞江区护珠塔的动力性能进行了试验研究，并对古塔的破坏进行了风险评估。高大峰[8]对西安城墙永宁门箭楼进行了1∶6的局部缩尺振动台试验，分析了模型结构在不同强度地震激励下的动力反应与动力特性；赵祥、王社良[9]根据广州某古塔的主要受力和变形特点，设置了3种形状记忆合金阻尼器，并对安装了阻尼器的古塔结构进行了振动台试验，以验证阻尼器的设置对古塔结构抗震性能的提高程度；任德宇、李胜才[10]对四川龙护舍利塔进行了振动台试验，研究了地震损伤对结构动力特性的影响。

小雁塔位于西安市碑林区，因其宝贵的文物價值与研究价值，一直以来都是专家学者重点研究对象。早在上个世纪末，西安建筑科技大学的陈平、赵冬就已经开始对小雁塔的抗震能力进行研究[11]；2010年，利用石膏制作模型，进行了振动台动力测试，然后又对小雁塔的抗震风险评估进行了研究[12]。由于试验条件限制与相似理论的缺失，过往的文献缺乏对模型建立的系统阐述，因此文中基于动力方程与相似理论，对小雁塔1/10缩尺的振动台试验模型建立过程及简化措施进行阐述，旨在为小雁塔修复及类似的古塔振动台测试提供理论依据。

1试验初始数据〖2〗1.1小雁塔小雁塔建造于唐朝，是密檐式古塔的代表之一，距今已1300多年历史，经受了上千年风雨侵蚀和人为及自然灾害的摧残，外表和内部结构已有不同程度的破坏，虽然各个朝代对塔进行过多次修复和加固，但因技术能力有限未对塔体本身的贯通裂缝进行很好的加固修复，使其抗震性能不断降低，亟需进行抗震保护。

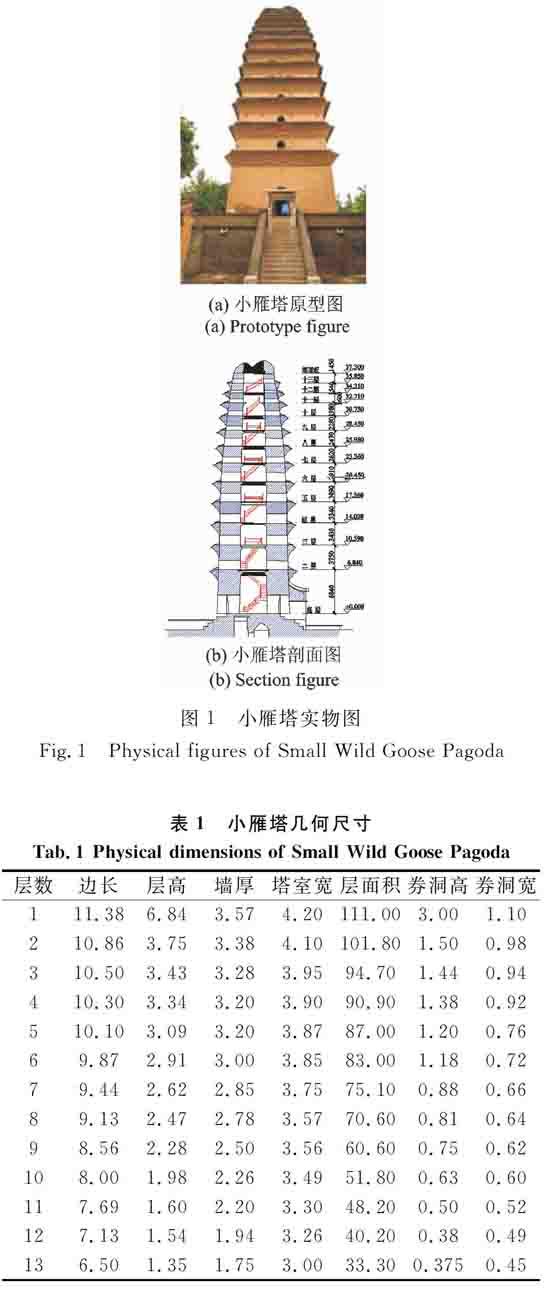
小雁塔底面为四边形，坐落于砖基上，塔身13层，残高43.3 m，底面边长11.38 m，二层以上高宽逐层递减内收，采用尺寸360 mm×180 mm×70 mm灰砖，塔檐处所用的灰砖尺寸较小，均用橙黄泥灰浆砌筑，单壁较厚成筒体结构，塔内部中空，在楼板处采用加强措施，有楼梯可以登顶[13]，其实物图如图1所示，几何尺寸如表1所示。

图1小雁塔实物图

Fig.1Physical figures of Small Wild Goose Pagoda

第2期李涛，等：砖石古塔结构振动台试验模型设计与试验验证振 动 工 程 学 报第31卷表1小雁塔几何尺寸

Tab.1 Physical dimensions of Small Wild Goose Pagoda

层数边长层高墙厚塔室宽层面积券洞高券洞宽111.386.843.574.20111.003.001.10210.863.753.384.10101.801.500.98310.503.433.283.9594.701.440.94410.303.343.203.9090.901.380.92510.103.093.203.8787.001.200.7669.872.913.003.8583.001.180.7279.442.622.853.7575.100.880.6689.132.472.783.5770.600.810.6498.562.282.503.5660.600.750.62108.001.982.263.4951.800.630.60117.691.602.203.3048.200.500.52127.131.541.943.2640.200.380.49136.501.351.753.0033.300.3750.45

1.2振动台

试验采用的三维6自由度地震模拟振动台试验系统由美国MTS公司生产，位于西安建筑科技大学草堂校区，振动台系统的主要性能指标参数如表2所示。

表2振动台系统主要性能参数

Tab.2Main performance parameters of shaking table system

性能指标参数台面尺寸/m4.1×4.1最大负荷/t30最大偏心距/m≥0.6试验频率/Hz0.1～50最大加速度/g1.0，1.0，0.9最大速度/（cm·s-1）±100，±125，±80最大位移/cm±15，±25，±10最大倾覆弯矩/（t·m）80注：最大加速度、速度与位移均依次为X，Y，Z；其中X，Y为水平方向，Z为竖直方向。

1.3原型结构动力特性

采用INV3060A多通道动态数据采集仪、941-B型水平及垂向加速度传感器等设备对小雁塔原型结构进行了现场动力测试，测试仪器均通过了陕西省计量科学研究院的计量鉴定。在13层楼面处设置低频拾振器，并将其作为测试的基本参考点，其余测点沿高度方向从地面至塔顶均匀布置。采用北京东方振动研究所开发研制的DASP V10专业版数据采集与信号处理软件；测试结束后，利用DASP模态分析软件对结果进行分析计算。则其模态振型及动力特性如图2及表3所示。

图2前3阶振型图

Fig.2Vibration pattern of the first three orders

表3动力特性值

Tab.3Dynamic characteristic values

动力参数1阶2阶3阶频率/Hz1.4494.7626.667周期/s0.690.210.15阻尼比/%0.9122.2716.3902原型与模型材料

小雁塔的墙体由灰砖和砂浆砌筑而成，试验设计前采用SJY800B砂浆贯入仪与ZC4型砖回弹仪对塔身灰砖和砌筑砂浆进行了强度测定，如图3所示。

图3原型强度测试

Fig.3Prototype strength test

按照相关文献的要求[14-15]，在小雁塔内部的每一层处选择10个砖样，每个砖样选择10个测点进行回弹测试。考虑现场所测砖样的结构整体性，使结果相对偏大，因此砖强度采用文献[16]的研究成果：砖墙上所测的回弹值比单块砖用砖墩和杆加压得到的回弹值高4.0，也即现场灰砖所测回弹值减去4.0即得灰砖的实际回弹值，然后与文献[14]中砖强度等级对照，经过调整，最终确定小雁塔砖砌体的平均强度为MU10。由文献[15]可得，小雁塔结构砌体的弹性模量可根据如下公式计算E=370fmfm（1）式中fm为砌体的强度平均值，单位为MPa。

每层选取16个测点进行砂浆贯入试验，测点在水平灰缝上均匀分布，两点之间不小于240 mm。试验测得砂浆的平均贯入深度，最终取平均砂浆强度换算值为0.95 MPa。

考虑模型砌筑时的可操作性，尽量减小因材料差异而对结构性能的影响，经过对西安多处现存砖砌体的强度与弹性模量的综合试验与分析，最终选取上世纪50年代建筑青砖，经强度与弹性模量测定，与小雁塔原型材料相近。胶结材料采用黄土、生石灰与糯米桨按一定比例配合，其中黄土与生石灰的比例为1∶1，制作70.7 mm×70.7 mm×70.7 mm标准砂浆试块进行抗压强度测试，经多次试配，最终选取了试验所用的砂浆配合比例，经测定，其抗压强度值为1.16 MPa。模型所用材料如图4所示，糯米砂浆试块的破坏形态如图5所示。

图4模型材料

Fig.4Model materials

图5糯米灰浆试块试验过程

Fig.5Test procedure for test block of sticky rice mortar3模型相似设计〖2〗3.1相似基本原理振动台试验相似设计时，通常需要考虑长度L、力F与时间t，此时结构的惯性力是施加在结构上的主要荷载，则由结构动力学基本方程可得m（（t）+g（t）+c（t））+kx（t）=0 （2）按照方程分析法的基本要求，动力方程中各物理量应满足的相似条件为Sm（S+Sg）+ScS+SkSx=0（3）按照国家地震局工程力学研究员张敏政[17]的基本理论，根据量纲协调原理，可以得到：Sm=SpS3l， Sc=SσS3lSa （4）将式（4）代入式（3）可得SρS3l（Sa+Sa）+SES3lSaSlSa+SES2l=0 （5）经化简可以得到振动台试验相似设计的基本相似方程为SESρSaSl=1（6）在相似设计时，从基本方程中选取3个参数作为可控相似常数，然后再按照似量纲分析法推广确定其它的几何、材料、力学与动力特性等相似常数[18]，即可进行正常的配重设计与其他相似设计。

3.2配重设计

考虑到文中所选材料、试验条件、振动台参数及吊车起吊量，选取L，E，ρ为相似基本常数，即分别取Sl =1/10（整体长度）， SE =1， Sρ=1.试验采用文献[17]建立的一致相似率，则根据最初确定的Sl及Sρ，可以计算出模型结构的质量为：mm=mpS3lSρ（7）

ma=SES2lmp-mm（8）

mom=SES2lmop（9）式中mm，mp分別为模型与原型的质量；ma为模型中需设置的人工质量；mom，mop分别为模型与原型中非结构构件及可变荷载的质量。

由原型小雁塔结构的尺寸和材料密度可计算出mp =2700 t， mop =250 t，由式（7）可得， mm=2.7 t。试验模型采用钢筋混凝土底板与振动台台面固定，尺寸设计为：2.5 m×2.5 m×0.2 m，由此可得底板重为mb=3.2 t。考虑振动台的最大承载力为30 t，扣除模型底板质量和模型质量后，即30-3.2-2.7=24.1 t，可得到模型中人工质量合计的计算值不超过24.1 t。

（1）若采用完全人工质量模型，则：Sa =1，Sg=1，时间St= S0.5l=0.32，频率Sf = S-1t=3.125，则可得出质量之和为32.7 t > 30 t，因此，此人工质量下模型不能实现；

（2）若采用忽略重力模型，mm=2.7 t，mom= SE S3 lmop= 0.25 t，Sa= S-1l=10，St= Sl=0.1，Sf =S-1l=10。尽管小雁塔模型自重与计算活载质量之和为2.95 t，小于振动台的极限承载力，但计算重力效应仅仅只有实际重力效应的（2.95/31.2）×100%=9.46%。重力效应过小，误差太大，试验结果不能反映结构原型的动力反应，因此，忽略重力模型也不可取；

（3）基于此，本次试验选用欠人工质量模型。由式（7），（8）和（9）可得，欠人工质量模型中人工质量的最大值为：ma=30-mm-mom-mb =21.6 t。然而考虑试验模型实际空间的大小，最终计算模型内部能够施加的最大配重质量为：ma=7.95 t。

3.3相似比设计

因每一层面积较小，忽略模型中活载与非结构构件的质量。此时，由牛顿第二定律（F=ma）可得，要想使试验模型产生的总惯性力不变，在人工质量不足的情况下，必须增加输入地震波的加速度峰值，以减小试验误差。因此，结合一致相似率，可以得到采用欠人工质量模型振动台相似常数如表4所示。

表4振动台试验相似关系

Tab.4Similarity relation of shaking table test

相似物理量相似关系式相似数值长度S10.1面积SA=S2l0.01应变Sc=Sσ/SE1弹性模量SE1应力Sa=SE1等效密度S=mm+ma+mqmL3r（mp+mop）3.61阻尼Sc=S2lS0.30.018时间St=SlS0.50.19频率Sf=S-1lS-0.55.26位移Sl0.1速度Sv=S-0.50.526加速度Sa=S-1lS-12.774地震波选取及调整

小雁塔位于西安市碑林区，场地类别为Ⅱ类，地震分组为一组，抗震设防烈度为8度，设计基本地震加速度值为0.20g，特征周期为0.35 s。选取加速度作为地震强度的控制指标，采用拟合设计反应谱法，按照规范[19]要求选取了3条有代表性的地震记录作为模型的水平输入：El-centro波（0.3417g）、汶川波（0.6273g）与上海人工合成波。将所选地震波峰值调整为多遇地震设计反应谱值（70 cm/s2），做阻尼为5%的反应谱分析，并与小雁塔所在场地的多遇地震设计反应谱进行比对，作为选波与输入顺序的依据，如图6所示。图6地震波反应谱与设计反应谱

Fig.6Response spectra of input ground motions and designed response spectrum

当结构处于基本周期（T=1.449 s）时，可得反应谱包络图不超过设计反应谱的20%，因此，所选3种波是合理的。而输入波的顺序则按结构周期对应点的反应谱数值大小进行排序，也即输入顺序为El-Centro波、汶川波与上海人工合成波。

对于原型结构，将3条地震波的峰值加速度（PGA）调整至0.2g，用以代表小雁塔所处场地（8度抗震设防烈度）的基本峰值加速度值[20]，调整后的地震波加速度时程如图7所示。对于缩尺结构模型而言，基于St=0.19， Sa=2.77，将每一条地震波的时间轴均调整为原型的0.19倍，将峰值加速度（PGA）则调整为原型的2.77倍（接近0.6g），用调整后的加速度时程曲线来模拟原型结构的基本抗震设防烈度下的峰值加速度值。经过缩比之后，3条地震波的时程都相对较短，尤其是El-centro波，在短短的几秒内就将会出现加速度的峰值，这对振动测试系统及数据采集装置来说都是一个挑战。因此，一方面，测试系统需要保证顺利的输入调整波；另一方面，需要提高数据采集系统的采样频率，并将采集到的数据进行滤波处理。

由于采用的是欠人工质量模型，试验时，还需要以增加加速度峰值的方法来弥补由于结构质量的缺失而导致的重力效应与惯性效应的不足。因此，试验中初步选定的加速度峰值为0.1g，0.2g，0.4g，0.6g与0.9g，其中，0.9g为八度大震下经调幅后的地震波强度基准值。在试验时，当每一次改变加速度峰值时，均在试验前后输入加速度峰值为0.05g的白噪音扫频，以获得结构每一工况下的自振频率。

图7原型调整后加速度时程曲线

Fig.7Acceleration time history curve after prototype adjustment

5试验模型简化设计

小雁塔平面呈方形，规则对称，南北方向上开有相互连通的门洞与窗洞，整体坐落在砖基上；塔身采用逐层递减的收分技术成锥体形（如图1所示）。为了方便实验制作及加载，忽略对试验结果影响较小的因素，对试验模型进行了简化，具体措施如下：

（1）底座的有效简化。小雁塔历经多次地震，塔身开裂严重，但却屹立不倒，与小雁塔的坚固基底密不可分。勘察资料显示，小雁塔的地基呈半球体，具有“不倒翁”的思想，场地条件和地基处理都是良好的，与周围的土层能够完美的形成一個整体[21]。因此，试验制作过程中，将下部用钢筋混凝土底板代替，与砖墙通过连接键可靠的连接，近似等价于固定端来处理。

（2）砖与灰缝的处理。若严格按照相似理论，试验模型用砖的尺寸过小，灰缝厚度也仅为1 mm，将使砌筑结构尺寸效应影响放大，粘结缺陷变大。因此，此处采用单参数畸变相似理论[22]，即结构的整体尺寸严格按照1/10采用，灰砖相似比取用1/3，灰缝采用1/2，以减少砂浆处的缺陷，且保证灰砖与砂浆能够可靠的接触，使两者能够共同工作，砖样与砂浆分别如图4与如图8所示。图8灰缝的处理

Fig.8Treatment of mortar joint

（3）配重的施加。因小雁塔结构的特殊性，原型结构的楼层分隔处没有设置楼板，只在四周设置加强措施，无法用常规振动台方法将配重搁置在楼板上。因此，在配重施加时，选择用预埋件和钢框架将其稳固地吊挂在墙壁上，以减小因振动过程中的相对碰撞对试验结果的影响，且在下部分散均匀布置。因上部的层高较小，为了施工的可操作性，将上部配重隔层布置，如图9所示。图9配重设计

Fig.9Counterweight design

（4）地震波的输入。由于小雁塔平面呈方形，截面对称，南北方向上开有券洞。地震波沿平面输入时，忽略南北与东西两方向上模型刚度的差异，仅仅沿相对弱侧（东西方向）输入地震波激励，南北方向的地震效应等同于东西方向（事实上，南北侧的震害要比东西侧的轻）。

经理论分析与试验设计，最终模型如图10所示。

图10小雁塔模型图

Fig.10Model of Small Wild Goose Pagoda6试验结果

经过对试验模型的地震波激励，可以得到主要的破坏特征如下：（1）试验过程中，随着地震波峰值加速度（PGA）的增加，由于“鞭鞘效应”的存在，小雁塔的塔顶摆动最为强烈，上部最先开始破坏；（2）局部券洞墙体都出现了横向和竖向裂缝和不同程度的破坏，且模型南北面墙体破坏程度比东西面更为严重，主要是由于在南北面墙壁上开洞使墙体的刚度减小，出现了应力集中现象，使得整个结构在这一层的抗剪强度明显减弱，洞口处易于开裂，是结构中的薄弱部位；（3）随着地震峰值加速度的增大，可以看到试验模型底层和底座出现了剥离的现象，塔脚部发生破坏，部分灰砖发生破碎，主要是因为小雁塔塔体本身重心较高，在水平荷载作用下容易发生失稳现象，这也说明了小雁塔底层和地基连接处也是结构的薄弱环节，需要重点保护。这种破坏模式和小雁塔实际破坏特征相似，模型典型的破坏模式如图11与12所示。

当地震波加速度改变时，对模型进行0.05g白噪声扫频。利用半功率带宽法[23]可以计算出结构的阻尼比，对时程曲线进行滤波与快速傅里叶变换，可以得到结构的频率。通过对模型前3阶频率与小雁塔原型结构现场动力测试对比，模型试验的周期比、频率比与阻尼比分别经相似比向原型结构反向转化；再以原型动力特性实测值为基准（表3）进行误差分析，如表5所示。图110.4g后模型底层局部裂缝分布

Fig.11Local crack distribution in 0.4g model of the first floor图120.6g后模型局部裂缝分布

Fig.12Model local crack distribution after 0.6g

表5模型试验与动力测试特征值对比

Tab.5Comparison of characteristic values between model test and dynamic test

阶次周期频率阻尼模型误差/%模型误差/%模型/%误差/%10.14510.236.897-9.510.015-8.6320.0437.1523.256-7.770.044-7.6230.0318.0132.258-8.780.119-3.45

由表5可知，模态分析中，模型经相似比转化后的动力特性与小雁塔原形结构动力测试结果间存在着差异。模型结构变化最大的是一阶周期，比原型结构增加了10.23%，究其原因，一方面由于模型结构内部空间的限制，将配重集中施加，造成了局部刚度的突变，致使周期变长；另一方面，基于单参数畸变相似理论，灰缝的刚度在模型整体刚度中所占的比例增大，而灰缝的刚度相对较小，从而造成了整体刚度的削弱，使周期在某种程度上变长。但整体来说，简化后的模型能够满足工程实际允许的误差要求，也说明了小雁塔模型设计的合理性，能够直观的反映出原型结构的动力特性。

今后在类似砖石古建振动台模型设计中，如何将配重均匀的布置，避免刚度的变化对动力特性的影响，就成为了制约砖石古建振动台试验精度的主要因素。

7结论

经过对小雁塔原型的动力测试及模型的振动台试验结果的对比分析，可以得到以下结论：

（1）以原型實测强度为基准的选材方式是可行的，利用一定配合比的糯米灰砖与上世纪的建筑青砖制作的模型，在某种程度上能够正确地反映砖石古塔结构的动力性能；

（2）欠人工质量模型与单参数畸变相似理论在古塔的振动台试验模型设计中是可取的，但配重的施加要尽量能够真实地反映现实结构，以减少对模型结构刚度的影响；

（3）地震波的选取要以场地的特征周期为基准，并按照不同的地震波持时与加速度峰值进行调整，最终才能作为激励波输入；

（4）对试验模型的简化要合理、有效，以减小试验误差，在增加试验模型制作的可操作性的同时，保证动力特性测试的可信度。

参考文献：

[1]陈平，贠作义，宋泽维.砖石古塔的地震风险评估[J].工业建筑，2015，45（4）：98—102.

Chen Ping， Yun Zuoyi， Song Zewei. Earthquake risk assessment of ancient masonry tower[J].Industrial Construction， 2015，45（4）：98—102.

[2]卢俊龙.实心砖石古塔动力特性与结构操作分析[J].力学与实践，2016，38（5）：560—566.

Lu Junlong. Damage and dynamic characteristics analysis of a solid structure pagoda[J].Mechanics in Engineering， 2016，38（5）：560—566.

[3]芦苇，赵冬，王玉兰.基础刚度对砖石古塔地震响应影响研究[J].地震工程学报，2016，38（4）： 498—503.

Lu Wei， Zhao Dong， Wang Yulan. Impact of foundation stiffness on the seismic response of ancient masonry pagoda[J]. China Earthquake Engineering Journal， 2016，38（4）： 498—503.

[4]袁建力.砖石古塔基本周期的简化计算方法[J].地震工程与工程振动，2015，35（2）：151—156.

Yuan Jianli. A simplified method for calculating the fundamental period of ancient masonry pagodas[J]. Earthquake Engineering and Engineering Dynamics， 2015，35（2）：151—156.

[5]劉红彪，李宏男.地震模拟振动台试验模型相似设计中的材料弹性模量取值问题研究[J].振动与冲击，2016， 35（3）： 114—120.

Liu Hong-biao， Li Hong-nan. Evaluation method for material elastic modulus in the similitude design in structural shaking table test[J]. Journal of Vibration and Shock， 2016， 35（3）： 114—120.

[6]Chayanon Hansapinyo， Nakhorn Poovarodom. Ambient vibration tests and finite element analysis for dynamic properties of brick masonry inverted bell-shaped chedi[C].ICCEN 2013，2013：212—216.

[7]Donato Abruzzese，Lorenzo Miccoli，Jianli Yuan. Mechanical behavior of leaning masonry Huzhu Pagoda[J]. Journal of Cultural Heritage，2009：，10（4）：480—486.

[8]高大峰，刘静，李飞，等.西安城墙永宁门箭楼振动台试验研究[J].地震工程与工程振动. 2014，34（5）： 140—149.

Gao Dafeng， Liu Jing， Li Fei， et al. The researches on shaking table test of Yongning Gate embrasure watch-tower of Xi′an city wall[J]. Earthquake Engineering and Engineering Dynamics， 2014，34（5）： 140—149.

[9]赵祥，王社良，周福霖，等.基于SMA阻尼器的古塔模型结构振动台试验研究[J].振动与冲击，2011，30（11）： 219—223.

Zhao Xiang， Wang She-liang， Zhou Fu-lin， et al. Shaking table tests for ancient pagoda model structure based on shape memory alloy actuating devices[J]. Journal of Vibration and Shock， 2011，30（11）：219—223.

[10]任德宇，李胜才.地震损伤对砖塔动力特性影响的小型振动台试验研究[D].扬州：扬州大学，2015.

Ren De-yu， Li Sheng-cai. Small-capacity Shaking Table Test on the Influence of Seismic Damage on the Dynamic Behavior of Masonry Pagoda[D]. Yangzhou： Yangzhou University，2015.

[11]陈平，赵冬，姚谦峰.西安小雁塔抗震能力探讨[J].西安建筑科技大学学报，1999， 31（2）： 149—151.

Chen Ping， Zhao Dong， Yao Qianfeng. An exploration of the seismic behavior of Xi′an Xiaoyan Pagoda[J]. Journal of Xi′an University of Architecture and Technology， 1999， 31（2）： 149—151.

[12]沈远戈，陈平，赵冬.小雁塔抗震性能分析及地基构造研究[D].西安：西安建筑科技大学， 2010.

Shen Yuange， Chen Ping， Zhao Dong. Seismic behavior analysis and foundation construction research on Xiaoyan Pagoda[D].Xi′an： Xi'an University of Architecture And Technology，2010.

[13]樵卫新.荐福寺与小雁塔[M].西安： 陕西人民出版社，2002.

Qiao Weixin. Temple of Blessing and Small Wild Goose Pagoda[M]. Xi′an： Shanxi People′s Publishing House，2002.

[14]中华人民共和国工业和信息化部.回弹仪评定烧结普通砖强度等级的方法（JCT796-2013）[S].北京： 中国建材工业出版社，2013.

Ministry of Industry and Information Technology of the Peoples Republic of China. The method of evaluation the fired common brick strength grading by rebound hammer（JCT796-2013）[S]. Beijing： China Building Material Industry Publishing House，2013.

[15]Indirli M，Castellano M G，Clemente P，et al. Demo-application of shape memory alloy devices：the rehabilitation of the S.Giorgio Church Bell Tower[J].Smart Structures and Materials， 2001， 4330（5）：262—272.

[16]陈纪萱，靳康邮.回弹法测定墙体上砖的标号及超声法评定砖墙砌筑质量的研究[J].建筑技术，1996，（02）： 122—124.

Chen Jixuan，Jin Kangyou. Determination of the brick on the wall by rebound method and the evaluation of brick masonry quality by ultrasonic method[J]. Architecture Technology， 1996，（02）： 122—124.

[17]张敏政.地震模拟实验中相似律应用的若干问题[J].地震工程与工程振动，1997，17（2）： 52—58.

Zhang Min-zheng. Study on similitude laws for shaking table tests[J]. Earthquake Engineering and Engineering Dynamics， 1997，17（2）： 52—58.

[18]周颖，吕西林.建筑结构振动台模型试验方法与技术[M]. 第2版. 北京：科学出版社，2016.

Zhou Ying， Lü Xilin. Method and Technology for Shaking Table Model Test of Building Structures[M]. 2nd ed. Beijing： Science Press，2016.

[19]中華人民共和国住房和城乡建设部.建筑抗震设计规范[S].北京：中国建筑工业出版社， 2010.

Ministry of Housing and Urban-Rural Construction of the People's Republic of China. Code for seismic of buildings[S].Beijing： China Building Material Industry Publishing House，2010.

[20]金玉龙，吴天行.集装箱码头岸桥结构的动力相似分析与试验验证[J].上海交通大学学报，2012，46（10）： 1609—1615.

Jin Yu-long， Wu Tianxing. Dynamic similarity analysis and experimental verification on a quayside container crane[J]. Journal of Shanghai Jiaotong University， 2012，46（10）： 1609—1615.

[21]高大峰. 小雁塔塔体抗震、抗风性能及其地基极限承载力探讨[D]. 西安：西安交通大学，1995.

Gao Dafeng. The Characteristics on combat earthquake and wind of the small wild Goose Pagoda′s construction and the study of the foundation limit strength[D]. Xi′an：Xi′an Jiaotong University，1995.

[22]李哲，胡吉全，王东.地震载荷作用下岸桥结构单参数畸变相似模型研究[J].振动与冲击，2014， 33（20）： 164—169.

Li Zhe， Hu Jiquan， Wang Dong. Distortion model of container cranes subjected to seismic load[J]. Journal of Vibration and Shock， 2014，33（20）：164—169.

[23]应怀憔. 波形和频谱分析与随机数据处理[M].北京：中国铁道出版社，1983.

Ying Huaiqiao. Waveform and Spectrum Analysis and Random Data Processing[M]. Beijing： China Railway Publishing House，1983.

Design and experimental verification of shaking table test model

of brick masonry structure in ancient pagoda

LI Tao1，2， WANG She-liang1， YANG Tao3

（1.School of Civil Engineering， Xi′an University of Architecture and Technology， Xi′an 710055， China；

2.College of Urban， Rural Planning and Architectural Engineering， Shangluo University， Shangluo 726000， China；

3.School of Environmental and Chemical Engineering， Xi′an Polytechnic University， Xi′an 710048， China）

Abstract： In order to measure the dynamic characteristics of the Small Wild Goose Pagoda， a shaking table test model of the brick masonry structure is designed considering the structure characteristics and the experimental conditions. Based on the basic equation of structural dynamic similarity， the similarity design of grey brick and mortar is carried out by using the theory of uniform similarity and single parameter distortion similarity. The additional weight is designed by using the artificial mass model， and the selection and adjustment of seismic wave are analyzed. Finally， the simplification of some details is expounded. Through comparing the test failure and dynamic eigenvalues of the first three order modes， the test results show that the shaking table test model in this paper can reflect the dynamic characteristics of the structure and verify the rationality of the experimental model.

Key words： brick masonry structure； shaking table test； seismic wave； similarity theory