双参平面内单级直齿圆柱齿轮系统动力特性综合分析

田亚平 褚衍东 饶晓波

摘要： 为揭示非线性直齿圆柱齿轮系统分岔、啮合冲击、脱啮和动载系数间的耦合关系，在时变啮合刚度幅值系数与无量纲频率参数平面内用PNF法和延续算法对单级齿轮系统的动力学模型求解获其周期/冲击、脱啮占空比、齿背啮合比、动载系数伪彩图。研究表明：幅值系数和频率是影响分岔、冲击、脱啮、动载系数的主要因素，随幅值系数递增系统经倍化、Hopf、激变、擦切、鞍结分岔方式由周期运动通向混沌，并导致啮合冲击、脱啮占空比和动载系数增大；混沌、拟周期运动和啮合冲击现象出现在共振频率附近，其脱啮、动载系数在该处出现极值。双参平面内综合动力特性转迁规律为齿轮结构设计参数优化提供理论参考。

关键词： 非线性振动； 单级齿轮传动系统； 动力特性； PNF数值法； 双参平面

中图分类号： O322； TH132.425文献标志码： A文章编号： 1004-4523（2018）02-0219-07

DOI：10.16385/j.cnki.issn.1004-4523.2018.02.004

引 言

齿轮传动广泛应用于各类机械装置中，其非线性动力学行为是影响齿轮疲劳寿命的主要因素。Kahraman等[1]考虑齿侧间隙和误差激励因素建立了单自由度单级齿轮系统动力学模型，发现了次谐响应和混沌响应。Vinayak等[2]研究了齿轮啮合综合传递误差对系统非线性动力学行为的影响。刘晓宁[3]等用增量谐波平衡法对三自由度齿轮系统周期运动进行分析并判稳。苟向锋[4]用相图、Lyapnuov指数谱、Poincaré截面法找出了三自由度单级齿轮副随参数变化通向混沌运动的途径。王晓笋[5]等研究了含磨损故障的单级齿轮传动系统的分岔行为及通向混沌的途径。

PNF法（Poincaré-Newton-Floquet）是一种结合Floquet稳定性理论的周期运动求解、判稳同步进行的高效数值方法。PNF法在非线性动力学方面获得了大量研究成果。罗跃纲[6]研究含裂纹和碰磨耦合故障的转子系统周期运动的稳定性问题，韩清凯[7-8]研究碰磨转子系统的周期运动稳定性问题，李同杰[9]研究行星齿轮传动系统周期运动的稳定性问题，杨振 [10] 等研究正交面齿轮传动系统分岔特性，田亚平[11]等研究了单级齿轮系统的周期运动及稳定性问题。上述成果均是单参下系统的分岔特性及周期运动稳定性问题，无法全面了解多参数耦合对系统动力特性的影响。双参平面內研究非线性动力特性能理清系统参数之间的耦合关系并确定稳定运行的参数范围，为实际工程中齿轮机构的参数选择提供理论指导。苟向锋等[12-13]采用胞映射和逃逸算法研究了双参平面内纯扭转齿轮副的分岔特性和齿轮-转子系统扭转振动系统的周期运动及分岔特点。但综合运用PNF法和延续算法研究齿轮系统在双参平面内综合动力特性（分岔、啮合冲击、脱啮及动载系数）的文献还鲜有报道。

本文以单级直齿圆柱齿轮系统的动力学模型为研究对象，用PNF法和延续算法对系统的周期运动、分岔、啮合冲击、脱啮及动载系数进行求解，获得时变啮合刚度幅值系数和无量纲频率双参平面伪彩图，探寻其动力特性随参数转迁的规律和耦合匹配关系。

第2期田亚平，等： 双参平面内单级直齿圆柱齿轮系统动力特性综合分析振 动 工 程 学 报第31卷 1 单级直齿圆柱齿轮系统非线性动力学模型 单级直齿圆柱齿轮传动系统动力学模型如图1所示。图中，主从动齿轮的质量、转动惯量、基圆半径、扭转角位移和输入输出扭矩用mgi，Igi，rgi，θgi，Tgi（i=1，2）表示；主从动齿轮支承轴承的间隙、阻尼、线性刚度、作用于轴承的径向预载荷和径向位移用bi，cbi，kbi，Fbi，ygi表示。时变啮合刚度、齿侧间隙、啮合线性阻尼、综合误差用kh（t），2bh，ch，e（t）表示。

图1 单级直齿圆柱齿轮传动系统非线性模型

Fig.1 The nonlinear model of a single-stage spur gear system

定义无量纲齿轮啮合的动态传动误差与静态传动误差的差值y3

y3（τ）=[rg1θg1（τ）-rg2θg2（τ）+yg1-

yg2-e（τ）]/bc（1）

式中 bc为特征长度。

由文献[3]知其系统的无量纲动力学方程为

1=-fb1-2ζ111-2ζ133-k11f（y1，b1）-

k13（τ）f（y3，b3）

2=fb2-2ζ222+2ζ233-k22f（y2，b2）+

k23（τ）f（y3，b3）

3=fm+fah1Ω2cos（Ωτ）+1-2-2ζ333-

k33（τ）f（y3，b3）（2）

式中 yi（i=1，2）为轴承无量纲径向位移，yi=ygi/bc（i=1，2）；ζij（i，j=1，2，3）为阻尼比，ζij=cij/（2mijΩn），Ωn为系统固有频率，Ωn=km/me，km为啮合刚度平均值，me为啮合等效质量。fbi为无量纲轴承径向预载荷，fbi=Fbi/（mgiΩ2nbc）。fm为无量纲齿轮啮合平均激励力，fm=Tg1/（rb1meΩ2nbc）。fah1为无量纲内部激励动载系数， fah1=ea/（mebc）。k33（τ）=1+αcos（Ωτ），k13（τ）= k23（τ）= k33（τ）/4，α为啮合刚度幅值系数，Ω为无量纲频率，Ω=Ωh/Ωn，Ωh为啮频。Kii= Ω2bi/Ω2n， Ωbi为轴频，Ωbi=kbi/mgi。τ为无量纲时间，τ=Ωnt。f（yi，bi）为间隙非线性函数，bi=bhi/bc。f（yi，bi）=yi-bi，yi>bi

0，yi≤bi

yi+bi，yi<-bi（3）式中 bi为齿侧和轴承支承的无量纲间隙。

对系统（2）进行降阶处理，用状态变量{x1，x2，…，x6}替代y1，1，…，y3，3，则系统（2）的状态空间方程转化为

1=x2

2=-fb1-2ζ11x2-2ζ13x6-k11f（x1，b1）-

k13（τ）f（x5，b3）

3=x4

4=fb2-2ζ22x4+2ζ23x6-k22f（x3，b2）+

k23（τ）f（x5，b3）

5=x6

6=fm+fah1Ω2cos（Ωτ）+2-4-2ζ33x6-

k33（τ）f（x5，b3）（4）

2 动力特性分析参数〖*2〗2.1 脱啮占空比和齿背啮合比 由文献[14]知，齿轮啮合中存在无冲击、齿面擦切、脱啮单边冲击、齿背擦切和齿背啮合双边冲击，其冲击类型（impact=0，1，2）和脱啮状态由最小啮合综合误差xmin与齿侧间隙b来判断，其表达式为

impact=0，xmin>b无冲击，无脱啮

0，xmin=b齿面擦切，无脱啮

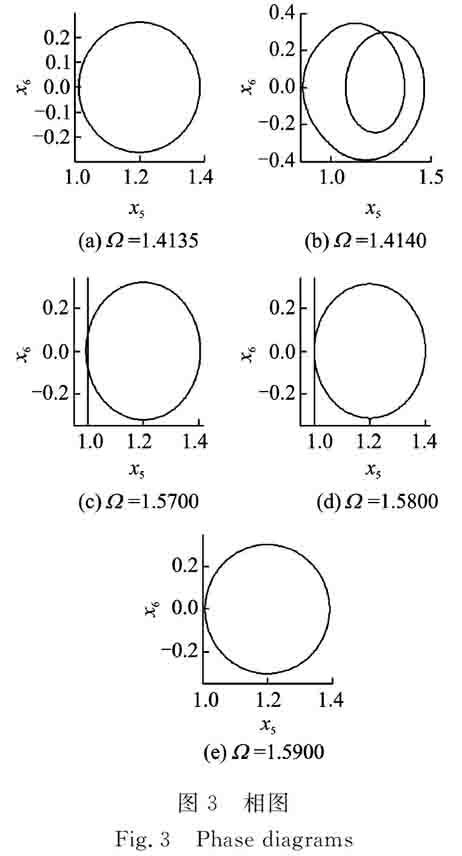
1，xmin

1，xmin=-b齿背擦切，脱啮

2，xmin<-b双边冲击，齿背接触 （5）

脱啮或齿背啮合下，齿面产生的拍击和附加动载荷是导致啮合状态恶化的主要因素。脱啮占空比和齿背啮合比用来表征齿轮脱啮状态恶化情况。设齿轮在一个啮合周期T内脱啮时间为t1，齿背啮合时间为t2，则脱啮占空比DC1和齿背啮合比DC2为DC1=t1/T

DC2=t2/T（6）2.2 動载系数

在齿轮强度计算中，为考虑齿轮振动导致啮合力增大的影响因数定义动载系数。动载系数受轴承刚度、齿轮箱结构、载荷状态、润滑剂等因素影响，其计算十分复杂，为了突出间隙和时变刚度对动载系数的影响，定义动载系数为周期内最大啮合力与平均啮合力的比值G=FdmaxFm=K（t）f（y3，b3）+C3Fmmax（7）式中 Fdmax为啮合周期内最大啮合力，Fm为平均啮合力，经无量纲化为DLC=（∑3i=1ki3（τ）f（x5，b3）+∑3i=1ζi3x6）/fmmax（8）3 系统非线性动力特性综合分析

在双参平面内，为分析系统（4）的非线性动力综合特性及其转迁规律，取仿真参数：ζ11=ζ22=0.02，ζ13=ζ23=0.0125，ζ33=0.05，k11=k22=1.25，fah1=0.05，fb1= fb2=0.1，b1=b2=0，b3=1，仿真初值均取为0。无量纲平均载荷fm的大小表征了齿轮系统载荷状态，本文中fm=0.2代表齿轮轻载运行状态。无量纲频率Ω∈[1，2]表征齿轮处于中高速运动状态。即仿真参数表征中高速轻载状态下齿轮系统动力学综合特性。

3.1 PNF法系统分岔类型的判别及追踪

PNF法分岔、追踪、判稳方法如下：

（1）以Ω为分岔参数，用PNF法[9-10]求解Ω0处的不动点X0及周期数P；

（2）用延续算法[15]以ΔΩ为步长，追踪Ω=Ω0+ΔΩ处的周期解不动点X；

（3）求解不动点转迁矩阵的最大Floquet乘子|λmax|，判断其|λmax|是否大于1，若|λmax|≥1转入步骤（4），否则转入步骤（2）；

（4）当|λmax|≥1时，系统发生了分岔，该点为分岔点，并由Floquet理论[16]判断分岔类型，停止该周期的延续追踪，以下一点为新起始点，转入步骤（1）重新求解周期和不动点；

（5）当遍历Ω参数区域结束追踪。

取α=0，Ω∈[1，2]的分岔图和判稳图如图2所示。图2Ⅰ分岔图表明：在参数区间内系统主要以周期1（P1，下同）运动存在，仅在Ω∈（1.414，1.502）内以P2运动形式存在。图2Ⅱ为|λmax|判稳图，最大Floquet乘子|λmax|从Ω=2开始以P1延续追踪，当Ω∈（1.414，1.502）时，P1运动失稳|λmax|>1，端点为分岔点。

考查其分岔点的Floquet乘子，并判别其分岔类型如表1所示。其Floquet乘子能准确地找出其分岔点和分岔类型，同时延续算法不需大量的瞬态求解，提高求解效率，故较Runge-Kutta法求解速度更快。

图2 PNF延续法分岔及判稳图

Fig.2 Bifurcation and stability diagram by PNF and continuation method

表1 基于PNF延续算法的系统分岔类型判别

Tab.1 Bifurcation type discriminant with PNF and continue method

考查点

（分岔点）参数 （Ω，α）追踪周期PFloquet乘子λ|λmax|分岔类型A（1.414，0.0）P1（0.1844±0.8971i，0.9203，0.5614，-1.0228，-0.8207）1.0228倍化B（1.502，0.0）P1（0.6663 ± 0.3062i，-0.0246 ± 0.9193i，-1.0032，-0.8359）1.0032倍化C（1.263，0.5）P1（1.6521，0.4259，0.9053，0.9053，0.7125，0.7750）1.6521鞍结D（1.337，0.2）P2（0.6564 ± 0.7573i，-0.3892 ± 0.7315i，0.1072 ± 0.3943i）1.0022HopfE（1.376，0.2）P2（1.8340，0.5643，0.5643，0.8331，0.8331，0.3020）1.8340鞍结

Floquet理论无法判断含间隙系统的擦切运动及擦切分岔现象，故在延续追踪中需按式（5）判断。图2Ⅰ中频率Ω的部分相图如图3所示。在分岔点A点前系统处于无冲击单周期运动（图3（a）），在分岔点A处不但发生了倍化分岔（图3（b）），且系统位移穿越非光滑点x5=1（x=b）截面发生了擦切分岔，故在分岔图上表现出了幅值跳跃现象。在Ω∈[1.570，1.590]区间内系统为稳定的P1运动，但系统经历了单边冲击（图3（c））、擦切运动（图3（d））和无冲击运动（图3（e））的转迁，因穿越x5=1截面时周期运动状态未改变，故在Ω=1.580处仅发生了擦切运动。

图3 相图

Fig.3 Phase diagrams图4 系统综合非线性动态特性图

Fig.4 Nonlinear dynamic characteristic graphs

3.2 频率Ω对系统综合动力特性影响

时变啮合刚度幅值系数α是表征齿轮啮合重合度大小，传动稳定性的主要指标；无量纲频率Ω是表征系统转速高低的主要指标。因此，选取参数α和Ω为分析对象。

取无量纲频率Ω为分岔参数，分别取α为0，0.2，0.5表示高、中和小重合度啮合状态，结合式（5），（6）和（8）计算出其系统动态传动误差x5随Ω变化的分岔、冲击、脱啮、动载系数等非线性特性如图4所示。

图4（a）为α=0的时不变刚度系统，系统经历了P1-P2-P1运动转迁形成周期泡分岔，在Ω=1.414和1.502处发生了倍化分岔（如表1所示）。在Ω∈（1.414，1.580）区间系统发生了脱啮单边冲击（impact=1，图4（a）Ⅲ），其脱啮占空比较小（DC1<0.22，图4（a）Ⅱ），受倍周期分岔的影响（Ω=1.502处）脱啮占空比发生了跳跃突变。无冲击（impact=0）状态下动载系数较小（1

图4（b）为α=0.2的小幅值时变刚度系统，系统经Hopf、鞍结激变、倍化分岔获得了P1-拟周期-P2-混沌-…-P4-P2-P1的运动状态。单边冲击区域扩大为Ω∈（1.310，1.722），脱啮现象加剧，脱啮占空比增大到0.6左右，动载系数增大到2.2左右，且在倍化分岔点Ω=1.515附近出现了极值。

图4（c）为α=0.5的大幅值时变刚度系统，系统经鞍结激变、Hopf、倍化分岔出现了P1-混沌-P2-混沌-P2-混沌-P1-混沌-P1的系统运动状态。单边冲击继续扩大到Ω∈（1.263，1.923），在Ω∈（1.250，1.317）区间出现了齿背啮合双边冲击（impact=2）和脱啮单边冲击（impact=1）的交替状态，最大DC1稳定在0.6附近，DLC稳定在2.2左右。

结合图4三种啮合刚度幅值系数α仿真结果表明：随α的递增系统的混沌、拟周期运动范围扩大，齿轮啮合单边冲击、脱啮占空比和动载系数递增，稳定周期运动的范围减少。α为常数时，随Ω变化系统的冲击特性、脱啮现象、动载系数随系统的拟周期或混沌运动而加剧。

3.3 （Ω，α）双参平面内综合动力特性分析

在（Ω，α）双参平面内研究系统的综合动力特性及其耦合转迁规律具有工程实际意义。图5（a）～（d）为系统的冲击/周期“I/P”、脱啮占空比“DC1”、齿背啮合比“DC2”和动载系数“DLC”动态特性伪彩图。

图5（a）伪彩图中，用不同的颜色区分不同的“I/P”运动 [17]，其区域的边界线即为分岔曲线。为突出短周期运动状态，对于周期数P≥65的周期运动、拟周期运动和混沌运动均用“I/n”表示。当系统从状态“0/P”向“1/P”状态转迁时，如周期运动未变则发生了擦切运动（G m），如周期运动发生了变化则产生了擦切分岔（G Bif）其交线为擦切曲线。当系统从“I/P”向“I/（2P）”转迁时发生了倍化分岔（PD Bif），其交线为倍化分岔曲线。系统的Hopf分岔（PF Bif）、鞍结分岔（SN bif）和激变分岔（CIC）由Floquet乘子判断。脱啮占空比DC1（图5（b）），齿背啮合比DC2（图5（c））和动载系数DLC（图5（d））灰度图中，对动力特性指标分级处理，并用不同的灰度值表示其脱啮、齿背啮合和动载系数程度。

图5 （Ω，α）双参平面内系统非线性动力学特性图

Fig.5 Nonlinear dynamic characteristic in the （Ω，α） two-parameter plane

在中高速轻载（Ω，α）∈（[1，2]，[0，0.5]）的双参平面内，系统表现出丰富的分岔/冲击特性，如图5（a）所示。平面内系统以P1运动为主，从Ω=1向Ω=1.4递增时，因齿面擦切和系统分岔点重合故在系统分岔点处伴随有擦切分岔而激变。随α递增系统出现了如下几种分岔现象：系统通过擦切、倍化方式通向“1/2”，“1/4”运动状态（α<0.0475）；系统通过擦切、Hopf、鞍结分岔方式通向混沌“1/n”运动（0.0475<α<0.1675）；系统通过鞍结、激变、擦切分岔方式进入混沌“1/n”运动（0.1675<α<0.5）。从Ω=2向Ω=1.4附近递减时，系统从“0/1”通过擦切运动转迁为“1/1”运动，后经倍化分岔通向混沌“1/n”运动状态。特别在（Ω，α）∈（[1.8，2.0]，[0.25，0.5]）区域内系统出现了周期3经鞍结分岔转迁为混沌，同时存在多处擦切激变分岔现象使“0/1”转迁为“1/n”，“1/3”，“1/8”等运动状态。在混沌区域内系统混沌状态出现了单边冲击混沌向双边冲击混沌转迁的现象，即在混沌状态下出现了内部吸引子激变（CIC）现象。沿α方向， “1/2”运动向混沌运动转迁过程中出现了自相似的叉式分支分形结构。

图5（b）的脱啮占空比（DC1∈（0，1））灰度图揭示了双参耦合下齿轮脱啮程度。结合图5（a），“0”表示无脱啮现象，出现在“0/1”运动区域；“0～0.1”表示出现了轻微脱啮冲击现象（00.6）。在各类分岔点处脱啮占空比发生了突变跳跃现象。

图5（c）的齿背接触啮合比（DC2∈（0，1））灰度图揭示了齿轮传动双边冲击齿背啮合的程度。結合图5（a）冲击/周期运动状态，在双边冲击混沌“2/n”运动区域内出现了齿背接触轻微冲击（0

圖5（d）为动载系数（DLC>1）灰度图，结合图5（a），“1～1.2”表示动载荷轻微波动（12.2）。

根据齿轮啮合原理，重合度越大（α越小），齿轮传动平稳性越好，动载荷波动越小。综合分析图5（a）～（d）中系统动力特性综合指标可得：时变刚度幅值系数是影响系统动力学的主要因素之一，系统动力学特性随幅值系数增大（重合度较小）而变差，系统的分岔和啮合冲击在线性共振频率（Ω=1.3～1.5）附近变得十分复杂，系统动力参数达到极值，仿真结果和工程实际基本吻合。因此在齿轮系统参数设计中通过增大重合度减小刚度幅值系数和调整结构参数避开共振频率是提高系统疲劳寿命的有效措施。在“0/1”区域内根据设备实际需要的动载系数选择参数区域为齿轮结构设计提供理论依据。

4 结 论

在时变啮合刚度幅值系数和无量纲频率双参平面内，用PNF延续算法对单级齿轮非线性系统进行数值求解获得了分岔、啮合冲击、齿背啮合、脱啮、动载系数伪彩图。通过分析获得如下结论：

1）综合运用PNF法和延续算法进行系统稳态周期解/分岔求解是一种高效、精确的数值方法。

2）时变啮合刚度幅值系数是影响齿轮周期运动分岔、脱啮、动载系数增大的主要因素之一。齿轮啮合综合特性随啮合刚度系数的增加（重合降低）而变差，直至系统混沌失稳，影响系统的疲劳寿命。

3）含间隙齿轮系统除了常见的倍化、Hopf、鞍结激变分岔外还存在擦切激变分岔，而分岔引起了系统动载系数、脱啮现象的阶跃突变。

4）系统共振频率和齿侧间隙所引起的分岔和啮合冲击是导致脱啮、动载系数突变的主要因素，在混沌区域其冲击和动载现象最剧烈达到极值。

5）在双参平面内的无冲击周期1运动“0/1”区域内选取动载系数参数是提高设备稳定性延长疲劳寿命的主要措施。

参考文献：

[1] Kahraman A， Singh R. Non-linear dynamics of a spur gear pair[J]. Journal of Sound and Vibration， 1990， 142（1）：49—75.

[2] Vinayak H， Singh R， Padmanabhan C. Linear dynamic analysis of multi-mesh transmissions containing external rigid gears [J]. Journal of Sound and Vibration， 1995，185（1）：1—32.

[3] 刘晓宁，王三民，沈允文. 三自由度齿轮传动系统的非线性振动分析[J]. 机械科学与技术， 2004，23（10）：59—61.

LIU Xiaoning， Wang Sanmin， SHEN Yunwen. Nonlinear vibrations of 3-DOF geared rotor-bearing system[J]. Mechanical Science and Technology for Aerospace Engineering， 2004，23 （10）：59—61.

[4] 苟向锋，陈代林.三自由度齿轮传动系统的分岔与混沌研究[J].机械科学与技术，2014，33（2）：199—203.

Gou Xiangfeng， Chen Dailin. Research on bifurcation and chaos of 3-DOF gear transmission system[J]. Mechanical Science and Technology for Aerospace Engineering， 2014，33（2）：199—203.

[5] 王晓笋， 巫世晶，周旭辉，等. 含磨损故障的齿轮传动系统非线性动力学特性[J]. 振动与冲击， 2013，3（16）：37—43，69.

Wang Xiaosun， Wu Shijing， Zhou Xuhui， et al. Nonlinear dynamics analysis of gear transmission system with wear fault [J]. Journal of Vibration and Shock， 2013， 3（16）：37—43，69.

[6] Luo Yuegang， Ren Zhaohui， Ma Hui. Stability of periodic motion on the rotor-bearing system with coupling faults of crack and rub-impact [J]. Journal of Mechanical Science and Technology， 2007， 21：860—864.

[7] Han Qingkai. Periodic motions of a dual-disk rotor system with rub-impact at fixed limiter [J]. Proc. JMSE， Part C： Journal of Mechanical Engineering Science， 2008， 222（C10）： 1935—1946.

[8] Han Qingkai. Periodic motion stability of a dual-disk rotor system with rub-impact at fixed limiter [J]. Vibro-Impact Dynamics of Ocean System， LANCM， 2009，44：105—109.

[9] 李同杰，朱如鵬，鲍和云，等. 行星齿轮传动系的周期运动及其稳定性[J].振动工程学报，2013，26（6）：815—822.

Li Tongjie， Zhu Rupeng， Bao Heyun， et al. coexisting periodic solutions and their stability of a nonlinear planetary gear train[J]. Journal of Vibration Engineering， 2013， 26（6）：815—822.

[10]杨 振，王三民，范叶森，等. 正交面齿轮传动系统分岔特性[J]. 哈尔滨工业大学学报，2011，43（3）：107—110.

Yang Zhen， Wang Sanmin， Fan Yesen， Liu Haixia. Bifurcation characteristics of face-gear transmission system[J]. Journal of Harbin Institute of Technology， 2011，43（3）：107—110.

[11]田亚平，褚衍东，饶晓波. 单级齿轮系统的周期运动及其稳定性[J]. 机械设计，2017，34（2）：45—49.

Tian Yaping， Chu Yandong， Rao Xiaobo. Periodic motion and its stability of a single-stage gear system [J]. Journal of Machine Design， 2017， 34（2）：45—49.

[12]Gou Xiangfeng， Zhu Lingyun， Chen Dailin. Bifurcation and chaos analysis of spur gear pair in two-parameter plane [J]. Nonlinear Dynamic， 2015， 79：2225—2235.

[13]苟向锋， 陈代林. 双参变量下齿轮-转子系统扭转振动特性分析[J].工程力学，2014，31（11）：211—217.

Guo Xiangfeng， Chen Dailin. Dynamic analysis on torsional vibration of gear-rotor system in two parameters plane[J]. Engineering Mechanics， 2014，31（11）：211—217.

[14]李润方， 王建军. 齿轮系统动力学-振动、冲击、噪声[M]. 北京：科学出版社， 1997.

Li Runfang， Wang Jianjun. Gear System Dynamics Vibration， Shock and Noise[M]. Beijing： Science Press， 1997.

[15]胡海岩. 应用非线性动力学[M]. 北京：航空工业出版社，2000.

Hu Haiyan. Application of Nonlinear Dynamics[M]. Beijing： Aviation Industry Press， 2000.

[16]韩清凯，于 涛，王德友，等. 故障转子系统的非线性振动分析与诊断方法[M]. 北京：科学出版社，2010.

Han Qingkai， Yu Tao， Wang Deyou， et al. The Nonlinear Rotor System Vibration AnalysIs and Fault Diagnosis Method[M]. Beijing： Science Press， 2010.

[17]Luo G W， Zhu X F， Shi Y Q. Dynamics of a two-degree-of freedom periodically-forced system with a rigid stop： diversity and evolution of periodic-impact motions[J]. Journal of Sound & Vibration， 2015，334：338—362.

Dynamic characteristic analysis of a single-stage spur gear system in

two-parameter plane

TIAN Ya-ping1， CHU Yan-dong1，2， RAO Xiao-bo1

（1.School of Mechatronic Engineering， Lanzhou Jiaotong University， Lanzhou 730070， China；

2.Key Laboratory of System Dynamics and Reliability of Rail Transport Equipment of Gansu Province，

Lanzhou Jiaotong University， Lanzhou 730070， China）

Abstract： In order to reveal the coupling relationship among bifurcation， gear meshing impact， tooth separation， tooth back-side contact and dynamic load coefficient （DLC） of the nonlinear gear system， the pseudo color maps of the meshing impact and period， duty cycle of the mesh apart （DC1）， duty cycle of the tooth back-side contact （DC2） and DLC for a single stage gear system are obtained by Poincaré-Newton-Fouquet （PNF） and the continuation numerical calculation method in the time-varying meshing stiffness amplitude coefficient （TVMSA） and dimensionless frequency two parameters plane. Research shows that the TVMSA and resonance frequency are main factors for bifurcation， gear meshing impact and DLC of the gear system. With the increase of TVMSA， the system's periodic motion turns to chaos by the way of period-doubling， Hopf， crisis， grazing， saddle node bifurcation and the DC1， DC2 and DLC increase. Meanwhile， the chaos， quasi periodic motion and meshing impact phenomenon appear near the resonant frequency， in which the DC1， DLC reach the extreme values. The dynamic characteristics transitions laws can provide the theoretical reference for the optimization of the gear structure parameter.

Key words： nonlinear vibration； single-stage spur gear system； dynamic characteristics； PNF method； two-parameter plane