三相永磁同步电机的无差拍直接转矩容错控制

刘加妮，李益华，陈长凯，陈 龙，叶诗婷

（1.长沙理工大学电气与信息工程学院，湖南长沙410114；2.湖南中新工程项目管理有限公司，长沙410000）

1 引言

电机的容错性是在汽车和航空等领域中的一个关键性能指标，提高电机的容错性可以提高系统的安全可靠性。目前电动机驱动系统的可靠性方案主要有两种：余度方案以及容错方案［1］。余度方案采用冗余思想，通过重复配置系统资源来满足系统高可靠性的要求，但系统利用率不高；容错方案主要从容错式电机本体［2-7］、驱动拓扑［8］以及容错控制算法［9-16］三个方面出发，切除故障相，保证系统在不对称状态下继续正常工作，因此大大提高了系统的利用率，但是对控制水平也大幅度提高，要求控制技术有非对称控制能力。

目前，国内外研究主要集中于大于三相的多相永磁容错电机及其容错控制算法，且对TP-PMSM的容错控制仅局限于驱动拓扑，例如三相四桥臂［17］和三相四开关容错控制［18］。多相容错电机本身具有较强容错能力再结合高性能的容错控制算法，整个系统具有强容错能力，提高了系统的可靠性和安全性。然而TP-PMSM本体不具备容错能力，虽驱动拓扑容错控制能保证电机故障后仍然运行，但不能获得满意的运行性能［17-18］，因此，需进一步研究其容错控制算法，提高系统的动静态性能和容错性。

本文旨在尽可能少地修改控制结构并减少由于容错能力而增加的额外计算负担，研究TP-PMSM的容错控制算法。直接转矩控制具有“天然的”容错性，并且已经成功应用于多相永磁容错电机［16］。传统PMSM直接转矩控制存在的磁链、转矩脉动大、开关频率不固定等问题，而结合无差拍控制形成的无差拍直接转矩控制（DB-DTC），不仅动态响应快，而且定子磁链和转矩的脉动小，具有良好的动静态性能［19］。因此，为了提高TP-PMSM的容错运行性能，本文结合其故障模型和DB-DTC，提出了无差拍直接转矩容错控制（DB-DTFTC），使电机在故障前后都能获得满意的动静态运行性能。

2 TP-PMSM驱动电路的容错拓扑结构

在TP-PMSM控制系统中，若其中某相发生故障，可以通过隔离故障元件，断开该相，并将电机定子绕组中性点与逆变器母线的或附加的逆变器支路的中性点连接起来，通过调整剩余两相电流大小与相位，从而保证电机故障前后旋转磁动势保持恒定，进而使得电机正常运行［20］。

如TP-PMSM绕组以星型连接无中线，若A相发生故障被断开，则剩余两相将形成串联单相电机，此时电机的合成磁动势为：

图1 TP-PMSM驱动电路的容错拓扑硬件配置

如图1所示，在TP-PMSM的控制系统中，根据系统故障的情况，由软件发出命令，进行系统的重构，隔开故障元件和断开故障相A，并将电机定子绕组中性点与逆变器母线的或附加的逆变器支路的中性点连接起来，且对剩余两相电流的相位和幅值做一些合理的调整，即可以使电机正常运行。

3 TP-PMSM的容错数学模型

3.1 TP-PMSM在三相静止坐标系的容错数学模型

假设A相发生故障被断开，那么定子侧的电压方程为：

或写成矩阵形式：

磁链方程为：

其中，UB，UC，iB，iC，φB，φC分别为 B、C 相的相电压、相电流和磁链；Rs是定子绕组电阻矩阵；Lss和Lms为定子绕组电感矩阵，而Mψr为折算到定子测的转子磁链幅值；θre为转子位置，P为极对数。

转矩方程为：

由式（7）可知，电磁转矩Te由电动机的基本电磁转矩和电动机d、q磁路不对称而产生的磁阻转矩两部分组成。

3.2 TP-PMSM在两相旋转坐标系的容错数学模型

利用变换矩阵［12］

可将TP-PMSM在三相静止坐标系的电压、磁链和转矩方程（4）-（7）转换到与转子磁通定向的两 相旋转坐标系dq。因此可得，TP-PMSM在A相故障情况下，以转子磁链定向的两相旋转坐标系dq中的电压、磁链和转矩方程：电压方程：

磁链方程：

转矩方程：

式中ωrm是转子角速度。由式（10）可知，TP-PMSM经变换矩阵得到两项旋转坐标系的电磁转矩就与正常运行时的电磁转矩方程相等。

由此可见，故障时TP-PMSM在两相旋转坐标系dq的电阻矩阵和电感矩阵比正常运行时的电阻矩阵和电感矩阵更加复杂。故障时的电阻矩阵和电感矩阵不仅包括常数项，而且还存在dq轴之间的正弦交叉耦合项。该正弦交叉耦合项与转子位置 θre相关［21］。

4 无差拍直接转矩容错控制策略

在TP-PMSM正常运行时，无差拍直接转矩控制利用TP-PMSM的离散状态方程，以电磁转矩和定子磁链幅值零误差为控制目标，直接计算出应施加在定子端的电压矢量，最后经空间矢量调制技术（Space Vector Module—SVM策略）得到开关信号，实现了电机的有效控制。其中，转矩和磁链控制环无需PI调节器，结构简单，开关频率恒定。DB-DTC不仅继承了传统DTC动态响应快的优点，而且极大程度上削弱定子磁链和转矩的脉动，具有良好的动静态性能。同时采用定子电流观测器预测下一周期的定子电流，消除控制系统时间周期上的误差，实现系统实时、精确地控制［19］。因此，在TP-PMSM故障运行时，即使电机仅有两相电流，无差拍直接转矩容错控制算法/能够产生合适的定子端的电压矢量。这个矢量是表示每一开关周期定子磁链的变化，应该能够在TPPMSM产生旋转磁场，以满足期望的气隙转矩和定子磁链。

4.1 转矩线性方程

如TP-PMSM故障运行时的两相旋转容错模型式（8）-（10）所示，因为电机绕组电阻矩阵和电感矩阵存在RsE和LlsE，所以电机转矩线性方程、定子磁链和电流观测器也变得更复杂，且显著增加控制单元计算负担。

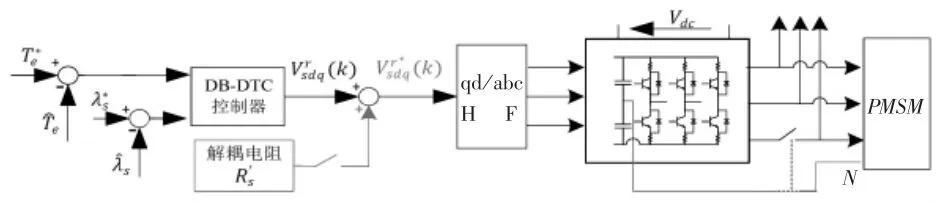
图2 驱动电路容错拓扑硬件配置和投入补偿电阻示意图

在无差拍直接转矩容错控制系统中，电机的期望电压指令对应无差拍控制器的输出加附加电压降△V。无差拍控制器输出是由TP-PMSM的容错模型中转矩方程（10）求导离散化确定的。先对式（10）求一次导：

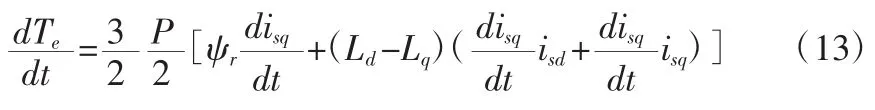
假设样本时间为Ts，将式（13）离散化：

将TP-PMSM的容错模型中电压方程（8）和磁链方程（9）联立，整理和离散化后，将式（14）代入便可以得出电机故障运行时的转矩线性方程（15）：

由式（15）可发现，该转矩线性方程与TP-PMSM正常运行时的转矩线性方程式是一样的。

同时电机定子磁链幅值满足：

然而，考虑功率转换器的直流母线电压给定的实际极限，只有一个Usd（k）值是可行的。将Usd（k）代入式（15）便可得到Usq（k）。

4.2 定子磁链观测器和电流观测器

与正常运行时一样，TP-PMSM故障运行时的定子磁链和电流可以用离散观测器估计，并且定子磁链和电流观测器故障前后不需做任何改变。定子磁链观测器采用加权系数的方式结合定子磁链观测器采用加权系数的方式结合“电流模型”和“电压模型”来估计定子磁链。因此，定子磁链观测器在低转速和高转速下都可以获得足够精确的定子磁链估计值。假设Lls＝0，RsE通过式（11）完全解耦，利用式（8）和式（9）可设计闭环观测器。图4给出了所使用的离散定子磁链观测器。因为对R＇s产生的电压降进行了补偿，所以正常运行时的定子磁链观测器数学模型也是适用的。

如图（3）所示，采用带有电压补偿的定子电流观测器可以获得零相位滞后磁链估计。它采用Luenberger观测器，能够根据采样电压和电流立刻估计在下一个采样周期的电流［22］。

图3 定子磁链观测器和电流观测器

图4 无差拍直接转矩容错控制框图

如图（4）所示，是 TP-PMSM 的 DB-DTFTC 框图。如图可知，电机的控制结构故障前后大体一致，使用相同的控制律和观测器。只是故障情况下，坐标转换矩阵不同和为了解耦R＇s引起的电压降进行了电压补偿。坐标变换矩阵集可以根据系统的状态选择：正常运行（H）和故障运行（F）。

5 无差拍直接转矩容错控制仿真

为了验证TP-PMSMDB-DTFTC的控制性能，在MATLAB/Simulink分别进行了TP-PMSM正常运行的无差拍直接转矩控制、A相断开带解耦的无差拍直接转矩容错控制和A相断开不带解耦的无差拍直接转矩容错控制，并对三种情形下的运行性能进行对比。试验中TP-PMSM参数见表1。

表1 TP-PMSM参数

仿真实验中，令负载转矩恒等于4Nm，转速为50rad/s（高速），在 0.5s转速变为 10rad/s（低速），在 1s转速又变回50rad/s。正常运行下的转子角速度ωrm、气隙转矩Te和定子相电流如图 5（a）。图 5（b）和图 5（c）分别给出了 A 相开路故障时带解耦和不带解耦的转子角速度ωrm、气隙转矩Te和定子相电流Iabc。在这三种情况下，电机速度都是可控的，且运动控制器的带宽为10Hz，定子电流观测器带宽为40Hz，磁链观测器带宽为10Hz。

图5 电机转子角速度ωrm、气隙转矩Te和定子相电流Iabc

从图 5（a）与图 5（b）可以看出，采用带解耦 DB-DCFTT的TP-PMSM在A相断开后，转速和转矩的运行性能与正常运行时相似，并且剩余两相电流幅值增加。此外，从图5（b）和图5（c）可以看出，采用不带解耦 DB-DTFTC 的 TPPMSM的转速和转矩在低速时有一定的纹波出现，电流不变，但电机仍然可以安全运行。

6 结论

本文在三相永磁同步电机（TP-PMSM）容错拓扑和断相故障模型基础上，结合无差拍直接转矩控制（DTC），提出了TP-PMSM无差拍直接转矩容错控制策略（DB-DTFTC）。该控制策略可使TP-PMSM发生故障后，在剩余两相电流下运行，并保持与正常运行时相同的动静态性能。

仿真结果表明，采用DB-DTFTC TP-PMSM即使在故障时，不仅动态响应快，而且极大程度地削弱了定子磁链和转矩的脉动，电流观测器能预测定子电流，大大提高了控制精度。因此，采用DB-DTFTC大大提高了TP-PMSM的运行可靠性和安全性。