基于风险博彩和比较静态分析视角的“大学生考试作弊”问题研究
李元丽
1 引言
大学生考试作弊行为在全国高校范围内广泛存在,中国青年报社会调查中心的调查结果显示:60.4%的受访者确认自己或周围同学在大学期间有过作弊行为[1]。不仅在中国,印度曾曝光父母充当蜘蛛侠帮助学生作弊以及学生集体要求作弊权的现象。大学生考试作弊问题也是学术界关注的焦点问题。李娜从课程的角度系统分析了高校学生考试作弊的原因,研究发现课程的重要性、课程的修读成本、课程的难度、考试设计以及教学质量都严重影响作弊行为产生[2];刘金铁等研究了大学生考试作弊影响因素研究,结果显示:教育体制、社会环境和个体行为是作弊行为的成因的前三名[3];张毅等通过调查问卷的方式分析了大学生考试作弊心理动机[4]。
从这些文献可以看出,现有的对大学生考试作弊的研究主要集中在大学生作弊的原因、心里动机和影响因素上,研究方法则以调查分析为主,研究的立足点都集中在如何治理作弊上。鲜有学者从经济学的角度研究大学生作弊问题。因此,从经济学角度研究大学生考试作弊问题具良好现实意义和理论价值。
2 基本假设和模型的构建
2.1 基本假设
1.大学生的唯一目标为最大化其预期效用并且独立决策,拥有的初始禀赋简化为0。
2.大学生的决策有两期,假设大学生是缺乏耐心的、短视的和慵懒的,主观贴现因子为β,0<β<1,并假设在期初决策的时候能准确预知到期末的决策。
3.在期初,大学生只有两种选择,一个是认真学习,假设期末必定能收获名义上的好处(比如获得课程通过,获得学分或者证书)N和实质性的好处(学到课程相关的知识、技能以及获得更好的工作机会或者继续深造的机会)M,但会损失闲暇L,假设M>N>L;另一个是不认真学习,假定肯定不能获得实质上的好处,也就是说认真学习是获得该门课程实质性知识和技能的唯一途径;同时由于实质性的好处要等到更长时间(如毕业工作以后)才能体现出来,因此假定M产生的效用需要更多期的贴现(简化成多一期)。
4.在期末,认真学习的大学生只有一个选择就是不作弊;不认真学习的学生有两个选择,一个是不作弊,假定肯定不会获得名义上的好处N,另一个是作弊,被抓的概率是P(可以被大学生在期初时准确预知),P与监考力度有关,被抓不但没有名义上的好处,还要受到处罚,处罚的损失为F,F>N,F与学校的处罚力度有关;不被抓就会获得名义上的好处N。
5. 学生的效用函数为具备期望效用函数性质的冯·诺依曼-摩根斯坦效应函数(即VNM效用函数)[6],记为v,v(0)=0,该效用函数是严格的增函数、严格的凹函数,且有连续的二阶导数。
6.以上所有参数均大于0。
2.2 基本模型的构建
认真学习是一个安全博彩(记为x),学生在期初损失闲暇L,期末无风险获得N和M,此时的效用为-v(L)+β*v(N)+β2*v(M)。
不认真学习有两种情况,一种是不作弊,是一个安全博彩,肯定获得0,效用为v(0);作弊是一个风险博彩(记为z),学生有1-P的概率获得N,有P的概率获得-F,此时的效用为P*[-β*v(F)]+(1-P)[β*v(N)]。
3 模型的求解
由于模型涉及到两期,期初的讨论主要是是否认真学习,期末的决策是是否作弊,所以模型的求解分为两个部分,先是关于是否作弊的讨论,再是是否认真学习的决策。
3.1 期末决策
定义一个N(P,F)给定监考力度和作弊处罚力度,作弊的效用等于不作弊时的效用,这个时候是否作弊对学生来说没有区别。则满足:
v(0)≡P*[-β*v(F)]
+(1-P)[β*v(N(P,F))]
(1)
又因为v(0)=0,所以上式等价于:
P*v(F)≡(1-P)v[N(P,F)]
(2)
(2)式左边是作弊的成本,(2)式右边是作弊的收益。当N=N(P,F)作弊和不作弊没有差别;当N>N(P,F),作弊的收益大于成本,学生会选择作弊;当N 1.比较静态分析 假定(2)式的解函数N(P,F)存在,则可对(2)式两边同时对P求导得: 同理对(1)式两边对F求导解得: 2.弹性分析 同理F对N的弹性为: 在期初决策时,由假设可知大学生已经知道的作弊被逮的概率预期值,该概率预期值可以通过以往的经验或者从高年级的学生口中得知。以0.5为分界线,分两种情况进行讨论。 1.P≥0.5 也就是作弊被抓的概率至少和不被抓的概率预期值相同。这时,由于F>N,P*v(F)>(1-P)v(N),出于理性的决策,学生一定会选择不作弊。这时决定学生是否认真学习的是-v(L)+β*v(N)+β2*v(M)与0的大小,由于M>N>L且v(·)单调增,则必然有:v(M)>v(N)>v(L)。显然可知-v(L)+β*v(N)+β2*v(M)>0的一个充分条件是:β2+β-1≥0,即β达到或者超过黄金分割点0.618,学生一定会选择认真学习的。 当β→0时,即使P值趋近于1即作弊一定会被抓,学生仍然会选择不学习,这是因为-v(L)+β*v(N)+β2*v(M)=-v(L)<-v(0)=0(注:v单调增且L>0)。 2.P<0.5且P*v(F)<(1-P)v(N) 选择认真学习的收益为-v(L)+β*v(N)+β2*v(M),不认真学习的收益为: P*[-β*v(F)]+(1-P)[β*v(N)]。两者相减得: β2*v(M)+P*β*[v(N)+v(F)]-v(L) (3) 当β→1时,即使P值趋近于0即作弊一定不会被抓,学生仍然会选择认真学习,因为这时β2*v(M)+P*β*[v(N)+v(F)]-v(L)=v(M)-v(L)>0。 4. 监考人员只要正常监考,作弊被抓和不被抓的概率相同,学生理性的选择都是不作弊。 6.当β→0时,即使P值趋近于1即作弊一定会被抓,学生仍然会选择不认真学习;当β→1时,即使P值趋近于0即作弊一定不会被抓,学生仍然会选择认真学习。 1.加强考生诚信教育,提高学生作弊的羞耻感,酌情对考试作弊的学生计入考试诚信档案,提高作弊的隐性成本。然而,有时候空洞的说教缺乏实效,再之诚信的收益在于长期,作弊的收益短期就能体现出来。为了避免诚信教育的空洞,对考试作弊的学生计入考试诚信档案就十分必要,一所大学四届之内只要有一人受此处罚,其震慑作用和教育意义将辐射整个校园以及后来的学弟学妹。 2.提高监考人员的责任心,增加作弊被发现的可能性(也就是提高P)。由结论可以知道,监考人员只要正常监考使得作弊被发现和不被发现的概率相等,大学生会做出不作弊的理性选择。但是在实际情况中,监考人员由于不作为或是出于“爱护学生”的目的,缺乏发现作弊的内在动力;同时很多高校管理人员认为发现考试作弊是考风、学风不正的表现而缺乏对监考人员的监管。因此,提高监考人员的责任心,增加作弊被发现的可能性是促使大学生认真学习的有效保证。 3.加强对考试作弊的惩处,以保证对于作弊的处罚要高于名义上的好处(F>N)。现在很多高校对作弊的惩处只是“逐出考场”或者该门成绩记零分,作为一个想作弊而通过考试的学生来讲,这样的处罚就是F=0的处罚,因为不作弊必然不通过,作弊却是有可能通过,那么作弊是必然的选择。而且学生之间的攀比,会出现“劣币驱逐良币”规律,选择作弊而不认真学习越来越多,选择不作弊而认真学习的人越来越少。因此,加强惩处力度是十分必要的。 4.提高主观贴现因子,克服短视。笔者认为短视是大学生考试作弊的主要原因,从结论中可以看出,主观贴现因子是影响学生是否认真学习的最关键因素。当主观贴现因子足够小时,即使考试一定会被抓,学生仍然会选择不认真学习;当主观贴现因子足够大时,即使考试一定不被抓,学生仍然会选择认真学习。因此,提高主观贴现因子,克服短视是解决大学生作弊问题重要手段。高校可以从以下几个方面做出努力:(1)更新办学理念,要把确实提高学生的素质和素养作为办学目标;(2)革新人才培养的评价体系:不能把就业率特别是初次就业率或者是就业数量作为评价办学好坏的指标;(3)改革各专业人才培养的方案,引导学生做一个着眼长远、脚踏实地和务实奋进的专业人才。 [参 考 文 献] [1] 张晴,熊旭. 调查称66.6%受访者认为大学生作弊现象普遍[EB/OL].[2015-06-19].http://edu.people.com.cn/n/2015/0619/c1053-27180916.html. [2] 李娜. 高校学生作弊的课程因素探析[J]. 中国考试,2013(12):58-64. [3] 刘金铁等. 高校学生考试作弊影响因素研究与分析[J].数学学习与研究,2015(08):32-34. [4] 张毅等. 高等工科院校学生考试作弊心理动机的研究[J].大学教育,2015(7):27-28. [5] 杰弗里·A·杰里,菲利普·J·瑞尼.高级微观经济理论[M].北京:中国人民大学出版社,2012:76-82.
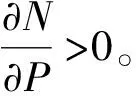
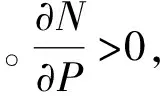


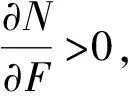
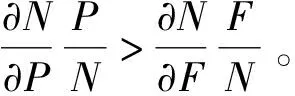
3.2 期初决策
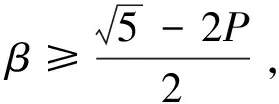
4 结论与建议
4.1 结论
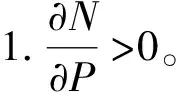
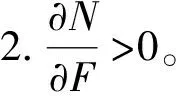
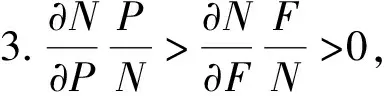
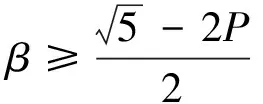
4.2 建议

