基于Multisim的RLC二阶动态电路的分析

管 飚

二阶动态电路的分析是《电路》本科课程中的重点和难点，也是培养学生电路分析能力的重要基础知识之一。但是，在大多数通用的教材中，主要是对RLC动态二阶电路进行简要的理论分析，而配套的实验设备基本是GLC并联电路，与教材的匹配不够完善。这样，学生很难直观地观察RLC二阶电路的实验效果，使得教学效果不够理想。本文在理论分析的基础上，通过Multisim软件对RLC二阶动态电路进行仿真，便于学生增加对RLC二阶电路的感性认识，全面地理解和掌握RLC二阶动态电路[1，2，3]。

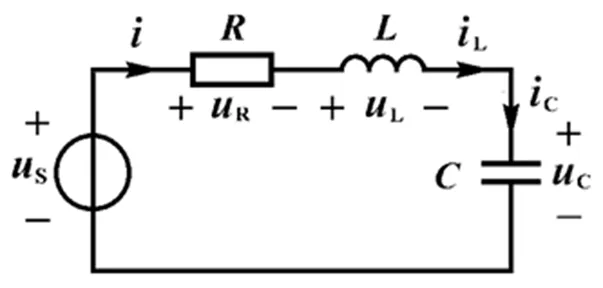
图1 RLC串联二阶电路原理图

如图1所示，电路中含有电阻和电感两个串联的动态储元件，据此电路建立的方程为二阶微分方程，常将这种电路称为RLC二阶串联电路。本文主要讨论电路中电容电压在零状态和零输入下的响应变化，以及电路中电容电压与电流的关系，这种关系也可以称为动态轨迹[4，5]。

1 二阶电路的理论分析

根据基尔霍夫电压定律[6]，由图1可得：

uR(t)+uL(t)+uC(t)=uS(t)

(1)

为了求出电容两端的电压，只需要求出电路中电感和电阻两端的电压，然后代入方程(1)。其中，由于是串联电路，那么流经三个元件的电流是相同的，即：

(2)

电阻和电感两端的电压分别为：

(3)

(4)

将上面两个表达式(3)和(4)代入方程(1)，可得如下的表达式：

(5)

方程(5)中，uS(t)是一个方波信号。在激励信号的前半周期，uS(t)=US，是零状态响应，方程(5)是一个二阶常系数非齐次线性微分方程。在激励信号的后半周期，uS(t)=0，是零输入响应，方程是二阶常系数齐次线性微分方程。方程(5)的特征方程为：

LCp2+RCp+1=0

(6)

方程(6)相应的特征根为：

(7)

特征方程的根，也称为电路的固有频率，从方程(7)可以看出，电路的固有频率只与电路中的电阻、电感和电容的参数有关，与输入信号无关。这样，通过更改电阻的阻值，就可以改变电路的固有频率。

在激励信号的前半周期，激励信号幅值为正，电容电压为零，这时二阶电路的响应是零状态响应，而在激励信号的后半周期，信号的幅值为零，电容电压不为零，这时，二阶电路的响应是零输入响应。在激励信号发生跳变时，二阶电路响应从一个稳定状态过渡到另一个稳定状态，这种过渡称为暂态过程，与电路本身的固有频率有关。根据特征方程根的不同，二阶电路的暂态过程可以分为欠阻尼、临界阻尼和过阻尼。根据方程(7)根号内算式的值，特征方程的根可以分为下列三类情况。

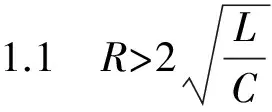
这时，p1和p2是两个不相等的实数根，微分方程的通解为：

uC(t)=A1ep1t+A2ep2t+uS(t)

(8)

只要求出A1和A2的值，就可以求出电容两边的电压。对方程两边求导数，可得：

(9)

在激励信号的前半个周期，t=0时，初始条件有uC=0，I0=0，uS=US，电路是零状态响应，方程(8)和(9)可简化为：

(10)

解方程组可得：

(11)

代入方程(8)后可以解得电容电压在零状态下的表达式：

(12)

在激励信号的后半个周期，t=0时，初始条件有uC=US，I0=0，uS=0，电路是零输入响应，方程(8)和(9)可以简化为：

(13)

解方程组可得：

(14)

代入方程(8)后可以解得电容电压在零输入时的响应：

(15)

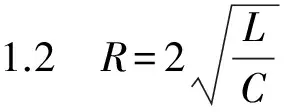
这时p1和p2是两个相等的实数根，微分方程(5)的解有如下形式：

uC(t)=(A1+A2t)ept+uS(t)

(16)

对方程(16)两边求导数，可以得到：

(17)

同样，在激励信号的前半个周期，t=0时，初始条件有uC=0，I0=0，uS=US，前两个方程可简化为：

(18)

解方程组后可以到：

(19)

将方程(19)代入方程(16)后可以得到电容电压在零状态下的响应方程：

uC(t)=US-USept(1-pt)

(20)

在激励信号的后半个周期，t=0时，初始条件有uC=US，I0=0，uS=0，方程(16)和(17)可以化简为：

(21)

解上面的方程组后可以到

(22)

计算结果(22)代入方程(16)后可以得到电容电压在零输入下的响应方程：

uC(t)=USept(1-pt)

(23)

这时，根号内的表达式为负数，p1和p2是一对共轭复数。

uC(t)=e-αt[A1cos(ωdt)+A2sin(ωdt)]+uS(t)

(24)

对方程(24)两边求导数，可以得到：

(25)

在前半个周期，t=0时，初始条件有uC=0，I0=0，uS=US，方程(24)和(25)可简化为：

(26)

解方程组后可以得到：

(27)

计算结果代入方程(24)后可以得到电容电压在零状态下的响应方程：

(28)

在后半个周期，t=0时，初始条件有uC=US，I0=0，uS=0，方程(24)和(25)可简化为：

(29)

解方程组(29)，可以得到：

(30)

计算结果代入方程(24)后可以得到电容电压在零输入下的响应方程：

(31)

2 RLC二阶电路的Multisim软件仿真

Multisim是美国国家仪器有限公司推出的一款仿真软件，适用于板级的模拟和数字电路的设计工作，使用者可以交互式地构建电路原理图，并对电路进行仿真，因此非常适合于电路基础的实验教学任务。本文使用NI Multisim v 10作为仿真工具。

根据上一小节的计论，电路的仿真也同样分为三个部分，每一部分给出了电容电压的响应变化，即暂态过程，以及电容电压随电流的变化轨迹，即状态轨迹。

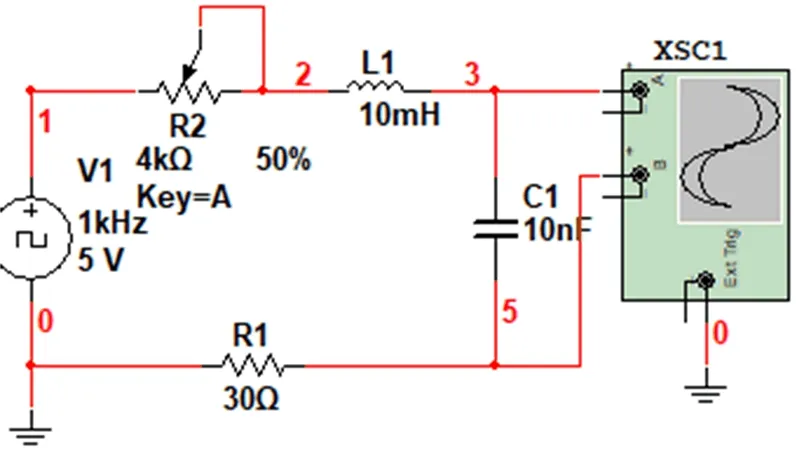
图2 实验电路图

实验用电路图如图2所示。示波器的通道A端接在电容的两端，用于显示电容两端电压的响应变化。为了显示电容电压与电路中电流的关系，就需要在示波器上显示出电流量。但是，由于双踪示波器只能用于观察电压量，因此，需要接入一个较小的电阻R1，作用是将电流量转化为电压量，便于示波器的观测，接在示波器的通道B端。

取R2=4.0kΩ，方程(6)有两个不相等的实数根，RLC电路过渡的性质为过阻尼的非振荡过程，图3显示的是电容电压在过阻尼状态下的暂态过程，图4显示的是电容电压在过阻尼状态下与电流的关系。

图3 过阻尼状态暂态过程

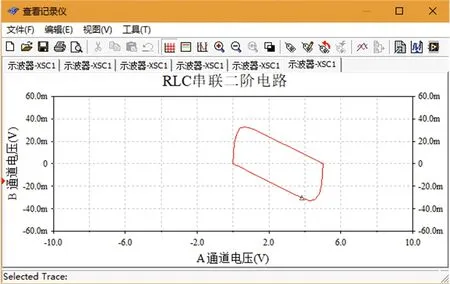
图4 过阻尼状态轨迹

根据电路图2，取R2=2.0kΩ，方程(6)有两个相等的实数根，这时，RLC电路的过渡性质为临界阻尼的非振荡过程。图5显示的是电容电压在临界阻尼状态下的暂态过程，图6显示的是电容电压在临界阻尼状态下与电流的关系。

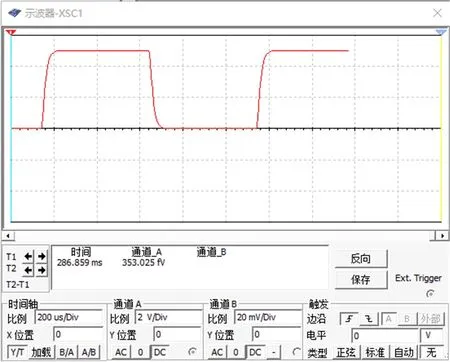
图5 临界阻尼状态暂态过程

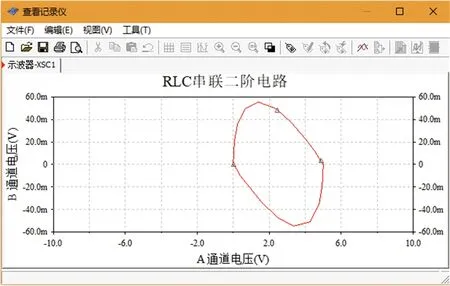
图6 临界阻尼状态轨迹

根据电路图2，取R2=0.4kΩ，方程(6)有两个不相等的复数根，这时，RLC电路的过渡性质为欠阻尼的振荡过程。图7显示的是电容电压在欠阻尼状态下的暂态过程，图8显示的是电容电压在欠阻尼状态下与电流的关系。

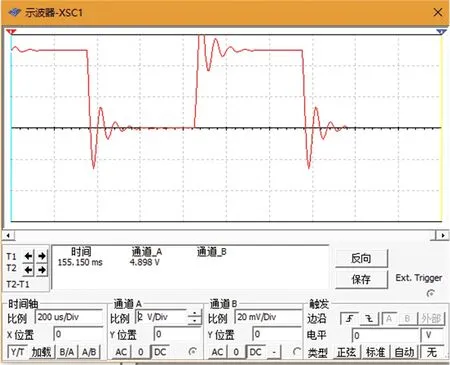
图7 欠阻尼状态暂态过程

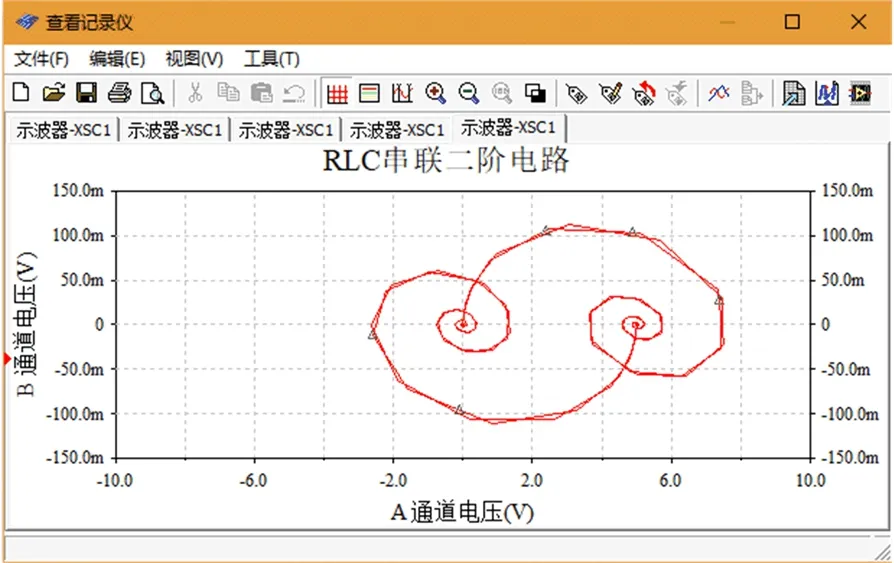
图8 欠阻尼状态轨迹

与传统的实验手段相比，Multisim仿真软件不需要专用的机房，不受时间和地点的限制，方便学生的学习。同时，软件的元件库中元件类型丰富，学生可以方便地选择所需要的元件，可以方便地构建自己设计的电路图，可以实时地观测电路的响应波形。这些都是传统的实验手段很难具备的。

3 结束语

通过前面的理论分析和软件仿真，可以使学生建立理论公式与实际的电压响应波形之间的联系，可以加深对RLC串联二阶电路的理性和感性认识。同时，通过对Multisim仿真软件的使用，也可以让学生自己动手，练习使用仿真软件进行电路的仿真实验，这样可以增加学生的学习兴趣，有利于学生养成勤于思考、主动学习的习惯。

[参 考 文 献]

[1] 李琳芳，刘艳昌，崔微微.基于Multisim与Matlab的二阶系统响应分析与仿真[J].河南科技学院学报,2015,43(4)：59-63.

[2] 李剑清.Multisim在电路实验教学中的应用[J].浙江工业大学学报，2007,35(5)：543-546.

[3] 齐迹.RLC串联二阶电路响应的分析与仿真[J].齐齐哈尔大学学报,2007,23(3)：33- 36.

[4] 李姿,李曼,王津.二阶电路暂态过程与状态轨迹的实验研究[J].科协论坛(下半月)，2013(08)：37-38.

[5] 李如琦，陈军灵.Multisim仿真软件在电工电子实验教学中的应用[J].广西大学学报，2005，27增刊，85-87.

[6] 邱关源. 电路·第5版[M]. 北京：高等教育出版社，2006.