沂河流域水文降雨预测模型研究
刘景青
(莒南县涝坡水利服务中心,山东 莒南 276600)
水文预报是水资源管理预报最主要的工作之一,目前,BP神经网络模型、小波神经网络(WANN)模型均已应用到了水文预测模型中,但由于BP神经网络模型收敛速度较慢、出错率较高,WANN模型在收敛速度与计算参数优化过程中同样存在一定的缺陷。极限学习机算法(ELM)是一种新型的单隐含层前馈神经网络算法,在训练中无需参数调整即可找出最优解,克服了传统神经网络算法收敛速度慢的缺点,目前已在农田蒸散预测、土壤渗透预测等方面得到了广泛应用。本文基于ELM算法建立水文预报过程预测模型,并与传统BP神经网络模型、WANN模型进行比较,验证ELM模型的精度。
1 计算方法
1.1 极限学习机算法模型
ELM模型主要可分为输入层、隐含层和输出层3部分。首先通过输入层输入所求变量,通过与隐含层之间的权重ωij,计算出输出层权重βjk和输出变量矩阵,得出最终结果。
极限学习算法将神经网络输出权重过程分为2步。在初始阶段,假定所求权重为β,假设初始输入权重为ai和输入偏置bi,输入层矩阵用H0表示,通过式(1)计算输出权重为β0:

式中:β0为输出权重,H0为输入层矩阵,T0为变量矩阵。
对于输出权重βi,可由下式计算:

根据求得的输出权重,与输出变量进行运算,最终求得极限学习机算法的最终模拟结果。本文中ELM模型算法采用Matlab2013a软件进行模拟计算。
1.2 计算误差比较
Nash-Sutcliffe系数(CD)、逐日相对均方根误差(RMSE)和 Kendall一致性系数(K)可以较好地反映长时间预测序列与实测值的误差和一致性,是系统性较好的数据评价指标体系。其中,CD与K的值越大、RMSE的值越小,模型算法与实测值的一致性越好、计算精度越高,具体公式如下:

式中:n为样本数量;P'为模型算法模拟值;Pm为实测值;为实测值的均值;A为待检验方法与实测结果中拥有一致性元素的对数;B为待检验方法与实测结果中不具有一致性元素的对数。
2 实例分析
沂河位于山东省临沂市,是山东省第一大河。全长300多公里,流域面积达到了11 820 km2,沂河集水面积4 800 km2,流域山丘区面积占总面积的70%,平原区占30%。沂河地处南北方气候过渡带,多年平均降雨量在800 mm左右,降雨主要集中在5~8月,降雨量较大,因此研究合理的模型预测该区域降水,对当地防洪政策的制定具有重要意义。
2.1 日降雨模拟精度对比
图1为3种不同计算模型模拟日降雨与实测降雨的对比。图1显示,ELM模型的计算精度明显高于BP神经网络模型和WANN计算模型,ELM模型模拟结果与实测值的拟合的决定系数R2达到了0.906 7,且相关性达到了极显著水平(P<0.01),同时拟合方程的斜率为1.297 1,而BP神经网络模型和WANN模型计算结果R2分别仅为0.452 8和0.48,且相关性均未达显著水平(P>0.05),拟合方程斜率分别为1.488 6和1.827,明显高于ELM模型的拟合方程斜率,因此,ELM模型计算结果与实测数据保持着较高的计算精度和一致性。
2.2 三种模型计算精度指标对比
表1为3种不同模型计算结果与实测值的计算精度指标分析。表1显示,ELM模型计算结果要明显优于BP神经网络模型与WANN模型,其逐日相对均方根误差RMSE仅为0.107,而BP神经网络模拟日降雨的计算结果RMSE值达到了0.647,WANN模型计算结果RMSE值达到了0.754;ELM模型对日降雨的模拟结果与实测值的一致性最高,其K值和CD值分别为0.934和0.917,决定系数R2也达到了0.907,且计算结果的相关性均达到了极显著水平(P<0.01),而BP神经网络模型与WANN模型的计算结果的一致性较差,K值分别为0.372和0.401,CD值分别为0.478和0.395,决定系数R2分别为0.453和0.480,且计算结果与实测值的相关性均未达显著水平(P>0.05)。综上所述,ELM模型因其RMSE值较低,K值、CD值与R2的值较高,表明该模型计算结果与实测值的计算误差最小,计算结果的一致性最高,因此,该模型可作为沂河流域水文降雨预报的计算标准模型。
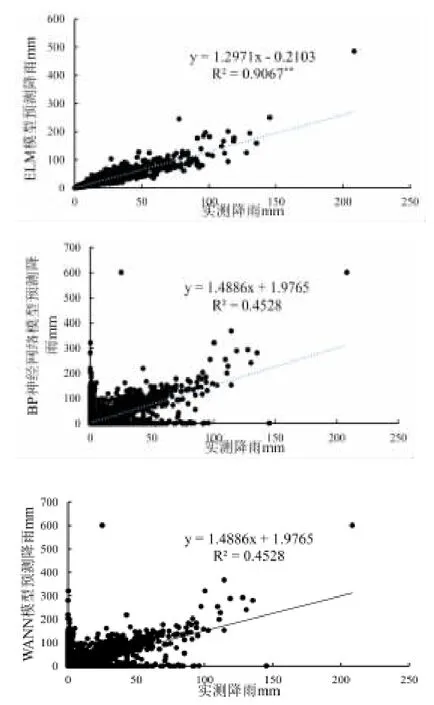
图1 三种模型模拟日降雨精度对比
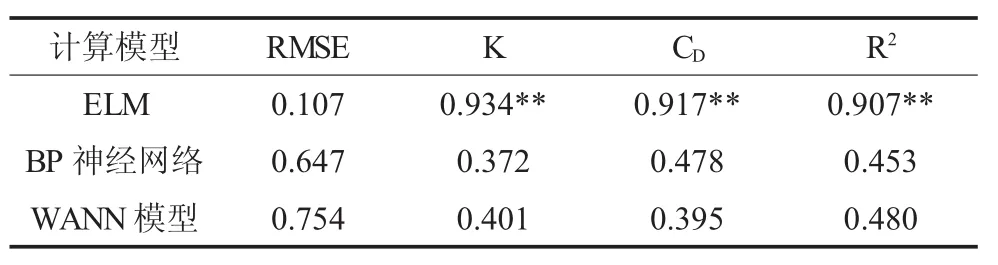
表1 三种模型模拟结果精度分析
[1] 邢柏锋.基于小波神经网络的径流预测方法分析 [J].科技创新与应用,2012,(11):41.
[2] 张建云.中国水文预报技术发展的回顾与思考 [J].水科学进展,2010,21(4):435—443.
[3] 古力皮亚·沙塔尔.改进的WANN模型在新疆中长期水文预报中的应用研究 [J].水利规划与设计,2016,(11):27—30+33.
[4] 冯禹,崔宁博,龚道枝,等.基于极限学习机的参考作物蒸散量预测模型 [J].农业工程学报,2015,31(增刊1):153-160.

