Nakagami-m衰落下中继系统性能分析
李兴旺, 李静静, 靳 进, 李立华
(1. 河南理工大学 物理与电子信息学院,河南 焦作 454000; 2. 北京邮电大学 网络与交换技术国家重点实验室,北京 100876; 3. 郑州大学 信息工程学院,河南 郑州 450001)
近年来,中继系统因其能够扩展覆盖范围、提高系统可靠性和服务质量而受到学术界和产业界的广泛关注[1-2]. 然而,现有文献主要集中在理想硬件条件下的中继系统. 在实际系统中,射频设备受到各类硬件损伤的影响,例如非线性功率放大器[3]、同相和正交相位(In-phase and Quadrature, I/Q)非平衡[4]以及相位噪声[5]. 上述损伤虽然可以通过适当的补偿和校准算法来减少硬件损伤对系统性能的影响,但是由于估计误差和校准不准确的原因,仍存在一些残留损伤,而这些残留损伤对系统性能仍产生重要的影响[6]. 此外,上述研究均是针对某单一损伤类型的,没有统一考虑各种损伤类型对系统性能的影响.
鉴于文献[3-5]研究中存在的不足,文献[7]中研究了硬件损伤对双跳中继系统性能的影响,推导出通用衰落信道下系统中断概率和容量性能的闭式表达式. 针对双向中继系统,文献[8]中分析了发送端存在硬件损伤条件下中继系统的性能,推导出双向中继系统中断概率和误符号率确切性能的闭式表达式. 利用有限维度和大维度随机矩阵理论,文献[9]中研究了收发端硬件损伤条件下双跳放大转发(Amplify-and-Forward, AF)中继系统的遍历容量性能,推导出系统遍历容量及上下界的闭式表达式.
上述文献为研究硬件损伤对中继系统性能的影响打下了坚实的基础.实际上,文献[7,9]中考虑了硬件损伤对双跳中继系统性能的影响,文献[8]研究了硬件损伤对双向中继系统的影响. 但是硬件损伤对存在直连情况的协作中继系统性能的影响上述文献没有涉及,从而也没有考虑接收端处理算法. 鉴于此,笔者研究了存在直连情况的双跳放大转发中继系统的中断概率性能. 在此考虑Nakagami-m衰落信道模型,原因在于Nakagami-m是一个通用模型,能够有效地表征多种衰落信道.例如,α=1/2,表示单边带高斯信道;α=1,表示瑞利衰落信道;α=∞,表示无衰落的加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道等. 另外,笔者考虑两种通信场景:源节点和目的节点不仅通过中继系统进行连接,而且两者之间存在直连路径;源节点和目的节点通过双跳固定增益放大转发中继系统连接,不存在直连路径. 在第1种场景中,接收端使用选择合并(Selection Combining, SC)算法. 推导出两种场景下系统中断概率性能的确切闭式表达式,所得闭式表达式适用于任意衰落参数以及损伤参数,同时在整个信噪比(Signal-to-Noise Ratio, SNR)范围内所得理论分析结果能够充分逼近蒙特卡罗仿真结果.
1 系统模型
考虑存在直连情况下的中继模型,包括一个源节点、一个中继节点和一个目的节点,所有节点配置单天线. 定义源节点与中继节点、中继节点与目的节点以及源节点与目的节点之间的传输参数下标分别为1,2和3, 则中继节点和目的节点接收信息可以表示为
yi=hi(si+ηt,i)+ηr,i+vi,i∈{1, 2, 3} ,(1)
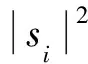

其中,κt,i和κr,i分别表示发送端和接收端硬件损伤参数,κt,i≥0,κr,i≥0.

(3)
其中,αi和βi分别为伽马函数的形状和尺度参数,βi=E{ρi}αi; Γ(αi)为伽马函数[11]. 利用文献[11],可得伽马分布的累计分布函数为
(4)
结合式(2),式(1)可以重新表述为以下简单形式[7]:
yi=hi(si+ηi)+vi,(5)

对于上述系统模型,考虑源节点与目的节点通过两种场景进行通信:源节点和目的节点不仅通过放大转发中继系统连接,而且两者之间存在直连情况;源节点和目的节点仅通过放大转发中继系统连接,不考虑两者直连情况. 以下分别给出两种场景的具体传输过程.
1.1 第1种场景
在此场景下,整个通信过程分为两个时隙.
第1时隙: 源节点同时向中继节点和目的节点发送信息. 结合式(5),中继节点和目的节点接收到的信息可分别表示为
第2时隙: 中继节点接收到源节点发送的信息,进行放大后转发到目的节点,则目的节点接收的信息为
y2=h2G(h1(s1+η1)+v1)+η2+v2=Gh1h2s1+Gh1h2η1+Gh2v1+h2η2+v2,(8)
其中,G为硬件损伤下的放大系数[7],其定义为
(9)
当κ1=0时,式(9)退化为理想硬件下的放大系数.
因此,目的节点处的接收信噪比可分别表述为
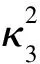
在接收端通过选择合并算法处理目的节点接收的信息.选择合并算法即输出信噪比最高的那个支路上的信号. 所以,采用选择合并算法输出的信噪比等于各支路信噪比的最大值,即接收端信噪比可表示为
γsc=max(γ2,γ3) ,(12)
其中,γ2和γ3分别由式(11)和式(10)决定.
1.2 第2种场景
在以上场景的基础上,第2种场景仅考虑源节点和目的节点间通过放大转发中继系统连接,不考虑源节点与目的节点直连的情况. 第1时隙传输过程与上述场景不同.
第1时隙: 源节点仅向中继节点发送信息.
第2时隙: 中继节点将接收到的信息进行放大后转发到目的节点,则目的节点接收到的信息为
y2=Gh1h2s1+Gh1h2η1+Gh2v1+h2η2+v2.(13)
因此,目的节点处的接收信噪比可表述为
(14)
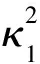
2 中断概率
中断概率是用于评价通信系统服务质量的重要性能指标,其定义为端到端的瞬时信噪比低于某一固定阈值γth的概率[12],即
Pout(γth)=P(γ≤γth) .(15)
2.1 第1种场景
在第2个时隙,目的节点选择合并来自中继节点和源节点的信息. 因此,当中继节点和源节点发送信息的信噪比均小于阈值时,将发生中断.
定理1 在Nakagami-m衰落信道下,存在直连情况的硬件损伤双跳放大转发中继系统中断概率可表示为
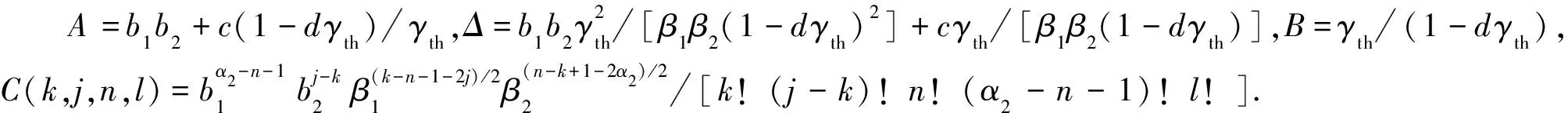
证明 结合式(3)、式(4)和式(11),源节点与目的节点通过中继通信链路的中断概率可表示为
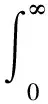
当γth≥1d时,式(17)等于0; 当γth<1d时,式(17)可以化简为
(18)
为了便于计算,利用变量代换z=ρ2-b1γth(1-dγth),则式(18)可进一步化简为
利用二项式展开定理,可得
将I1和I2代入式(19), 然后利用文献[11]的积分等式:
(20)
式(19)可进一步表示成闭合形式:
(21)
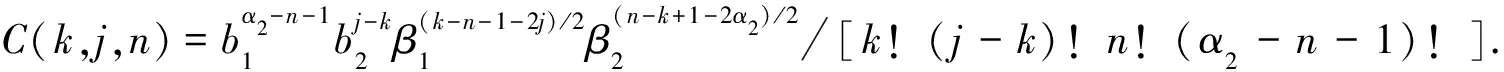
结合式(4)和式(10),直连路径处的中断概率表达式可表示为
存在直连情况的中继系统对应的中断概率为
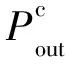
将式(21)和式(22)代入式(23),即可得到第1种场景下系统中断概率的表达式. 证毕.
2.2 第2种场景
定理2 在Nakagami-m衰落信道下,硬件损伤双跳放大转发中继系统的中断概率可表示为
(24)
证明 第2种场景是在第1种场景的基础上考虑源节点与目的节点不存在直连路径的情形. 因此,定理2的证明可参考定理1的证明过程.
3 仿真结果
图1仿真了两种场景下系统中断概率随信噪比变化的曲线.两种场景参数设置如下: 损伤参数κ= 0.1(理想硬件参数是κ=0),衰落参数α=2,阈值γth= 22-1= 3和γth= 25-1= 31[7]. 由图1可知两种场景下,式(16)和式(24)的理论分析表达式的结果能够与蒙特卡罗仿真结果充分拟合,从而验证了笔者理论分析的正确性. 此外,图1还表明: 当取较低的阈值 (γth=3) 时,收发端硬件损伤对系统中断概率性能的影响较小. 随着阈值增大 (γth=31),非理想硬件(实线)与理想硬件(虚线)之间的间隙随之增大,这表明随着中断阈值的增大,收发端硬件损伤对系统性能的影响越来越显著,并且系统的中断性能也随着阈值的增大而下降. 图1表明,由于直连路径的存在,第1种场景的性能要优于第2种场景的.
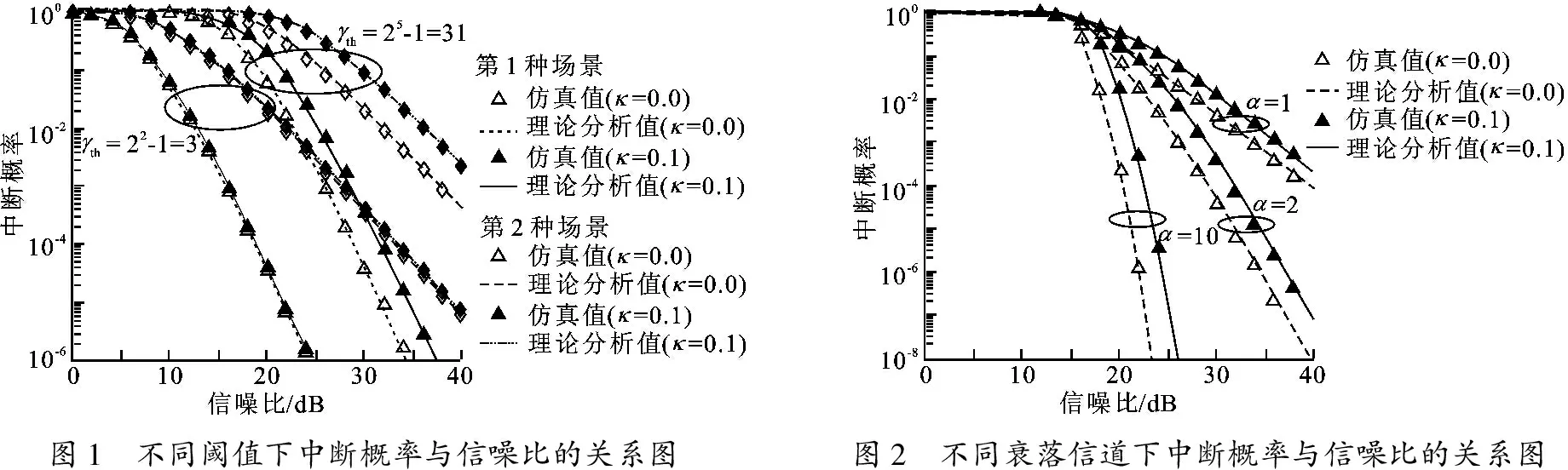
图1 不同阈值下中断概率与信噪比的关系图图2 不同衰落信道下中断概率与信噪比的关系图
图2仿真了第1种场景下基于不同衰落参数值下存在直连情况的中继系统的中断概率随信噪比的变化曲线.具体参数设置如下: 损伤参数κ= 0.1(理想硬件参数κ=0),阈值γth=31,衰落参数α= {1, 2, 10}. 由图2可知,在各种衰落参数下,理论分析值和蒙特卡罗仿真值充分一致. 此外,图2表明,存在直连情况的中继系统的中断概率性能随着衰落参数α的值增加而增加. 图2还表明,非理想硬件(实线)与理想硬件(虚线)之间的间隙随着α的增大而增大,这表明收发端硬件损伤对系统中断性能的影响随着衰落参数的增大而越发显著. 最后,由图2可以看出,非理想和理想硬件性能之间的差别随着信噪比增加而逐渐增大.
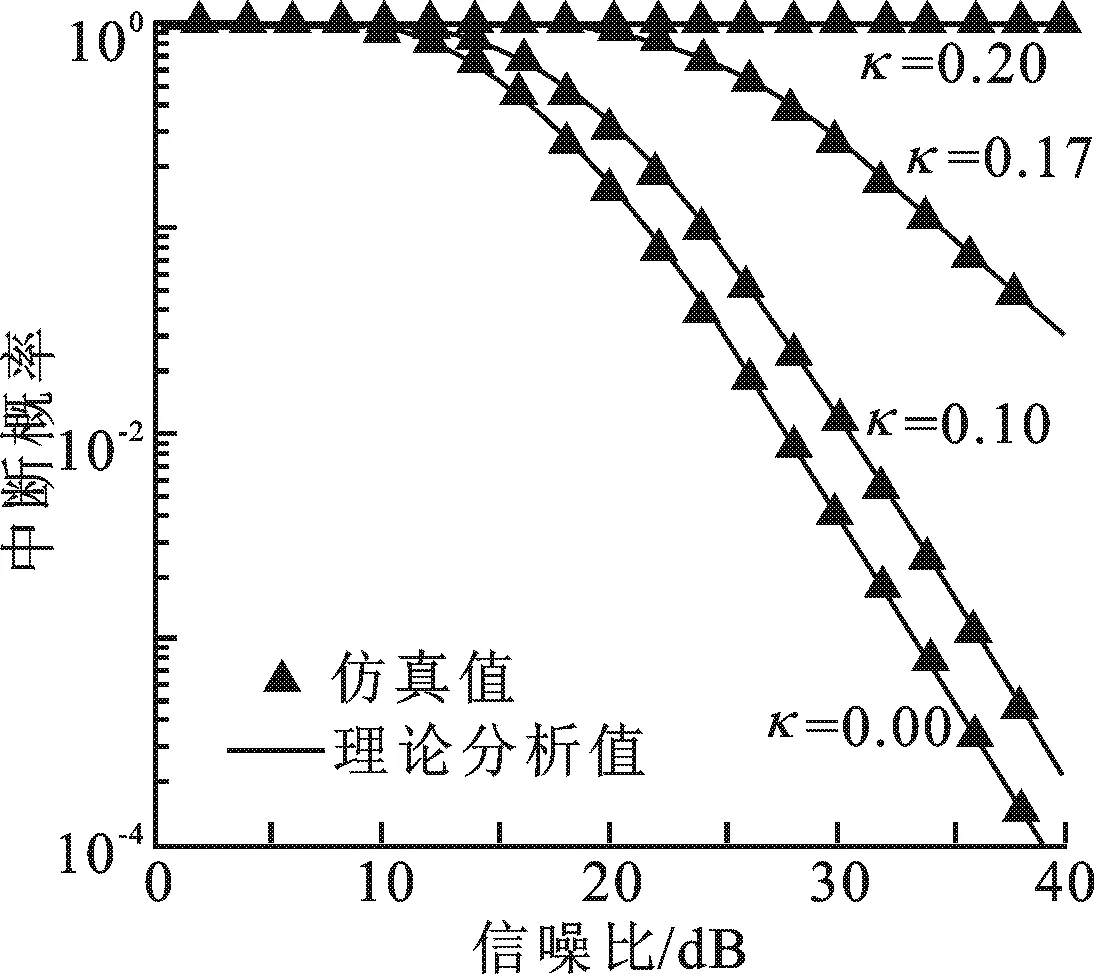
图3 不同损伤程度下中断概率与信噪比的关系图
图3仿真了第1种场景不同硬件损伤下存在直连情况的中继系统的中断概率随信噪比的变化曲线.具体参数设置如下: 损伤参数κ= {0, 0.10, 0.17, 0.20},衰落参数α=1,阈值γth=31. 由图3可知,当损伤参数κ=0.2 时,中断概率几乎为1,即系统一直处于中断状态. 随着损伤参数的减小,存在直连情况的中继系统的中断概率性能逐渐增强. 当损伤参数κ=0 时,系统退化成理想硬件系统. 图3还表明,硬件损伤在低信噪比时的影响较小,但是在高信噪比时对系统中断性能有较大的影响.
4 结 束 语
笔者研究了基于Nakagami-m衰落信道两种场景下硬件损伤中继系统的性能,推导出了两种场景下系统中断概率的闭式表达式. 研究表明,存在直连情况的中继系统的中断概率受中断阈值、硬件损伤以及衰落信道的影响;系统性能随着中断阈值与损伤参数值的增加而减少,随着衰落参数值的增加而增加. 在任意参数设置下,理论分析结论与蒙特卡罗仿真结论一致,验证了理论分析的正确性.
[1] LANEMAN J N, TSE D N C, WORNELL G W. Cooperative Diversity in Wireless Networks: Efficient Protocols and Outage Behavior[J]. IEEE Transactions on Information Theory, 2004, 50(12): 3062-3080.
[2] 孙彦景, 刘雯, 曹起, 等. 联合功率分配的全双工MIMO中继最小速率优化[J]. 西安电子科技大学学报, 2018, 45(2): 115-120.
SUN Yanjing, LIU Wen, CAO Qi, et al. Minimum Rate Optimization on the Joint Power Allocation Full-duplex MIMO Relay[J]. Journal of Xidian University, 2018, 45(2): 115-120.
[3] KUMAR N, BHATIA V. Outage Analysis of OFDM Based AF Cooperative Systems in Selection Combining Receiver over Nakagami-mFading Channels with Nonlinear Power Amplifier[C]//Proceedings of the 2015 Sensor Signal Processing for Defence. Piscataway: IEEE, 2015: 7288516.
[4] LI J, MATTHAIOU M, SVENSSON T. I/Q Imbalance in AF Dual-hop Relaying: Performance Analysis in Nakagami-mFading [J]. IEEE Transactions on Communications, 2014, 62(3): 836-847.
[5] PITAROKOILIS A, MOHAMMED S K, LARSSON E G. Uplink Performance of Time-reversal MRC in Massive MIMO Systems Subject to Phase Noise[J]. IEEE Transactions on Wireless Communications, 2015, 14(2): 711-723.
[6] STUDER C, WENK M, BURG A. MIMO Transmission with Residual Transmit-RF Impairments[C]//Proceedings of the 2010 International ITG Workshop on Smart Antennas. Piscataway: IEEE, 2010: 189-196.
[7] BJORNSON E, MATTHAIOU M, DEBBAH M. A New Look at Dual-hop Relaying: Performance Limits with Hardware Impairments[J]. IEEE Transactions on Communications, 2013, 61(11): 4512-4525.
[8] MATTHAIOU M, PAPADOGIANNIS A, BJORNSON E, et al. Two-way Relaying under the Presence of Relay Transceiver Hardware Impairments[J]. IEEE Communications Letters, 2013, 17(6): 1136-1139.
[9] PAPAZAFEIROPOULOS A K, SHARMA S K, CHATZINOTAS S, et al. Ergodic Capacity Analysis of AF DH MIMO Relay Systems with Residual Transceiver Hardware Impairments: Conventional and Large System Limits[J]. IEEE Transactions on Vehicular Technology, 2017, 66(8): 7010-7025.
[10] 郭漪, 吕昱萱, 刘刚, 等. D2D通信中最优功率分配和最佳中继选择[J]. 西安电子科技大学学报, 2017, 44(4): 7-13.
GUO Yi, LÜ Yuxuan, LIU Gang, et al. Optimal Power Allocation and Best Relay Selection in D2D Communication[J]. Journal of Xidian University, 2017, 44(4): 7-13.
[11] GRADSHTEYN I S, RYZHIK I M. Table of Integrals, Series, and Products[M]. 7th Edition. Boston: Academic Press, 2007.
[12] LI X, YANG X, LI L, et al. Performance Analysis of Distributed MIMO with ZF Receivers over Semi-correlated K Fading Channels[J]. IEEE Access, 2017, PP(99): 1.

