分布式结构下主/被动雷达抗假目标干扰方法
刘洁怡, 张林让, 赵珊珊, 刘 楠, 于恒力
(1. 西安电子科技大学 雷达信号处理国家重点实验室,陕西 西安 710071;2. 南京邮电大学 电子与光学工程学院,江苏 南京 210023)
随着现代电子战争日趋激烈,有源欺骗式干扰因具有低成本、高性价比的特点而被广泛应用,对雷达系统的工作性能和生存能力构成了严峻的挑战和威胁[1-5].作为电子干扰的发生器,数字射频存储器(Digital Radio Frequency Memory,DRFM)等器件的成熟应用为对抗欺骗式假目标干扰的工作带来了技术难度.数字射频存储器可通过截获、存储、转发雷达信号,实现在真实目标附近产生与时域、频域和空域特征都十分相似的假目标以干扰组网雷达系统.在信号处理阶段,抗干扰措施往往无法完全对抗该高逼真度假目标,导致假目标最终形成点迹;进入雷达数据处理阶段,甚至形成稳定的航迹.此时,假目标将影响雷达对真实目标的跟踪精度,同时严重消耗雷达系统资源.
针对组网雷达抗欺骗式假目标干扰,文献[6]提出了用于集中式组网雷达的自适应门限同源检验的假目标鉴别方法,文献[7]提出了用于分布式组网雷达的航迹同源检验的方法,这两种方法均是利用主动雷达进行假目标鉴别的.对于由异地配置的主/被动雷达构成的异构雷达网,文献[8]提出了基于方位角统计量的主/被动雷达抗多假目标干扰的方法,但由于其仅利用了被动雷达的方位角信息,对假目标的误鉴别概率较高; 文献[9]采用三维分配算法的主/被动雷达和基于基准线最小距离法对各个目标进行联合处理.相比于文献[8]中的方法,联合处理可以提高正确鉴别概率并且降低误鉴别概率. 文献[8-9]中的主/被动雷达网抗假目标方法均仅适用于集中式融合结构.由于分布式组网雷达中,航迹生成后剔除了没有生成航迹的冗余点,从而单位时刻对比,分布式融合结构比集中式融合结构中检测到的点迹数据少,被欺骗的可能性降低[10-11].如何在该融合结构下更好地完成对假目标的鉴别,目前尚未见到公开发表的文献.
针对异地配置的主/被动雷达系统,笔者提出一种基于分布式融合结构的距离欺骗式假目标鉴别算法.该算法对假目标进行两次鉴别:在利用主动雷达联合被动雷达起始航迹阶段,对主/被动雷达中的点迹进行关联检验,可去除距离真实目标较远的部分假目标,所使用的点迹关联算法是基于角度统计量的方法,在文献[8]中方位角统计量的基础上进一步利用了被动雷达的俯仰角信息,降低了误关联概率; 在数据处理阶段,对已形成稳定航迹的假目标,进一步利用航迹关联算法对其进行鉴别.
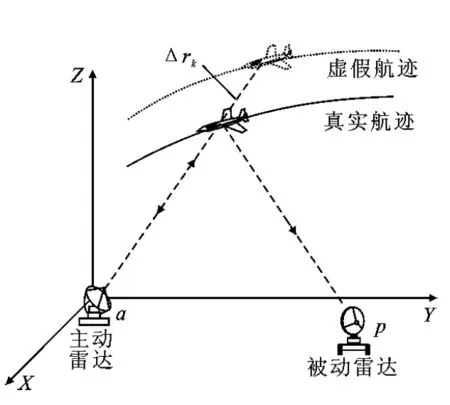
图1 异地配置的主/被动雷达布站及真假目标航迹示意图
1 信号模型
异地配置的主/被动雷达布站及真假目标航迹信息如图1所示.不失一般性,考虑该异构雷达网系统由1部主动雷达和1部被动雷达组成.为了掩护真实目标,携带式干扰机会对雷达进行欺骗式干扰,在真实目标附近产生虚假目标. 笔者仅考虑距离欺骗假目标干扰,通过干扰机产生与真实回波具有不同时延的假目标回波,即可表示为在真实目标与雷达连线的延长线上产生虚假目标,从而达到对各节点雷达实施距离欺骗式干扰的目的[12].
1.1 多假目标欺骗干扰模型

1.2 主/被动雷达量测模型
主动雷达可得到目标的径向距离、方位角和俯仰角信息,对目标的观测方程为
(1)
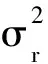
被动雷达可得到目标的方位角和俯仰角信息,对目标的观测方程为
(2)
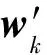
2 主/被动雷达航迹初始化
针对主/被动雷达系统,提出了一种基于分布式融合结构的抗欺骗式假目标干扰的方法.该方法包括主/被动雷达跟踪滤波、航迹关联、航迹融合3个部分,并在航迹起始和航迹关联两个阶段对假目标进行鉴别.该主/被动雷达系统的数据处理流程如图2所示.
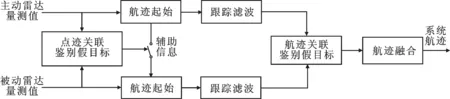
图2 主/被动雷达系统数据融合处理流程图
被动雷达的观测信息只有目标的方位角和俯仰角,无法得到目标的空间位置坐标,不能独立地对新生目标起始航迹.笔者利用主动雷达的观测信息,并将其转换到被动雷达的跟踪滤波的坐标系中,联合被动雷达对新生目标进行初始化.首先对主/被动雷达在航迹起始阶段的观测信息进行点迹关联,若关联成功,则利用主动雷达的观测信息联合被动雷达进行航迹起始,并判定主动雷达和被动雷达中没有关联上任何点迹的量测值对应于假目标,予以剔除.文献[9]中基于角度统计量进行点迹关联的方法仅利用了被动雷达的方位角信息,导致其误关联的概率较高,笔者在此基础上进一步融合了被动雷达的俯仰角信息,在一定程度上降低了误关联概率.
设主动雷达在t=k时刻的观测值Zk=[rk,θk,φk]T,则目标在直角坐标系下的坐标为
(3)
由主动雷达的观测值,估计得到的目标相对于被动雷达的观测值为
(4)
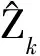
(5)
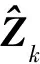
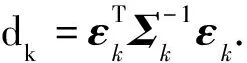
(6)
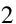
值得注意的是,在被动雷达的航迹起始阶段存在这样一个矛盾:当被动雷达中的一个点迹和主动雷达的多个点迹关联时,若不进行多义性处理,则会使得被动雷达中的目标被重复起始; 若进行多义性处理,则会增大真实目标被误判为假目标的概率,导致真实目标丢失.针对此矛盾,笔者对点迹关联的结果进行如下处理: 利用多义性处理后的结果起始被动雷达航迹,即利用关联距离最小的主动雷达的量测值对被动雷达进行航迹起始; 利用多义性处理前的结果对主/被动雷达中的目标进行真假目标鉴定,判定主动雷达和被动雷达中没有关联上任何点迹的量测值对应于假目标,予以剔除.
当关联结果存在多义性时,上述的处理方式可能会导致利用假目标的观测值对被动雷达中的目标进行航迹起始的情况,但由于此时假目标的位置与真实目标的位置较近,误差稍大的起始点并不会对被动雷达的航迹起始产生过大的影响,被动雷达仍可以成功对目标进行初始化.这种方式在尽可能地保证真实目标不被剔除的前提下,可去除距离真实目标较远的部分假目标,而对于通过点迹关联检验的假目标仍会形成稳定航迹,将进一步利用航迹关联的方法对其进行鉴别与剔除.
3 航迹关联鉴别假目标方法
通过对主动雷达和被动雷达的目标航迹进行航迹关联,可进一步鉴别出主动雷达中的假目标航迹.在进行航迹关联之前,假设两个雷达跟踪滤波得到的航迹已进行空间对准和时间对齐[14].
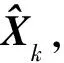
(7)

设假设H0表示两条航迹对应于同一目标,H1为其对立假设:
(9)
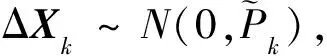
(10)
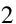
对两部雷达的航迹进行两两关联后,根据检验统计量Ω对最终关联结果进行多义性处理,保证主动雷达中的每一条航迹最多仅能和被动雷达中的一条航迹进行关联.最终,若主动雷达中存在航迹没有关联上被动雷达中的任何航迹,则判定该航迹对应于假目标,将其剔除.
4 仿真实验
根据第1节给出的主/被动雷达及数据模型进行仿真.参考现有地基雷达系统[6-9],设置主动雷达的位置坐标为(0,0,0),其测距误差为 25 m,方位角误差和俯仰角误差均为0.3°,测速误差为 7 m/s; 被动雷达的位置坐标为 (10 000 m,0 m,100 m),由于被动雷达的测角误差大于主动雷达,设置方位角误差和俯仰角误差均为1°.假设空间中仅有1个真实目标,根据独立性条件[2-3],初始位置坐标设置为 (3 500 m,40 000 m,20 000 m),初始速度矢量为 (-10 m/s,-400 m/s,-20 m/s),目标在观测期间始终做匀速直线运动,目标运动标准差为0.05.假目标的个数为2,欺骗距离在观测期间不变,分别为 Δrk= ±2 000 m,两部雷达的数据间隔均为 1 s,观测时间总长度为 200 s.
4.1 主/被动雷达航迹起始仿真
利用笔者提出的方法对主动雷达和被动雷达观测到的量测值进行航迹起始,在不同起始时间段长度K下,统计出被动雷达目标被成功起始航迹的概率P,利用多义性处理前的关联结果进行真假目标鉴别得到的对真实目标的误鉴别概率Pt和对假目标的误鉴别概率Pf,利用多义性处理后的关联结果进行真假目标鉴别得到的对真实目标的误鉴别概率Pt和对假目标的误鉴别概率Pf,如表1所示.假设检验的显著性水平α= 0.01,蒙特卡罗仿真次数为 5 000 次.
表1主/被动雷达的航迹起始概率表%
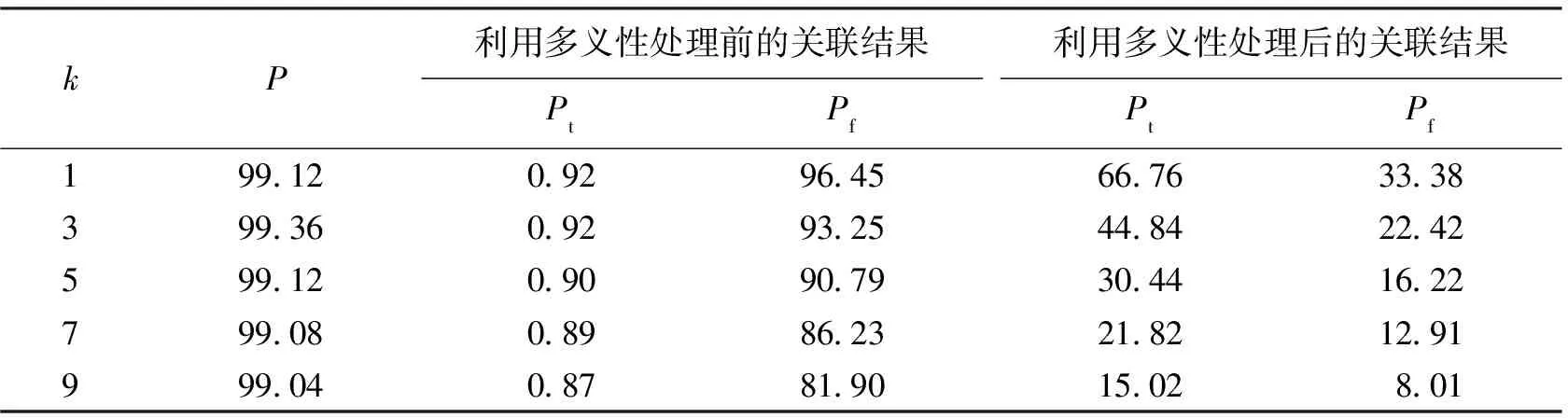
kP利用多义性处理前的关联结果PtPf利用多义性处理后的关联结果PtPf199.120.9296.4566.7633.38399.360.9293.2544.8422.42599.120.9090.7930.4416.22799.080.8986.2321.8212.91999.040.8781.9015.028.01
从表1中,可以看到:
(1) 被动雷达目标被成功起始的概率P均保证在99%以上.
(2) 利用多义性处理前的结果进行真假目标鉴别,可保证对真实目标的误鉴别概率Pt均在1%以下,但对假目标的误鉴别概率Pf过高.随着航迹起始时间段长度不断增大,对假目标的误鉴别概率Pf不断降低.
(3) 对点迹关联的结果进行多义性处理,可降低对假目标的误鉴别概率Pf,但同时大幅提高了对真实目标的误鉴别概率Pt,这将导致主动雷达中真实目标被剔除的概率变大.尽管通过增大航迹起始时间段长度,可进一步降低对真实目标的误鉴别概率Pt,但是航迹起始时间长段一般不宜过长,在k=9 的情况下,对真实目标的误鉴别概率Pt为15.02%,此时真实目标仍有15.02%的概率会被剔除,说明利用多义性处理后的关联结果进行真假目标鉴别是不可取的.
为了尽量保证主动雷达中的真实目标不会被剔除掉,在航迹起始阶段选择利用多义性处理前的关联结果进行真假目标鉴别.此时,保证了对真实目标的误鉴别概率Pt最小,但付出的代价是对假目标的误鉴别概率很高,说明需要进一步利用航迹关联对假目标进行鉴别与剔除.
4.2 航迹关联鉴别假目标仿真
在进行航迹起始后,主动雷达和被动雷达均利用匀速运动模型对目标进行跟踪滤波.为验证航迹关联鉴别假目标的能力,设航迹起始阶段并没有剔除掉假目标,假目标均已形成稳定航迹.因此,主动雷达跟踪出3条稳定航迹,分别对应于真实目标和两个假目标,被动雷达跟踪到1条稳定航迹,对应于真实目标.
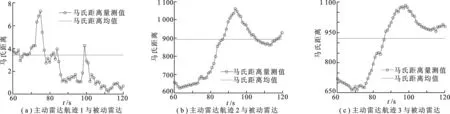
图3 主/被动雷达两两航迹间在各个时间点的马氏距离
根据第3节中所述的序贯航迹关联检验方法,对主动雷达和被动雷达中的目标航迹进行关联检验,如图3所示,得到主动雷达中各条航迹与被动雷达航迹之间在各个时间点的马氏距离.
选择航迹关联检验的时间段为1~200 s,对各个时间点的马氏距离进行求和,得到航迹关联的鉴别统计量.主动雷达中各条航迹与被动雷达航迹之间的鉴别统计量如表2所示.

表2 主/被动雷达两两航迹间的鉴别统计量
对航迹关联检验算法进行10万次蒙特卡罗仿真实验,统计结果显示,真实目标关联成功的概率为96.04%,对假目标航迹的误鉴别概率为零,均优于文献[8]中图5、图6的仿真结果.统计结果验证了笔者提出算法的稳定性,在保证较高的真实目标鉴别概率的前提下,可成功剔除假目标航迹.相比于文献[8]中基于集中式融合结构的方法,笔者提出的方法有效地降低了对假目标的误鉴别概率,该优势主要是由分布式融合结构中的时间融合和空间融合的结合带来的.
5 结 束 语
笔者论述了一种基于分布式融合结构的主/被动雷达抗欺骗式假目标干扰的方法.首先对主动雷达和被动雷达中的点迹信息进行关联检验,在关联成功的情况下,利用主动雷达中的量测值联合被动雷达进行航迹起始,并利用关联结果对真假目标进行鉴别,以剔除部分假目标.对主动雷达中已形成稳定航迹的假目标,进一步利用航迹关联检验的方法进行剔除.这种分布式处理方式能以较低的费用获得较高的可靠性和可用性,同时有效地降低对假目标的误判概率.仿真结果表明,笔者提出的方法可以保证在较高的真实目标鉴别概率的前提下,对欺骗式假目标进行有效的鉴别,降低主/被动雷达的被欺骗概率.
[1] ZHANG J D, ZHU D Y, ZHANG G. Antivelocity Deception Jamming Technique Using Pulses with Adaptive Initial Phases[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1290-1300.
[2] LIU J Y, ZHANG L R, ZHAO S S, et al. Echo Correlation Analysis in Diversity Multiple-input Multiple-output Radars[J]. IET Radar, Sonar and Nsacigation, 2016, 10(6): 1112-1117.
[3] LIU J Y, ZHANG L R, ZHAO S S, et al. Correlation Characteristic Analysis in Diversity Multiple-input Multiple-output Radar[J]. Electronics Letters, 2017, 53(5): 349-351.
[4] 吴亿锋, 王彤, 吴建新. 转发式干扰环境中的机载雷达运动目标检测[J]. 西安电子科技大学学报, 2014, 41(6): 51-56.
WU Yifeng, WANG Tong, WU Jianxin. Moving Target Detection for Airborne Radar under Repeater Jamming Environment[J]. Journal of Xidian University, 2014, 41(6): 51-56.
[5] ZHANG J D, ZHU D Y, ZHANG G. New Antivelocity Deception Jamming Technique Using Pulses with Adaptive Initial Phases [J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1290-1300.
[6] 赵艳丽, 王雪松, 王国玉, 等. 多假目标欺骗干扰下组网雷达跟踪技术[J]. 电子学报, 2007, 35(3): 454-458.
ZHAO Yanli, WANG Xuesong, WANG Guoyu, et al . Tracking Techniquefor Radar Network in the Presence of Multi-range-false- target Deception Jamming[J]. Acta Electronica Sinica, 2007, 35(3): 454-458.
[7] 赵艳丽, 陈永光, 蒙洁, 等. 分布式组网雷达抗多假目标欺骗干扰处理方法[J]. 电光与控制, 2011, 18(3): 25-30.
ZHAO Yanli, CHEN Yongguang, MENG Jie, et al. A Data Processing Method Against Multi-false-target Deception Jamming for Distributed Radar Network [J]. Electronics Optics & Control, 2011, 18(3): 25-30.
[8] 李世忠, 王国宏, 徐海全, 等. 异地配置的主/被动雷达抗多假目标干扰[J]. 火力与指挥控制, 2013, 38(5): 10-13.
LI Shizhong, WANG Guohong, XU Haiquan, et al. Study on Algorithm Against Multi-false-target Deception Jamming for Active/Passive Radar at Different Sites [J]. Fire Control & Command Control, 2013, 38(5): 10-13.
[9] 李世忠, 王国宏, 徐海全, 等. 三维空间主/被动雷达抗多假目标干扰研究[J]. 现代防御技术, 2012, 40(6): 118-124.
LI Shizhong, WANG Guohong, XU Haiquan, et al. Algorithm Against Multi-false-target Deception Jamming for Three- dimensional Active/Passive Radar at Different Sites [J]. Modern Defence Technology, 2012, 40(6): 118-124.
[10] 熊伟, 张晶炜, 何友. 基于多维分配和灰色理论的航迹关联算法[J]. 电子与信息学报, 2010 , 32(4): 898-901.
XIONG Wei, ZHANG Jingwei, HE You. Track Correlation Algorithm Based on Multi-dimension Assignment and Gray Theory[J]. Journal of Electronics & Information Technology, 2010, 32(4): 898-901.
[11] ZHAO S S, ZHANG L R, ZHOU Y, et al. Signal Fusion-based Algorithms to Discriminate between Radar Targets and Deception Jamming in Distributed Multiple-radar Architectures[J]. IEEE Sensors Journal, 2015, 15(11): 6697-6706.
[12] ZHAO S S, LIU N, ZHANG L R, et al. Discrimination of Deception Targets in Multistatic Radar Based on Clustering Analysis[J]. IEEE Sensors Journal, 2016, 16(8): 2500-2508.
[13] SCHUERGER J, GARMATYUK D. Deception Jamming Modeling in Radar Sensor Networks[C]//Proceedings of the 2008 IEEE Military Communications Conference. Piscataway: IEEE, 2008: 4753118.
[14] SOYSAL G, EFE M. Data Fusion in a Multistatic Radar Network Using Covariance Intersection and Particle Filtering[C]//Proceedings of the 2011 14th International Confercence on Information Fusion. Piscataway: IEEE, 2011: 5977555.

