外辐射源雷达参考通道多径干扰抑制方法

郭 帅， 王 俊， 陈 刚， 王 珏

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

近年来，外辐射源雷达依靠其双基体制和沉默接收的独特优势成为国内外研究的热点．传统的外辐射雷达主要利用民用和商用信号作为机会照射源信号进行目标探测和成像[1]，比如调频(Frequency Modulation， FM)广播信号[2-6]、全球移动通信系统(Global System for Mobile communication， GSM)信号、全球定位系统(Global Position System， GPS)信号、数字广播(Digital Audio Broadcast， DAB)信号和数字电视地面广播(Digital Video Broadcast-Terrestrial， DVB-T)信号[7]．为充分发掘外辐射源雷达的巨大潜力，可供利用的照射源信号的范围可以进一步扩大，利用非合作脉冲雷达作为照射源来进行目标探测．相对于民用连续波信号，雷达脉冲信号具有更大的功率，利用有源雷达的脉冲信号为辐射源信号可以获得更大的探测威力．各研究机构对基于脉冲信号的外辐射雷达系统进行研究，并发表了相关论文[8-9]．

由于山地和近地建筑的反射作用，外辐射源雷达不可避免地受到多径干扰的影响．当参考通道受到多径干扰影响时，参考通道接收的参考信号中包括直达波信号、多径干扰和通道噪声．如果含有多径干扰的参考信号直接用于匹配滤波处理，距离-多普勒图上会呈现多径干扰与目标回波信号相匹配形成的虚假目标．与监视通道中多径干扰造成的虚假目标不同，参考通道中多径干扰形成的虚假目标与对应真实目标的多普勒频移相同，虚假目标与真实目标的距离与多径干扰的时延有关，这些虚假目标可以看成真实目标的衍生目标．

目前，盲信号处理方法应用于外辐源雷达信号[10]．针对参考通道中的多径干扰问题，研究主要集中在利用盲均衡算法抑制参考通道中的多径干扰．由于直达波信号来自非合作的照射源，信号先验信息和多径信道都是未知的，在缺少训练序列的情况下，盲均衡算法是一种较为有效的多径干扰抑制算法．根据机会照射源信号恒模的特点，将恒模算法(Constant Modulus Algorithm， CMA)应用到参考通道盲均衡中，抑制参考通道中的多径干扰[11-13]．文献[11]提出分数阶恒模算法，并将其应用到多径信道盲均衡中．文献[12]提出一种恒模算法与多模算法相结合的改进算法，应用于非合作式双基脉冲雷达系统中，对直达波信号进行重构．文献[13]将多维恒模算法应用于基于调频信号的外辐射源雷达系统中，提出空时恒模算法(Space-Time-CMA， ST-CMA)，消除参考通道中的多径干扰．但是，空时恒模算法需要一组阵列天线来接收参考信号，增加了系统的复杂度和成本．

笔者首先推导脉冲压缩过程，证明参考通道中的多径干扰会造成虚假目标的出现；然后提出改进恒模算法来抑制参考通道中的多径干扰．与传统的恒模算法相比，笔者提出的算法具有更好的收敛性，更好地抑制多径干扰，有效地消除多径干扰造成的虚假目标，提高雷达系统的探测性能．

1 信号模型和脉冲压缩

1.1 信号模型

在外辐射雷达系统中，参考通道利用指向非合作照射源的参考天线接收直达波信号．假设非合作照射源的发射信号是线性调频(Linear Frequency Modulation， LFM)脉冲信号，参考通道接收到的多径干扰可以看成延迟的直达波信号，表示为

(1)

其中，sd(t)为直达波信号，h(t)为多径信道响应，an为响应幅度，τn为第n个多径干扰信号相对与直达波信号的时延，δ(t-τn)是时延为τn的脉冲响应．

参考通道接收的参考信号包含直达波信号、多径干扰信号和参考通道噪声，可以表示为

(2)

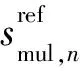
监视通道接收到的信号包含直达波信号、多径干扰、目标回波信号和监视通道噪声．利用扩展相消算法(Extensive Cancellation Algorithm， ECA)消除监视通道中的直达波信号和多径干扰，扩展相消算法投影矩阵表示为

(3)

其中，ssur表示监视通道接收的回波信号．

因为参考信号中的直达波信号和多径干扰信号都具有较大的信噪比，所以干扰相消时忽略参考通道噪声的影响，得到投影矩阵:

(4)

从投影矩阵W看出，当参考信号中含有多径干扰信号时，扩展相消算法不能完全消除监视通道中的多径干扰信号，会造成多径干扰剩余，同时引入新的杂波．

时域干扰相消后的监视通道信号表示为

(5)

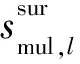
1.2 脉冲压缩

因为匹配滤波器是线性时不变系统，所以监视通道信号和参考信号可以转换到频域来进行脉冲压缩处理．相比于时域的卷积运算，频域的脉冲压缩运算量更小．脉冲压缩的输出信号为

对式(6)等号两边进行逆傅里叶变换，得到

(7)

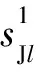
脉冲压缩结果表明，参考通道中的多径干扰信号与目标回波信号相匹配形成虚假目标，虚假目标与对应的真实目标位于同一多普勒单元内，虚假目标和真实目标的距离与时间差τn有关．这些虚假目标使得雷达系统的虚警概率升高，影响雷达系统的探测性能．因此，抑制参考通道中的多径干扰信号至关重要．

2 算法原理

笔者提出的改进恒模算法(Modified Constant Modulus Algorithm， MCMA)采用非因果的有限脉冲响应(Finite Impulse Response，FIR)滤波器构成，其输出为

(8)

其中，x(t)为滤波器输入向量，w(t)为滤波器权值向量，滤波器的阶数为2L+1．

根据最小化干扰原理，对滤波器权值的迭代过程进行优化，得到归一化最小均方(Normalized Least Mean Square， NLMS)算法:

(9)

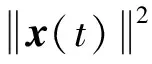
构造代价函数J(t)，在恒模算法的代价函数基础上增加信号高阶矩信息:

(10)

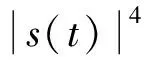
k阶均衡器输出的均值根据下式迭代计算:

(11)

对代价函数J(t)进行求偏导:

(12)

得到误差信号e(t)，即

(13)

3 仿真实验及结果分析

设置3组仿真实验来验证所提改进恒模算法的有效性，同时与传统恒模算法相比较，证明笔者所提算法具有更好的收敛性，可以更好地抑制参考通道中的多径干扰信号，消除虚假目标，改善外辐射源雷达系统的目标探测性能．

设外辐射源雷达利用非合作线性调频脉冲信号进行探测，其信号参数设置为：脉冲宽度为 300 μs，信号带宽为 2.5 MHz．设参考通道接收到的参考信号中包含直达波信号、多径干扰和通道噪声，其信号参数设置为：直达波信噪比为 35 dB，多径时延单元为[100，130]，干直比为 [-6 dB，-7 dB]．设监视通道接收到的参考信号中包含直达波信号、多径干扰信号、目标回波信号和通道噪声，其信号参数如表1所示．

表1 监视通道信号参数

表1中干直比为多径干扰与直达波信号比值(Multipath-to-Direct signal Ratios， MDR)．

以下3组仿真实验中，恒模算法和改进恒模算法的滤波器阶数为9．恒模算法迭代步长取0.01，改进恒模算法中α取0.2，β取2，加权常数ak取a1=2，a2=1，a3=2，a4=1．

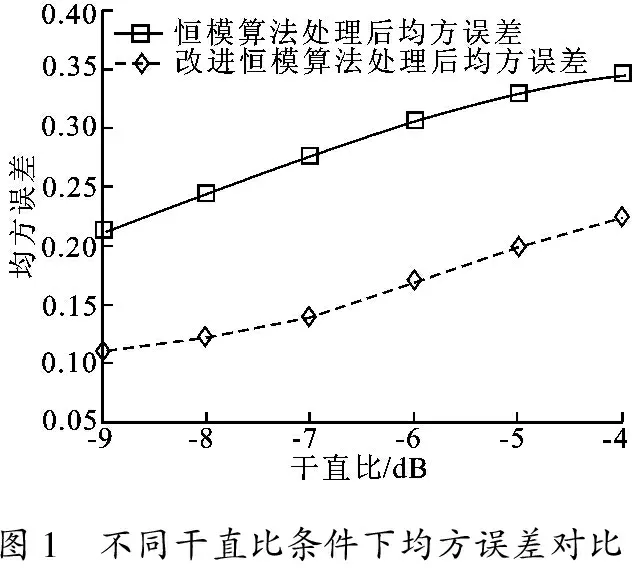
图1 不同干直比条件下均方误差对比

实验1 利用均方误差(Mean Square Error， MSE)来度量恒模算法的均衡效果，定量地分析比较恒模算法和改进恒模算法的均衡性能．

(14)

其中，M表示均衡器输出的均方误差．盲均衡器输出y(t)经过归一化处理，取γ2=1，得到仿真结果如图1所示．从图1中可以看出，恒模算法和改进恒模算法的均方误差随干直比增加而变大．在不同干直比条件下，笔者提出的改进恒模算法处理后的均方误差比恒模算法的更低，表明笔者提出的改进恒模算法具有更好的盲均衡性能．

实验2 实验1定量地比较了恒模算法和笔者提出的改进恒模算法的均衡性能．为了更加直观地比较两种算法的多径干扰抑制性能，本实验比较不同条件下脉冲压缩结果，结果如图2所示．盲均衡处理可以抑制参考通道中的多径干扰，但不能完全消除多径干扰．当监视通道杂波相消时，参考通道多径干扰所引入的杂波只是得到了抑制，没有被完全消除．图2(b)和图2(c)中多普勒维副瓣得到压低，但并没有被完全消除．

图2 脉冲压缩距离-多普勒图

图2(a)表示含有多径干扰的参考信号未处理的脉冲压缩结果．在图中可以看出，在真实目标1和2的多普勒单元内，分别出现两个虚假目标，虚假目标到真实目标的距离对应于多径干扰(相对于直达波)的时延，两个虚假目标是参考通道中两个多径干扰信号与监视通道中目标回波信号相匹配的结果．图2(b)表示参考信号经过恒模算法处理后的脉冲压缩结果．从图中可以看出，在图2(a)中虚假目标所在相同位置处，仍然出现虚假目标，与图2(a)中虚假目标相比，图2(b)中虚假目标峰值得到削弱，表明参考通道中的多径干扰经过恒模算法处理后得到一定程度的抑制．图2(c)表示参考信号经过改进恒模算法处理后的脉冲压缩结果．从图中可以看出，在图2(a)中虚假目标所在相同位置处没有明显峰值，虚假目标湮没在噪声之中，表明参考通道中的多径干扰经过改进恒模算法处理得到有效的抑制．本实验结果表明，改进恒模算法相比于恒模算法可以更好地抑制参考通道中的多径干扰．

实验3 实验2定性地比较了笔者提出的改进恒模算法和恒模算法的多径干扰抑制性能．改进恒模算法处理后虚假目标峰值较低，湮没在噪声之中．本实验定量地比较两种算法处理后真实目标-虚假目标峰值比，实验结果如图3所示．图3表示不同干直比条件下200次蒙特卡罗实验的结果．可以清晰地看出，笔者提出的改进恒模算法处理后的真实目标-虚假目标峰值比高于恒模算法．随着干直比的升高，恒模算法处理后的真实目标-虚假目标的峰值比降低，恒模算法的多径干扰抑制性能下降．而改进恒模算法多径干扰抑制性能不随干直比的升高而降低，处理后的峰值比更稳定．

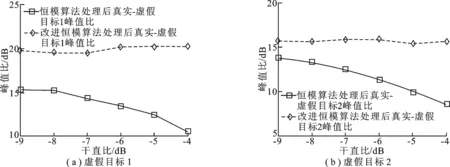
图3 真实目标与虚假目标峰值比

4 总 结

针对外辐射源雷达参考通道中含有多径干扰的问题，笔者提出了一种基于改进恒模算法的多径干扰抑制方法．含有多径干扰的参考信号会影响后续的干扰相消和匹配滤波．参考通道中的多径干扰与目标回波信号相匹配，在真实目标所在的多普勒单元内形成虚假目标，使得虚警概率升高，影响雷达系统的探测性能．笔者提出的改进恒模算法，在传统恒模算法的基础上优化其代价函数，加入信号的高阶矩信息，并且利用归一化最小均方算法对盲均衡器的权值向量进行迭代更新．仿真结果表明，相比于传统的恒模算法，笔者提出的改进恒模算法具有更好的收敛性，可以更好地抑制多径干扰，有效地消除多径干扰造成的虚假目标，改善了外辐射源雷达系统的探测性能．

[1] 王珏, 王俊, 武勇, 等. 缺失孔径下多基地外辐射源雷达成像算法[J]. 西安电子科技大学学报, 2016, 43(3): 25-30.

WANG Jue, WANG Jun, WU Yong, et al. Multistatic Passive Radar Imaging Algorithm for the Gapped Aperture[J]. Journal of Xidian University, 2016, 43(3): 25-30.

[2] COLONE F, BONGIOANNI C, LOMBARDO P. Multifrequency Integration in FM Radio-based Passive Bistatic Radar. PartⅠ: Target Detection[J]. IEEE Aerospace and Electronic Systems Magazine, 2013, 28(4): 28-39.

[3] COLONE F, BONGIOANNI C, LOMBARDO P. Multifrequency Integration in FM Radio-based Passive Bistatic Radar. Part Ⅱ: Direction of Arrival Estimation[J]. IEEE Aerospace and Electronic Systems Magazine, 2013, 28(4): 40-47.

[4] TAN B, WOODBRIDGE K, CHETTY K. Awireless Passive Radar System for Real-time through-wall Movement Detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(5): 2596-2603.

[5] ZAIMBASHI A. Multiband FM-based Passive Bistatic Radar: Target Range Resolution Improvement[J]. IET Radar, Sonar and Navigation, 2016, 10(1): 174-185.

[6] LV X Y, WANG J, WANG J. RobustDirection of Arrival Estimate Method in FM-based Passive Bistatic Radar with a Four-element Adcock Antenna Array[J]. IET Radar, Sonar and Navigation, 2015, 9(4): 392- 400.

[7] EDRICH M, SCHROEDER A, MEYER F. Design and Performance Evaluation of a Mature FM/DAB/DVB-T Multi-illuminator Passive Radar System[J]. IET Radar, Sonar and Navigation, 2014, 8(2): 114-122.

[8] ITO T, TAKAHASHI R, MORITA S, et al. Experimental Result of Passive Bistatic Radar with Unknown Transmitting Radar Pulse [C]//Proceedings of the 2013 European Microwave Week. Washington: IEEE Computer Society, 2013: 1767-1770.

[9] WANG Y, BAO Q, WANG D, et al. An Experimental Study of Passive Bistatic Radar Using Uncooperative Radar as a Transmitter [J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(9): 1868-1872.

[10] 朱昀, 王俊, 张各各, 等. 循环平稳弱目标回波信号的盲抽取方法[J]. 西安电子科技大学学报, 2016, 43(2): 52-57.

ZHU Yun, WANG Jun, ZHANG Gege, et al. Method for Blind Extraction of Echo Signal Based on Cyclostationarity[J]. Journal of Xidian University, 2016, 43(2): 52-57.

[11] SHAH S M, SAMAR R, NAQVI S M R, et al. Fractional Order Constant Modulus Blind Algorithms with Application to Channel Equalisation[J]. Electronics Letters, 2014, 50(23): 1702-1704.

[12] JIE S, YOU H, JIAN G, et al. Direct Wave Reconstruction of Non-cooperative Bistatic Pulse Radar Using Modified CMA+MMA Algorithm[C]//IET Conference Publications, no551cp. London: IET, 2009: 77648.

[13] COLONE F, CARDINALI R, LOMBARDO P, et al. Space-time Constant Modulus Algorithm for Multipath Removal on the Reference Signal Exploited by Passive Bistatic Radar[J]. IET Radar, Sonar and Navigation, 2009, 3(3): 253-264.