肺部ct的图像增强技术及opencv实现

李尧

(山西师范大学数计学院,山西临汾 041004)

1 引言

图象增强是数字图象处理领域中常用的一种技术。是通过放大图像中某些不易观察到细节,突出感兴趣的特征进而增强图像视觉效果的手段。在诸多领域有广泛的应用.如 航空航天,生物医学域,工业生产等。CT是一种医疗辅助图像,它的原理是根据人体不同的组织对X线的吸收率与透过率的不同,用灵敏度极高的仪器扫描人体,然后将测量所获取的数据输入电子计算机展示,协助医生诊断。OpenCV(Open Source Computer Vision Library)是一个基于BSD许可(开源)发行的跨平台计算机视觉库,提供了计算机视觉方面的很多通用算法。ITK(Insight Segmentation and Registration Toolkit)是美国国家卫生院下属的国立医学图书馆开发的一款开源的、跨平台的医学图像处理软件包,是一个影像分析扩展软件工具。本文通过itk对dcm(ct图像)进行解析,使用opencv对ct图像进行增强及可视化。

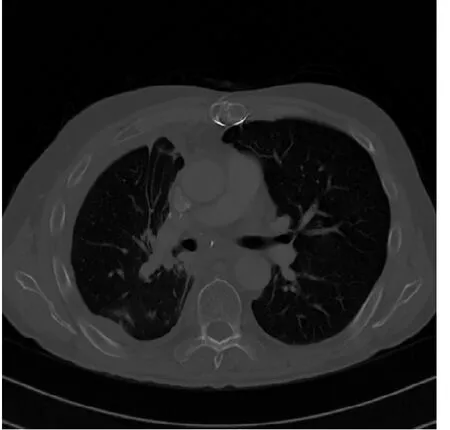
图1 原图像

图2 原图象的直方图

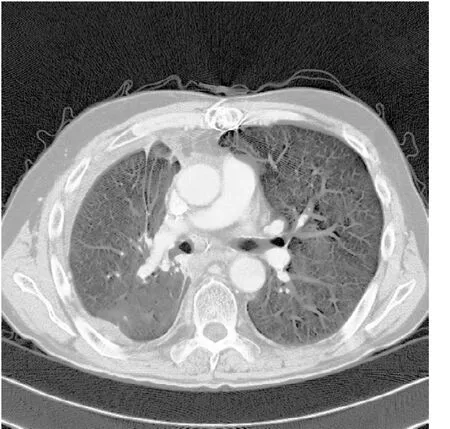
图3 直方图均衡化后的图像

2 图像增强

CT图像是由一定数目像素按矩阵排列所构成,其中每个像素存储的由黑到白的灰度值,是表示强度的标量。但通用计算机图片像素存储的表示RGB三通道强度的三维向量。出于精确度的考虑把ct图像映射入1个通道即可。

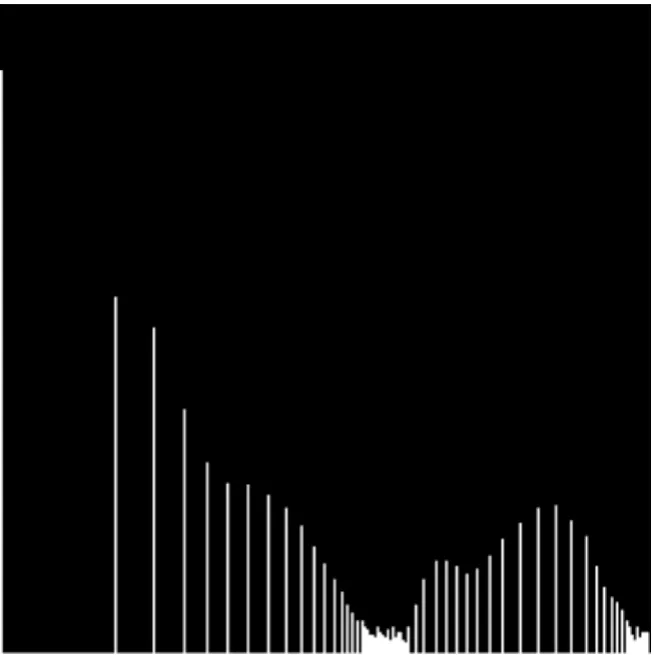
图4 均衡化后的直方图

2.1 基于直方图均衡化的图像增强

直方图是像素灰度值分布的函数,是按照灰度值的大小,统计其在数字图像中的所有像素中出现的频率,它表示图像中特定灰度值像素的个数。

基于直方图均衡化的图像增强的思想是通过扩大像素灰度值的范围。变换为均匀分布的形式,达到增强图像整体对比度,强调图像细节的效果。下图中图1为原图,直方图为图2。经过直方图均衡化后变为图3,直方图变化为图4。

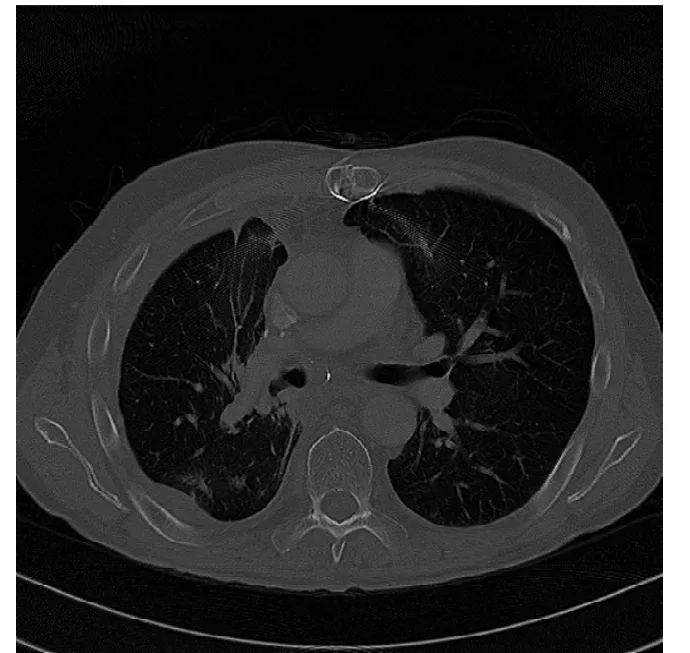
图5 拉普拉斯算子增强后的图像

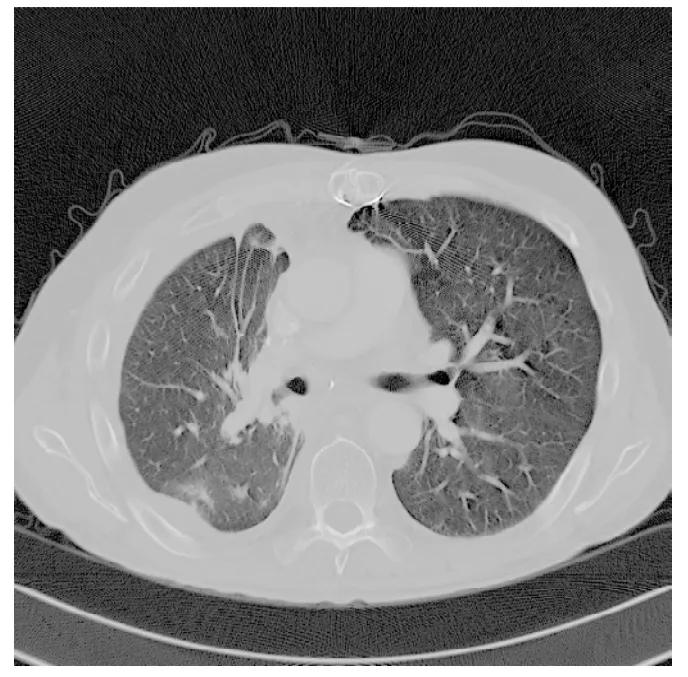
图6 对数变换后的图像

2.2 基于拉普拉斯算子的图像增强

拉普拉斯算子是二阶微分线性算子。与一阶微分相比,二阶微分算子有更强的边缘定位能力。用拉普拉斯运算就会使图像中位于较暗的区域中的亮点变得更亮。达到突出图像中的孤立线或端点的目的。并且拉普拉斯算子具有旋转不变性。

使用二阶微分算子的法通常是先定义算子的离散形式,然后根据离散形式生成滤波模板,利用这个与目标图像卷积。

二维图像的拉普拉斯算子是各向同性的二阶导数,定义为:

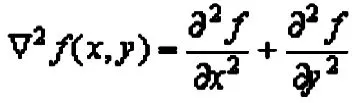
经过化简得到:

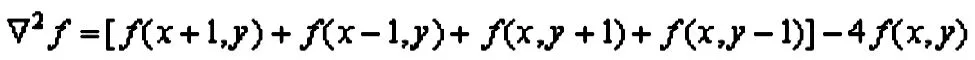
即取上下左右四个像素点的灰度和减去本身灰度的4倍。拉普拉斯算子可增强图像中灰度突变的区域,削弱灰度变化缓慢的区域。因此,可先对原图像进行拉普拉斯算子处理,产生描述灰度突变的图像,再将生生的图像与原始图像叠加。经过以上步骤生成的图像。在产生拉普拉斯锐化效果的同时又能保留背景信息。图像中的各灰度值得到保留,使灰度突变处的对比度得到增强,最终结果是在保留图像背景的前提下,突现出图像中的细节信息。

本文使用中心为5的8邻域拉普拉斯算子与图像卷积。图5为增强后的图片。

2.3 基于对数Log变换的图像增强

对数曲线在值较低的区域斜率大,在值较高的区域斜率较小,所以图像经过对数变换后,较暗区域的对比度将有所提升,所以就可以增强图像的暗部细节。

对数变换可以扩展图像的灰度值低的部分,强调显示低灰度部分更多的细节,从而达到增强图像的效果。

数变换公式如下:

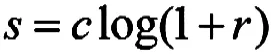
其中c为常数,r>=0。

图6为增强后的图片。

3 结语

基于直方图均衡化,基于对数Log变换增强方式,可以增强细节的显示能力,但会引起图像背景失真和放大噪声的副作用。基于拉普拉斯算子的图像增强在增强细节的同时不会引起背景图像的失真,对于医疗背景下图像增强效果较好。

[1]张静.基于JPEG的图像编辑与增强方法的研究与设计[D].北方工业大学,2014.

[2]钱松,李建荣.应用拉普拉斯算子设计高通滤波器进行图像增强分析[J].软件导刊,2011,10(12):158-159.

[3]杨晶晶,苟吉祥.常用CT图像增强方法研究[J].硅谷,2011,(19):97+125.