MMC阀子模块IGBT损耗与结温计算

殷冠贤, 朱铭炼， 谢晔源，姜田贵

(南京南瑞继保电气有限公司，江苏 南京 211102)

0 引言

随着电力系统规模的日益扩大，统一潮流控制器(unified power flow controller，UPFC)被广泛应用于柔性交直流输电等场合。目前除了已投入使用的南京西环网UPFC示范工程，还有苏南UPFC工程等建设中的工程，对有效缓解能源负荷分布不均问题，增强我国电网构架起到积极的作用，获得了良好的社会效益和经济效益[1-9]。

UPFC换流阀使用最具有前景的模块化多电平换流器(modular multilevel converter,MMC)，其子模块具有承受高电压、大电流的特点，而子模块绝缘栅双极型晶体管(insulated gate bipolar transistor，IGBT)的损耗和结温理论计算方法对其在MMC工程化应用中的热设计和选型非常重要。IGBT在MMC在稳态运行过程中的损耗计算是其结温计算的关键。目前计算MMC损耗主要有两种计算方法，第一种是利用仿真软件搭建模型来计算实时功率损耗，依靠模型搭建的准确性[10]，另一种是利用解析经验公式对MMC换流阀损耗进行计算，此法具有较大的优势[11-16]。

文中首先对MMC稳态运行时模块的电应力进行分析，其次，设计MMC阀子模块IGBT的损耗和结温的理论计算方法，最后进行了试验验证。

1 MMC工作原理

MMC拓扑如图1所示，MMC阀由3个相单元组成，每个相单元包含2个桥臂，每个桥臂包含一个桥臂电抗器L0和N个子模块(sub module，SM)。MMC在运行时，每个相单元根据调制电压决定上下桥臂投入的子模块数，为了持续输出稳定的直流电压Udc，每个相单元上下桥臂投入的子模块数总和固定为N。MMC子模块一般采用半桥拓扑，包含2个开关器件IGBT1(T1)和IGBT2(T2)，分别带有反并联寄生二极管D1和D2，开通子模块的T1，即投入，开通子模块的T2，即切出。

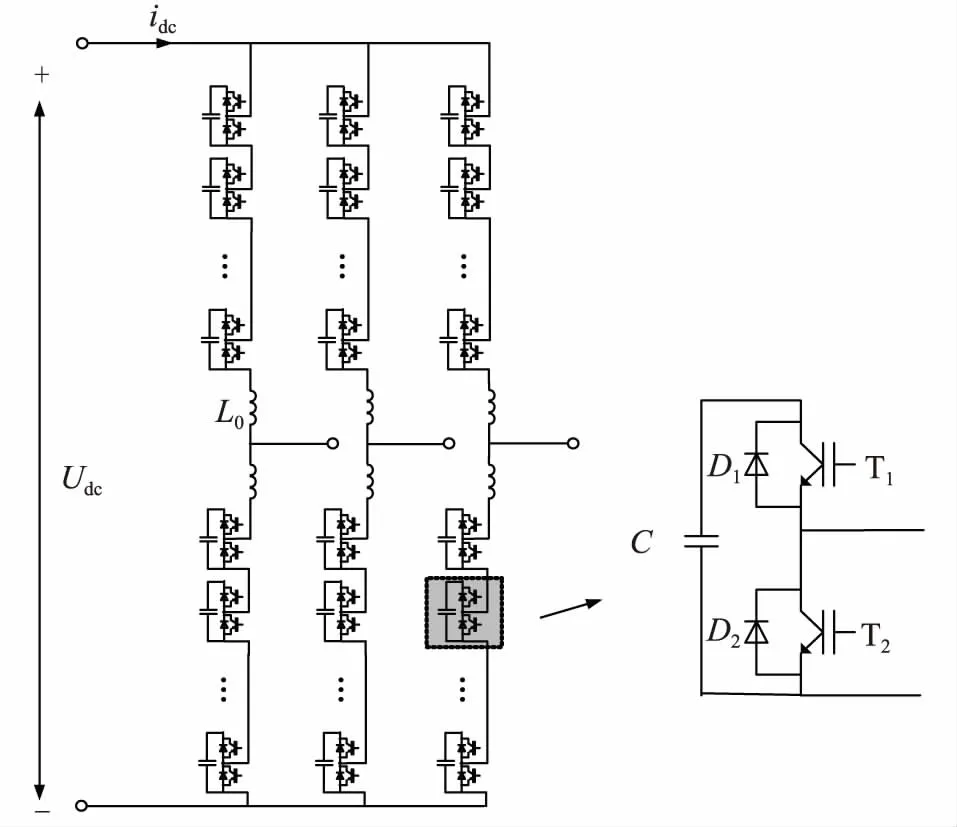
图1 MMC拓扑Fig.1 Topology of MMC

根据能量守恒，桥臂电流是直流叠加交流的交直流变量。MMC的6个桥臂具有对称性，以A相上桥臂为例，桥臂的电压和电流为:

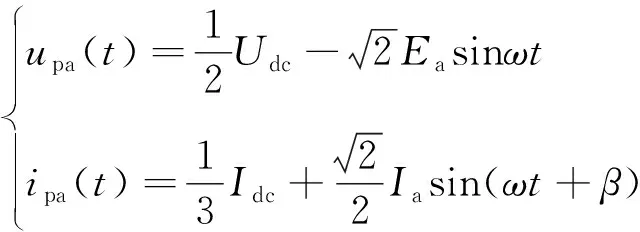
(1)

式中：Udc为直流电压；Idc为直流电流；Ea为相单元内部电动势有效值；ω为角频率；β为upa和ipa的相位差；Ia为交流侧电流有效值。

2 MMC阀子模块IGBT损耗分析与计算

MMC阀的损耗主要由子模块的损耗和桥臂电抗器的损耗构成。子模块的损耗对MMC阀损耗占比最大，而子模块的损耗中占比最重的是其开关器件IGBT的损耗，通过IGBT的损耗分析可以进一步得到MMC阀稳态运行时IGBT的结温。

之前的研究都是利用子模块的电压和电流去计算子模块IGBT的损耗，但是子模块的损耗不仅要考虑子模块的电流和电压，还要考虑子模块投入和切出的时间，而子模块投入或者切出又受电容均压控制等影响，所以很难得出一个子模块准确的投入和切出的时域模型。由于每个桥臂中所有子模块特性的趋向具有一致性，所以先计算MMC桥臂所有子模块的通态总损耗，然后再得出单个子模块中各个开关器件的通态损耗。

由于MMC 6个桥臂具有对称性，以A相为例，由式(1)可知A相上桥臂投入的子模块数为：

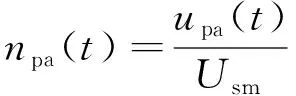
(2)

式中：Usm为子模块电容电压。

另外，电流在子模块内部的流向由触发信号和桥臂电流的方向决定，定义桥臂电流从交流侧流向直流侧为正方向。

触发信号波形如图2所示，桥臂电流大于零时，若子模块处于投入状态，则电流流过T1；若子模块处于切出状态，则电流流过D2。桥臂电流小于零时，若子模块处于投入状态，则电流流过D1；若子模块处于切出状态，则电流流过T2。

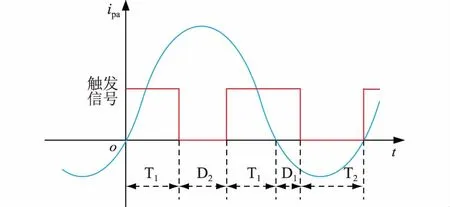
图2 器件导通时间区间Fig. 2 The operating regions of switching device

可知A相上桥臂所有子模块中的T1总的通态瞬时损耗功率为：

(3)

式中：Uce为T1和T2的通态压降；Rce为T1和T2的通态电阻。

A相上桥臂所有子模块中的IGBT1反并联二极管D1总的通态瞬时损耗功率为：

(4)

式中:Ud为D1和D2的通态压降；Rd为D1和D2的通态电阻。A相上桥臂所有子模块中的T2总的通态瞬时损耗功率为：

(5)

A相上桥臂所有子模块中的IGBT2反并联二极管D2总的通态瞬时损耗功率为：

(6)

同一个桥臂中所有的子模块损耗具有趋向一致性，则A相上桥臂每个子模块中的T1、D1、T2和D2的通态损耗为：

(7)

式中：PT1Vsm为T1的通态损耗；PD1Vsm为D1的通态损耗；PT2Vsm为T2的通态损耗；PD2Vsm为D2的通态损耗。

除了IGBT通态损耗，MMC阀子模块的每次投切使得IGBT还存在单次开通损耗Eon、单次关断损耗Eoff和反并联二极管的单次反向恢复损耗Erec，它们和IGBT集电极电流Ic、二极管电流IF的关系如图3所示。

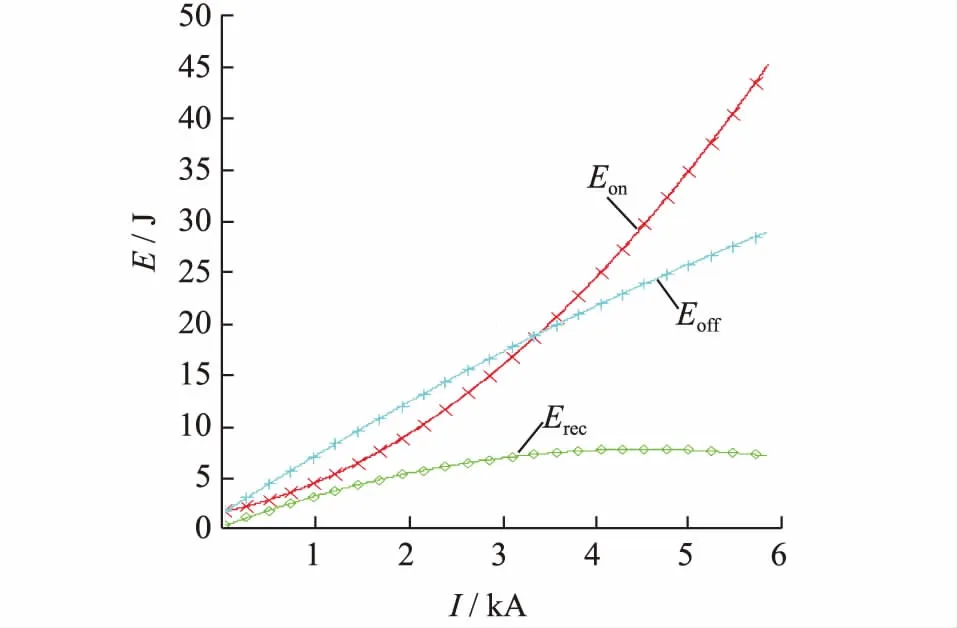
图3 Eon，Eoff和Erec与Ic，IF的关系Fig. 3 The relationship between Eon, Eoff, Erec and Ic,IF

可以使用曲线拟合的方法[17]得到Eon，Eoff和Erec与Ic，IF的函数关系，如式(8)所示：

(8)

式中：aTon，bTon，cTon分别为IGBT开通损耗的拟合系数；aToff，bToff，cToff分别为IGBT关断损耗的拟合系数；arec，brec，crec分别为反并联二极管反向恢复损耗的拟合系数。

由式(8)的周期积分与周期时间的比值得到：

(9)

式中：PT1on为T1的开通损耗；IT1rms为T1的电流有效值；IT1avg为T1的电流平均值；fs为开关频率；PT1off为T1的关断损耗。

同理可得IGBT2的开关损耗：

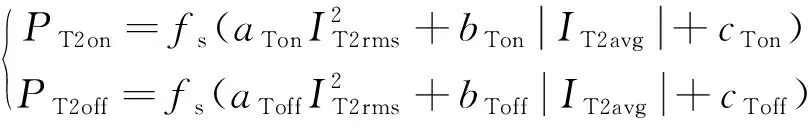
(10)

式中：PT2on为T2的开通损耗；IT2rms为T2的电流有效值；IT2avg为T2的电流平均值；PT2off为T2的关断损耗。

反并联二极管的反向恢复损耗：

(11)

式中：PD1rec为D1的反向恢复损耗；PD2rec为D2的反向恢复损耗；ID1rms为D1的电流有效值；ID1avg为D1的电流平均值；ID2rms为D2的电流有效值；ID2avg为D2的电流平均值。

可得子模块的T1、D1、T2和D2的总损耗：

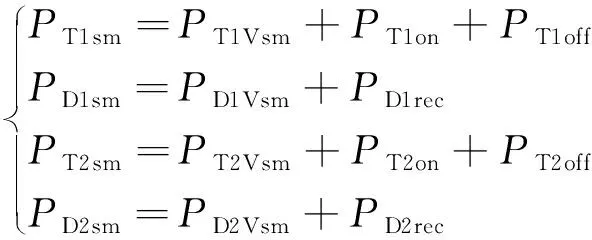
(12)

式中:PT1sm为T1的总损耗；PD1sm为D1的总损耗；PT2sm为T2的总损耗,PD2sm为D2的总损耗。

3 MMC阀子模块IGBT结温分析与计算

在MMC阀稳态运行时IGBT的损耗会在IGBT累计转化为热量，最终表现为IGBT的结温，计算IGBT结温计算可以通过IGBT等效热阻抗来计算。根据IGBT器件手册查得等效热阻抗，以5SNA 3000K452300型IGBT为例，其热阻抗曲线如图4所示。

(13)

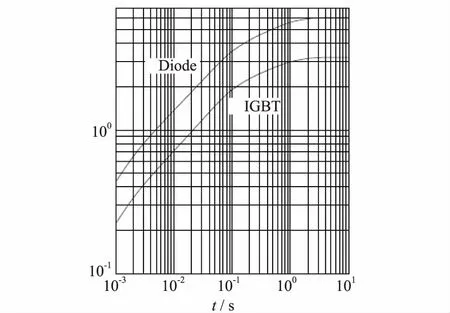
图4 IGBT热阻抗曲线Fig. 4 Thermal impedance curve of IGBT

IGBT的结温估算模型如图5所示，图中Zth(c-h)为散热器和IGBT外壳基板间的热阻。

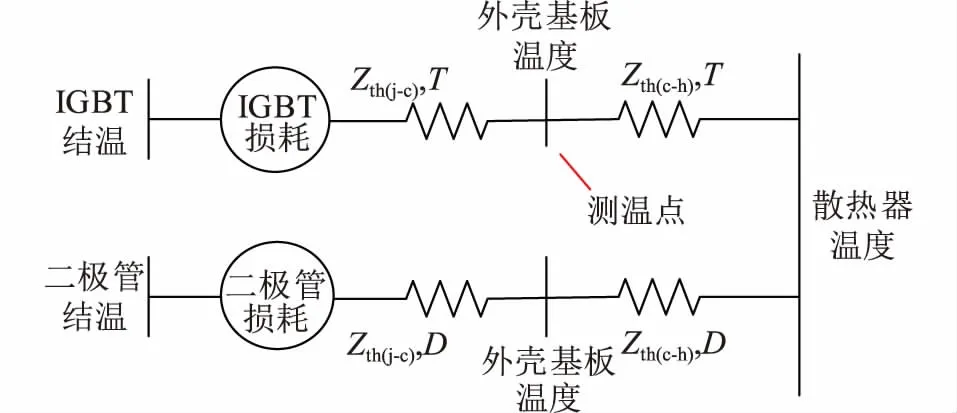
图5 结温估算模型 Fig.5 Temperature estimation model

为了避免散热器和IGBT外壳基板间的热阻的误差影响，更准确地计算IGBT的结温，测温点选择在IGBT1外壳基板。假设Tb1为IGBT1外壳基板的温度，Tb2为IGBT2外壳基板的温度,则子模块的IGBT1和IGBT2的最高结温TT1，TT2分别为：

(14)

4 试验验证

为了验证所给出的计算方法有效可行，在两端MMC背靠背试验系统中进行了试验验证，试验系统结构如图6所示。

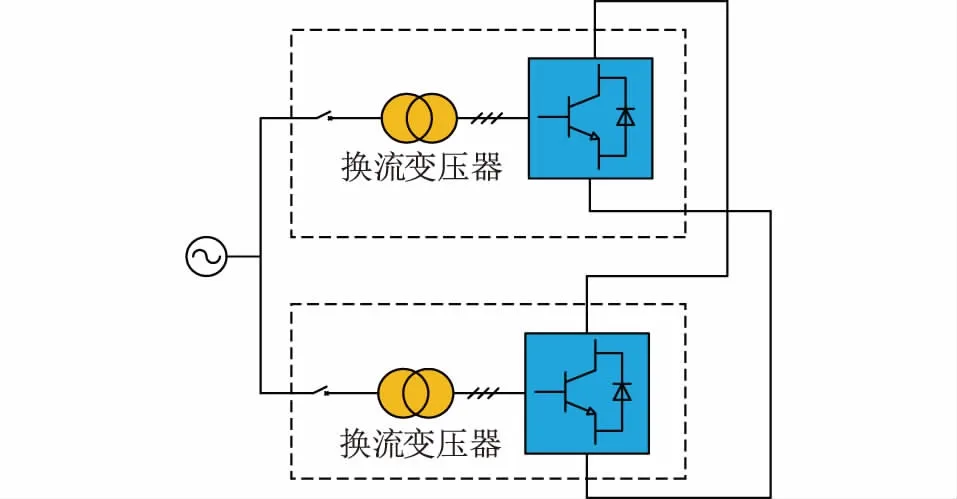
图6 MMC背靠背试验系统Fig. 6 MMC back-to-back system

试验参数如表1所示，IGBT选择5SNA3000K452300型IGBT模块。试验波形如图7所示。

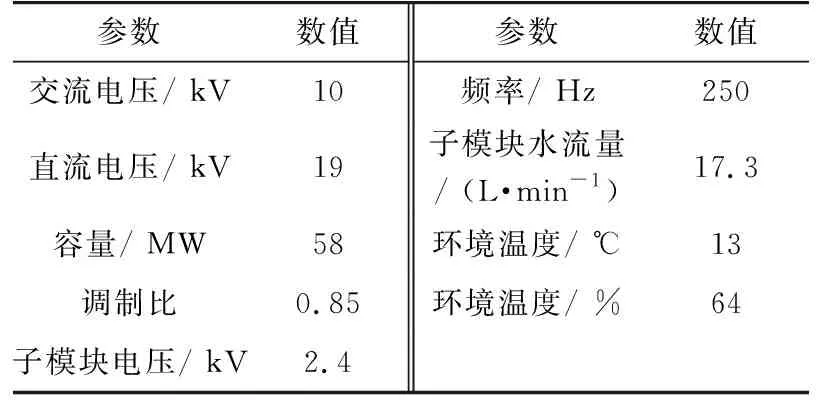
表1 MMC背靠背系统试验参数Tab. 1 Test parameters of MMC back-to-back system

图7 试验波形(对应2100 A)Fig. 7 The test waveform in 2100 A

稳态试验电流波形如图7(a)所示，最大稳态试验电流有效值Ipa=2.107 kA。在IGBT器件手册查得稳态电流为2.100 kA时，T1和T2的通态压降Uce=1.5 V，T1和T2的通态电阻Rce=0.000 717，D1和D2的通态压降Ud=1.75 V，D1和D2的通态电阻Rd=0.000 417。按照文中损耗计算方法，将试验电流及IGBT参数代入式(12)，计算出子模块两个IGBT总的理论计算损耗为9.630 kW，其中IGBT1(T1和D1)的计算损耗为2.497 kW，IGBT2(T2和D2)的计算损耗为7.133 kW。

子模块进出水温差试验波形如图7(b)所示，可见稳态时子模块进出水温差稳定在8 ℃，通过冷却介质水的比热容来计算子模块的总损耗为9.688 kW，因为子模块的损耗还包括了板卡和其他元器件等损耗，所以子模块的计算损耗会比实际的损耗小。表2为不同电流时理论计算损耗和实际损耗的比较，两者较为接近。

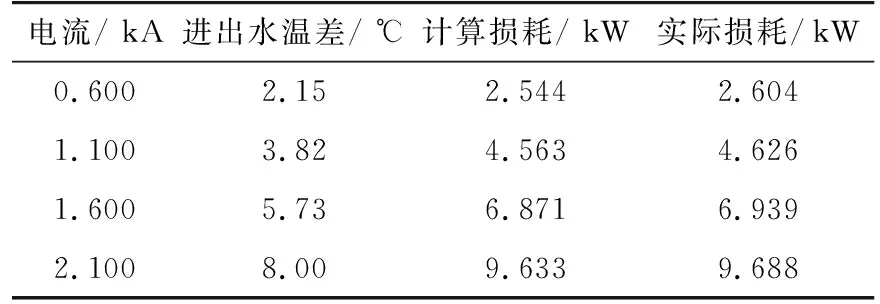
表2 理论计算损耗和实际损耗的比较Tab. 2 Comparison of theoretical calculation loss and actual loss

由于稳态时IGBT2的损耗较高，所以子模块内部IGBT2的结温是最高的。试验时IGBT内部的结温无法测量，可以结合图7(c)所示的IGBT2的底板温度，由式(14)计算IGBT2的结温约为78 ℃，如果试验时环境温度为45 ℃，则IGBT2的结温会达到110 ℃左右，但还在IGBT温度安全范围内。

5 结语

文中对MMC模块稳态应力进行了分析，给出了一种MMC子模块IGBT损耗和结温的理论计算方法，将理论计算结果与试验结果进行比较，考虑到理论计算存在一定的偏差，结果证明了所给出的计算方法有效可行。

参考文献：

[1] 徐 政，屠卿瑞，管敏渊，等． 柔性直流输电系统[M]． 北京：机械工业出版社，2013：1-25．

XU Zheng，TU Qingrui，GUAN Minyuan，et al． Voltage source converter based hvdc power transmission systems[M]． Beijing：China Machine Press，2013：1-25．

[2] 管敏渊，徐 政． MMC型柔性直流输电系统无源网络供电的直接电压控制[J]． 电力自动化设备，2012，32(12)：1-5．

GUAN Minyuan，XU Zheng． Direct voltage control of MMC based VSC-HVDC system for passive networks[J]． Electric Power Automation Equipment，2012．32(12)：1-5．

[3] 徐 政，陈海荣． 电压源换流器型直流输电技术综述[J]． 高电压技术，2007，33(1)：1-10．

XU Zheng，CHEN Hairong．Review and applications of VSC HVDC[J]． High Voltage Technology，2007，33(1)：1-10．

[4] 汤广福． 基于电压源换流器的高压直流输电技术[M]． 北京：中国电力出版社，2010．

TANG Guangfu．Voltage source converter based hvdc power transmission technology[M]．Beijing： China Electric Power Press，2010．

[5] 管敏渊，徐 政. MMC型VSC-HVDC系统电容电压的优化平衡控制[J]． 中国电机工程学报，2011,31(12)：9-14．

GUAN Minyuan，XU Zheng．Optimized capacitor voltage balancing control for modular multilevel converter based VSC-HVDC system[J]．Proceedings of the CSEE，2011，31(12)：9-14．

[6] 刘建涛，王治华，王 珂． 不同结构电压源换流器损耗对比分析[J]． 电力系统保护与控制，2013，41(6)：105-110．

LIU Jiantao,WANG Zhihua．WANG Ke．Comparative analysis of losses of voltage source converters with differentstructures[J]．Power Systems Protection and Control，2013，41(6)：105-110．

[7] ROHNER S，BERNET S，HILLER M，et a1． Modulation，losses，and semiconductor requirements of modular multilevel converters[J]．IEEE Trans on Industry Electronics，2010，57(8)：2633-2642．

[8] TU Qingrui, XU Zheng,XU Lei. Reduced switching-frequency modulation and circulating current suppression for modular multilevel converters [J ]. IEEE Trans on Power Delivery,2011,26(3):2009-2017.

[9] ZHANG Y,ADAM G P,LIM T C,et al. Analysis of modular multilevel converter capacitor voltage balancing based on phase voltage redundant states [J ]. IET Power Electronics,2012,5(6):726-738.

[10] 屠卿瑞,徐 政. 基于结温反馈方法的模块化多电平换流器高压直流输电阀损耗评估[J]. 高电压技术,2012,38(6):1506-1512.

TU Qingrui, XU Zheng. Dissipation analysis for MMC-HVDC based on junction temperature feedback method[J]. High Voltage Engineering, 2012,38(6):1506-1512.

[11] 李 强，贺之渊，汤广福，等． 新型模块化多电平换流器空间矢量脉宽调制的通用算法[J]． 电网技术，201l，35(5)：59-64．

LI Qiang，HE Zhiyuan，TANG Guangfu，et a1． A generalized algorithm of space-vector PWM for a new type of modular mul-ti-level converter[J]． Power System Technology，201l，35(5)：59-64.

[12] 宋 强，刘文华，李笑倩，等． 模块化多电平换流器稳态运行特性的解析分析[J]． 电网技术，2012，36(11)：198-204．

SONG Qiang，LIU Wenhua，LI Xiaoqian．et al．An analysis method for analysis on steady．state operating characteristics of roodular muhilevel converter[J]．Power System Technology,2012,36(11)：198-204．

[13] TOMAS M, HANS P N, STAFFNA N. Loss comparison of different sub-module implementations for modular multilevel converters in HVDC applications[J]. EPE Journal, 2012, 22(3):32-38．

[14] YANG L, ZHAO C, YANG X. Loss calculation method of modular multilevel HVDC converters[C]∥Electrical Power and Energy Conference. IEEE, 2011:97-101.

[15] 赵 昕，赵成勇，李广凯，等． 采用载波移相技术的模块化多电平换流器电容电压平衡控制[J]． 中国电机工程学报，2011，31(21)：48-55．

ZHAO Xin，ZHAO Chengyong，LI Guangkai，et a1．Submodule capacitance voltage balancing of modular multilevel converter based on carrier phase shifted SPWM technique[J]．Proceedings of the CSEE,2011,31(21)：48-55．

[16] XU D, LU H, HUANG L, et al. Power loss and junction temperature analysis of power semiconductor devices[C]∥ Industry Applications Conference, 1999. Thirty-Fourth Ias Meeting. Conference Record of the. IEEE, 1999:729-734．

[17] 李 强，庞 辉，贺之渊,等． 模块化多电平换流器损耗与结温的解析计算方法[J]. 电力系统自动化,2016,40(4):85-91.

LI Qiang, PANG Hui, HE Zhiyuan. Analytic calculating method for loss and junction temperature of modular multilevel converter [J]. Automation of Electric Power Systems ,2016,40(4):85-91.