双进口引水式电站水力过渡计算分析

燕军乐，吴亚军，万继伟

0 引言

我国西南地区的中小水电站多采用引水式电站，水电站的水力过渡问题不可避免，涉及水力学、水轮机和电气系统的相互影响和相互制约，关乎引水系统的优化设计和水电站的安全运行[1]，因此往往在水电站建设前期，需要对水电站的水力过渡过程进行论证。其目的主要是论证压力管道系统的合理性，通过确定最危险工况下有压引水系统最大、最小内力压力等，寻求优化的体型、合理的工程措施、最佳的调节规律，把过渡过程造成的危险减小到最低程度[2][3]。

对于引水式电站而言，目前采用较多的为单进水口、一管多机的模式。但对于单一进水口水电站，当引流量不能满足设计发电要求，而要加大水电站发电量或者要求提高机组出力时，可采用多进口或增加水电站进水口的工程措施来实现[4]。在研究计算水电站水力过渡的过程时，将存在大量的非线性问题，较为复杂。对于单一进口电站的水力过渡已有大量研究，本文则主要以双进口引水式电站为计算模型，对双进口水电站水力过渡过程进行数值模拟研究。

1 电站引水系统形式和基本参数

本文以某双进口引水电站为例进行研究，采用双进口、一管两机布置形式，为无调压井冲击式电站。引水管道概化为圆形管道，分上游支管、主压力管道和下游岔管三部分，管道系统布置示意图如图1所示，管道系统特性参数见表1。

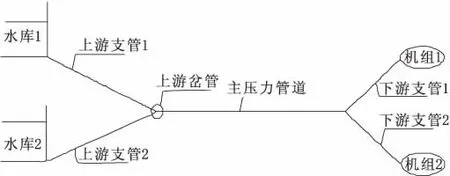
图1 管道系统布置简图

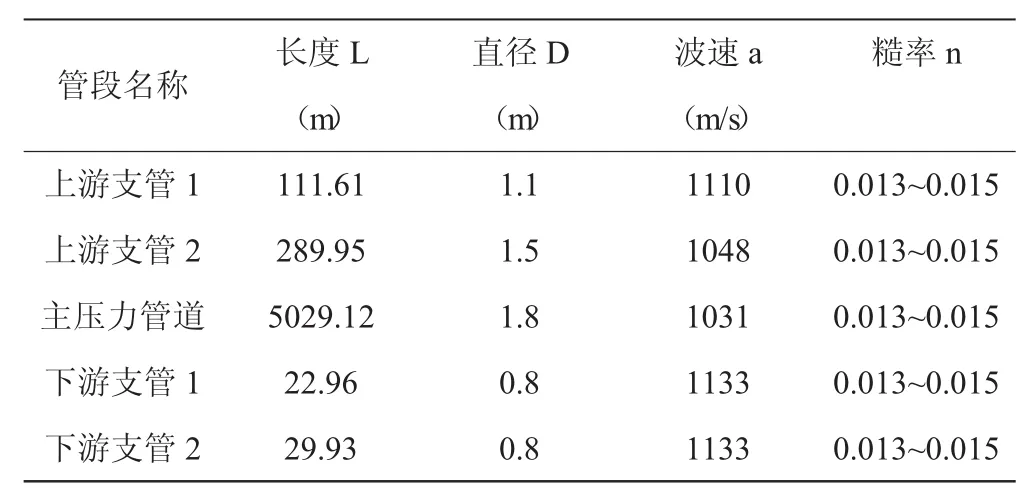
表1 管道系统特性参数表

进水口为高程不同的两个底格栏栅坝，其中水库1设计水位为3388.03 m，水库2设计水位为3389.1 m；机组安装高程为3014.5 m；其对应的静水头分别为373.53 m和374.6 m，机组采用直线关闭。水电站设计总装机容量为22MW，引用流量为7.6 m3/s，额定水头为348 m。

2 数值计算

有压引水系统水力过渡过程大波动的控制方程主要为有压引水系统非恒定流的圣维南方程组。

2.1 管道瞬变流计算

管道瞬变流计算基本方程为运动方程和连续方程，即圣维南方程组，采用特征线法求解。

运动方程：

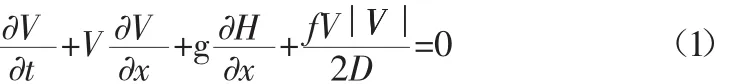
连续方程：

式中：H为测压管水头压头；V为断面平均流速；x为沿管轴线的距离；D为管道断面直径；a为水击波传播速度；g为重力加速度；t为时间；α为管道倾斜角；f为摩阻系数。由于引水隧洞平均坡度为0.07，通过计算法分析，管道倾斜对计算影响很小，因此本次计算时均忽略此项。由方程（1）、（2）可得普遍应用的特征线方程。

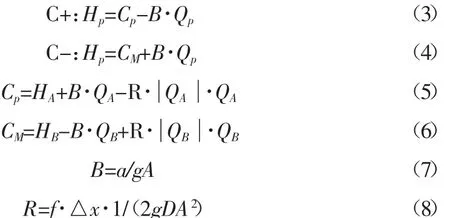
式中：HA、QA分别为t-Δt时刻管段第i-1节点处的压头和流量；HB、QB分别为t-Δt时刻管段第i+1节点处的压头和流量；Δx为相邻两节点的距离；R为阻力系数；CP，CM分别与t-Δt时刻的压头和流量有关，对t时刻是已知量。

2.2 计算方法

双进口引水式电站不同于单进口，在进行水力过渡过程计算时，需已知上游两条支线管道的初始流量Q1与Q2。本次计算采用Fortran语言进行计算，先采用试算法，假设两个支管内的流量Q1与Q2，然后沿上游支管1和上游支管2至上岔管分别列能量方程和整体连续性方程。在岔管的节点上，根据两个分支的测压管水头相等，修正两个支管的流量，进一步调整岔管节点上两个分支的测压管水头，使其差值在一定误差范围内，从而确定两个支管的流量和岔管节点处的测压管水头，计算框图如图2所示。

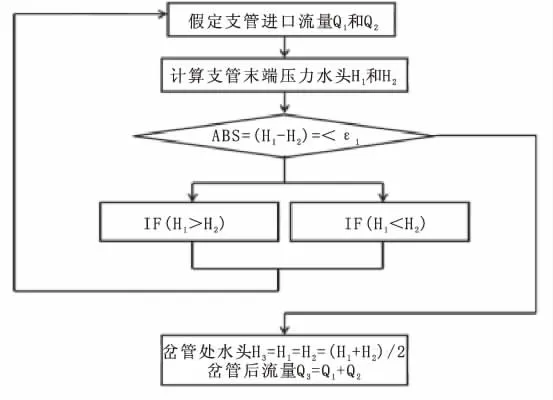
图2 计算框图

3 成果分析

3.1 低水位水库进水口处逆流的有关问题

大波动两台机组同时甩额定负荷数值模拟时，发现约在关闭时间五分之三时，较低库水位进口处开始出现了逆流现象。

3.1.1 逆流量与机组关闭时间的关系

为了验证机组关闭时间与逆流量的关系，分别计算了原始条件下机组关闭时间为30 s、40 s和60 s时，两支管进口处水流流量变化情况，变化曲线如图3所示。可以看出，从机组完全关闭时起，受水击波来回反射影响，进水口的逆流量围绕某一值上下浮动振荡。逆流量的变化周期与幅值受机组关闭时间影响明显，当关闭时间越长，逆流量浮动周期变长，浮动值减小。

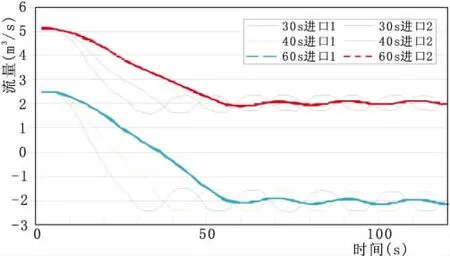
图3 不同进水口水流流量随机组关闭时间变化曲线

3.1.2 逆流量随支管管道参数的敏感性分析

以机组关闭时间30 s为例，进行逆流量随支管管道参数变化的敏感性分析。

以表1中管径参数进行初始条件下计算的流量随时间变化曲线如图4所示。可知，在机组关闭后，两个进水口通过叉管连通，由于夹杂着水击波，进水口流量产生波动现象，且两进水口流量变化曲线呈反对称分布。表现为当进水口2流入水量最大时，进水口1出水量最小；当进水口2流入流量最小时，进水口1流出水量最大；此时其流量均在2.04 m3/s左右浮动。

为测试支管长度对流量变化影响的敏感性，改变支管1长度，使其分别为111.61 m、220 m和289.95 m，其他支管和总管的长度以及所有管的管径均不变，支管1进口处逆流量随时间变化曲线如图5所示。可以看出，进口的逆流量与支管的管道长度无关，但逆流周期随着管道长度的增加而略有增加。

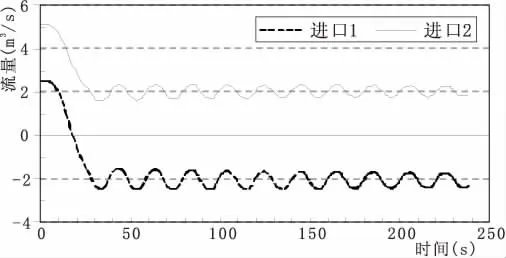
图4 初始条件下流量随时间变化曲线

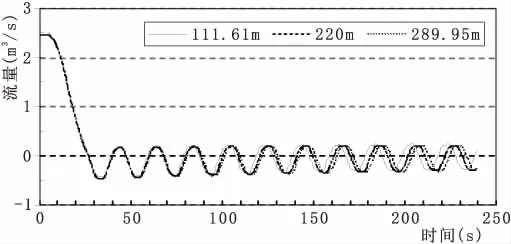
图5 不同长度时支管1进口水流量变化曲线

当支管1采用同支管2相同管径和长度，其他管径和长度均不变时，两进水口流量随时间的变化曲线如图6所示。可以发现，在机组关闭以后，两进水口流量变化曲线也呈反对称分布，此时其流量均在2.24 m3/s左右浮动，略大于初始条件状态（图4）。

对上支管1与上支管2的管道参数（管径和管道长度）交换后，两进水口流量随时间变化曲线如图7所示。通过该参数条件下的计算结果与初始条件下的结果（图4）对比，可见，当高库水位采用小管径、低库水位采用大管径时（图7），较高库水位对应大管径、低库水位对应小管径时，平衡时逆流量的值略小，前者约在1.68 m3/s左右浮动。

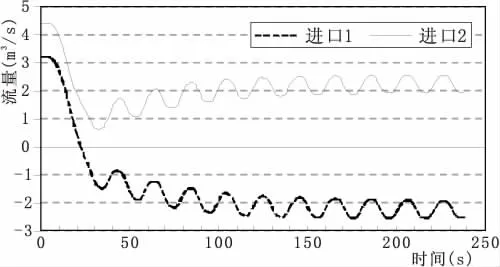
图6 上支管1管道参数同上支管2时进口流量随时间变化曲线

图7 上支管1与支管2参数交换后进口流量随时间变化曲线

3.2 上游岔管瞬间压降

当进行大波动1台→2台或1台→2台→0台此类增负荷工况模拟时，在水击波第一次传到上游岔管处时（约第5秒），产生压力瞬间下降的情况，其中上游岔管压力随时间变化曲线如图8所示。可以看出，机组开启时间在30 s、40 s和60 s时，岔管处压力随时间变化趋势基本一样，随着时间的推移，压力降的波动幅值减小，在足够时间后（约80s）压力逐渐趋于稳定。第一次水击波传到上游岔管处时的压降值大小与机组开启时间无关，而其后的压力值与机组开启时间有关，且开启时间越短，其后的压力值相对较小。

对上游支管管径进行改变后进行计算，可得上游支管参数对岔管处压力变化的影响，压力变化曲线如图9所示。可以看出，随着支管管径的增大，上游岔管处的第一次水击波来临时的瞬时压降值减小，且这种现象在各体型各水位下均出现，与管径和水位无关。这种压降值虽然有时不是很大，但是为瞬时压降，易引起管道的振动等不良情况的发生。

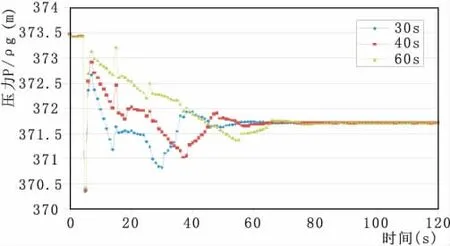
图8 不同机组开启时间时上游岔管压力随时间变化曲线

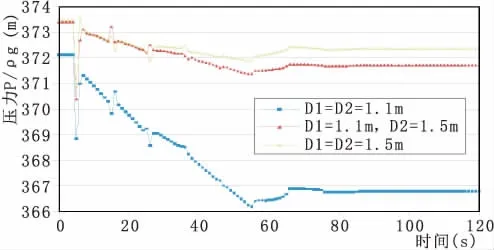
图9 不同管径时上游岔管压力随时间变化曲线

不同上游水位时岔管处压力变化如图10所示，水位对岔管处压力大小的影响，仅体现在上游水位间的差值上，而随时间的压力降幅度与上游水位无关。

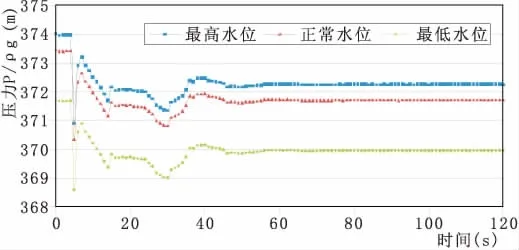
图10 不同水位时上游岔管压力随时间变化曲线

4 结论

本文对双进口引水式电站的水力过渡进行了计算分析，主要成果有：

1）在机组关闭时间五分之三时，进口处开始出现逆流现象，逆流量随水击波的来回反射上下浮动，浮动值周期和幅值受机组关闭时间影响明显，关闭时间越长，浮动周期变长，浮动值减小。

2）通过计算可知，进口逆流量大小与支管的管道长度无关，但逆流周期随管道长度的增加而略有增加；增大管径和管道长度时逆流量会略有增大；高库水位采用小管径、低水位采用大管径时，要较低库水位对应小管径、高库水位对应大管径时，平衡时逆流量的值略小。

3）进行增负荷计算时，当机组关闭时，上游分岔处因水击波的到达发生瞬时压降，且压力降的大小与开启时间无关。

[1]张鹏.水电站水力过渡过程的数值仿真及参数优化[J].武汉：武汉大学水利水电学院，2007.

[2]林劲松，巨江，诸亮，吕宏兴.水电站水力过渡过程仿真计算的工程应用.水力发电学报[J].2010，2.29(1):31-37.

[3]巨江.工程水力学数值仿真与可视化[M].北京：中国水利水电出版社.2010.10.

[4]王魁元.浅谈双洞引水式水电站[J].东北水利水电.1992.（04）：8-10.