基于遗传算法的复合材料平尾优化设计方法研究

徐合良，黄钦儿

(中国直升机设计研究所，江西 景德镇 333001)

0 引言

随着材料技术的进步和直升机性能需求的不断提高，先进复合材料在直升机上的应用和需求越来越大，先进复合材料具有低密度、高比强度、高比模量以及可设计性等诸多优点，已成为航空航天各类飞行器的主要结构材料。在国外，主要的军、民用直升机，如PAH-2、RAH-66和NH-90等，均大量采用了先进复合材料[1]。

近年来，国内外对直升机复合材料的各个部件研究较多。刘诗璋[2]对直升机复合材料平尾进行了全面的力学分析，得出了平尾的应力应变分布。杨建灵等[3]对复材旋翼铺层设计提出了优化方案，提高了复合材料建模的效率。邹达懿[4]等对客机复材平尾采用有限元方法分析了膜单元与壳单元的区别，并初步验证了复合材料蒙皮的优越性和可行性。门坤发等[5]采用有限元方法分析得出了直升机平尾的详细尺寸。V. B. Gantovnik等[6]研究了改善的遗传算法，优化复合材料层合结构，提高优化效率。

直升机平尾是保证纵向静稳定性的关键部件。针对复合材料平尾优化设计的变量多、计算优化过程复杂与结果准确性低等问题，本文采用将有限元软件PATRAN/NASTRAN在优化平台软件ISIGHT[7]的基础上与遗传算法[8]相结合，再通过C++编程实现设计变量输入与计算结果输出自动读写的方法对复合材料平尾进行优化设计。

1 模型及参数

参考目前国内陆海空三军大量服役的某型直升机的总体尺寸数据，确定了平尾结构形式和尺寸。采用的平面形状为梯形，平尾展长为2.08m，根翼肋弦长为1.103m，梢翼肋弦长0.835m，前缘后掠角为3.5°。平尾由连接梁、前缘腹板、后缘腹板、翼肋以及蒙皮构成，连接梁与斜撑杆采用合金钢，前后缘腹板、翼肋以及蒙皮采用复合材料。具体模型如图1。

将几何模型导入有限元软件PATRAN，分别将蒙皮、腹板与翼肋划分为Shell单元，将连接梁与斜撑杆划分为Beam单元。

本文研究的是直升机平尾在受到设计极限载荷的作用下，复合材料蒙皮、翼肋以及腹板的优化设计。约束条件是合金钢的应力应不超过350MPa，复合材料的应变应不超过3500με，同时复合材料单层应满足蔡-吴强度设计准则，平尾最大位移应不超过60mm，再约束连接梁与斜撑杆和机身连接处两个节点的6个自由度。

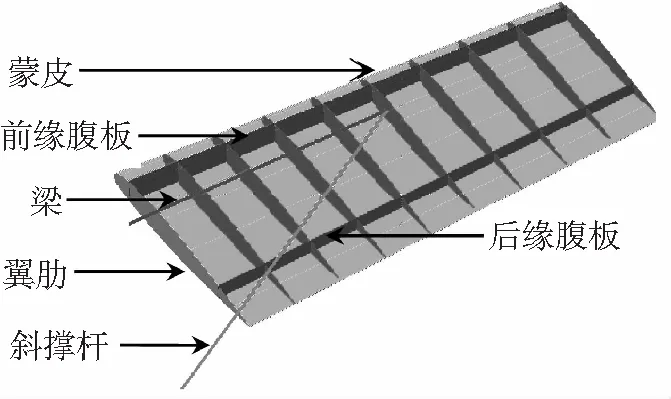
图1 几何模型

根据《军用直升机强度和刚度规范》，平尾计算分析取任意状态载荷与阵风载荷之间较大者。任意状态载荷计算公式如下：

(1)

阵风载荷包括阵风引起的载荷与速度引起的载荷，计算公式分别是式(2)、式(3)：

(2)

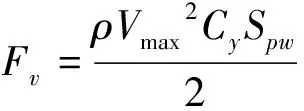
(3)

针对复合材料选材，所应遵循的一般原则和各种要求详见文献[9]。参考目前国内直升机结构采用的复合材料的方式和种类,并结合所面临的各种环境和我国现有的复合材料水平，选择T300/QY8911作为机身蒙皮材料，密度是1.6e-9t/mm3，单层的厚度是0.125mm，其参数如表1，表中的单位是MPa。

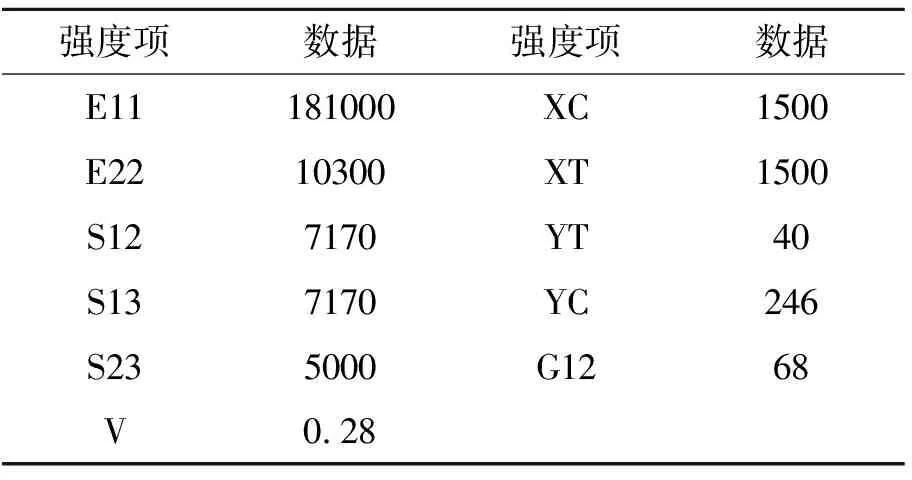
表1 T300/QY8911的材料性能

2 设计变量编码方式

根据复合材料层合结构铺层优化的特点，本文采用了铺层数和铺层角度联合编码的方法[10]。在初始复合材料层合结构中，定义能实现删除单层、改变单层铺层角度这两个操作中至少一个操作的单层为可优化单层。对于可优化单层，用两个整数状态变量来描述这类单层：E变量和A变量。其中E变量表示此单层存在与否，A变量表示该单层的铺层角度。E的取值范围是(0，1)，当为0时说明此单层不存在。A的取值是(1，2，3，4)，定义1为-45°，2为0°，3为 45°，4为 90°。

3 优化数学模型和优化步骤

复合材料层合结构在特定工况下，以质量最小为优化目标，在优化过程中引入模式相关失效准则,本文采用Tsai-Wu准则，要求结构内部任一点的蔡吴数小于1，蔡吴数的计算公式如下：

Hmax=F11σ12+2F12σ1σ2+F22σ22+

F66τ122+F1σ1+F2σ2

(4)

对于刚度约束，本文采用的是限制结构的最大位移量，要求结构的最大位移量小于给定的位移限制参考值，由此可以建立复合材料结构单目标优化设计的数学模型：

Min:W(E,A)

s.t:

(5)

其中，W表示结构的质量，Hmax、Dmax分别表示结构的最大蔡吴数和最大位移值，Dref是给定的最大位移限制值，本文中取60mm，即结构的最大位移限制值是60mm，ai、ei分别代表铺层角度和铺层的有无。

本文采用的是ISIGHT软件自带的NSGA-Ⅱ遗传算法[11]，可以保证优化结果最终收敛到全局最优解。在ISIGHT中设置遗传算法参数，如表2。

表2 ISIGHT中遗传算法参数

图2为复合材料机身优化设计流程图[12]。

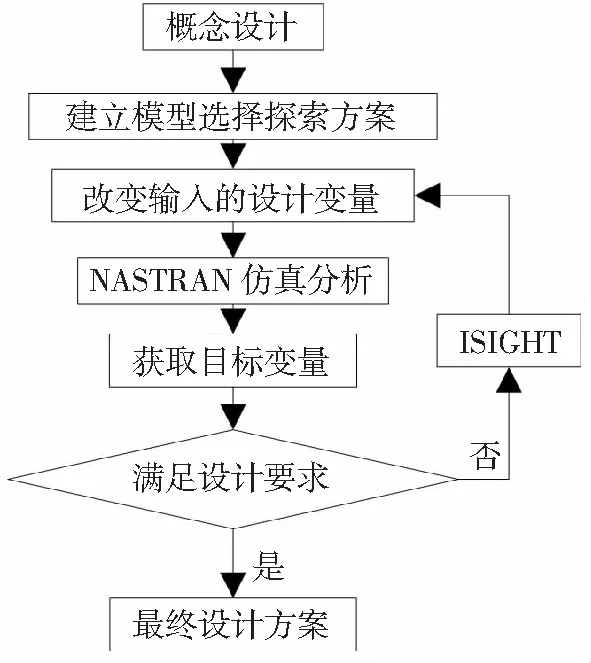
图2 复合材料平尾优化设计流程图

4 优化结果

本文将C++软件编写的读写、查找、计算以及比较等功能的程序与ISIGHT软件的控件模块化，实现相应功能具体如下：首先将读入的初始设计方案提交给优化平台；其次调用NASTRAN解算器，经过计算得到结果文件；再次在结果文件中读取查找应力、应变、最大位移以及质量，同时根据复合材料的应力值进行计算比较得到每一单层的最大蔡吴数；最后自动将结果数据输出。每当计算完成一次后，将自动生成新的设计变量。根据设置的种群大小与种群代数，优化过程将会循环相应的步数，最终得到全局最优解。ISIGHT软件优化模型图如图3。

图3 ISIGHT优化模型图

初始方案为W=(E、A)=((1、1、1、1、1、1、1、1、1、1、1、1、1、1、1、1)(4、3、1、2、4、3、4、1、3、4、1、3、2、4、3、1)) ，复合材料机身采用对称铺层，最大层数为32，质量是37.2kg。通过ISIGHT优化后的优化结果方案是W=((1、0、0、1、1、1、1、1、0、1、0、0、0、1、0、0)(2、3、4、2、4、3、2、1、1、4、2、2、4、1、1、4))。最终层数是16层，厚度是2mm。

由于ISIGHT优化平台的遗传算法种群大小50，种群代数是10，所以结果文件具有500个迭代值，为了更加清晰地分析数据的发展趋势，以下将选择100个迭代值。前200步(前4代)是对全局进行搜索，找出优异子代，一般数据会出现较大的跳变，故选择的100个迭代值将侧重于最后的4代。首先从图5可以看出平尾质量变化是以复合材料每层质量为公差呈现出有规律的几个离散点的跳动，变化曲线如图4所示。

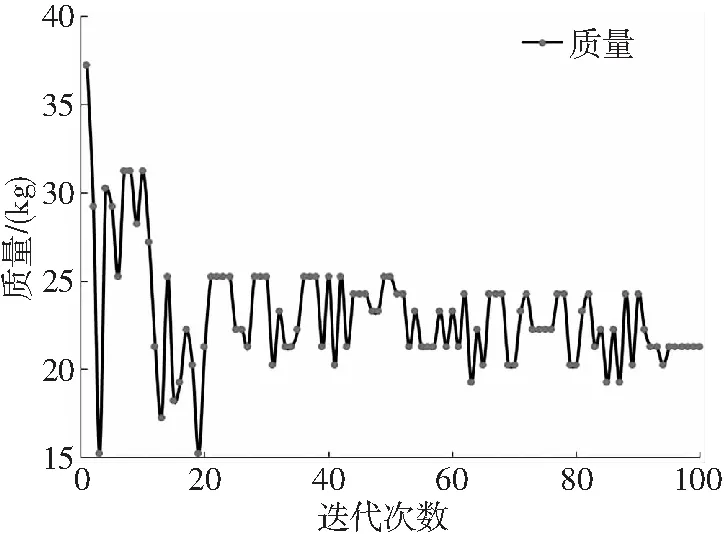
图4 质量迭代图

随着种群个体的不断进化，质量的变化趋势在不断地减小。图中可以看出质量在20步以后开始了小范围的跳变，在90步以后，质量开始收敛，最后的平尾质量是21.33kg。经过优化前后的比较，减少了15.87kg，减少的比例在42.7%左右。在优化过程中，最大位移应当不超过60.00mm，具体的位移变化如图5所示。从图中可以看出，其变化趋势与质量基本一致。最大位移在前20步迭代过程中逐渐减小，之后随着种群范围的缩小，最大位移变化量稳定，最终收敛到57.50mm。

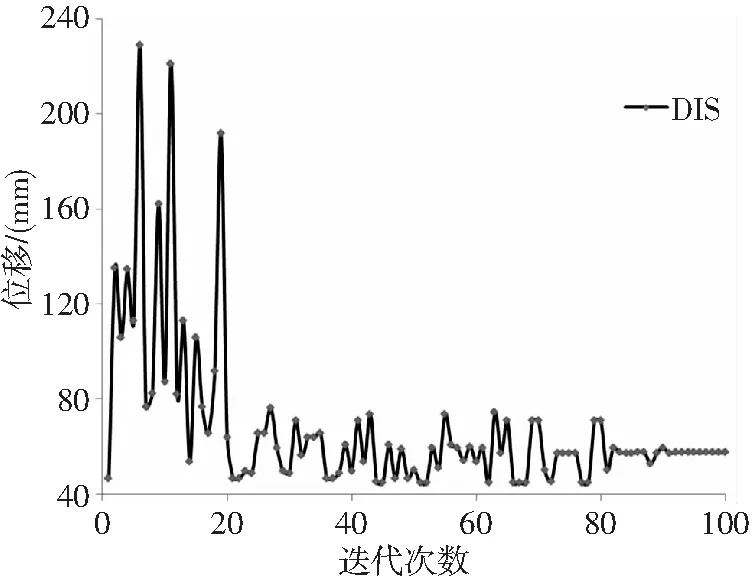
图5 最大位移迭代图

通过约束复合材料每单层的蔡吴数小于1，保证复合材料不出现破坏。表3给出了10组关于铺层数、铺层角度以及最大蔡吴数的数据。

从表3可以看出，铺层角度、铺层数量以及铺层的顺序均对机体结构的强度产生影响。首先铺层数对蔡吴数的影响显而易见；其次1组与5组数据对比发现90°铺层占有的比例高，将降低结构强度；最后4组数据显示±45°铺层数占40%～50%，90°方向铺层占20%，0°方向铺层占30%～40%，有利于提高结构承载效率[12]，同时±45°铺层位于复合材料上下半层中心位置比较合理，±45°铺层彼此先后顺序对强度影响不大。平尾最后的铺层方案是[0/90/45/-45/45/-45/0/0]s。在迭代过程中，最大蔡吴数变化趋势见图6。

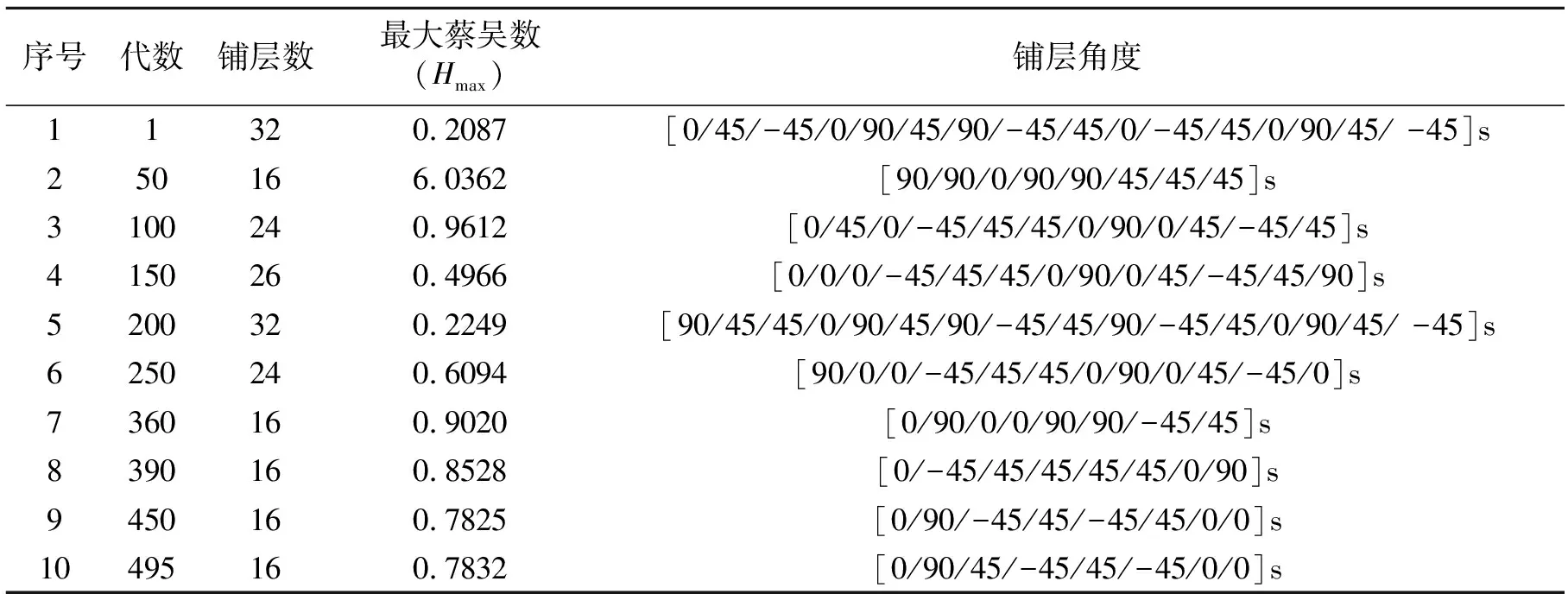
表3 ISIGHT优化中最大蔡吴数、铺层数和铺层的角度的变化

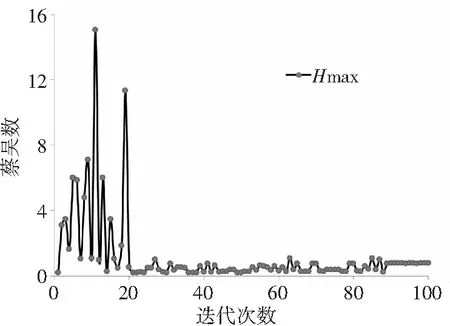
图6 最大蔡吴数迭代图

从图6可以看出最大蔡吴数的变化趋势与质量、最大位移的迭代过程变化相似。

下面将优化前后的复合材料和金属材料平尾结构相对比。其中金属结构的蒙皮、长桁、腹板以及翼肋采用铝合金2A12，连接梁与斜撑杆采用相同的合金钢。根据目前服役的某型直升机尺寸数据确定平尾的蒙皮厚度为1mm，在金属平尾的载荷和约束与复合材料平尾相同的情况下，比较三种状态的结果如表4所示。

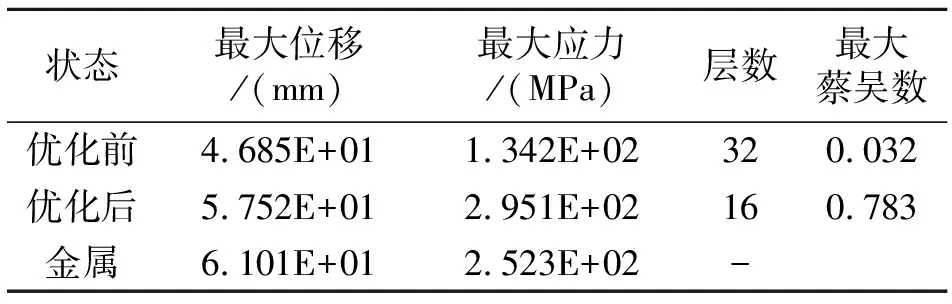
表4 三种状态数据对比

金属材料平尾主要采用铝合金与合金钢，经计算其质量为24.92kg。图7是平尾优化前PATRAN的后处理的位移图。从图中可以看出最大位移是46.8mm。图8是优化后的铺层设计方案位移图，图9是金属机身的位移图，最大的位移分别是57.5mm与61.0mm。

从上图对比可以看出，采用金属材料的平尾相对复合材料优化后的平尾位移大，质量大。复合材料平尾经过优化，减轻了质量，提高了结构强度，应力虽有所上升但最大应力值在结构承载范围以内。

5 总结

经过计算分析得出，此次优化的结果合理可行，符合复合材料平尾设计相关标准和设计准则。在优化过程中，得出了如下结论：

1)采用在ISIGHT优化平台软件上将遗传算法与有限元分析软件PATRAN/NASTRAN相结合的研究方法，能够有效处理复合材料结构优化问题，该研究方法可用于解决工程实际问题。

2)本文研究了某型直升机平尾，得出了最终复合材料厚度是2mm，质量较金属平尾减少3.59kg，为直升机减重优化提供参考。

3)本文中翼肋、蒙皮以及腹板的单元属性均采用同一复合材料，对优化结果产生负面影响。下一步研究工作是对翼肋、蒙皮以及腹板单元属性赋予不同的复合材料属性，克服设计变量翻倍、输出结果繁多以及计算过程复杂等问题。

参考文献：

[1] 肖文萍,等.腐蚀环境因子对树脂基复合材料性能影响研究[J].装备环境工程,2008(12):76.

[2] 刘诗璋.某型直升机复合材料平尾的力学分析[D].南京：南京航空航天大学，硕士论文，2002.

[3] 杨建灵,等.直升机复合材料桨叶铺层三维几何模型建模方法[J].航空学报,2010(1):191-197.

[4] 邹达懿,王鹏飞.复合材料平尾有限元建模方法研究[J].国外电子测量技术,2012,31(7):24-27.

[5] 门坤发,徐海斌,等.某直升机平尾有限元仿真与试验验证[J].计算机辅助工程,2015,24(3):9-12.

[6] Gantovnik V B, Anderson-Cook C M, Gurdal Z, et al. A Genetic Algorithm with Memory for Mixed Discrete-Continuous Design Optimization,[J].Computers and Structures, 2003, 81(20):2003-2009.

[7] 李 亮，孙 秦.基于MSC．Nastran的T型尾翼优化设计研究[J]. 航空计算技术，2010,40(5):9-14.

[8] 晏 飞.复合材料层合结构优化设计的遗传算法[J]. 上海航天，2003(3)：23-25.

[9] 王耀先.复合材料结构设计[M].北京：化学工业出版社，2005.

[10] Kim J S, Kim C G. Optimum Design of Composite Structures with Ply Drop Using Genetic Algorithm and Expert System shell[J]. Composite Structures, 1999(46):171-187.

[11] Fatemi J,Trompet T. Optimization of stiffened panels using a modified genetic algorithm [R].AAIA-98-4973.

[12] Guest J, Smith L. Topology optimization of continuum structures using HPM encoded genetic algorithms[J] .Structural Dynamics，2008,10,2514/6,2008-1709.