基于多线耦合的互连串扰延时模型

续朋 潘中良

摘 要： 隨着半导体的生产技术进入纳米级，大规模集成电路（VLSI）的集成度不断被提高。由于互连线之间的间距被迅速缩少，故互连线的耦合串扰效应已经严重影响了VLSI的整体性能。首先，提出一个三线耦合的等效电路模型，该模型结合了耦合电容和互感电感;其次，在该等效电路模型的基础上，通过运用解耦技术和ABCD参数矩阵的方法构造一个精确计算三线耦合的互连串扰延时模型;此外，还对比和分析了双线耦合和三线耦合的延时性能;最后，研究互连间距对串扰延时的影响。实验数据结果显示，采用非并行布线规则和增大互连间距均能有效降低串扰延时，提出的多根互连线的串扰延时模型和Spice仿真结果保持了高度的一致性。

关键词： 大规模集成电路; 互连耦合; 串扰延时; 解耦技术; ABCD参数矩阵; 互连间距

中图分类号： TN47?34 文献标识码： A 文章编号： 1004?373X（2018）12?0019?05

Abstract： With the semiconductor production technology going into the nanoscale level， the integration level of the very large scale integrated circuit （VLSI） is constantly improved. The coupling crosstalk effect of interconnected lines has seriously affected the overall performance of the VLSI due to the rapid reduction of the spacing between interconnected lines. Therefore， an equivalent circuit model based on three?line coupling is proposed， in which coupling capacitance and mutual inductance are combined. On the basis of the equivalent circuit model， an interconnection crosstalk delay model for accurate calculation of three?line coupling was constructed by adopting the decoupling technique and ABCD parameter matrix approach. The time delay performances of two?line coupling and three?line coupling were compared and analyzed. The influence of interconnection spacing on crosstalk delay was studied. The results from experimental data show that both applying the non?parallel routing rule and increasing the interconnection spacing can effectively reduce the crosstalk delay. The proposed crosstalk delay model for multiple interconnected lines maintains high consistency with the SPICE simulation results.

Keywords： VLSI; interconnection coupling; crosstalk delay; decoupling technique; ABCD parameter matrix; interconnection spacing

随着硅互补金属氧化物半导体（CMOS）的生产工艺不断提高，集成电路的最小特征尺寸不断缩小，因此大规模集成电路（VLSI）的互连总长度和复杂度急剧增加。半导体集成电路的生产工艺已进入了纳米级，故互连线之间的间距被迅速缩小。随之而来，互连线之间产生了耦合电容和互感电感，而纳米级互连线的耦合电容值甚至是其对地电容的几倍，故互连线之间形成的耦合串扰不能再被忽略[1?4]。未来随着集成电路的最小特征尺寸继续缩小，由耦合串扰形成的互连延时必定会成为影响VLSI总体性能的重要因素，因此如何精确计算和降低互连线的串扰延时是本文的工作重点。

1 三根互连线的耦合等效电路

根据伯克利科技预测模型（BPTM）[5]，一个典型的三线并行互连结构如图1所示。 图中：t和w分别是互连线的高和宽;s表示互连间距;h是互连线底端到接地端之间的介质层厚度。

2 串扰延时模型

通常互连串扰是由并行的互连线间存在耦合电容和互感电感形成的，如图2所示，[C12]，[C23] 均是耦合电容，[M12]，[M23] 和[M13]均是互感电感。由于本文研究的模型是多线耦合，故将上述的耦合电容和互感电感分别表示为[Cij]和[Mij]（i，j=1，2，3）。互连串扰可被分成动态串扰和功能串扰。处在功能串扰时，比如图2中的线2和线3均没有输入信号，而线1输入一个阶跃信号，此时线2和线3的输出信号即是功能串扰，功能串扰即是输出噪声。而处在动态串扰下，三根互连线同时输入不同的逻辑跳变方向的阶跃信号，其跳变方向可以从逻辑状态0跳变至1，也可从1跳变到0。因此动态串扰可分成同相串扰和反相串扰，例如线1和线2的输入信号均同时从逻辑0跳变到1，此时这双线间形成了同相串扰;如果线1和线2其中一根线的输入信号从逻辑0跳变到1，另外一条线同时从逻辑1跳变到0， 则此双线间形成了反相串扰。

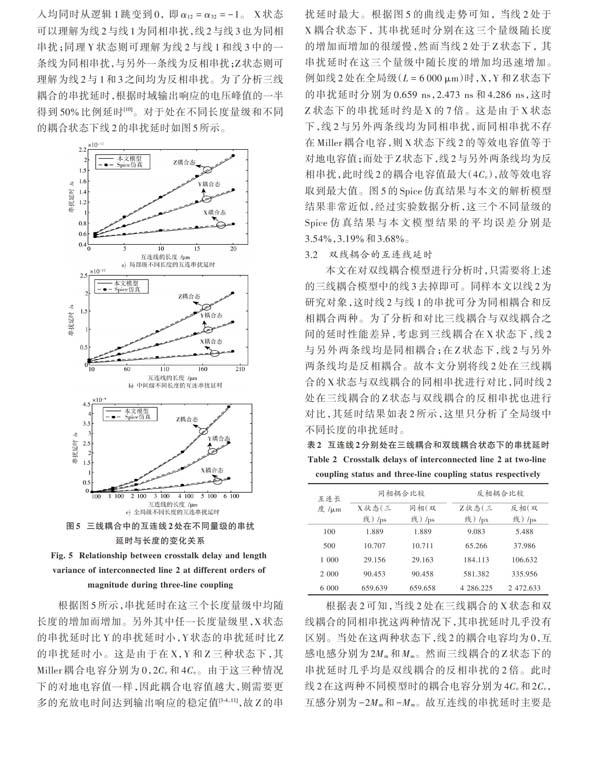
本文定義了线2与线1和线3的三种耦合状态，X耦合状态：线2与线1和线3的输入电压信号均同时从逻辑0跳变到1，即[α12=α32=1];Y耦合状态：线2的输入电压信号从逻辑0跳变到1，线1和线3其中一根线的输入从逻辑1跳变到0，而另外一根线的输入从逻辑0跳变到1，即[α12=1，α32=-1] 或[α12=-1，α32=1];Z耦合状态：线2的输入从逻辑0跳变到线1，而线1和线3的输入均同时从逻辑1跳变到0， 即[α12=α32=-1]。 X状态可以理解为线2与线1为同相串扰，线2与线3也为同相串扰;同理Y状态则可理解为线2与线1和线3中的一条线为同相串扰，与另外一条线为反相串扰;Z状态则可理解为线2与1和3之间均为反相串扰。为了分析三线耦合的串扰延时，根据时域输出响应的电压峰值的一半得到50%比例延时[10]。对于处在不同长度量级和不同的耦合状态下线2的串扰延时如图5所示。

根据图5所示，串扰延时在这三个长度量级中均随长度的增加而增加。另外其中任一长度量级里，X状态的串扰延时比Y的串扰延时小，Y状态的串扰延时比Z的串扰延时小。这是由于在X，Y和Z三种状态下，其 Miller耦合电容分别为0，[2Cc]和[4Cc]。由于这三种情况下的对地电容值一样，因此耦合电容值越大，则需要更多的充放电时间达到输出响应的稳定值[3?4，11]，故Z的串扰延时最大。根据图5的曲线走势可知， 当线2处于X耦合状态下， 其串扰延时分别在这三个量级随长度的增加而增加的很缓慢，然而当线2处于Z状态下， 其串扰延时在这三个量级中随长度的增加均迅速增加。例如线2处在全局级（[L=6 000 μm]）时，X，Y和Z状态下的串扰延时分别为0.659 ns，2.473 ns和4.286 ns，这时Z状态下的串扰延时约是X的7倍。这是由于X状态下，线2与另外两条线均为同相串扰，而同相串扰不存在Miller耦合电容，则X状态下线2的等效电容值等于对地电容值;而处于Z状态下，线2与另外两条线均为反相串扰，此时线2的耦合电容值最大（[4Cc]），故等效电容取到最大值。图5的Spice仿真结果与本文的解析模型结果非常近似，经过实验数据分析，这三个不同量级的Spice仿真结果与本文模型结果的平均误差分别是3.54%，3.19%和3.68%。

3.2 双线耦合的互连线延时

本文在对双线耦合模型进行分析时，只需要将上述的三线耦合模型中的线3去掉即可。同样本文以线2为研究对象，这时线2与线1的串扰可分为同相耦合和反相耦合两种。为了分析和对比三线耦合与双线耦合之间的延时性能差异，考虑到三线耦合在X状态下，线2与另外两条线均是同相耦合;在Z状态下，线2与另外两条线均是反相耦合。故本文分别将线2处在三线耦合的X状态与双线耦合的同相串扰进行对比，同时线2处在三线耦合的Z状态与双线耦合的反相串扰也进行对比，其延时结果如表2所示，这里只分析了全局级中不同长度的串扰延时。

根据表2可知，当线2处在三线耦合的X状态和双线耦合的同相串扰这两种情况下，其串扰延时几乎没有区别。当处在这两种状态下，线2的耦合电容均为0，互感电感分别为[2Mm]和[Mm]。然而三线耦合的Z状态下的串扰延时几乎均是双线耦合的反相串扰的2倍。此时线2在这两种不同模型时的耦合电容分别为[4Cc]和[2Cc]，互感分别为[-2Mm]和[-Mm]。故互连线的串扰延时主要是由耦合电容决定，互感电感对串扰延时的作用并不突出。另外由表2的数据可知，当处于反相串扰时，三线耦合的延时约是双线耦合的2倍，故采取非并行布线规则可有效地降低互连反相串扰延时，即减少并行互连线的根数或减少并行长度。

3.3 互连间距对串扰延时的影响

本文以三线耦合模型为分析对象，具体分析了互连间距对串扰延时的影响。对于处在不同量级和不同的耦合状态的线2随互连间距变化的串扰延时见图6。

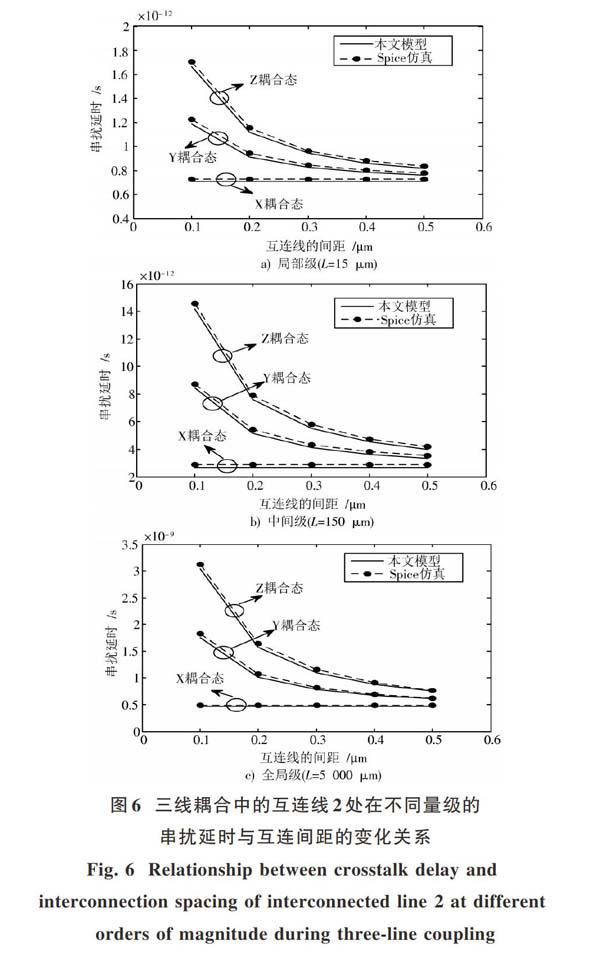
由图6可知，对于三线耦合的Y和Z两个耦合状态，线2的串扰延时在这三个不同的量级中均随互连间距的增加而减少;而X状态下，线2的串扰延时不随互连间距的增加而改变。这是由于X状态下不存在耦合电容，而在Y和Z两种状态下，随着互连间距的增加，线2的耦合电容迅速减小。另外当线2处于延时最大的耦合状态（Z状态），增大互连间距能大幅降低延时。例如线2处于全局级时（[L=5 000 μm]），互连间距为[0.1 μm]时的串扰延时大约是间距为[0.5 μm]时的4倍。故增大互连间距能大幅降低由耦合电容形成的串扰延时。图6的Spice仿真结果与本文的解析模型的结果非常相近，经过实验数据分析，其最大误差在这三个不同的长度量级中是3.46%。基于以上实验结果可知，处于三线模型的互连线2，当其与另外两条线均处于反相耦合时（Z状态）的串扰延时最大，与另外两条线均处于同相耦合时（X状态）的串扰延时最小。相比较双线耦合，三线耦合的最大反相延时（Z状态）比双线耦合的反相延时大，因此采用非并行布线规则能有效降低互连串扰延时。另外增大互连间距也可大幅降低互连串扰延时。

4 结 论

本文提出一个三线耦合的等效电路模型，该模型同时考虑了耦合电容和互感的影响。通过运用解耦技术和ABCD参数矩阵的方法构造一个精确计算三线耦合的串扰延时模型。通过运用该解析模型发现，处于中间的互连线与另外两条线均是反相串扰时的延时最大。同时本文将该三线耦合模型与双线耦合进行延时对比，双线耦合的反相延时要小于三线耦合的反相延时，故采取非并行布线规则可有效地降低串扰延时。最后本文研究了互连间距对三线耦合的串扰延时的影响，得出增大互连间距可大幅降低由耦合电容形成的串扰延时。本文提出的解析模型与Spice仿真软件结果之间的误差均保持在5%以内。因此本文对着重考虑延时性能的VLSI半导体芯片的互连时钟网络和互连路由结构的设计提供了有意义的参考。

注：本文通讯作者为潘中良。

参考文献

[1] Semiconductor Industry Association. 2011 International technology roadmap for semiconductors [M]. Berlin： Springer， 2011.

[2] SHARMA D K， KAUSHIK B K， SHARMA R K. Signal integrity and propagation delay analysis using FDTD technique for VLSI interconnects [J]. Journal of computational electronics， 2014， 13（1）： 300?306.

[3] AGARWAL Y， CHANDEL R. Crosstalk analysis of current?mode signaling?coupled RLC interconnects using FDTD technique [J]. IETE technical review， 2016， 33（2）： 148?159.

[4] KUMAR V R， KAUSHIK B K， PATNAIK A. An accurate FDTD model for crosstalk analysis of CMOS?Gate?Driven coupled RLC interconnects [J]. IEEE transactions on electromagnetic compatibility， 2014， 56（5）： 1185?1193.

[5] Nanoscale Integration and Modeling Group. Predictive technology model [EB/OL]. [2011?06?01]. http：//ptm.asu.edu/.

[6] TUUNA S， NIGUSSIE E， ISOAHO J， et al. Modeling of energy dissipation in RLC current?mode signaling [J]. IEEE transactions on very large scale integration systems， 2012， 20（6）： 1146?1151.

[7] MAJUMDER M K， KUKKAM N R， KAUSHIK B K. Frequency response and bandwidth analysis of multi?layer grapheme nanoribbon and multi?walled carbon nanotube interconnects [J]. IET micro & nano letters， 2014， 9（9）： 557?560.

[8] SAHOO M， RAHAMAN H. Modeling of crosstalk induced effects in copper?based nanointerconnects： an ABCD parameter matrix?based approach [J]. Journal of circuits， systems & computers， 2015， 24（2）： 361?382.

[9] ZHAO W， WANG G， HU J， et al. Performance and stability analysis of monolayer single?walled carbon nanotube interco?

nnects [J]. International journal of numerical modelling： electronic networks， devices and fields， 2015， 28（4）： 456?464.

[10] LU Q， ZHU Z， YANG Y， et al. Analysis of propagation delay and repeater insertion in single?walled carbon nanotube bundle interconnects [J]. Microelectronics journal， 2016， 54（C）： 85?92.

[11] KUMAR V R， KAUSHIK B K， PATNAIK A. Crosstalk noise modeling of multiwall carbon nanotube （MWCNT） interconnects using finite?difference time?domain （FDTD） technique [J]. Microelectronics reliability， 2015， 55（1）： 155?163.