竖向荷载下空心楼盖板柱节点试验研究与计算分析
党隆基 庞 瑞 梁书亭 朱筱俊
(1东南大学土木工程学院, 南京 211189)(2河南工业大学土木建筑学院, 郑州 450001)(3东南大学建筑设计研究院有限公司, 南京 210096)
空心楼盖板柱结构体系是在传统板柱结构体系中采用空心楼盖的一种组合结构体系.该结构既具有空心楼盖自重较轻、隔音效果优良和节能效果显著等优势[1],又兼顾了板柱结构大柱网、大开间、降低层高和空间布置灵活等特点,可有效降低能源消耗,实现节能减排和保护环境的效果.由于节点是板柱结构的薄弱部位,空心楼盖板柱结构体系能否有效推广主要取决于节点的抗冲切性能.
目前,板柱节点的研究大多集中于实心板柱结构,多种抗冲切元件已被应用于板柱结构中,其中箍筋、弯起钢筋研究较早,并已形成较为成熟的设计方法[2].国内外学者致力于抗冲切元件的开发和应用研究,主要包括U形箍筋[3]、抗剪栓钉[4]、抗剪螺栓[5]、拉筋[6]、剪切带[7]、钢筋桁架[8]和型钢剪力架[9]等,研究结果表明,不同抗冲切元件均可等同于抗剪钢筋参与节点抗剪,提高了节点承载力和抑制裂缝开展,延缓了节点的脆性破坏.针对空心板柱结构,龚启宏等[10-11]进行了无抗冲切元件空心楼盖板柱节点的抗冲切性能试验,结果表明,竖向荷载作用下空心楼盖板柱节点破坏形态与实心板的冲切破坏类似,并提出了节点受冲切承载力计算方法.然而,关于配置抗冲切元件的空心楼盖板柱节点试验研究则鲜有报道,此类节点的受力机理和破坏形态还不够明确,相关节点极限承载力计算方法也并未有所涉及.
本文在空心板柱结构中节点试验研究的基础上,以提高节点极限承载力和避免节点发生冲切破坏为目标,在节点局部实心和布置暗梁的前提下,研究了抗冲切元件和板厚对空心楼盖板柱节点受力性能的影响.在不明显提高结构造价的前提下,分析了合理可靠的节点构造措施,提出了节点的极限承载力计算方法,为空心板柱结构的推广应用提供参考.
1 试验
1.1 试件设计

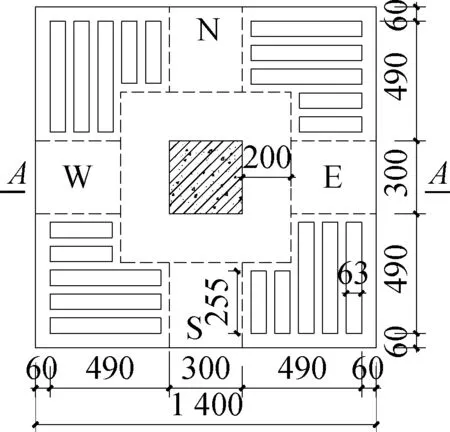
(a) h=120 mm

(b) h=140 mm图1 空心楼盖平面布置图(单位:mm)

图2 无冲切元件节点构造图(单位:mm)

(a) 弯起钢筋

(b) 型钢剪力架图3 抗冲切元件照片
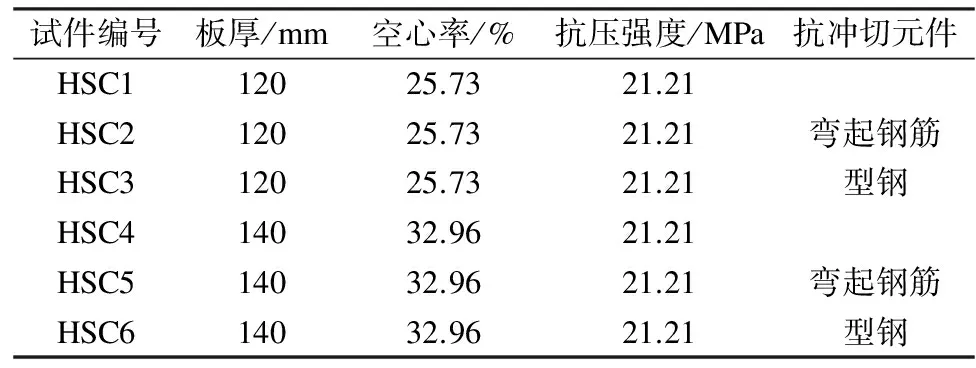
表1 试件主要参数
1.2 试验加载与测试方案
试件通过液压伺服千斤顶对柱顶施加竖向荷载.为更好地模拟实际工程中四边简支板的受力状态,采用4个外径为60 mm的圆钢作为支座.为避免圆钢滑移较大,将圆钢和π形等边角钢焊接,并通过长圆孔固定于支撑钢壿(见图4).将矩形钢板通过膨胀螺丝固定于板底表面以防止试验板在支座处发生剪切破坏,其中钢板厚度为14 mm,宽度为120 mm,圆钢中心距板边距离为60 mm.

图4 试验加载装置照片
所有试件均采用逐级加载的方式.首先,对试件进行预加载,待仪器仪表正常工作后正式加载.每级持荷时间为8 min,期间描绘记录试件的裂缝形态和发展趋势.试验测试的主要内容包括试件各阶段的荷载值、下柱中心挠度、四角翘曲位移、钢筋应变、抗冲切元件应变等.
2 试验结果
2.1 荷载-位移曲线
试件荷载-挠度曲线见图5.由图可知,6个试件的荷载-位移曲线整体相似.荷载达到峰值后并未快速下降,位移则保持缓慢增长的趋势,试件表现出良好的强度和塑性变形能力.
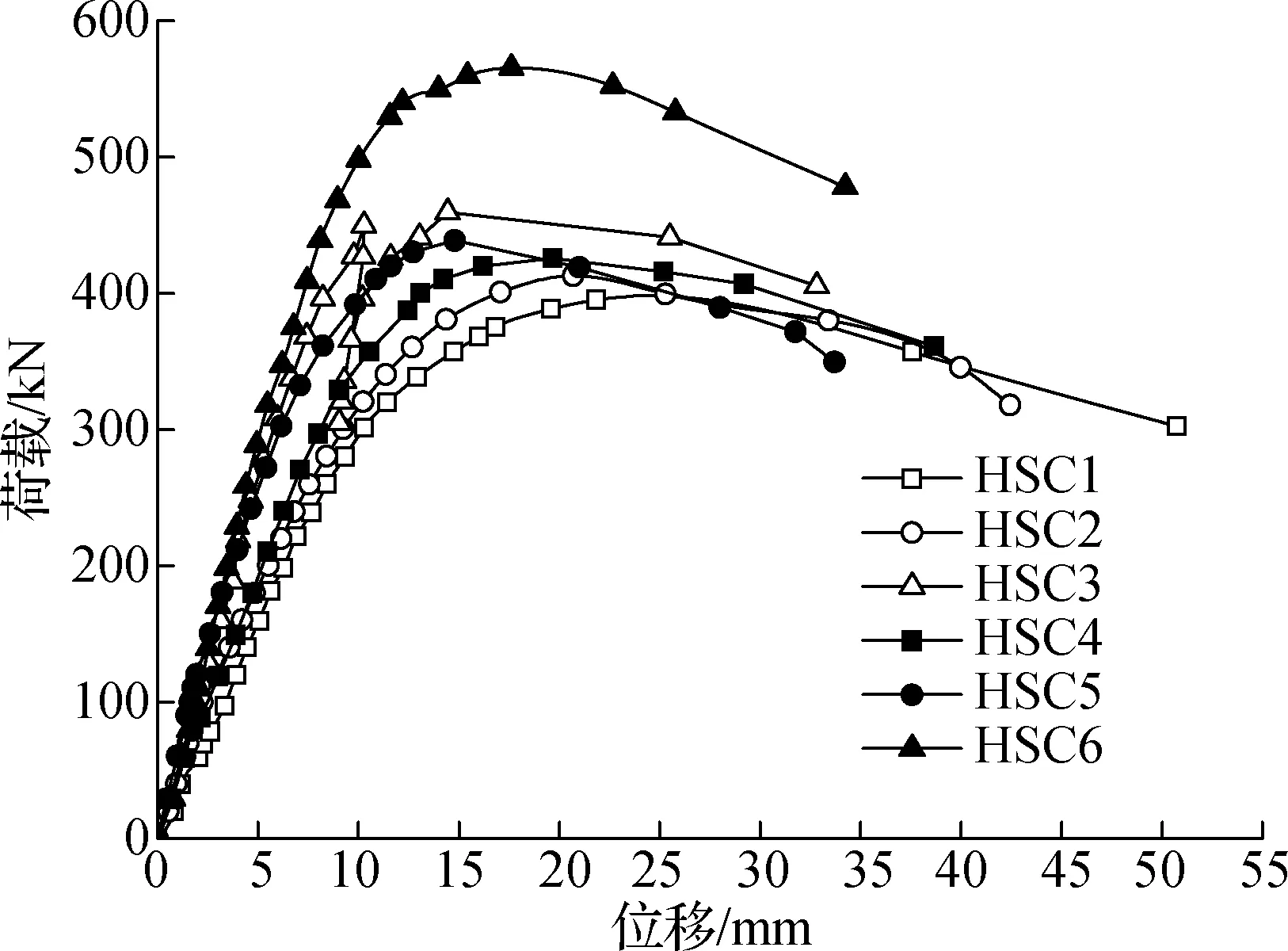
图5 试件荷载-挠度曲线
加载过程中,试件HSC3在型钢焊接部位断裂,导致极限承载力偏小.当板厚由120 mm增加至140 mm时,试件HSC4,HSC5,HSC6的极限承载力分别提高了7.85%,6.04%,23.48%.当板厚相同时,试件HSC2和试件HSC5的极限承载力分别较基本试件提高了4.81%和3.05%,试件HSC3和试件HSC6的极限承载力分别较基本试件提高了16.46%和33.33%.
由上述分析可知,增加板厚和配置抗冲切元件均可提高板柱节点的极限承载力和刚度.与弯起钢筋相比,型钢剪力架对板柱节点极限承载力的提高效果更好.在节点设计时,与增加板厚相比,可优先选择在节点核心区配置型钢剪力架.
2.2 裂缝发展
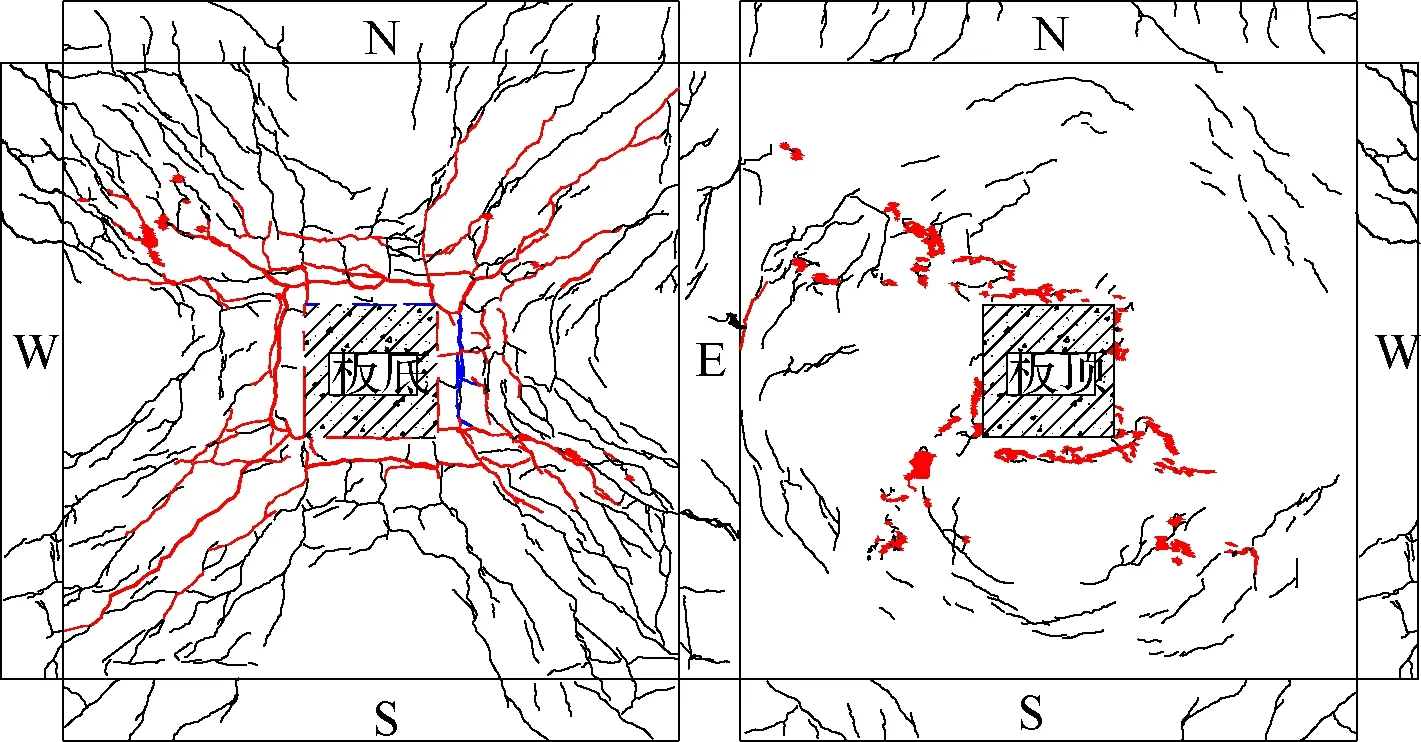
加载至开裂荷载时,板底柱边首先出现裂缝.随着荷载的增加,裂缝逐渐向四角斜向扩展,与板边大体呈45°夹角,同时距离柱边约50 mm处开始出现细微横向裂缝.随着试验的继续进行,试件板侧边开始出现细微斜裂缝,以柱边为中心向板边辐射的裂缝明显增多,柱边附近形成一条环向裂缝,在与板边呈45°夹角的裂缝区形成数条缝宽不断加大的斜向裂缝,变形集中.临近极限荷载时,板底已经密布裂缝,裂缝主要集中在沿对角线向两边发展的区域,呈现出饱满的X形,板底主裂缝由柱边环向裂缝和对角斜裂缝组成,并将试件分割成不同的条状区域.由于型钢剪力架显著的抗剪作用,试件HSC3和HSC6距柱边距离约275 mm处形成了另一条环向主裂缝.达到极限承载力后继续加载,荷载缓慢下降,位移持续增长,持荷约35 min后,荷载下降到极限承载力的85%,宣告试件破坏,此时试件仍表现出良好的挠曲变形能力,节点具有冲切破坏和弯曲破坏的双重破坏模式,但以弯曲破坏为主.试件HSC4,HSC5,HSC6的裂缝示意图见图6.图中,红色表示主裂缝,蓝色表示初始裂缝.
2.3 应变分析
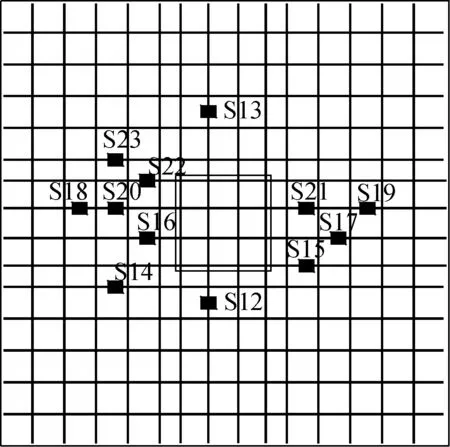
根据板柱节点在竖向荷载作用下的受力机理,在与冲切椎体线相交的钢筋(抗冲切元件)处布置应变片.应变片位置距板中轴线的距离为(150+h0)mm,其中h0为试验板的有效厚度.对于弯起钢筋,选择在弯起段中心部位布置应变片.应变测点分布图见图7.
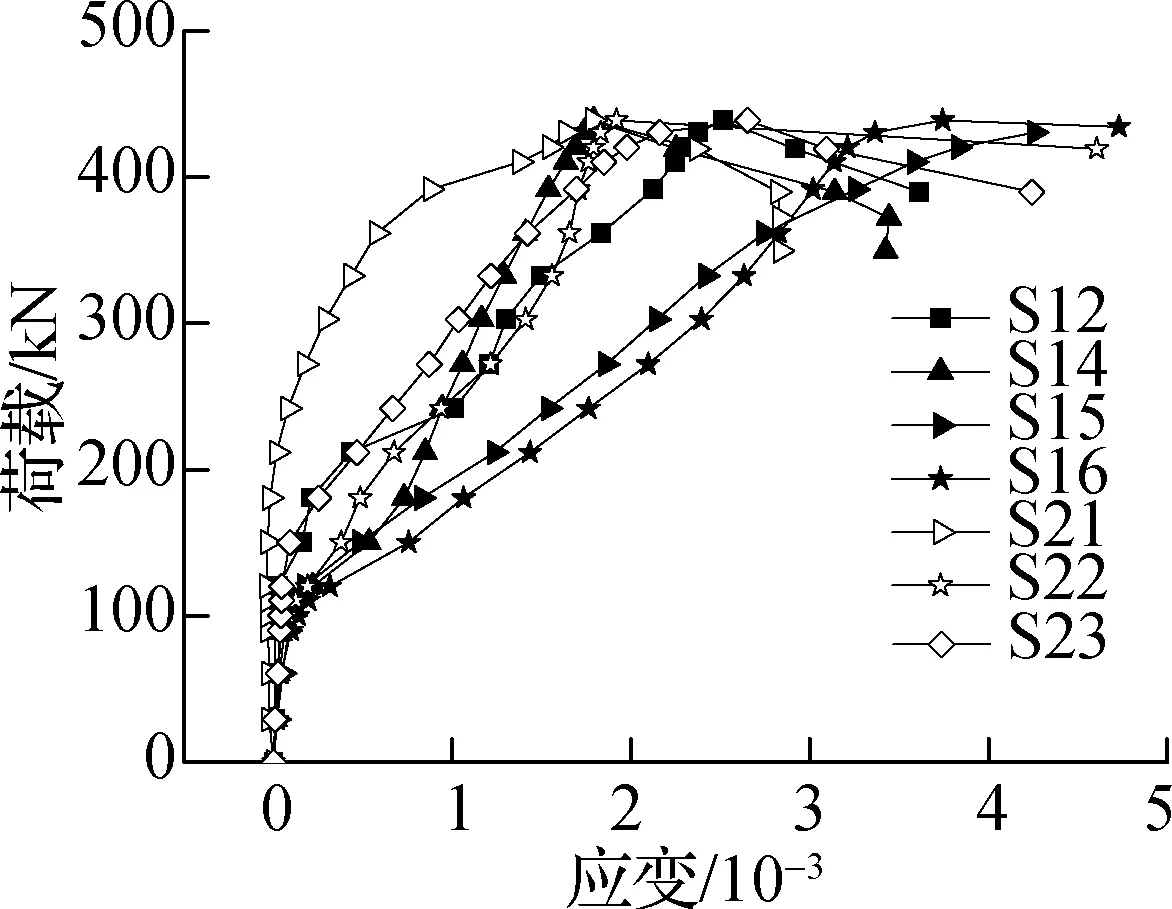
以试件HSC4,HSC5,HSC6为例进行分析,荷载-应变曲线图见图8.由图可知,所有测点的荷载-应变曲线在开裂荷载处均出现明显转角,开裂后钢筋应变增长速率明显增大,此后保持平稳增长.由图8(a)可知,试件HSC4板底柱边环向主裂缝范围内钢筋测点S12,S15,S16,S21和S22均超过钢筋屈服应变值2.67510-3;若以对角斜向主裂缝范围内应变测点作为研究对象,测点S14,S15,S22和S23均达到屈服应变.由图8(b)和(c)可知,在竖向荷载作用下,抗冲切元件均较好地参与节点抗剪,试件HSC5弯起钢筋测点应变值均超过屈服应变值2.67510-3,试件HSC6型钢剪力架下翼缘测点应变值超过屈服应变值1.48510-3.
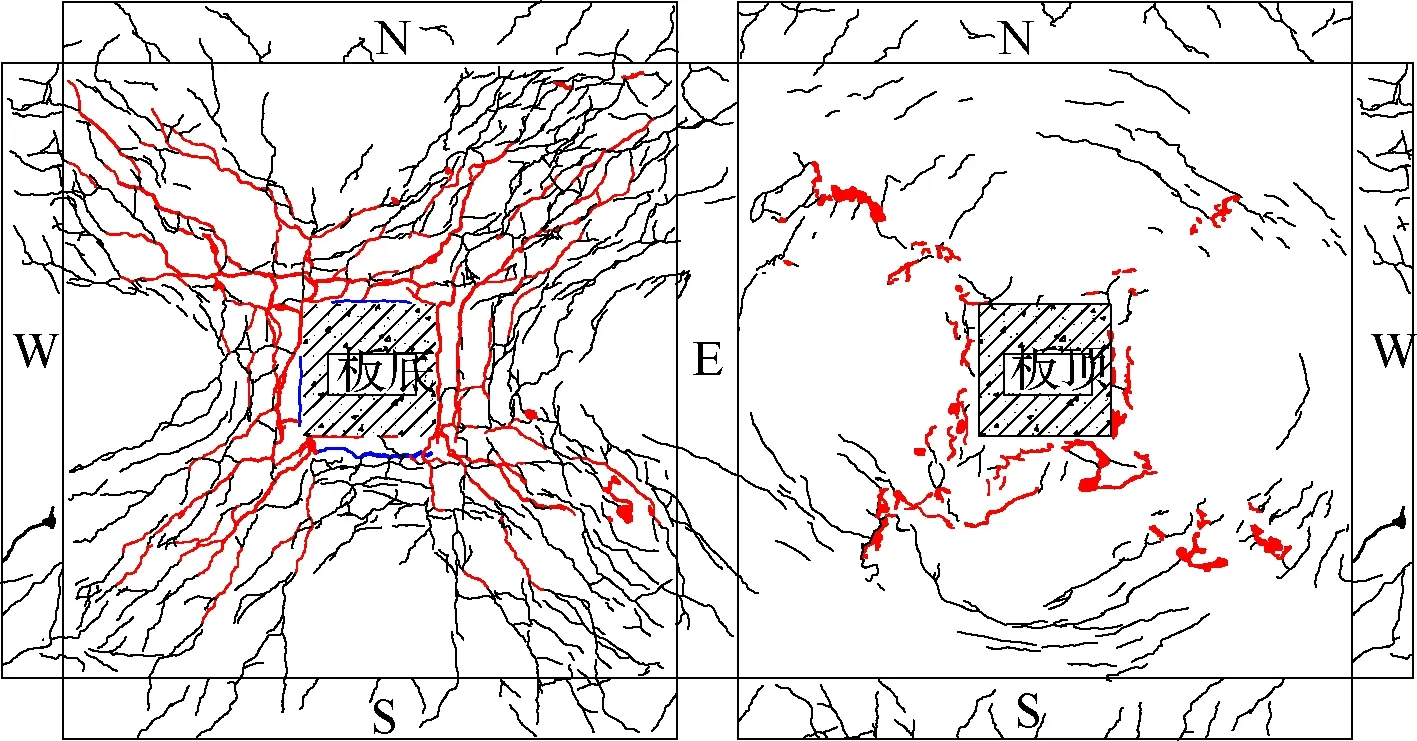
(a) 试件HSC4
(b) 试件HSC5
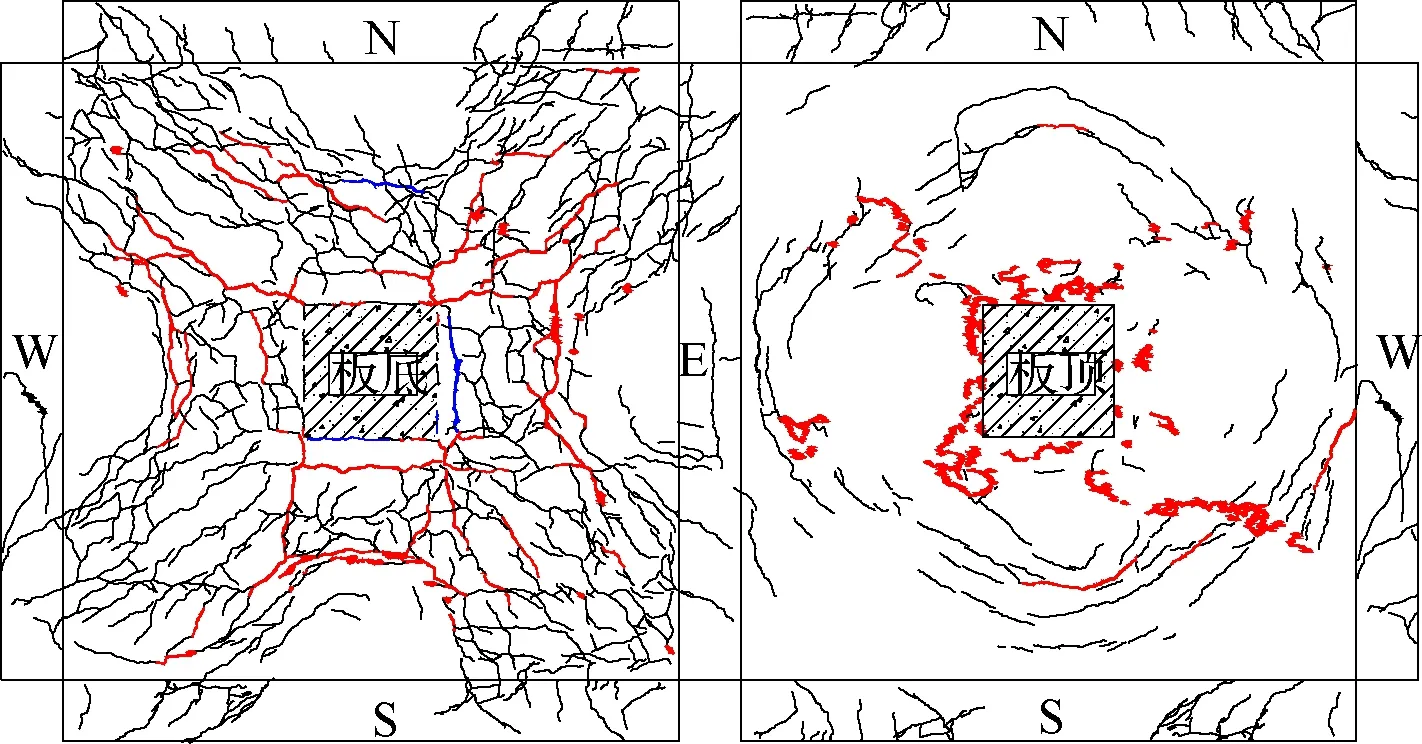
(c) 试件HSC6图6 裂缝分布示意图
(a) 板底钢筋

(b) 弯起钢筋

(c) 型钢下翼缘图7 应变测点分布图
(a) 板底钢筋(HSC4)
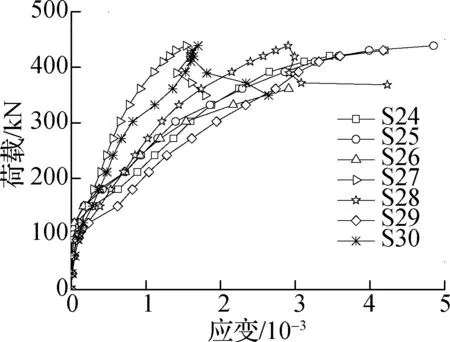
(b) 弯起钢筋(HSC5)
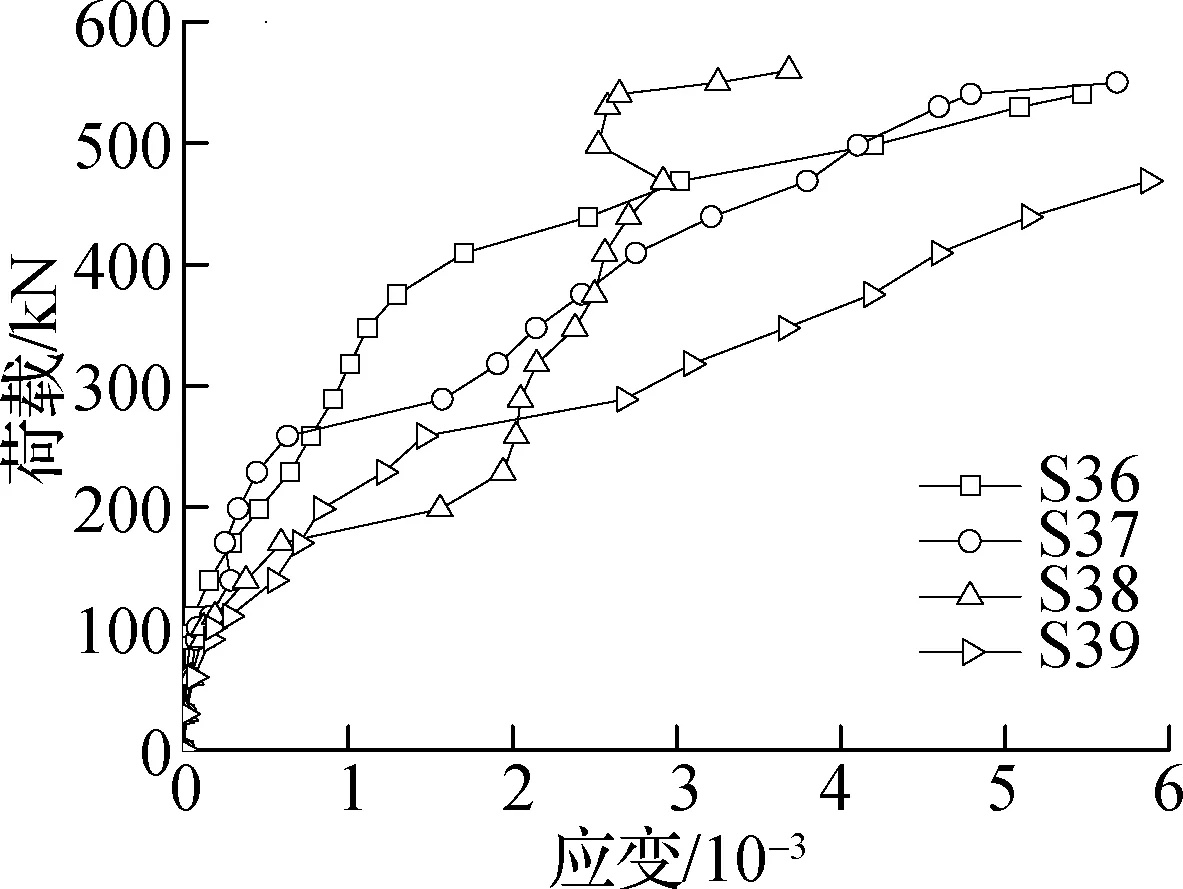
(c) 型钢下翼缘(HSC6)图8 荷载-应变曲线
3 节点的极限承载力计算方法
3.1 屈服线模式
屈服线理论[12]是一种上限分析方法,主要适用于弯曲破坏的研究分析.屈服线理论在计算板弯曲破坏极限承载力时,基于以下2个假定:① 弯曲破坏先于冲切破坏发生;② 与屈服线相交的钢筋均已受拉屈服.马云昌等[13]基于屈服线理论提出了板柱节点在竖向剪力和不平衡弯矩共同作用下的承载力计算公式,且计算值与试验值吻合较好.然而,该研究结果仅适用于无抗冲切元件的实心板柱节点.因此,有必要建立考虑楼板空心和抗冲切元件的板柱节点极限承载力计算方法.
根据图6中试验板的裂缝示意图,得到试验板发生弯曲破坏的假定屈服线模式(见图9).图中,r=0.5(l0-c)为扇形块半径;c为柱边长;l0为板有效支撑长度;δ为扇形中心向下的位移;φ为扇形的弧度.该屈服线模式由以柱角为圆心的4个扇形以及扇形之间的4个矩形组成.在局部荷载作用下,正屈服线以荷载作用点(柱角)直线形放射出去,直至与曲线形的负屈服线相交为止,表现为圆扇形屈服线模式.
由文献[14]可知,根据虚功原理,局部荷载作用下无梁平板的集中荷载为
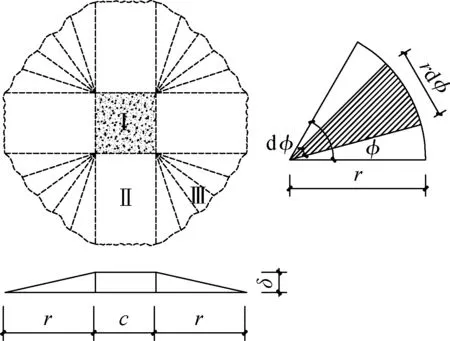
图9 屈服线模式示意图
(1)
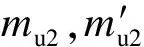
将c=300 mm,l0=1 280 mm代入式(1)可得
(2)
实际结构中,破坏机构屈服线上的钢筋不一定全部达到屈服强度,因此式(2)右侧需要乘以折减系数0.87[13],即
(3)
3.2 极限抵抗矩的计算
3.2.1 楼盖实心部分

(4)
对于配置抗冲切元件实心板柱节点,有
(5a)
(5b)
式中,α1为混凝土受压区等效矩形应力图形系数;fc为混凝土轴心抗压强度设计值;b为截面宽度;x为混凝土受压区高度;fy为受拉钢筋强度设计值;As为单位宽度的受拉钢筋截面面积;Ap为单位宽度的抗冲切元件截面面积.
3.2.2 楼盖空心部分
对于预埋空心管,假定截面惯性矩和截面积均相等,计算模型可简化为I形截面[11].为便于计算,对板柱节点空心区域进行如下假定:
式中,bf为翼缘宽度;Asf,Apf分别纵筋和抗冲切元件截面积.

(a) I形截面

(b) 截面等效应力图图10 I形截面承载力计算简图
进行正截面计算时,不考虑受压区钢材的抗弯作用,可得
(6)
(7)
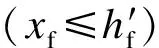
对于第1类I形截面,当混凝土受压区高度在上翼缘内时,根据静力平衡条件可得
α1fcbwxf=fyAsf+fyApf
(8)
(9)

对于第2类I形截面中无抗冲切元件空心板柱节点,有
(10)
对于第2类I形截面中配置抗冲切元件空心板柱节点,有
(11a)
(11b)
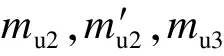
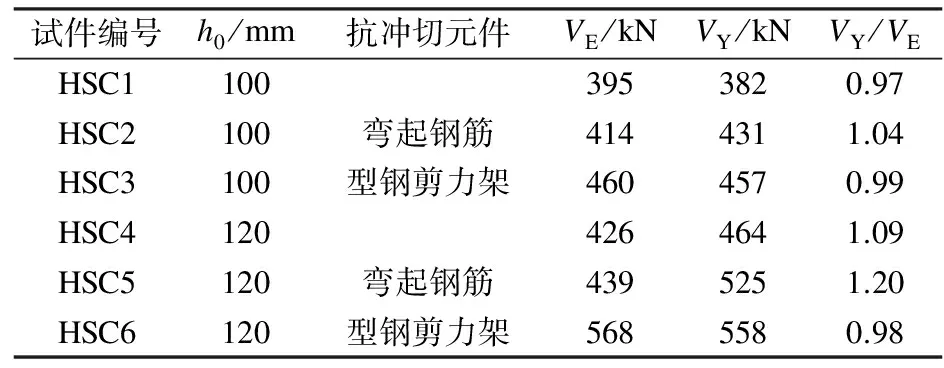
表2 计算值与试验值对比
注:VE为试验值;VY为按屈服线理论得到的计算值.
4 结论
1) 空心楼盖板柱节点破坏后仍具有较好的塑性变形能力.节点具有冲切破坏和弯曲破坏的双重破坏模式,以弯曲破坏为主.
2) 节点的初始裂缝出现在板底柱边;板底主裂缝由柱边环向裂缝和对角斜裂缝组成,其中型钢剪力架具有2条环向主裂缝.
3) 增加板厚和配置抗冲切元件均可提高节点的极限承载力和刚度.与增加板厚和弯起钢筋相比,型钢剪力架对节点极限承载力的提高效果更为明显.在节点设计时,可优先选择配置型钢剪力架参与节点抗剪.
4) 本文提出的节点的极限承载力计算方法综合考虑了抗冲切元件、楼板配筋率和空心率的影响,计算值与试验值吻合较好.
参考文献(References)
[1] Araujo C A M, Loriggio D D, Da Camara J M M N. Anchorage failure and shear design of hollow-core slabs[J].StructuralConcrete, 2011,12(2): 109-119. DOI:10.1002/suco.201000024.
[2] 中华人民共和国住房和城乡建设部. GB 50010—2010混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2015.
[3] 金玉, 易伟建, 胡岚, 等. 配置抗冲切键的钢筋混凝土板柱节点性能试验研究[J]. 工业建筑, 2017, 47(4): 60-64,110. DOI: 10.13204/j.gyjz201704014.
Jin Yu, Yi Weijian, Hu Lan, et al. Experimental study on performance of reinforced concrete slab-column connection with punching shear keys[J].IndustrialConstruction, 2017,47(4):60-64,110. DOI: 10.13204/j.gyjz201704014. (in Chinese)
[4] Dam T X, Wight J K,Parra-Montesinos G J. Behavior of monotonically loaded slab-column connections reinforced with shear studs[J].ACIStructuralJournal, 2017,114(1): 221-232.
[5] Baig Z I, Alsayed S H, Abbas H. Punching of slab-column connections strengthened using external steel shear bolts[J].MagazineofConcreteResearch, 2016,68(2): 55-68. DOI:10.1680/macr.14.00434.
[6] 张蕾, 刘海峰, 郑鹏, 等. 钢筋混凝土板柱边节点抗震性能试验研究[J]. 建筑结构, 2013, 43(5): 60-64,28.
Zhang Lei, Liu Haifeng, Zheng Peng, et al. Experimental study on seismic performance of RC column-slab edge connections[J].BuildingStructure, 2013,43(5): 60-64,28.(in Chinese)
[7] Kang T H K, Lee J D, Lee B S, et al. Punching and lateral cyclic behavior of slab-column connections with shear bands[J].ACIStructuralJournal, 2017,114(5): 1075-1086. DOI:10.14359/51689780.
[8] Park H G,Ahn K S, Choi K K, et al. Lattice shear reinforcement for slab-column connections[J].ACIStructuralJournal, 2007,105(2):237-238.
[9] 吴艺, 吕西林, 扶长生. 型钢剪力架板柱节点抗震性能研究[J]. 结构工程师, 2016, 32(3): 70-76.DOI: 10.3969/j.issn.1005-0159.2016.03.011.
Wu Yi, Lü Xilin, Fu Changsheng. Study of seismic performances of RC slab-column joints with shear head reinforcement[J].StructuralEngineers, 2016,32(3): 70-76. DOI: 10.3969/j.issn.1005-0159.2016.03.011. (in Chinese)
[10] 龚启宏, 朱强, 梁书亭, 等. 空心板柱结构中柱节点受冲切承载力试验研究[J]. 东南大学学报(自然科学版), 2013, 43(2): 420-424.DOI: 10.3969/j.issn.1001-0505.2013.02.036.
Gong Qihong, Zhu Qiang, Liang Shuting, et al. Experimental study on punching shear behavior of hollow salb-column interior connection[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2013,43(2): 420-424. DOI: 10.3969/j.issn.1001-0505.2013.02.036. (in Chinese)
[11] 赵斌斌. 不平衡弯矩作用下空心板柱节点冲切性能研究[D]. 南京: 东南大学土木工程学院, 2013.
[12] Ingerslev A. The strength of rectangular slabs[J].JournalofStructuralEngineering, 1923,1(1):3-14.
[13] 马云昌, 吕西林. 钢筋混凝土板柱节点的抗震性能研究[J]. 建筑结构学报, 2001(4): 49-54.DOI: 10.3321/j.issn:1000-6869.2001.04.009.
Ma Yunchang, Lü Xilin. Seismic behavior of reinforced concrete slab-column system[J].JournalofBuildingStructures, 2001(4):49-54. DOI: 10.3321/j.issn:1000-6869.2001.04.009 .(in Chinese)
[14] Park R, Gamble W L. 钢筋混凝土板[M]. 黄国桢, 成源华,译.上海: 同济大学出版社, 1992: 193-198.

