四自由度汽车振动模型分析
2018-06-12 06:22张泽鹏李洋徐海升
时代汽车 2018年10期
张泽鹏 李洋 徐海升
山东理工大学 山东省淄博市 255000
1 振动模型的建立与分析
1.1 振动模型的建立
选取一辆乘用车,各参数和数值在表1中给出,为了分析方便做出如下假设:(1)车身是质量分布均匀的刚体。
(2)两侧车轮的运动状态在任何时刻都相同。
(3)车身仅做垂直于地面的上下振动zc和绕质心的俯仰θ。
(4)车轮仅做上下振动z1,z2。
基于以上假设并将将该车简化为四自由度的振动模型如图1所示。
1.2 根据牛顿第二定律对四自由度模型进行受力分析
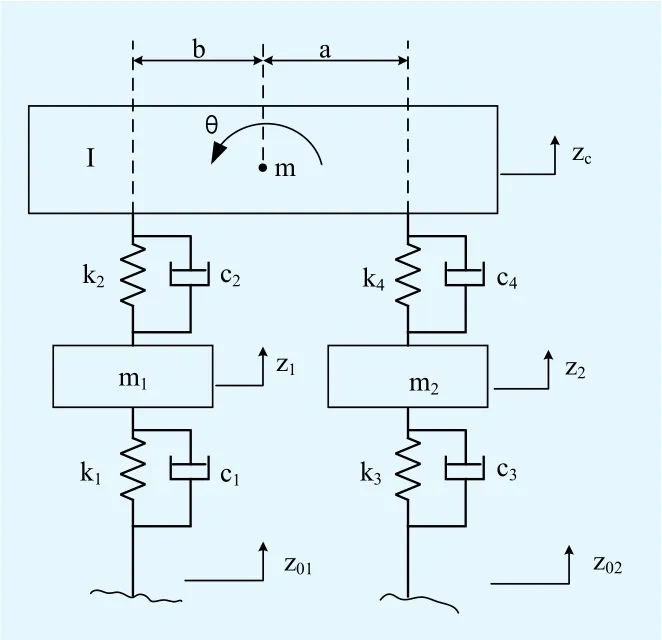
图1 汽车四自由度振动模型
受力平衡:
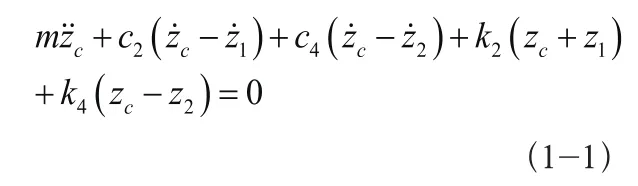
绕之心的力矩平衡:
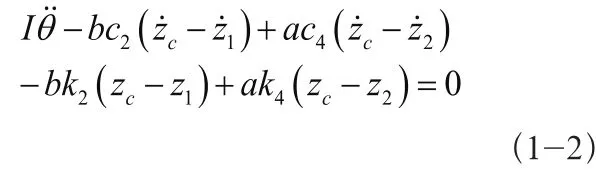
前轴受力平衡:
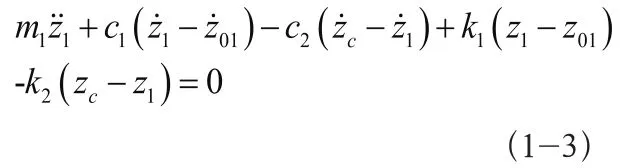
后轴受力平衡:
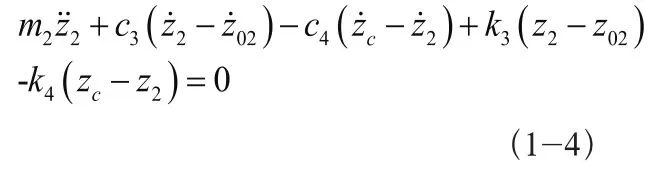
前后轴运动关系:
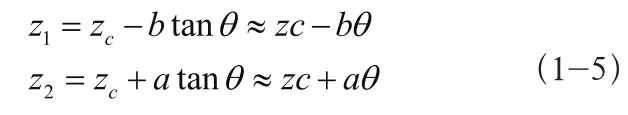
整理得到方程组:
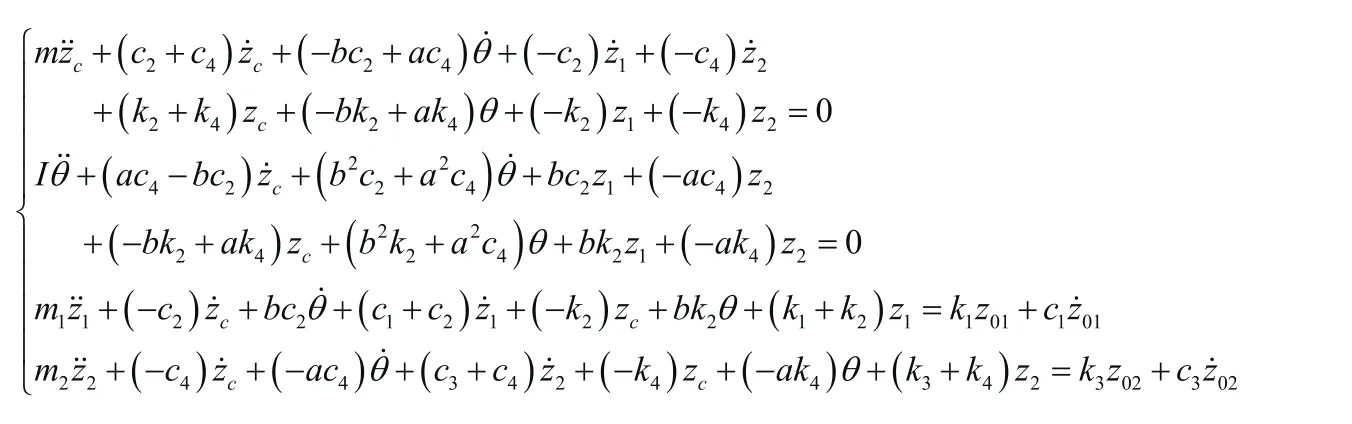
写成矩阵形式:
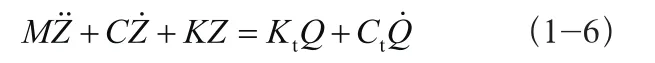
式中:
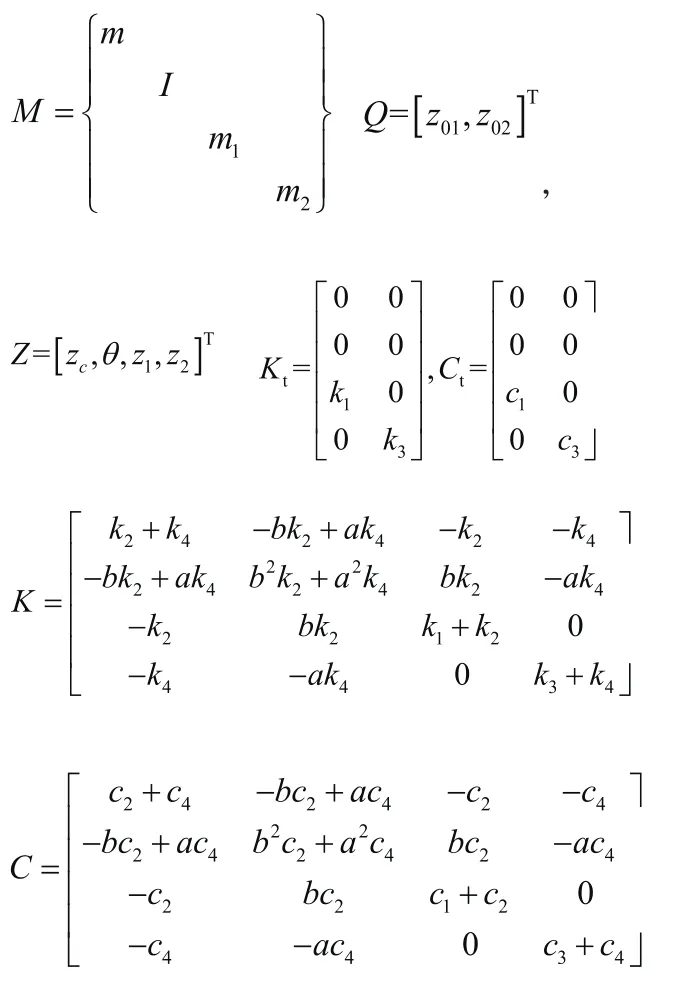
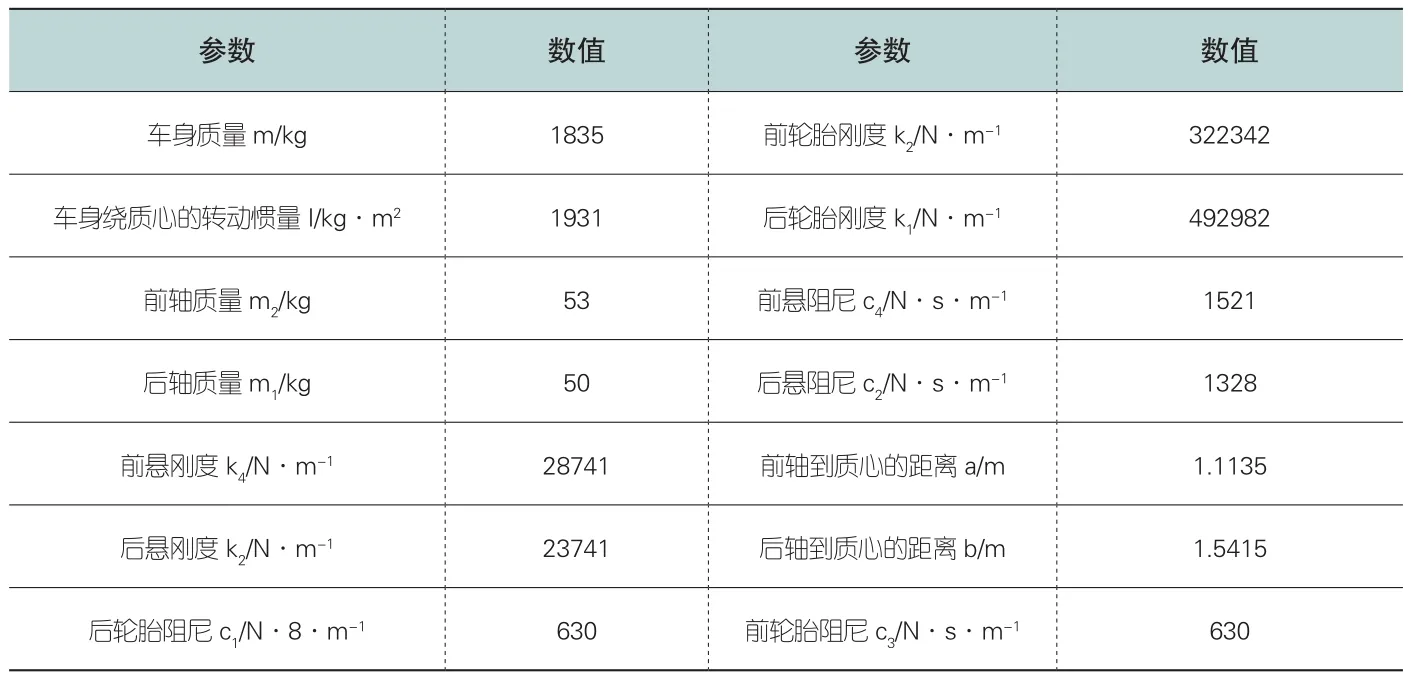
表1 汽车参数
拉普拉斯变换:
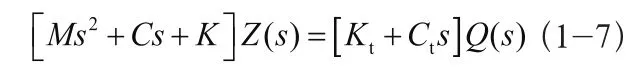
传递函数
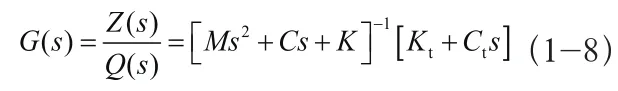
傅里叶变换得到频响函数矩阵
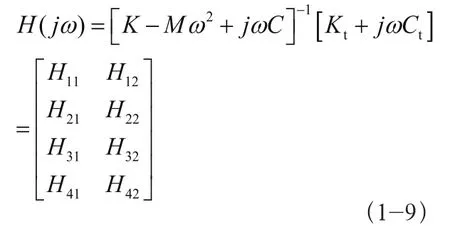
2 模型求解计算
取频响函数矩阵中的H11、H12、H21、H22,利用MATLAB编程绘制幅频特性曲线如图2、图3所示:
令A=M-1K,根据fE-A=0求出矩阵A的特征值f,即为系统的固有频率:
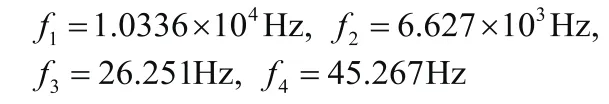
写出特征矩阵:
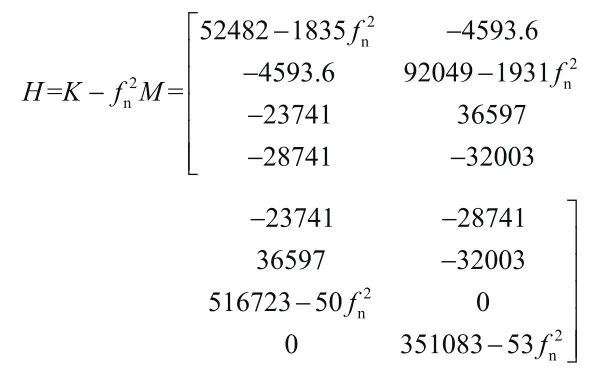
并求出H的伴随矩阵H*
取伴随矩阵的第一列,将四个固有频率分别代入得到汽车振动系统的四阶固有振型:
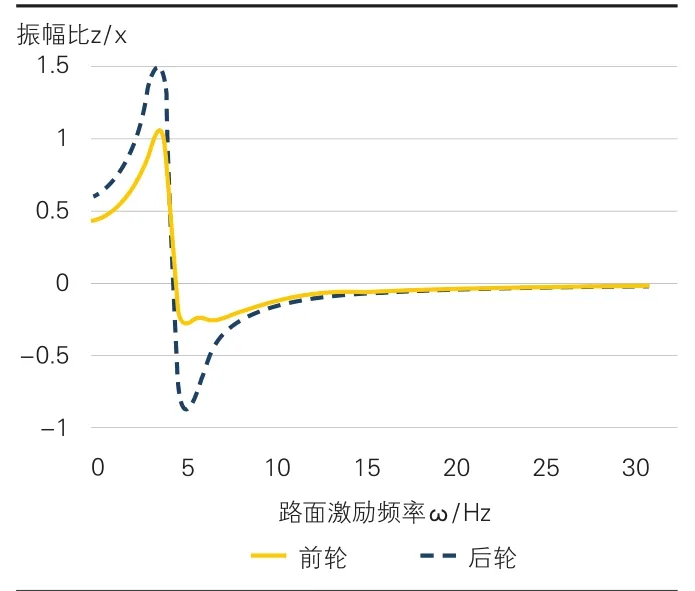
图2 车身垂直振动对前后轮激励的幅频特性曲线
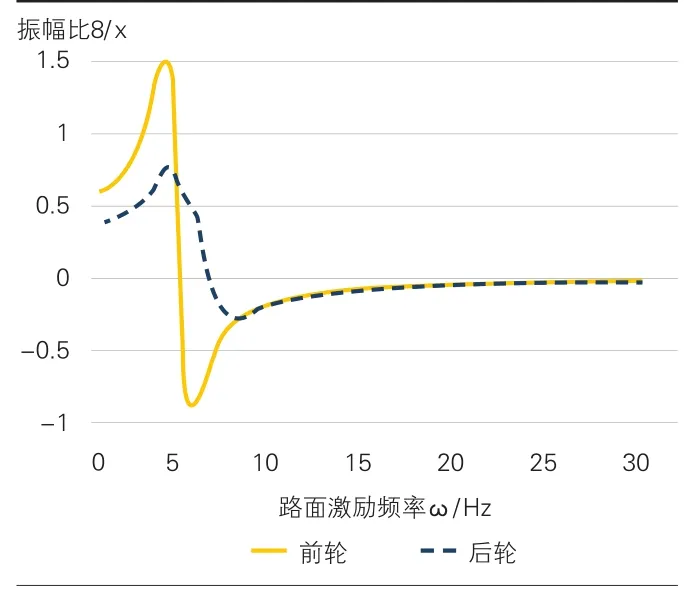
图3 车身俯仰振动对前后轮激励的幅频特性曲线
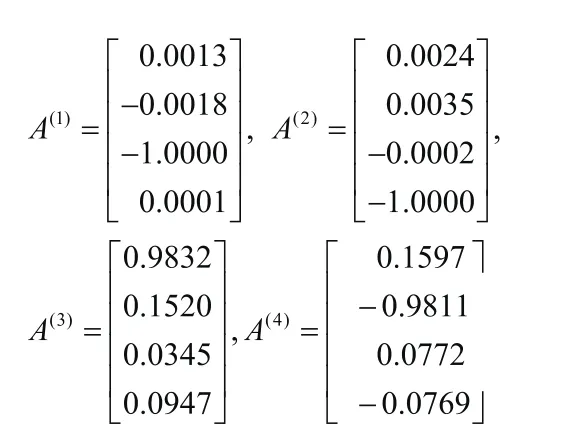
绘出主振型图如图4所示。
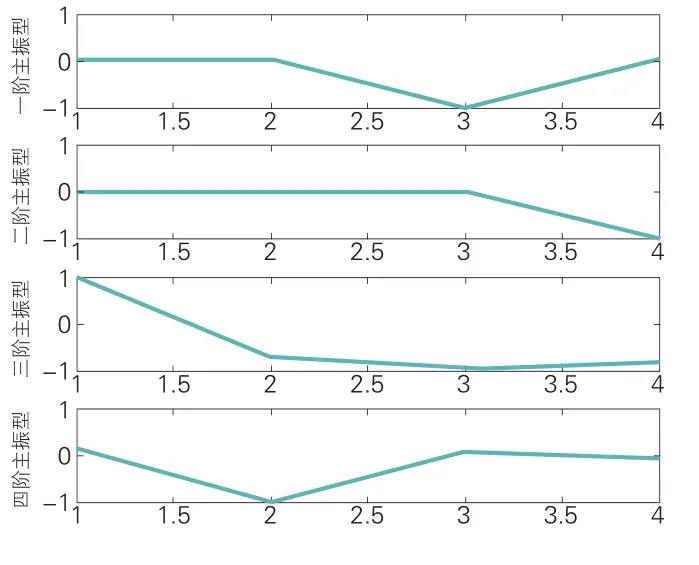
图4
3 主要结论
(1)根据图2和图3可以得知,在后轮的激励对车身垂直振动的影响较大,前轮的激励对车身俯仰振动的影响较大。
(2)路面激励为4.6Hz时,车身垂直振动zc与后轮路面激励的振幅比达到最大值,为1.645,与前轮路面激励的振幅比达到最大值,为1.063。
(3)路面激励为4.8Hz时,车身俯仰角 与后轮路面激励振幅比达到最大值,为0.7842;路面激励为4.6Hz时,车身俯仰角与前轮路面激励振幅比达到最大值,为1.650。
(4)根据幅频特性曲线可知,在行车过程中避免路面激励出现在[3Hz,8.7Hz]的区间内可有效提高舒适性。
猜你喜欢
汽车维护与修理(2022年5期)2022-09-06
小学生学习指导·爆笑校园(2019年6期)2019-09-10
发明与创新·中学生(2017年7期)2017-07-10
股市动态分析(2016年24期)2017-01-07
股市动态分析(2016年23期)2016-12-27
股市动态分析(2016年18期)2016-10-11
股市动态分析(2016年4期)2016-09-29
红蜻蜓(2015年11期)2016-02-02
中国自行车·骑行风尚(2014年4期)2014-10-10

