基于系统动力学的大型体育赛事中食品现场仓库存策略研究——以2014年南京青奥会为例

殷美霞

(同济大学 经济与管理学院，上海　201804)

0　引言

大型体育赛事对食品库存的管理具有较严格的要求，需要及时响应运动员的食品需求，不允许缺货情况的发生。然而，库存问题处理不当容易导致库存堆积、食品浪费或者库存短缺等情况的发生。库存管理通过对库存数量的控制来降低库存成本，对于库存策略的研究则需要以实际需求种类为依据。因此，本文以2014南京青奥会现场仓库存问题为背景，探讨合理的库存管理策略，以满足消费者的需求。

本文以南京青奥会现场仓为研究对象，以系统动力学为研究工具建立模型进行仿真模拟，寻找较优的订货策略，以降低库存成本并且探究订货点和订货周期对库存成本的影响。通过建模仿真模拟系统已经发生的情况及未来有可能发生的情况，以此对实际问题进行改进，以期降低库存成本。

1　国内外研究现状

目前，国内外单独研究食品库存策略的文献并不多，但是有关易逝品库存策略的研究较多。Ghare和Schrader[1]对易逝品的库存策略研究较早，他们利用指数方程来表示因商品变质而导致的库存量随着时间减少的比例关系, 并利用EOQ模型解决随机生命周期易逝品的库存策略问题。Nahmias和Pierskalla[2]在不考虑固定订货成本和提前期的情况下研究了货架期为2的易逝品的最优订货策略，Fries[3]又讨论了货架期为N(N≥2)的情形。Liu和Lian[4]在考虑缺货成本、固定订货成本的情况下研究了易逝品的周期性补货策略。Gaukler等[5]研究了紧急订货情况下的补货策略。田志友等[6]在需求为离散的负二项分布的情况下，利用粒子群优化算法给出了易逝品的最优订货策略。郑长征等[7]基于购买行为特征对需求进行分类，建立了动态规划模型，给出了需求和产品生命周期均为随机变量的情况下的易逝品库存策略，显著提升了零售商的利润，减少了因商品损坏所造成的损失。Jen-ming Chen和Tsung-Hui Chen[8]建立了损耗率服从Welbull分布的易逝品库存管理模型。孙玉玲等[9]在产能固定的情况下，建立了两类客户违约情况下易逝品的超售决策模型并给出了最优订货量。

一些学者也使用了系统动力学的方法进行了食品的库存与供应链策略的研究。Patroklos Georgiadis和Dimitrios Vlachos等利用系统动力学的方法作为食品供应链建模和分析的工具，深入分析了食品供应链的一个关键问题即长期的容量规划问题。E.teimoury和H.Nedaei等建立了系统动力学模型，研究了水果和蔬菜的供应链问题，讨论了供应链中的行为和关系，确定供给、需求和价格的相互作用和影响。于首非建立了冷链物流系统动力学模型，得出在冷链库存控制模型中，需求的微小变动经过层层传递后被放大，直接影响各个环节的需求和库存水平。慕静和马丽丽利用演化博弈理论和系统动力学的方法分析了食品供应链中信息共享的影响因素。杨芳和谢如鹤根据冷鲜农产品订货配送特点，构建了冷链系统中供应商-配送中心-零售商VMI系统动力学模型并给出了最优订货策略。

从中可以发现，有众多研究利用系统动力学模型解决库存及供应链仿真问题，但应用于食品物流领域的较少。本文将结合大型体育赛事中食品物流的特点，建立系统动力学模型并给出优化的库存策略。

2　库存系统的动力学模型

2.1　模型的假设

本文以青奥会现场仓库存系统为背景建立相应的模型，为便于操作，做以下假设：

(1) 现场仓每隔固定时间检查一次库存，并订购商品达到期望库存量，即订货策略为周期盘点策略；

(2) 运动员人数服从均匀分布；

(3) 只考虑一种食品，本文以西瓜为例；

(4) 不允许缺货情况的发生；

(5) 订货周期大于订货提前期。

2.2　库存系统的存量流量图

为了对系统有更加直接的认知及便于建模，对系统的结构说明如表1所示。

表1　系统结构

现场仓库存根据运动员的需求，采用周期订货策略向供应商订货，经过一段时间产品入库，供应给运动员消费，系统需要确定最优的补货策略(订货周期，期望库存)使得库存成本尽量降低。根据系统各要素间的关系，绘制现场仓库库存量流量图，如图1所示。

2.3　变量间函数关系的确定

存量流量图绘制完成之后，需要据此进一步确定各变量之间的具体函数关系式。现场仓每隔一个固定的订货周期检查一次库存并进行订货，订货量为期望库存与现有库存的库存偏差。系统不发生缺货用数学关系式表示如公式(1)(T1和T2分别表示订货提前期和订货周期)：

P(T1+T2期间的需求≤期望库存)=100%

(1)

由于需求服从均匀分布，利用概率论的相关知识求得当期望库存满足T1+T2期间的最大需求量时，可以保证系统不发生缺货。假设运动员人数满足a至b的均匀分布，食品需求量用运动员人数与人均日消费量的乘积来表示。

本文的函数关系式如表2所示。

图1　现场仓库存量流量图

现场仓库存(INV)dINV(t)dt=ER(t)-SR(t)-MR(t)入库速率(ER)ER(t)=RINV(t)T1在途库存(RINV)dRINV(t)dt=OR(t)-ER(t)订货速率(OR)OR(t)=OQ(t)出库速率(SR)SR(t)=DEM(t)需求率(DEM)DEM(t)=P(t)×C运动员人数(P)P(t)=RANDOM(a,b,SEED)变质速率(MR)MR(t)=INV(t)×B订货量(Q)OQ(t)=PLUSE TRAIN(0,0,T2,15)×EISC库存偏差(DISC)DISC=DINV-INV期望库存(DINV)DINV=MD×(T1+T2)

3　参数设置与模型仿真结果

3.1　参数设置

为便于计算，本文只考虑西瓜的库存问题。根据获得的数据对模型的参数进行设置，如表3所示。

表3　模型参数设置

考虑到西瓜的储存时间不超过三天，故在本文中只讨论订货周期为2天和3天的情况(由于订货周期大于提前期，故不考虑订货周期为1天的情况)。

3.2　模型仿真结果

订货周期为2天和3天时，现场仓库存的仿真结果如图2所示。

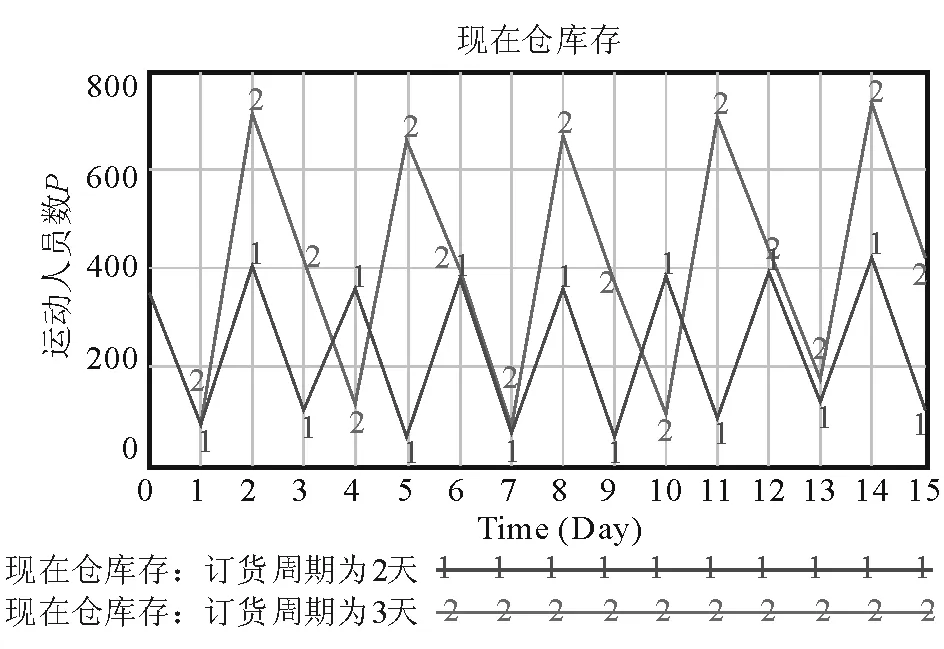
图2　两种订货周期下的现场仓库存变化

各订货周期下每天的库存量及平均库存量见表4。

比较不同的订货策略发现，当订货周期为2天时现场仓平均持有库存最少，没有造成过多的积压，故订货周期为2天是最优的订货策略。

3.3　参数对模型的影响

3.3.1需求对系统的影响

将运动员人数变化为3 500～5 000的均匀分布，增加需求的不确定性，现场仓库存变化如图3所示(订货周期为2天)。

表4　不同订货周期下的现场仓库存量

图3　需求对库存量的影响

从图4可以发现，增加了需求的不确定性之后，现场仓库存的变化并不大，说明该系统较为稳定，并不会因为需求的微小变化而使库存控制策略发生较大的变化。

3.3.2订货提前期对系统的影响

为便于观察订货提前期对库存量的影响，比较订货提前期为1、2、3天的情况如图4所示(以订货周期为5天作对比)。

图4　订货提前期对库存量的影响

从图5发现，系统的库存量随着订货提前期的增长而增长，且变化幅度有增大的趋势。

4　结论与展望

4.1　结论

本文利用系统动力学的方法对大型体育赛事背景下的库存控制策略进行了研究。根据上述仿真结果，可以得出如下结论：

第一，期望库存的设置可以有效调节库存状况，其数值对持有库存水平的影响较大。期望库存的控制应该综合考虑订货周期、订货提前期和需求等因素。

第二，该库存系统受需求变化的影响较小，系统较为稳定。另外，系统状态受订货提前期的影响较大。

4.2　展望

本文仅考虑西瓜这一种食物，而大型体育赛事现场仓中食物的种类繁的多。因此，应该选取其中相对较重要的食品类别来建立库存管理的动力学模型。另外，每类食品的需求、订货提前期等相关参数均不相同，模型需要根据不同对象进行调整。

由于获取数据的局限性，本文仅将平均库存水平作为评价方案的标准，有待进一步改进。运动员需求也仅假设为均匀分布，实际情况中需求可能更为复杂，需要根据实际的需求对库存策略进行相应调整。