基于多重分形理论的股价同步性与噪音关系研究

一、引 言

自Roll［1］提出用R2来反映单个股票与市场同涨同跌的关联性以后，学术界始终在争论低R2究竟是代表了更多的公司特质信息还是更多的噪音，至今这个问题仍然没有定论。Morck等通过比较40个国家的R2，发现产权保护机制完善的国家具有较低的股价同步性，并以此推断：“发达国家因其完善的法规制度使得股价中包含更多的公司特质信息，所以股价同步性也会较低。”［2］随后，Li［3］和Bae［4］的实证结果也支持了Morck等的信息解释。但是随着对股价同步性研究的不断深入，人们发现一些现象是与信息解释相矛盾的，比如股价增发定价、超额波动率等。越来越多的文献也发现，股价同步性低并非是股价中包含了更多的公司特质信息，而是更多的噪音。Black认为交易者往往会将噪音误认为是有效信息并以此为依据进行交易，使得股价中融入了大量噪音。［5］那么，中国股票市场的R2会表现出怎样的特征？是否较低的R2意味着更多的噪音呢？

回顾以往股价同步性研究文献，发现大多是利用线性回归模型进行研究。但近期研究发现，股价同步性与信息效率和噪音之间并非线性关系。［6-7］因此，采用非线性分析方法，理应更契合股价同步性的研究。基于此，本文引入多重分形理论研究股价同步性与噪音的关系，以期获得新的发现。

与已有研究成果相比，本文的进展主要体现在以下三个方面：一是将多重分形理论引入到股价同步性研究，利用交叉相关性检验发现股价同步性与噪音之间存在交叉相关性；二是进一步研究股价同步性与噪音交叉相关性的多重分形特征，确认股价同步性与噪音之间的非线性关系；三是通过滚动窗口分析，量化股价同步性与噪音的交叉相关性，进一步得到其交叉相关性的强度变化特点。

二、文献回顾

Roll利用资本资产定价模型，对个股和市场进行回归得到拟合度R2，并认为R2的高低反映了个股股价中公司层面信息的含量。［1］自此以后，越来越多的学者开始研究R2与股价信息含量之间的关系，并普遍认为R2是信息效率的表征指标，并在此基础之上进行了大量的实证研究，形成了低R2的信息假说。但值得注意的是，Roll在提出特质信息影响股价波动的同时，也承认噪音交易可能会导致股价较高的波动。Morck也曾指出，R2不仅仅只包含信息，还混合着噪音。［2］因此，R2与噪音的关系得到了越来越多学者的关注和研究。

作为低R2噪音假说的代表，West发现，公司层面信息和贴现率无法完全解释股票价格的波动，其原因可能是市场上存在着投机性泡沫、投资者期望不合理以及投资者的非理性行为，由此从理论上推测个股股价的特质波动与市场噪音有很大的关系。［8］

也有一些学者利用新的数据样本或选择更长的年度期间，借鉴或复制了Morck的模型及研究过程，通过实证研究得到了相反的结论。Skaife等考察了6个股票市场的股价同步性对公司信息的解释力度，实证结果表明各个市场的股价同步性的波动并非公司特质信息所致。［9］Alves等利用Morck的R2计算模型研究了1985年至2004年期间40个国家的R2，发现各个国家的R2随着年份的不同而上下波动。而一个国家的产权保护法规政策在各年度都是相对平稳的，因此R2的时序波动使得R2与产权保护之间不存在一个稳定的关系，这是与Morck的研究结果相违背的。［10］Cheng等也利用40个国家的样本数据复制了Morck的研究，但没有得到预期的股价同步性与产权保护之间的负相关关系，反而发现波动率和企业规模对股价同步性有着显著的影响，以此为依据，他们推测市场结构特点可能是各国R2存在差异的原因之一。［11］

由于传统的观点认为较低的R2代表较多的信息含量和较高的信息效率，因此一些学者从考察R2与信息效率之间的关系入手来反证股价同步性的噪音假说。Dasgupta等认为，企业信息环境的改善和丰富的企业特质信息都有助于提高市场参与者对企业未来事件的预测准确率，使得股票收益的特质波动减少，股价同步性上升，即股价同步性会随着企业信息透明度的提高而增加。［12］Li等从信息环境代理指标入手，发现较低的R2意味着较高的价格延迟、知情者交易概率、非流动性水平和买卖价差，因此认为与传统的解释相反，较低的R2应是代表了较差的信息环境。［13］Devos等考察了股价同步性与分析师评级调整后的信息交易波动之间的关系，发现分析师评级调整后，R2较低的个股会受到价格、交易量、收益波动率以及买卖价差更强的影响，研究结果支持噪音假说。［14］

还有部分学者对一些特殊现象进行实证研究，发现这些特殊现象无法用传统的信息假说进行解释。Shiller通过对超额波动率进行研究，发现公司特质信息无法解释超额波动率现象，因而认为噪音是引起股价波动的主要原因。［15］Chan等考察了股票增发定价期间的股价同步性与价格信息之间的关系，实证结果表明股价同步性与股票增发折价程度呈负相关，说明股价同步性越高，信息含量也越多，这与低R2的信息假说是矛盾的。［16］

在中国市场，许多学者也是对低R2的信息假说产生了质疑。孔东民和申睿利用一个零成本投资组合分别考察了低R2的信息假说和噪音假说，结果发现我国股市,低R2代表资产价格中包含了更多的噪音成分。［17］王亚平等的研究结果则发现公司信息透明度越差，股价同步性越低，这也说明较低的股价同步性意味着更多的信息噪音。［18］罗琦和付世俊在研究股权再融资过程中的市场择时行为发现，控股股东的盈余管理行为会向市场释放噪音信息，影响股价波动，导致股价同步性降低。［19］张永任等在分析股价同步性与股价中信息含量关系的基础上，提出股价中信息含量与R2可能存在倒U字型关系的理论假说，并通过实证证实了该假说，进而认为较低的R2既可能是由个股特质信息所引起的，也可能源于更大的噪声影响。［6］林忠国等利用非平衡面板数据进行的实证研究结果也是支持了倒U型的关系假说，认为不能简单地将股价同步性等同于公司特质信息含量。［7］同样支持倒U型的关系假说的还有代昀昊等。［20］

综上所述，国内外研究已经从多个方面证明了噪音信息会对股价同步性造成影响，但具体到股价同步性与噪音之间究竟是怎样的关系，学术界仍未有统一的认识，实证的结果也不尽相同。并且，已有文献指出股价同步性与噪音之间是倒U型关系，这也预示着股价同步性与噪音之间的关系并非是简单的线形关系。因此，已有的依据线性模型得出的实证结论就值得商榷了。本文以2000年至2014年上证50中部分股票的日交易数据为实证样本，运用多重分形理论对股价同步性与噪音之间的关系进行实证分析，检验两者之间关系的线形与否，并将其关系量化，进一步分析股价同步性与噪音的关系时变特征。

三、研究方法

1967年，Mandelbrot［21］首次提出了分形理论，用分数维度的视角和数学方法描述和研究客观事物。为了研究不同数据集的长期交叉相关性，Podobnik和Stanley提出了去趋势交叉相关性分析法（DCCA），在多个领域得到了广泛应用。［22］为探究两个交叉相关的非平稳时间序列的多重分形特征，Zhou结合DCCA方法和MF-DFA方法，提出了多重分形去趋势交叉相关性分析法（MF-DCCA），将DCCA的二阶局部趋势推广到了q阶，用于研究两个同时发生的具有自相关性的非平稳序列之间的相关性及其多重分形特征。［23］在实证方面，张永东［24］、卢方元［25］、宛莹［26］、刘维奇［27］等人分别采用不同方法验证了我国股票市场多重分形的存在，并分析了产生原因。Li等也利用MFDCCA方法发现了短期和长期的WTI原油和期货市场之间的交叉相关性具有多重分形特征。［28］

MF-DCCA方法的基本原理如下［29］：

假设有两个时间序列x（i）和y（i），i=1,2,…,N；N是时间序列的长度。

1.构造新的时间序列

其中，分别为两个时间序列的均值。

2.把时间序列X（i）和Y（i）分成Ns=int［N/s］个不相重叠的子区间，每个子区间的长度为s。因为长度N可能不是子区间长度s的整数倍，为了能保证序列结尾的N-Ns×s的值也考虑在内，对时间序列的逆序做同样的处理。这样就可以得到2Ns个子区间。

3.在每一个子区间λ中，通过最小二乘法用多项式函数xλ和yλ拟合轮廓。对于λ=1,2,…,Ns，局部协方差函数为：

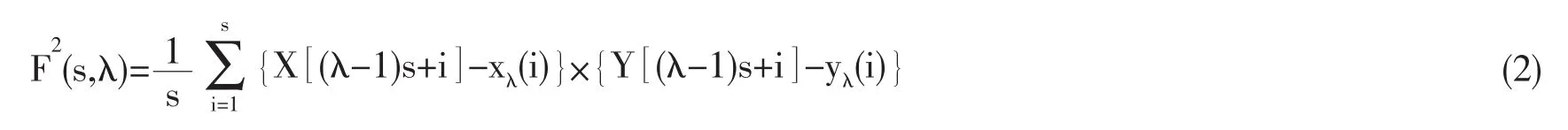
对于λ=Ns+1,…,2Ns，局部协方差函数为：

4.对所有子区间的局部协方差取均值，得到q阶波动函数：

一般来说，q可以是非零的任意实数。当q=0时，根据洛必达法则可以得到：

5.计算不同标度s所对应的波动函数Fq（s）。如果两个序列之间存在长期幂律交叉相关性，则波动函数Fq（s）和时间间隔s存在以下标度关系：

此式另一种表达形式为：

其中，标度指数Hxy（q）即为广义赫斯特指数，是log（Fq（s））～log（s）函数关系图的斜率。

如果Hxy（q）随着q的不同而不同，则两时间序列的其间的交叉相关性具有多重分形特征。当q=2时，Hxy（2）=H为赫斯特指数，H的取值范围为（0,1）。若H=0.5，则表明两时间序列各自不具有长程相关性，即时间序列可以用随机游走来描述，且两者间不存在长程交叉相关性；若0＜H＜0.5，则表明两时间序列各自具有反持久性效应，且两者间具有幂律关系式的反持久性效应的交叉相关性；0.5＜H＜1，则表明两时间序列各自具有长程相关性，且两者间具有幂律关系式的持久性效应的交叉相关性。此外，对应于q＞0，Hxy（q）描述了区间中的大幅波动行为；而对应于q＜0，Hxy（q）刻画了区间中的小幅波动特征。

6.通过MF-DCCA得到的广义赫斯特指数Hxy（q）与多重分形标度指数τ（q）关系如下：

7.若τ（q）与q是线性关系，则两个序列的交互相关关系是单分形的。否则，呈多分形特征。进而通过Legendre变换，得到多重分形谱f（α）：

其中，α是描述时间序列奇异程度的奇异指数。f（α）为多重分形谱，反映了α的分形维数。

多重分形强度可以通过多重分形谱的宽度ΔH来度量。

ΔH越大，多重分形性就越强，市场风险就越大。

四、样本选取与变量定义

（一）样本选择

考虑到数据可得性，研究样本选取2000—2014年上证50中部分股票的日交易数据。股票样本按以下原则进行选择：第一，考虑行业的特殊性，剔除金融保险行业的股票；第二，考虑公司经营情况和财务状况，剔除截至2016年曾退出过上证50成分样本的股票；第三，考虑到数据的可得性和完整性，剔除数据缺失的股票。最终得到17只股票样本。

（二）变量定义

1.股价同步性。根据已有文献［1］［30］，本文通过下列模型对股价同步性进行估计：

其中，rit为第i个公司第t日的对数收益率，rmt为市场第t日的对数收益率。本文研究样本为上证50中的部分股票，因此用上证指数收益率表示沪市市场回报率。对模型（12）进行回归得到拟合系数R2。R2反映了个股股价变动能被市场波动解释的部分，R2即越大，说明股价能反映公司特质信息的含量越少，股价同步性越强。

根据式（13）得到股价同步性的每日波动情况。

2.噪音。梁崴等［31］研究中国股市逐笔交易数据时发现，价差由于同时包含了流动性和信息非对称两方面的信息，对噪音具有较强的解释能力，较大的价差代表较高的噪音水平。刘庆斌和姜薇在研究上证50成分股时也发现价差包含的噪音成分最多。［32］本文借鉴已有成果，利用相对有效价差来反映噪音水平的高低。相对有效价差每日波动情况如式（14）所示。

本文所用个股的R2数据来自于国泰安（CSMAR）数据库，股票价差数据来自锐思（RESSET）高频数据库。

五、股价同步性与噪音的交叉相关性实证分析

（一）描述性统计

限于篇幅，本文仅列出中国石化、中国联通、上海汽车和包钢稀土数据，其他股票具有类似的结论。表1给出了个股股价的R2波动和价差波动的描述性统计。

从表1可以看出，R2和价差波动的Jarque-Bera检验p值均为0.001，在1%的显著水平下拒绝了正态性的原假设，即说明R2和价差的波动序列都不符合有效市场假说中的正态分布假定，都是非正态分布。由表1还可以发现，R2波动序列均呈现出较明显的左偏或右偏特性，峰度值都远高于各自正态分布的峰值，具有尖峰厚尾的分布形态；价差的波动序列的左偏或右偏特性不明显，但尖峰的分布形态则比较明显。

（二）交叉相关性检验

为了从统计学上检验R2和价差两者波动之间是否具有交叉相关性，本文参考Ruan等［33］的做法，采用Podobnik等［34］提出的一种新的交叉相关性检验指标Qcc（m）。

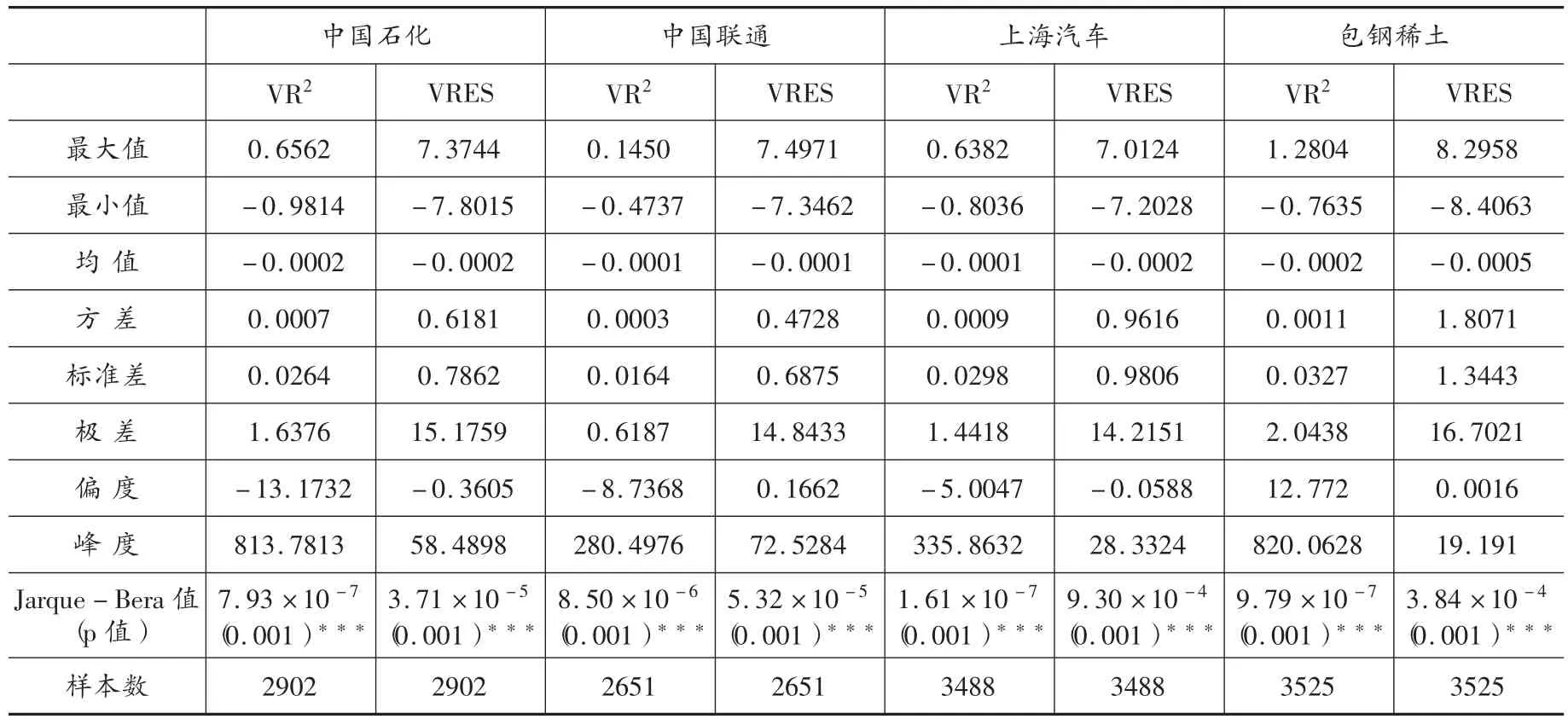
表1 R2波动和价差波动的描述性统计

对于两个时间序列{xt,t=1,2,…,N}和{yt,t=1,2,…,N}，交叉相关性统计检验指标为：

其中，交叉相关函数为：

交叉相关统计量Qcc（m）趋近于自由度为m的χ2（m）。如果交叉相关性检验与χ2（m）吻合，则两个时间序列之间没有交叉相关性，否则两个时间序列之间存在交叉相关性。图1显示了中国石化、中国联通等四只个股的R2和价差的交叉相关性统计量。作为对比，在图中同时作出了在5%置信水平下自由度为m的χ2（m）的临界值，m的值从1取到1000。从图1可以看出，在5%置信水平下，四只个股的R2和价差的波动序列之间的交叉相关性检验统计量均与χ2（m）的临界值不重合，说明R2和价差之间具有交叉相关性。

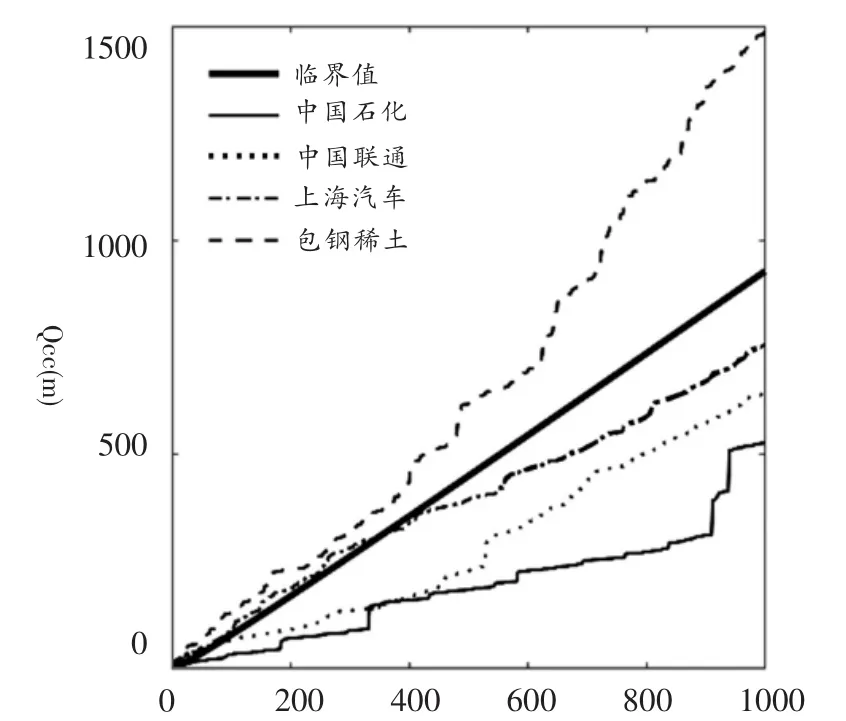
图1 交叉相关性检验统计量

（三）多重分形特征分析

但根据式（13－15）只能定性地检验序列间是否存在交叉相关性。我们将运用MF-DCCA方法量化R2和价差之间交叉相关性的大小，并对其多重分形特征进行分析。

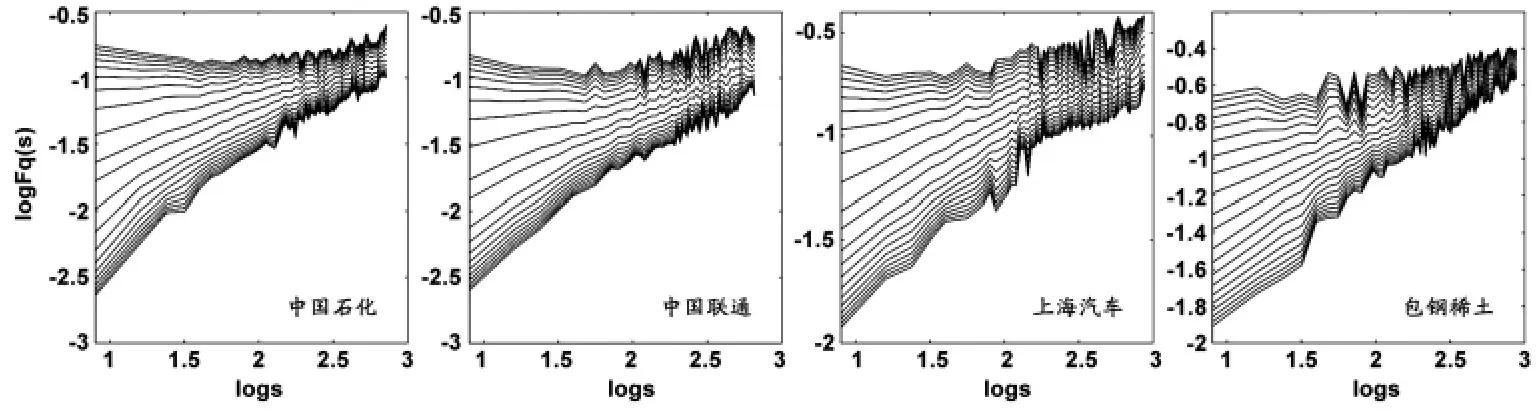
图2 双对数波动曲线图

图2 显示了R2和价差之间的波动函数Fq（s）随着时间标度s的变化而变化的双对数图，设定时间标度s的取值范围为8＜s＜N/4，N为时间序列的长度，波动函数的阶数q以固定步长1在-10到10之间变化。从图2可以看出，对于不同的q值，在一段时期内曲线基本呈现出线性关系，具有较好的幂律关系，这也就意味着R2和价差之间确实存在着交叉相关性。

再根据公式（7）-公式（11），得到R2和价差之间交叉相关性的多重分形特征图，如图3（a,b,c）所示。

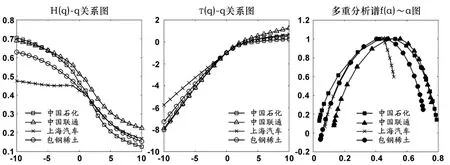
图3 多重分形特征图

由图3（a）可以看出，交叉相关性指数Hxy（q）随q值不同而不同，Hxy（q）均不为常数，这表明R2和价差的交叉相关性具有多重分形特征，这也意味着用单一分形模型对其进行描述是不合适的。而根据公式（6）可知，当q=2时，交叉相关性指数Hxy（q）即为广义Hurst指数。结合图3（a）可以发现，当q=2时，R2和价差的交叉相关性指数Hxy（q）均小于0.5，表明R2和价差的交叉相关性具有较明显的反持续性，即R2增大，价差减小，反之亦然。这意味着较低的R2对应着较多的股价噪音。因此，本文基于多重分形视角的R2与噪音交叉相关性的实证结果支持“低R2代表更多噪音”的已有结论。

根据公式（8），可以得到Renyi指数τ（q）对q值的函数关系图，如图3（b）所示。从图3（b）可以看出，R2和价差的τ（q）都非线性依赖于q，且表现为凸的递增函数，这也证明了R2和价差的交叉相关性具有多重分形特征。

再依据公式（9）-（10），可以计算出Hölder指数αxy（q）和多重分形谱fxy（α），得到R2和价差的多重分形谱f（α）～α图，见图3（c）。如果多重分形谱表现为一个点，则为单分形；否则，即存在多重分形。观察图3（c）可以发现，没有一个多重分形谱是以点的形式存在，这进一步说明R2和价差的交叉相关性具有多重分形特征。其中，αxy的最大值与最小值之差即为多重分形谱宽度△αxy，可以用来反映多重分形的强度。多重分形谱宽度越宽，多重分形强度越大；多重分形谱宽度越窄，多重分形强度越小。正如图3（c）所示，中国石化的R2和价差的多重分形谱宽度最大，这说明中国石化的R2和价差的交叉相关性走势分布更为分散，波动的绝对幅度更大，其多重分形强度在四只个股中最大。

实证样本中，除上述4只股票之外的其他股票也都表现出相似的多重分形特征：R2和价差之间的交叉相关性指数Hxy（q）随q值不同而不同；τ（q）都非线性依赖于q，且表现为凸的递增函数；多重分形谱都没有以点的形式存在。综上所述，R2和价差之间存在交叉相关性，并表现为反持续性，且其交叉相关性具有明显的多重分形特征。

六、滚动窗口分析

已有研究认为，股价同步性与噪音并不存在简单的线形关系。前文利用多重分形方法也证实：R2和价差的交叉相关性存在多重分形特征，通过单一分形模型对两者关系进行描述是不合适的。下面对R2和价差的交叉相关性做进一步的分析，深入研究两者关系的变化特点。

自Cajueiro和Tabak［35］开始，滚动窗口分析就被应用于金融时间数据的研究，以探究外部事件可能的影响。为了得到R2和价差的交叉相关性的日度动态变化，本文也采用滚动窗口分析方法。其中，滚动窗口分析的窗口期长度是滚动窗口分析方法的关键，应适应各种研究的需要而设置。为了捕获到全样本交叉相关性的动态特点，我们借鉴Ruan和Wang［33］的做法，将滚动窗口分析的窗口期设定为250天。首先，我们将时间序列的前250天移除，设定q值为2，计算交叉相关性指数Hxy（q）；然后将样本向前滚动一天，重复上述步骤直至样本末端。通过上述步骤得到的交叉相关性指数Hxy（q）序列如图4所示。

可以看出，R2和价差的交叉相关性指数主要在0.5以下，R2和价差呈反持续性关系，即价差增大，R2降低，意味着当市场噪音增多时，个股股价同步性会减弱，表明较低的股价同步性与较高的市场噪音密切相关。这也与已有关于股价同步性研究中的噪音解释［8］［13］［17］［18］是相一致的。并且还可以发现，虽然R2和价差存在反持续性特性，但其反持续性强度是不断变化的，说明股价同步性与噪音之间的反持续性具有强弱上的波动。因此，由图4可以看出，股价同步性与噪音的关系主要表现为反持续性特征，但其关系强度并非恒定，而是始终处于波动状态。

尽管在大多数情况下，R2和价差的交叉相关性指数在0.5以下。但从图4也可以发现，在个别时期，R2和价差的交叉相关性指数迅速趋近于0.5，说明R2和价差的反持续性非常微弱；甚至R2和价差的交叉相关性指数大于0.5，即R2和价差表现为正持续性，价差增大，R2也增大。这意味着在个别时期，股价同步性与噪音的反持续性变得非常微弱，甚至转变为正持续性，当噪音增多时，股价同步性也相应增强。再将R2与R2和价差的交叉相关性指数结合起来看，又可以发现一个重要现象，即上述的“个别时期”通常是R2发生断崖式下跌时；换言之，当R2发生断崖式下跌时，交叉相关性指数会迅速攀升接近0.5，或是大于0.5。

图4 R2与价差的交叉相关性Hxy（q）及R2

综上，股价同步性与市场噪音并非是简单的线性关联，而是具有多重分形特征的动态非线性关系。在多数情况下，由于噪声、泡沫和非理性行为等因素［8］，股价同步性与噪音主要表现为反持续性特征，即更低的R2意味着更多的噪音。而当股价同步性出现断崖式下跌时，考虑到噪音作用需要一段过程，此时股价同步性的下跌更多是受公司特质信息的影响，且很可能为指向性较明确的特质信息，因此此时噪音相对较少。表现在外，即股价同步性发生断崖式下跌时，R2与噪音的反持续性迅速减弱，或转变为正持续性，噪音随着股价同步性的下降而减少。

七、研究结论及启示

本文从多重分形理论视角，利用交叉相关性检验、多重分形去趋势交叉相关性分析及滚动窗口分析法对股价同步性与噪音的动态关系进行了实证研究，得到了以下结论：

一是较低的R2意味着较多的股价噪音。通过多重分形去趋势交叉相关性分析法得到股价同步性与噪音的交叉相关性指数（q=2）均小于0.5，说明股价同步性与噪音表现为反持续性。

二是通过交叉相关性检验证明股价同步性与噪音之间存在交叉相关性，并通过Renyi指数和多重分形谱发现股价同步性与噪音之间的交叉相关性具有多重分形特征。这也验证了股价同步性与噪音之间并不是简单的线形关系。

三是借助滚动窗口分析，发现股价同步性与噪音的交叉相关性主要表现为反持续性，但其关系强度存在较大的波动性；而当股价同步性发生断崖式下跌时，R2与噪音的反持续性迅速走弱，或转变为正持续性，噪音随着股价同步性的下降而减少。前者从多重分形视角验证了“低R2代表更多噪音”的已有结论；后者关系的变化推测是受公司特质信息的影响而产生。

以上结论对我们思考理性投资和资本市场监管启示如下：

第一，虽然本文的实证结果显示目前中国市场仍是以噪音交易为主，但本文并不否认信息对股价同步性的影响，股价同步性断崖式下跌时的反持续性减弱及转向也说明了信息会影响股价同步性。因此，投资者在分析股价同步性时，要明确是公司特质信息还是市场噪音引起了股价同步性的波动，不能简单的将股价同步性作为公司特质信息或市场噪音的衡量指标。

第二，股价同步性与噪音的反持续性表明低R2代表了更多噪音，意味着上市公司股价的特质波动更多是非理性投资行为的结果。因此，本文结论对证券监管也具有重要的启示：证券监管部门一方面要持续推进证券市场的法规建设和完善信息披露制度，提高信息传递渠道的有效性，减少市场噪音的产生，推动有效市场的建立；另一方面应更积极地规范和引导投资者行为，提高投资者分析和利用信息交易的能力，由噪音交易向信息交易转变，促进市场的理性化。

［1］Roll,R.R2.Journal of Finance,1988,（43）.

［2］Morck,R.K.,et al.The Information Content of Stock Markets:Why do Emerging Markets have Synchronous Stock Price Movements.Journal of Financial Economics,2000,（58）.

［3］Li,K.,et al.Firm-Specific Variation and Openness in Emerging Markets.Review of Economics&Statistics,2004,（86）.

［4］Bae,K.H.,et al.Stock Market Liberalization and the Information Environment.Journal of International Money&Finance,2006,（25）.

［5］Black,F.Noise.Journal of Finance,2012,（41）.

［6］张永任,李晓渝.R2与股价中的信息含量度量［J］.管理科学学报,2010,（5）.

［7］林忠国,韩立岩,李伟.股价波动非同步性——信息还是噪音?［J］.管理科学学报,2012,（6）.

［8］West,K.D.Dividend Innovations and Stock Price Volatility.Econometrica,1988,（56）.

［9］Skaife,H.A.,et al.Does Stock Price Synchronicity Represent Firm-Specific Information The International Evidence.Ssrn Electronic Journal,2006,（3）.

［10］Alves Paulo.,et al.The Use of the R2as a Measure of Firm Specific Information:A Cross Country Critique.Journal of Business Finance&Accounting,2010,（37）.

［11］Cheng,H.,et al.Industry Integration and Stock Price Synchronicity.Social Science Electronic Publishing,2014,（4）.

［12］Dasgupta,S.,et al.Transparency,Price Informativeness,and Stock Return Synchronicity:Theory and Evidence.Journal of Financial&Quantitative Analysis,2010,（5）.

［13］Bin Li.,et al.R2and Idiosyncratic Risk are Not Interchangeable.Social Science Electronic Publishing,2014,（6）.

［14］Devos,E.,et al.Stock Return Synchronicity and the Market Response to Analyst Recommendation Revisions.Journal of Banking&Finance,2015,（58）.

［15］Robert,J.and Shiller.Do Stock Prices Move Too Much to be Justified by Subsequent Changes in Dividends.The American Economic Review,1981,（3）.

［16］Chan,K.and Chan,Y.C.Price Informativeness and Stock Return Synchronicity:Evidence from the Pricing of Seasoned Equity Offerings.Journal of Financial Economics,2014,（1）.

［17］孔东民,申睿.R2、异常收益与交易的信息成分［J］.中大管理研究,2008,（3）.

［18］王亚平,刘慧龙,吴联生.信息透明度、机构投资者与股价同步性［J］.金融研究,2009,（12）.

［19］罗琦,付世俊.股价同步性与控股股东市场择时［J］.中南财经政法大学学报,2015,（1）.

［20］代昀昊,陆婷,杨薇.股价同步性与信息效率［J］.金融评论,2012,（1）.

［21］Mandelbrot,B.B.The Fractal Geometry of Nature.New York:W.H.Freeman,1982.

［22］Podobnik,B.and Stanley,H.E.Detrended Cross-Correlation Analysis:A New Method for Analyzing Two Nonstationary Time Series,Physical Review Letters,2008,（100）.

［23］Zhou,W.X.Multifractal Detrended Cross-Correlation Analysis for Two Nonstationary Signals,Physical Review.E,2008,（77）.

［24］张永东,毕秋香.中国股票市场多标度行为的实证分析［J］.预测,2002,（4）.

［25］卢方元.中国股市收益率的多重分形分析［J］.系统工程理论与实践,2004,（6）.

［26］苑莹，庄新田.股票市场多重分形性的统计描述［J］.管理评论,2007,（12）.

［27］刘维奇，牛奉高.沪深两市多重分形特征的成因及其变化［J］.经济管理,2009,（12）.

［28］Li,J.,et al.Cross-Correlations between Crude Oil and Exchange Markets for Selected Oil Rich Economies.Physica A:Statistical Mechanics and Its Applications,2016,（453）.

［29］Kantelhardt,J.W.,et al.Multifractal Detrended Fluctuation Analysis of Nonstationary Time Series.Physica A:Statistical Mechanics and Its Applications,2002,（316）.

［30］French,K.R.and Roll,R.Stock Return Variances:The Arrival of Information and the Reaction of Traders.Journal of Financial Economics,1986,（1）.

［31］梁崴，王春峰，房振明，张蕊.中国股市微观结构噪音特性及其影响因素——基于逐笔交易数据［J］.系统工程，2009,（27）.

［32］刘庆斌,姜薇.中国股市微观结构噪音与流动性关系研究［J］.统计与决策,2009,（20）.

［33］Ruan,Q.,et al.Cross-Correlations between Baltic Dry Index and Crude Oil Prices.Physica A:Statistical Mechanics and Its Applications,2016,（453）.

［34］Podobnik,B.,et al.Quantifying Cross-Correlations using Local and Global Detrending Approaches.European Physical Journal B,2009,71（2）.

［35］Cajueiro,D.O.and Tabak,B.M.Evidence of Long Range Dependence in Asian Equity Markets:the Role of Liquidity and Market Restrictions.Physica A:Statistical Mechanics and Its Applications,2004,（3-4）.