一种持续侦察无人机集群规模自适应调控方法

井 田 王 涛 王维平 李小波 周 鑫

(国防科技大学系统工程学院 长沙 410073) (jingtiannudt@163.com)

随着无人机系统向着控制智能化、成本低廉化、功能模块化和交互网络化等方向的发展，由多无人机组成、相互协同以完成特定任务的大规模无人机集群(unmanned aerial vehicles, UAVs)越来越成为当下研究的焦点[1].其中，在侦察、搜索、监视等任务中运用无人机集群[2-4]，具有任务的并行性、资源的冗余性、功能的互补性等诸多优点，可以大幅扩展执行任务的范围和能力，并可增加系统的抗干扰能力和鲁棒性[5];与此同时，随着侦察环境越来越复杂和无人机集群规模的不断扩大，如何针对不同的侦察环境，对大规模无人机集群进行数量规模控制逐步成为了亟待解决的问题.

对于多无人机协同侦察，传统的研究方式主要基于环境变化有穷、待侦察目标有限的假设，其研究的核心是控制无人机集群用最短的时间发现最多的目标、使目标发现概率最大化或是覆盖最大的侦察面积[6-7].在这种情况下，通常的策略是无论有多少架可用无人机都尽数出动，以确保短期内侦测效果最大化.

而在一些特殊的情况中，比如民事应用中对森林火灾、河道污染、海上漏油等的灾情监控，对台风形成、风暴移动、海洋汛情等的气象观察[8-9]，军事应用中对战场的频繁空中照相和探测，由于信息在时间域上持续变化，信息的总量可认为是无穷的.单纯将协同侦察行为视为“一次性”的扫描过程难以很好适应需求.如果仍然选择将所有无人机一次性起飞，由于续航能力的约束，随着该批次无人机的降落，很难保证任务的连贯性.同时，不同的目标区域中，由于环境变化速率不同、地形地貌复杂度不同，针对同一个任务所需的无人机集群最佳规模不同.即使在相同的侦察环境中，由于任务的强度不同(如同一个环境中的常规巡逻、区域警戒和战场侦察情形)，如果使用规模恒定的无人机集群，也很难兼顾集群侦察的高效性和经济性.

可以说，无人机集群持续侦察作为一种新兴且极具潜在价值的应用方向，其中所包含的规模优化问题不容忽视.然而，如何针对这一问题进行集群规模调控，在目前的可查的文献中鲜有研究.如何定性甚至定量描述出无人机集群数量与持续侦察的效果的关系，并根据任务环境对无人机集群进行规模配置，成为了一个迫切的问题.在自然界的草皮-食草动物生态系统中，在密度制约等集群演化规律的作用下，生物集群的数量规模自发收敛到使得系统收益率最大的全局最优值[10].与此相似，无人机集群的规模调控问题中，核心问题是在保证效能的前提下获得最佳的侦察效果.在这个过程中，生物集群调节机制所表现出的鲁棒性、自适应、分布式等自组织特征与无人机集群协同控制的要求一致.受此启发，本文借鉴了生物种群的增长和平衡机制[11]，构建了一种基于区域信息熵的“数字草皮”及其“饶度(即丰饶程度)”变化模型(见1.1节).引入种群平衡机制，模仿生态平衡动力学模型[12]，建立了目标区域-无人机集群群落矩阵.通过数学推导描述了该系统的平衡和收敛情况，探讨了描述无人机集群和侦察区域情况的模型以及根据环境、效能和平台性能状态对集群规模进行调配的一种方式并给出了仿真.

1 规模调控问题描述

对特定待侦察目标区域E，无人机集群持续侦察的规模调控问题可描述为：对数量可调整的、执行持续侦察任务的无人机集群U，通过构建环境和无人机模型，确定对于特定环境、在给定的无人机效能约束下，恰好能满足侦察任务要求，并能在连续的时间尺度上维持效能的无人机集群最小数量n.

1.1 环境模型

在持续侦察过程中，环境信息始终在动态、实时地更新，为了便于对侦察的整体效果进行定量分析，有必要建立量化的模型对环境进行描述.

信息熵是Shannon[13]为了解决信息量化度量问题而借鉴热力学定律提出的概念，与信息量互为补偿，对系统的不确定性和无序程度进行了描述.侦察任务的核心是收集环境信息，增强对环境当前状态的确信程度.因此，对于无人机集群持续侦察问题，可将侦察环境视为一个整体，采用环境信息熵描述目标区域E中的环境不确定度并作为侦察整体效果的评价指标，侦察的目的是降低环境的不确定性，即最小化环境信息熵.

同时，注意到环境信息是时敏的，对其变化可归纳出3条规律：

1) 熵增性.对处于无监视状态下的网格，随着时间推移，其环境信息熵逐渐增加.

2) 收敛性.在未被侦察的情况下，当时间趋于无穷时，环境信息熵有最大值，且收敛于特定值.

3) 差异性.对于不同任务环境，其环境信息熵增加速度不同，且变化速率仅与环境本身属性有关.

与上述性质相似，在自然界的草皮作物中，也自发地呈现出相似的性质[14]：在特定区域环境中的草皮，能够不断自我增殖，其总量趋近于环境最大容纳量.与信息的组合性爆炸过程相近，草皮的生长也是不断在上一代基础上增殖迭代的非线性过程.此外，草皮的生长过程还具备多样性和不一致性，不同的草皮作物、在不同的季节中，草皮增长变化情况不同.

类比草皮生长规律，建立用于描述环境信息熵变化的“数字草皮”模型.模型的主要思想是把待侦察的目标区域类比成数字草皮，将环境信息熵的变化过程用草皮生物量的饶度(abundance)a(t)刻画，在未被进行侦察时，环境信息熵的变化服从Logistic规律.

根据设想，得到方程：

(1)

其中，γ是信息的内禀增长率，a是信息熵容纳量.

内禀增长率γ描述环境信息的内生增长速度，描述环境中新的不确定状态从原有不确定状态中孕育的相对速率，如在激烈交战的战区γ值较大，在和平安宁的边境γ值较小.信息熵容纳量K描述环境不确定信息的容纳量，如在人员众多、环境复杂的城市K值较大，在人迹罕至、地形简单的沙漠中K值较小.

1.2 效能约束模型

为了给无人机集群进行最优化调控，需对无人机集群数量进行调控以保证其效能.与环境建模过程相似，为了寻找无人机集群最佳数量规模，将无人机集群视作在待侦察目标区域上空的“数字草皮”草原上觅食的食草动物群体，采取仿生形式对无人机集群自适应规模调控约束进行描述.

集群中无人机通过执行侦察任务体现价值，如果没有侦察任务，则集群中的无人机耗尽自身能源后降落并且不再起飞.若无人机集群中即将耗尽能量的无人机占整个集群的比例恒定，则可将集群视为死亡率为常数的食草动物种群，假设死亡率(集群衰减因子)为λ，有：

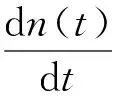
(2)

同时，侦察任务则给集群数量正向激励，使其变化率增加σ2.在无人机集群中，每台无人机的侦测效能不仅与自身性能指标有关，还与无人机集群的密度有关.无人机集群密度越大，单台无人机的效能就越差.在面积固定的待侦测环境中，无人机效能与集群密度负相关.

最终得到集群的规模控制函数：

(3)

其中，λ为衰减因子.等号右边括号内第1项为归一化后集群的自然衰减率，体现对集群数量的效率约束，即在未执行任务的情况下集群规模以λ的相对速率收缩；等号右边括号内第2项体现侦察任务的正向激励,环境中待侦察的任务量越大,对无人机集群规模增长的激励越大，其中，增长的变化率为σ2；等号右边括号内第3项体现密度效应对集群增长的抑制作用，N为无人机集群在环境中的最大容量.

1.3 侦察感知模型

在无人机进行巡航侦察的过程中，影响任务执行效果的主要任务载荷是机载感知模块.如图1所示，假设该侦察无人机采用图像采集模块对环境信息进行捕捉，由于有限视场角限制，每架无人机在单位时间内只能从环境中侦察到有限的情报信息.体现在环境模型中，即数字草皮的饶度将感知模型映射到“数字草皮”环境模型中，式(1)进一步改写为

(4)

其中，等号右边括号内的前2项含义与式(1)相同；等号右边括号内的第3项中σ1为无人机性能参数，表示单位数量的无人机(相对于N)从环境中所消耗的饶度是生成量(不考虑内部消耗)的σ1倍.

Fig. 1 Schematic diagram of reconnaissance system for UAV cluster for “digital turf” model图1 面向“数字草皮”的无人机集群侦察体系示意图

2 基于生态平衡的规模调控方法

为了更好地分析无人机集群侦察体系的整体特性，本节在“数字草皮”基础上，参照自然界生态平衡机制，将群落概念引入无人机集群侦察体系.

2.1 广义群落模型

第1节中，通过将侦察环境模拟成“数字草皮”并在此基础上构建模型，分别对环境、无人机集群数量进行了描述.但是，这种建模仍然不能很好地描述“数字草皮-无人机集群”整体作为一个侦察体系的演化过程.在自然界中，食草动物虽然不会对下一代生育数量进行有意识的调控，却能在整体数量上涌现出对变化环境的高度适应性.受其启发，模仿草皮-食草动物生态平衡的动力学过程，建立“数字草皮-无人机集群”构成的广义群落进行分析：

(5)

在此基础上，生态学中的多种群互作用的密度增长可进一步用Kolmogorov模型[15]进行描述，即：

(6)

其中，上下2个等式右侧为种群的相对变化率，其值同时受到本种群和其他种群的密度影响.式(6)对于无人机集群持续侦察体系而言，意味着特定区域中的集群密度与环境信息熵均值互相作用.

在此基础上，经典的Lotka-Volterra模型[16](L-V模型)用线性化的方式对式(6)中f(a,n)和g(a,n)进行描述，即：

(7)

根据第1节中的“数字草皮”环境建模，对于无人机集群，即有：

(8)

2.2 规模调控与生态平衡

对于无人机集群持续侦察体系，规模调控的目标是求出在特定环境和给定的效能约束限定，恰好能满足侦察任务要求，并能在连续的时间尺度上维持效能的无人机集群最小数量.

在无人机集群组成的侦察体系中，该问题可描述为寻找“数字草皮”群落的生态平衡点.不难分析，在平衡时，“数字草皮”饶度和集群规模变化率为0.对于平衡时调控的平衡点(a∞,n∞)，即：

(9)

对应平衡点可视为方程的常数解，或相平面常数解的轨迹.将式(9)在平衡点(a∞,n∞)处展开，并做变量替换：

(10)

可得

(11)

X′=AX，

(12)

其中，“数字草皮”群落通过系数矩阵A(下称“调控矩阵”)对系统的平衡状态状态进行调控.平衡点处调控矩阵为

(13)

将式(6)中的Kolmogorov模型代入，进一步获得平衡时调控矩阵：

(14)

其中，

A11=a∞fa(a∞,n∞)+f(a∞,n∞),
A12=a∞fn(a∞,n∞),
A21=n∞ga(a∞,n∞),
A22=n∞gn(a∞,n∞)+g(a∞,n∞).

2.3 调控矩阵平衡点及其意义

对于式(12)中的线性系统X′=AX，通过变量的线性变换X=PU(P为非奇异2×2矩阵，描述坐标轴旋转和沿轴尺度变化)，可写为系统PU′=APU，或U′=P-1APU=BU.

该系统与原系统相同，且系数矩阵B=P-1AP，与调控矩阵A相似，因此，可以在相似变换下列出各种可能的标准型来刻画系统X′=AX各种可能的相图，如图2所示.将式(8)代入，可知存在4种可能的平衡点.

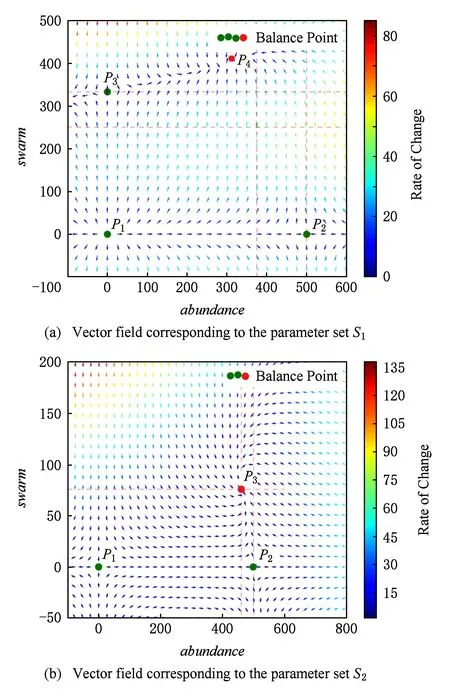
Fig. 2 abundance-swarm vector field diagram图2 饶度-集群相空间方向场图

1) “真空”点：(0，0)，对应调控矩阵

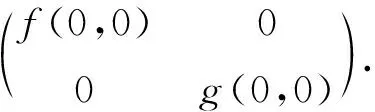
平衡点(0,0)意味着“数字草皮”和无人机群的规模都是0，可以认为是一种真空的情况.这是一种不稳定平衡点，一旦出现微小扰动，例如给“数字草皮”一个初始信息，系统就会远离该点.

2) “荒草”点：(K，0)，对应调控矩阵

点(K,0)是存在待侦察的数字草地而没有侦察无人机介入的情况.在这种情况下，草皮饶度不断增加直到抵达环境最大容量，但该点也不是一个稳定的平衡点，由于捕食-被捕食关系的存在，任何侦察无人机的介入都会使群落偏离该点.

3) “彻知”点：(0，N)，对应调控矩阵

点(0,N)可以认为是一种“彻知”状态，此时环境中无人机过饱和，草皮饶度的增加速度低于无人机群的信息采集速度，因此，“数字草皮”被彻底“吃完”，同时应当注意对于无人机集群，这只是一个理论平衡点，无人机与种群密度负相关，gn(0,N)是负数，该点为无意义的平衡点.

4)“稳定”点：(a∞,n∞)，对应调控矩阵

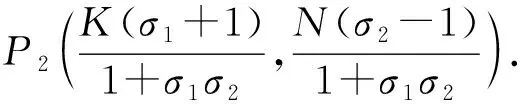
3 实验与仿真

为了验证“数字草皮”环境模型效果，通过仿真手段对基于“数字草皮”群落的变化规律进行了分析.通过方向场图分析了集群规模移动方向，并进行了饶度-集群的时域分析和饶度-集群的相空间分析.

3.1 “数字草皮”饶度模型仿真

根据1.1节提出的“数字草皮”环境模型，假设环境中没有侦察无人机，则目标区域饶度满足Logistic变化规律如式(1)所示.

图3中，取饶度上限K=1 000，内禀增长率γ=1，无人机集群规模n(t0)=0.可以看见，在没有侦察无人机环境中，“数字草皮”饶度持续增长直至达到环境最大容量并稳定.这与1.1节中结论一致.

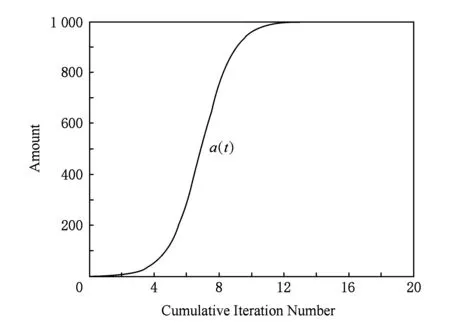
Fig. 3 abundance-swarm scale changing map in time-domain图3 饶度-集群时域变化图(单一草皮)

3.2 群落平衡点仿真

对2.1节中的广义群落模型，利用方向场图对平衡点及收敛性进行可视化表现.参考2.2节中的Lotka-Volterra模型：

(15)

对参数集S={γ，μ1，μ2，μ3，λ，μ4，μ5，μ6}.分别取S1={0.1,1,0.002,0.0001,0.3,1,0.003,0.006}和S2={0.1,1,0.002,0.0001,0.3,-1,0.005,0.003}，可分别作出相空间方向场图如图2所示.

在图2“数字草皮-无人机集群”群落矩阵的方向场图中，可以很好地体现各个平衡点的稳定性.点P1为群落的不稳定平衡点;点P2、点P3分别为2个鞍点、当且仅当群落沿着坐标轴变化才能达到该点，意味着来自另一个种群的任何微小扰动都会破坏这种脆弱的平衡;点P4为一个收敛的平衡点，周围所有的状态都最终收敛到这一种状态，这一结论与2.3节的分析相吻合.

3.3 “数字草皮->无人机集群”耦合仿真

1) 对忽略“种内密度”阻滞效益的无人机集群持续侦察体系进行仿真.如果不考虑无人机集群密度的效能约束和侦察环境中的容量上限约束，原模型将简化为

(16)

分别取γ=1，λ=0.3，K=1 000，N=100，σ1=2，σ2=6，使用Runge-Kutta-Fehberg公式求解方程，可得到增广相空间中的积分曲线如图4所示、相空间中的轨线如图5所示.可看出在理想化不考虑效能约束的情况下，无人机集群规模随着“数字草皮”饶度的变化呈周期性变化而不会收敛到一个平衡点，这种现象类似于自然界中生物群落的周期性变化.

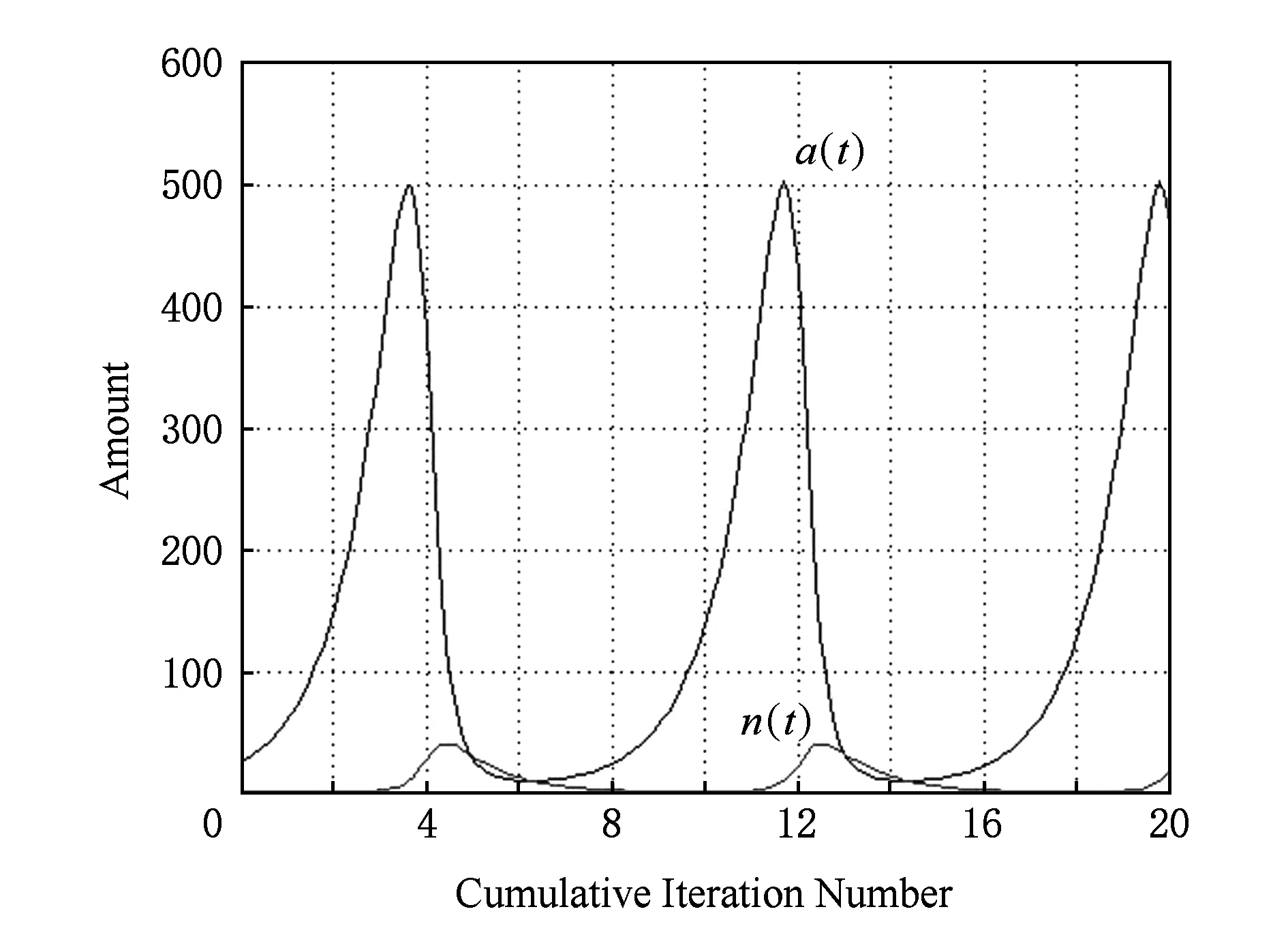
Fig. 4 Integral curve of UAVs in extended phase space without density constraints图4 无密度约束增广相空间积分曲线

2) 基于第1节中提出的有约束“数字草皮”模型，对系统进一步细化.如图6所示，从数值解在时域内的变化过程可看出，集群和环境饶度的数值随着时间的变化逐步收敛，并最终达到平衡.如图7所示，在相平面中，可以看见集群规模和待侦察环境饶度的相轨迹沿逆时针方向逐步收敛到最终平衡点，与图5所示系统不同，这是一个稳定的平衡点，群落到达该状态后不再出现波动，侦察体系在平衡点处达到规模和侦察效能的稳定，而且整个体系有明显的收敛性.

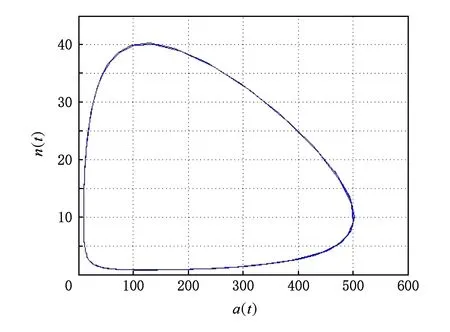
Fig. 5 Track chart of abundance-swarm in phase space without density constraints图5 无密度约束饶度-集群相空间轨线图

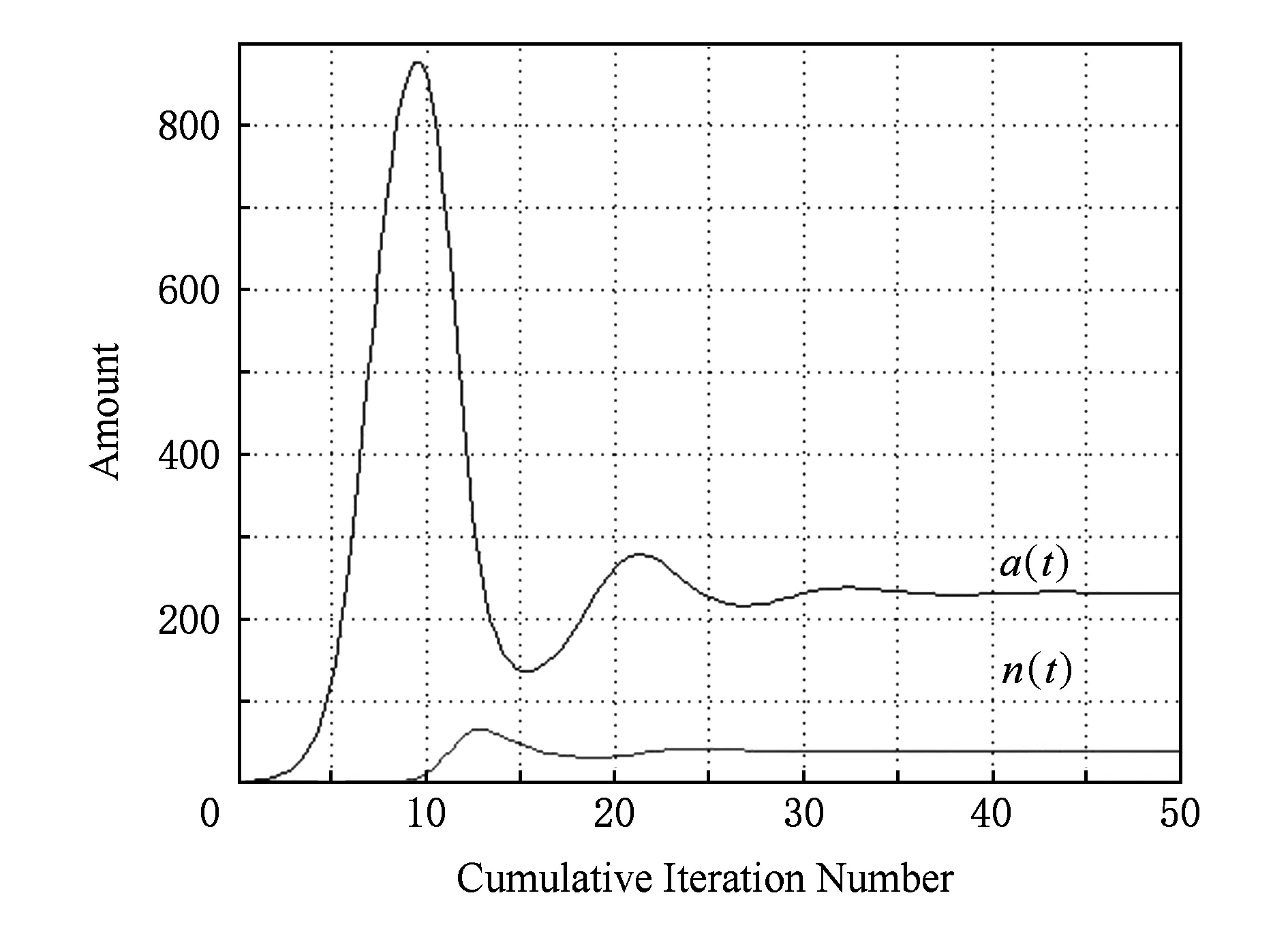
Fig. 6 Integral curve of UAVs in extended phase space with density constraints图6 有密度约束增广相空间积分曲线

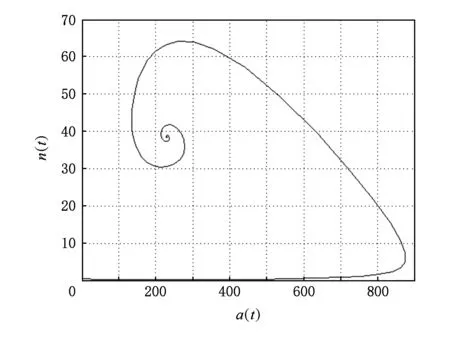
Fig. 7 Track chart of abundance-swarm in phase space with density constraints图7 有密度约束饶度-集群相空间轨线图

3) 为了探讨同一侦察环境中不同初始已知信息或初始集群规模情况下的收敛状态情况，分别选取3种系统的初始状态仿真平衡点的到达过程和验证唯一性，初始状态分别如下：

① 已知初状态全部环境信息(信息熵最小)，无人机集群初始规模最小，取(a0,n0)=(1,1)；

② 已知部分状态环境信息(信息熵较大)，无人机初始规模最小，取(a0,n0)=(500,1)；

③ 已知初状态全部环境信息(信息熵最小)，无人机集群初始规模中等，取(a0,n0)=(1,100).

分别得到集群演化过程如图8～10所示.

分别在图8(a)的基础上改变了环境饶度的初始值和集群的初始规模，从图8(a)～(d)分析中，在改变初始条件的情况下，仅仅会对系统平衡点的建立过程产生影响，对平衡点本身没有影响，整个侦察系统能稳定地收敛到相同的平衡的状态.

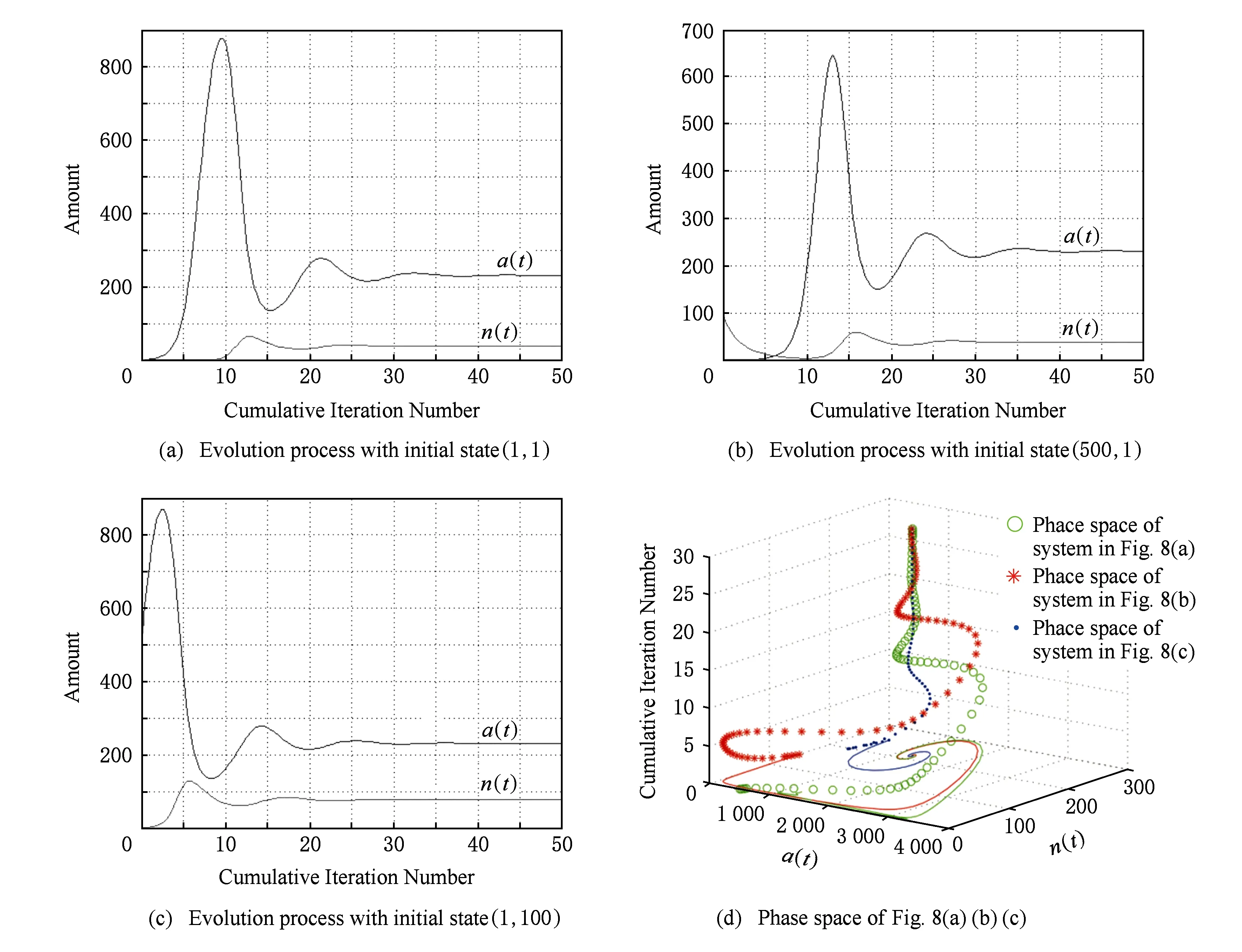
Fig. 8 abundance-swarm changing diagram in phase space and time domain图8 饶度-集群时域-相空间变化图

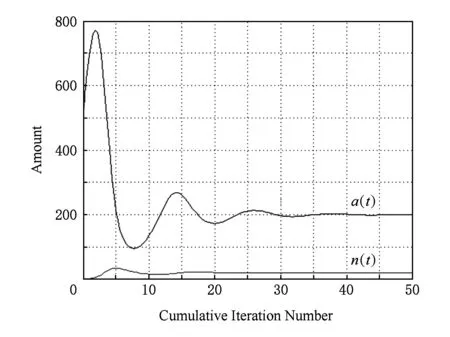
Fig. 9 Integral curve of UAVs in extended phase space图9 增广相空间积分曲线

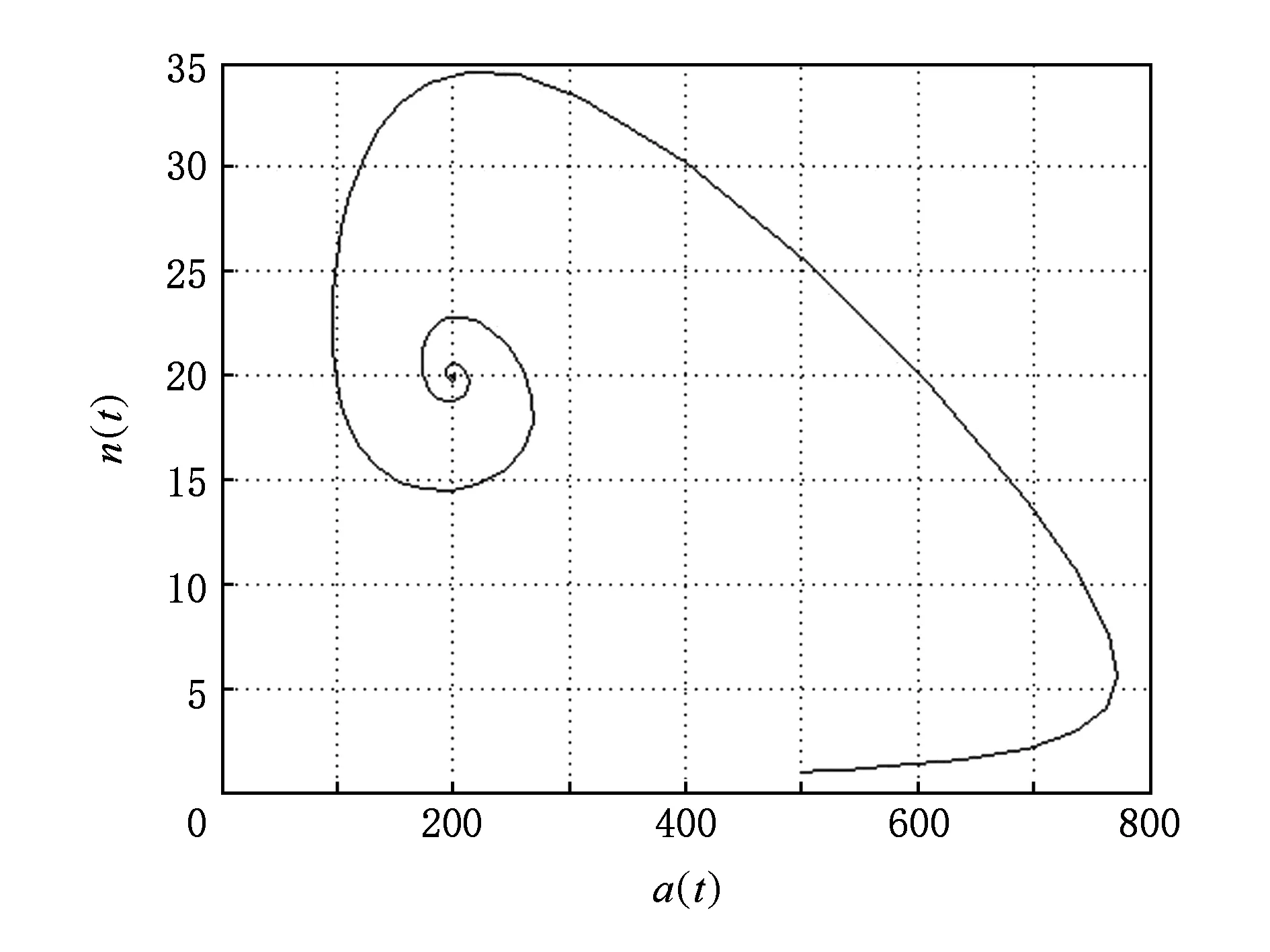
Fig. 10 Track chart of abundance-swarm in phase space图10 饶度-集群相空间轨线图

4) 进一步探讨无人机的侦察效能对最终状态的影响.取饶度初始值500,集群初始值1，增大无人机平台侦测能力σ1=4.

从图9、图10可看出，在改变了无人机侦测能力后，随着收敛的过程，最终的平衡点发生了变化.从图10所示的相轨迹可看出，在增强了无人机能力后，只需更小的集群规模(20台左右而非40台)，就可以把环境的饶度稳定控制在一个更小的范围内(信息熵约200单位而非更多).

4 总 结

随着多无人机协同过程中无人机数量的不断增加，以及以持续侦察为典型的具有时间长、任务复杂特点的使命任务的越来越多，开展对无人机集群规模的自适应调控方法研究具有重要的现实意义.

针对面向动态环境的多无人机巡航侦察问题，本文基于草皮-食草动物生态系统，提出了一种用仿生手段进行集群规模调控的方案.设计了一种基于区域信息熵的“数字草皮”及其饶度变化模型，利用种群动态平衡机制，建立了目标区域-无人机集群群落矩阵，探讨了描述目标区域信息熵和无人机集群规模之间关系的新方法，求解了在效能最优原则下的平衡点，通过仿真手段对平衡点收敛性进行了验证.

[1]Shen Lincheng, Niu Yifeng, Zhu Huayong. Theories and Methods of Autonomous Cooperation Control for Multiple UAVs[M]. Beijing: National Defense Industry Press, 2013 (in Chinese)(沈林成, 牛轶峰, 朱华勇. 多无人机自主协同控制理论与方法[M]. 北京: 国防工业出版社, 2013)

[2]Leahy K, Zhou D, Vasile C I, et al. Provably Correct Persistent Surveillance for Unmanned Aerial Vehicles Subject to Charging Constraints[M]. Berlin: Springer, 2016: 605-619

[3]Peng Hui, Su Fei, Shen Lincheng. Extended search map approach for multiple UAVs wide area target searching[J]. Journal of Systems Engineering and Electronics, 2010, 7(4): 795-798 (in Chinese)(彭辉, 苏菲, 沈林成. 用于多无人机广域目标搜索的扩展搜索图方法[J]. 系统工程与电子技术, 2010, 7(4): 795-798)

[4]Saska M, Vonásek V, Chudoba J, et al. Swarm distribution and deployment for cooperative surveillance by micro-aerial vehicles[J]. Journal of Intelligent & Robotic Systems, 2016, 84(1234): 469-492

[5]Liang Xiaolong, Sun Qiang, Yin Zhonghai, et al. Review on large-scale unmanned system swarm intelligence control method[J]. Application Research of Computers, 2015, 32(1): 11-16 (in Chinese)(梁晓龙, 孙强, 尹忠海, 等. 大规模无人系统集群智能控制方法综述[J]. 计算机应用研究, 2015, 32(1): 11-16)

[6]Lin Lanny, Goodrich M A. Hierarchical heuristic search using a Gaussian mixture model for UAV coverage planning[J]. IEEE Trans on Cybernetics, 2014, 44(12): 2532-2544

[7]Shen Dong, Wei Ruixuan, Qi Xiaoming, et al. Receding horizon decision method based on MTPM and DPM for multi-UAVs cooperative large area target search[J]. Acta Automatica Sinica, 2014, 40(7): 1391-1403 (in Chinese)(沈东, 魏瑞轩, 祁晓明, 等. 基于MTPM和DPM的多无人机协同广域目标搜索滚动时域决策[J]. 自动化学报, 2014, 40(7): 1391-1403)

[8]Bernard É, Friedt J M, Tolle F, et al. Using a small COTS UAV to quantify moraine dynamics induced by climate shift in Arctic environments[J]. International Journal of Remote Sensing, 2016, 38(8910): 2480-2494

[9]Balampanis F, Maza I, Ollero A. Coastal areas division and coverage with multiple UAVs for remote sensing[J]. Sensors, 2017, 17(4): 808-833

[10]Zhang Xinan, Chen Lansun, Neumann A U. The stage-structured predator-prey model and optimal harvesting policy[J]. Mathematical Biosciences, 2000, 168(2): 201-210

[11]Brauer F, Castillo-Chávez C. Mathematical Models in Population Biology and Epidemiology[M]. Berlin: Springer, 2012

[12]Ebner M, Watson R A, Alexander J. Coevolutionary Dynamics of Interacting Species[M]. Berlin: Springer, 2010

[13]Zhou Wei, Li Xiaojing. A comprehensive evaluation method based on information entropy[J]. Science Technology and Engineer, 2010, 10(23): 5839-5843 (in Chinese)(周薇, 李筱菁. 基于信息熵理论的综合评价方法[J]. 科学技术与工程, 2010, 10(23): 5839-5843)

[14]Zhang Caiqin, Yang Chi. Simulation and correlation analysis of meteorological factors and growing dynamic in growing season[J]. Journal of Inner Mongolia Agricultural University: Nature Science Edit, 2009, 30(1): 91-96 (in Chinese)(张彩琴, 杨持. 生长季内草原植物生长动态与气象因子的相关分析及其模拟研究[J]. 内蒙古农业大学学报: 自然科学版, 2009, 30(1): 91-96)

[15]Dai Guoren. Qualitative analysis of Kolmogorov predator-prey system[J]. Acta Mathematicae Applicatae Sinica, 1988, 11(4): 444-456 (in Chinese)(戴国仁. Kolmogorov 捕食者-食饵系统的定性分析[J]. 应用数学学报, 1988, 11(4): 444-456)

[16]Yuan Hailong, Li Yanling. Existence and stability of coexistence states for a Lotka-Volterra competition model[J]. Acta Mathematica Scientia: A, 2017, 37(1): 173-184 (in Chinese)(袁海龙, 李艳玲. 一类具有Lotka-Volterra竞争模型共存解的存在性与稳定性[J]. 数学物理学报: A辑, 2017, 37(1): 173-184)

JingTian, born in 1993. Master candidate of National University of Defense Technology. His main research interests include UAV swarm control and system of systems engineering.

WangTao, born in 1976. Professor and master supervisor of National University of Defense Technology. His main research interests include artificial intelligence and UAV swarm.

WangWeiping, born in 1962. Professor and PhD supervisor of National University of Defense Technology. His main research interests include system of systems engineering and simulation.

LiXiaobo, born in 1983. Professor and lecturer of National University of Defense Technology. His main research interests include system effectiveness simulation and modeling.

ZhouXin, born in 1990. PhD candidate of National University of Defense Technology. His main research interests include Markov decision and UAV mission planning.