基于风险指标的电网设备检修策略评价方法

周强

（国网江苏电力有限公司检修分公司苏州运维分部）

0 引言

对电力设备检修的研究，主要倾向于对其个体的研究，这就造成了检修决策的片面性，同时在对检修时机的决策制定时，由于考虑不全面，可能会对电网的运行带来不良的影响，造成一定的经济损失。检修决策的制定，都是以电网的安全可靠为出发点，同时兼顾经济性原则来实现电力设备检修决策方案的确定。对于计划检修，在电力设备个体性能方面的不全面考虑以及对检修时间的不确定把握，极易造成检修不当的情况。

本文在电力设备故障率评价及电网运行性能评估的研究基础上，从电力设备检修在个体与电网整体间折中的决策进行研究。首先给出了风险指标的定义，然后结合风险指标，综合考虑电力设备在电网运行中的作用，给出了电力设备重要性的评价指标，接着对电力设备状态检修方案的评价方法做了说明，最后以某地电网的现有情况为例进行计算，对检修方案做出理论排序。

1 风险指标定义

对电力设备进行检修的主要目的是通过检修降低电力设备的故障发生率，以提高电网运行的可靠性。对检修策略进行评价，最主要的目的就是通过对检修作用的分析来确定最优的检修策略，以量化的方式对电网运行的损失进行表达，能够方便地确定最优检修策略。在电网运行的过程中，主要有两部分损失：一部分是设备个体损失，另一部分是电网供电不足产生的损失。为了全面地反映电网设备的故障可能性和检修过程中的不确定性，使用风险指标R进行表示：R=R1+R2。

其中电网供电不足产生的损失的表达式为：

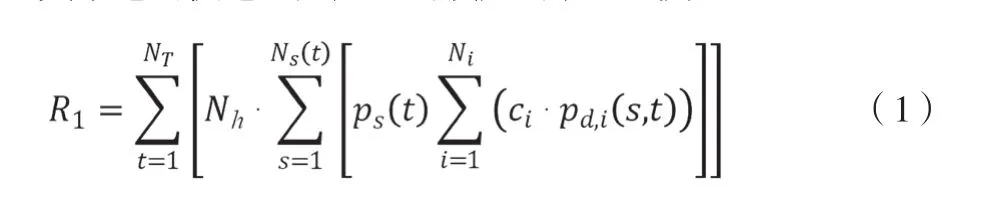
式中，NT为所示周期内划分时间段数量；Nh表示每个时间段的时长；Ns(t)是时间段t内的失负荷电网状态参数；Ps(t)是在时间段t内，状态s发生的概率；Ci表示负荷i的失负荷单位损失值；Pd,i(s,t)为在时间段t内，电网状态为s的情况下，负荷i的失负荷功率。

设备个体损失的表达式为：

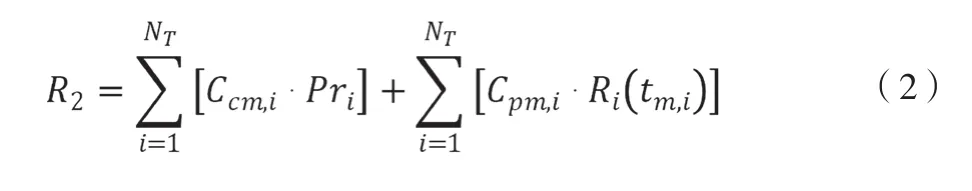
式中，Ccm,i为在设备i出现故障后相应的维修费用；Pri为在相应的时间周期内设备i出现故障的累计概率；Ccm,i表示对设备i预防检修时预估的花费；Ri(tm,i)表示对电力设备i进行检修时，该电力设备安全运行的概率。

电网供电不足时，会产生另一种形式的损失——期望失负荷量。式（1）中的单位失负荷值Ci=1时，期望失负荷量表达式为：

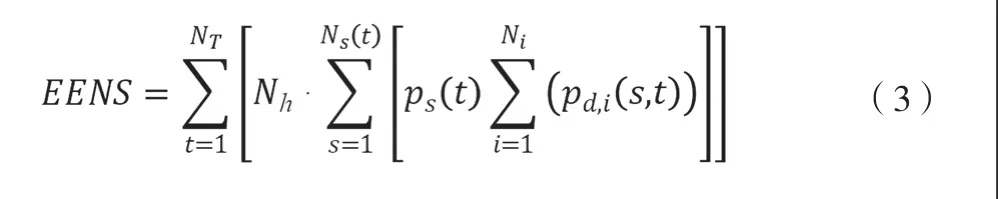
对于电网运行中各节点负荷值的取值，假设在每个时段各节点的负荷功率不变，那么取最高负荷功率值。

2 设备重要性评价

在电力设备检修的过程中，需要重点考虑两方面的因素：一是从电网运行方面出发，考虑设备缺失后运行风险的增量，增量越大说明该设备越重要，对其检修的收益就越大；二是从电力设备个体运行方面出发，若该电力设备的个体性能越差，则其不可用率就越大，说明越需要进行检修。将这两方面的因素综合考虑，给出设备重要性评价的概念。

将电力设备缺失时引发的风险增量和设备不可用率作为评价指标，把电力设备的重要性评价进行量化，以表达式的形式进行展现，得出的值越大说明该电力设备的重要性越强，在进行检修时的理论排序应越靠前。

在时段t内电力设备i停运引发的电网运行风险增量△Ri(t)的表达式为：

式中，Ri(t)为时间段t内电力设备i停运时的风险值险；为时间段t内电力设备i运行时的风险值。

所以电力设备的重要性指标可表示为：

式中，ua,i(t)为时段t内电力设备i的不可用率。

通过计算可以得到待检修电力设备的重要性指标值，根据重要性指标值的大小就可以实现对电力设备进行检修的理论排序。

3 检修方案评价

对电力设备进行检修时，该设备应退出运行，此时电网的运行风险值增加，当完成对该设备的检修后，设备的相关性能得以修缮，故障率会降低，所以对设备的检修需要安排合理的时机，这也是需要进行定量评价的。而且在检修费用受限的情况下，不可能对所有的设备及器件进行检修，对于不同的设备检修方案，需要考虑不同的因素。

在对不同的检修方案进行评价的过程中，主要考虑以下三种关系：一是设备检修与故障间的关系，如果检修前该设备已经故障，则该设备属于故障后维修，没有出现预防检修的情况；二是设备运行状态与预防性检修间的关系，如果到检修时设备没有因故障而停运，那么在检修时该设备就是停运检修状态；三是设备的故障率与检修间的关系，在文中假设出现故障的设备在维修后都能够恢复所有功能，而预防性检修则是不完全修复。

4 算例分析

结合苏州某地区电网现有状况进行算例分析。依据各节点对应的负荷种类对各节点失负荷所引发的单位失负荷价值进行设定：一类负荷是5.053万元/MWh，二类负荷是1.053万元/MWh，三类负荷是0.053万元/MWh。若是某负荷节点含有不止一种类型的负荷，则根据不同负荷在其中的所占比进行计算，求出各种负荷相应的单位期望失负荷费用损失。然后利用相应的方法对该地区110kV及以上电网结构的风险进行分析，所得结果如表1所示。

表1 电网运行风险分析

从表1中的数据可知，系统的供电可靠性=（1年期望切负荷量/系统年总供电量）100%=（1611.77MWh/17520000MWh）100%=99.9965%，得到的系统可靠值高于国网公司要求的城市供电可靠值，说明该地区电网110kV及以上电网的供电可靠性较好。

当电力设备因检修而退出运行时，继续对电网风险指标进行计算，因为电力设备的故障率变化相对缓慢，所以在计算风险值时假定电力设备的故障率是不变的，而四个设备的不可用率依据以往统计结果分别给出如下值：0.002、0.005、0.001、0.003。计算结果如表2所示，从表中数据可以看出各个电力设备的重要性指标差异很大，这主要是有两方面因素造成的：一是受各个电力设备个体性能的影响，二是各个电力设备在电网中的作用不同。该指标对电力设备检修的需求进行了量化处理，给出了检修的理论排序，方便指导检修工作的实施。

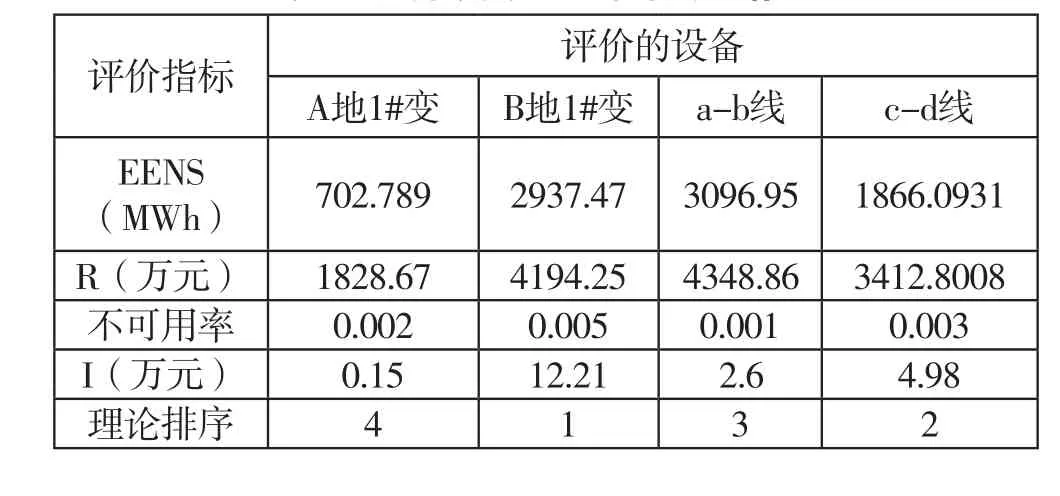
表2 设备缺失后电网的风险指标

5 结束语

电力设备的检修不仅与个体性能有关，而且与电网整体运行有关，为了实现对电力设备检修策略的评价，得出检修的理论排序，文章基于风险指标的理念，结合电力设备个体及电网整体运行的关系，量化定义了电力设备运行风险指标，同时量化给出了电力设备重要性的指标，并对检修方案的评价进行了说明，结合某地电网进行算例分析，对检修方案做出了理论的评价排序，方便检修工作的实施。

[1]韩帮军,范秀敏,马登哲.基于可靠度约束的预防性维修策略的优化研究[J].机械工程学报,2013,39(6):102-105.

[2]赵渊,周家启,周念成,等.大电力系统可靠性评估的解析计算模型[J].中国电机工程学报,2016,26(5):19-25.

[3]宋晓通,谭震宇.基于自适应算法的电力系统可靠性评估[J].清华大学学报(自然科学版),2017,47(s1):1040-1044.

[4]王晓滨,郭瑞鹏,曹一家,等.电力系统可靠性评估的自适应分层重要抽样法[J].电力系统自动化,2014, 35(3):33-38.

[5]程林,郭永基.可靠性评估中多重故障算法的研究[J].清华大学学报(自然科学版),2011,41(3):69-72.

[6]石文辉,别朝红,王锡凡.大型电力系统可靠性评估中的马尔可夫链蒙特卡洛方法[J].中国电机工程学报,2015,28(4):9-15.

[7]束洪春.电力系统以可靠性为中心的维修[M].机械工业出版社,2009.

[8]魏少岩,徐飞,闵勇.输电线路检修计划模型[J].电力系统自动化,2016,30(17):41-44.