双位组合四探针法与常规四探针法的对比研究

王倩

(中国电子科技集团公司第四十六研究所，天津300220)

薄层电阻是指一块正方形薄层沿其对边平面方向的电阻。我们通过外延生长、杂质扩散工艺或离子注入掺杂工艺在单晶衬底上形成一层异型薄层(如在N型衬底上形成P型层或在P型衬底上形成N型层)，或通过真空蒸发工艺、溅射工艺在绝缘材料上覆盖一层金属薄膜。这些结构的薄层电阻值在半导体器件和集成电路生产中都是需要受到精确控制的重要工艺参数。半导体薄层电阻的大小取决于薄层中掺入杂质的情况。当杂质分布形式确定后，通过测量薄层电阻就能推算出表面杂质浓度。

在半导体工艺中，广泛使用四探针法测量薄层电阻。四个针尖排在一直线上，测量时电流由外侧两根探针流经薄层（因薄层与衬底的掺杂型号相异，电流基本上不通过衬底），并用两根内侧探针测量电压。用四探针法测试半导体电阻率时，当被测样品厚度值不能满足理论上提出相应的要求时，必须对测试值加以“厚度修正”。设W为被测样品真实厚度，一般以cm为单位。在进入测量过程后，探针间距S(探针间距平均值)就起着重要作用(如图2所示)。被测样品的厚与薄，是与S相比较而言，S成为度量厚度的单位，厚度在此是个相对概念。所以我们在这里令a代表以S为单位的相对厚度：即a=W/S，(a为无量纲值)。所以，当要进行“厚度修正”时，厚度修正函数将表现为a的复杂函数。同理，在样品边界附近测量时，探针距边界的距离也应以S为基值来衡量，是否要进行边界修正，与S值也有密切关系。

1 四探针法测试体电阻率的两种原理

1.1 常规直排四探针法

常规四探针法是目前测量半导体电性能参数应用最广泛的一种方法，它具有使用方便，测量准确度较高等优点。但该方法也有不足之处，实践中要求所使用的探针头的探针间距应相等，对探针的游移率要求严格。材料的几何尺寸与探针间距相比应满足半无穷大条件。如果上述条件不能满足，则要对电阻率的表观测量值进行修正。

1.2 双位组合四探针法(简称双位法)

双位组合四探针法(简称双位法)是范德堡测量方法的原理在直线排列四探针上的具体应用，它消除了探针间距不等及被测样品几何尺寸对测量结果的影响，所以该方法目前受到国内外相关人士的高度重视。

按其组合方式的不同分为潘氏（Perloff）双位法[1](V23-I14和V24-I13)和宿氏双位法[2](V23-I14和V34-I12)。前者是美国人 D·s·Perloff于 1981年提出，后者是1979年由我国北京工业大学宿昌厚先生提出，两者的差别在于测量时电流电位探针组合方式不同。其中第一次测量，探针组合方式和常规四探针相同。第二次测量，潘氏（Perloff）双位法（见测量原理图1（c）），第二次测量时把电流接在l#、3#探针上，测量2#、4#探针之电压；而宿氏双位法（见测量原理图1（b）），第二次测量是把电流接在1#、2#探针上，测量3#、4#探针之电压。

图1 三种四探针法设计原理

2 理论分析

2.1 测量时电流在不同厚度晶片内分布及流向

以测量薄样片为例 (500 μm厚度以下的样品)，电流在样品里的分布及流向如图2所示。电流在薄层中呈平行状态（平行于样片表面)向两边发散(针尖下面极小区域除外)。

图2 测量电流在厚度≤500 μm薄晶片中的分布和流向

而在厚的样品中(635 μm以上的样品)，电流的分布及流向呈发射状态，如图3所示。

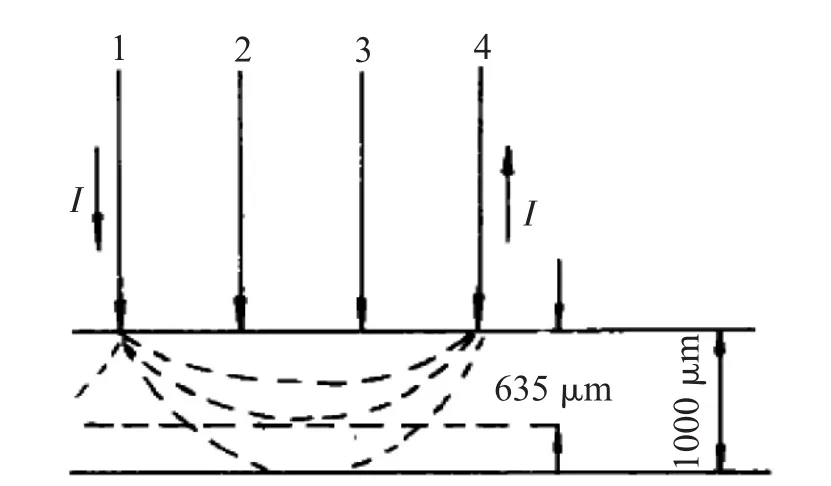
图3 测量电流在厚度≥635 μm厚晶片中的分布和流向

由于电流在厚、薄晶片中的分布状态不同，所以电压探针距与电流探针的距离不等时（见图4），其电阻的测量结果是不相同的。

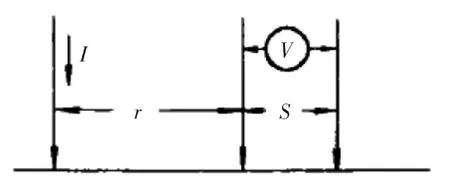
图4 测量结果与位置的示意图

2.2 公式推导

无论是宿氏双位法还是潘氏（Perloff）双位法在测量电路上与常规四探针方法的差别，主要在于组合测量时，探针的电流接线和电位接线是在不同位置上 (双位法第一次测量与常规法相同)，因而造成电位接线两端所测电压的不同。

电压探针与电流探针间的距离r的变化，对电压探针测量结果是有影响的，这种影响薄片样品明显地小于厚样品。这一结沦由前面的测试结果也得到证实。在三种方法的测量结果中，样品厚度在635 μm以上时，双位法的测量结果都比常规法的电阻率大。

潘氏（Perloff）双位法中，见图 1（c）中，2#、4#探针测电压，其距离比其它两种方法测电压的距离大1倍，随着样品厚度的增加，电流流向和分布更趋向呈发射状态，这样该方法所测电压降将有变小的趋势。

潘氏双位法的计算公式为：

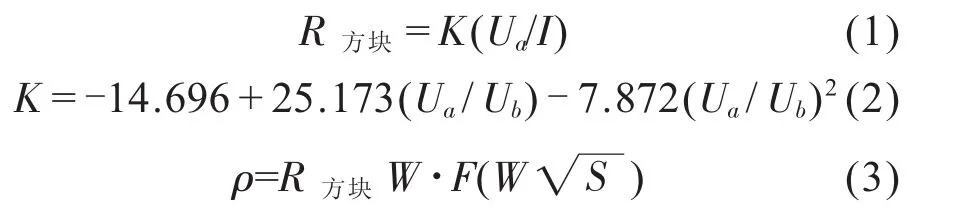
式中，Ua为常规测量法所测的电压降；Ub为潘氏双位法所测的电压降，W为样品厚度值；F(W/S平均）为样品厚度修正系数，K为修正因子。因双位法测量时将U0视为参考基准值，所以从以上公式可知，因Ua值减小，导致Ua/Ub比值增大，在一定范围内K值变大，使得电阻R方块电阻值增大，最终导致电阻率值增大。

宿氏双位法同样存在上述问题，但因它的电压探针3、4两针的间距比潘氏法间距小1倍，受电流状态影响就小一些，所以宿氏双位法所测电阻率值比潘氏法略小一些。

3 总 结

从上述分析可看出，三种方法中，因常规四探针法是测量电阻率较成熟的方法，且其厚度修正系数比较可靠，测量结果更接近样品电阻率的真值，故在测量较厚的样品时(如厚度在1 000 mm左右)应以常规四探针法为准，对于双位法，从对比看宿氏法比潘氏法要可靠。

当然目前在计算厚度修正时，所用的修正系数对常规四探针是较为准确而有效的。对于双位法直接用该修正系数，还得考虑它的合理性。但在双位法建立起自己的修正系数以前，也只能按目前的办法暂时借用，如果以后双位法有了自己的厚度修正办法，半导体材料电阻率的测量准确度可能有一个较大的提高。

双位组合法是准确测量薄层电阻R方块的新四探针测量技术，由于能够自动地完全消除探针间距及其机械游移和样品几何边界的影响，明显提高了测量准确度。双位法测量较厚样品电阻率新计算方法的解决，使得双位四探针法这项新的测量技术在应用范围方面有了新的突破，甚至可能使双位法完全取代常规四探针法，从而使半导体材料电阻率测量的准确度再上一个新台阶，测量结果的不确定度将小于1%。目前，国内最高电阻率测量不确定度为1.5%。

另外，对于探针针头的要求放松，将会使仪器的制造成本有所下降。总之，双位法测量技术是半导体测试的新发展。它的普及和应用，将使半导体材料测试及相应的仪器制造进入一个新的、更现代化的阶段。

[1] Perloff D S.，Gan J N.，Wahl FE.Dose accuracy and doping uniformity of ion implantation equipment[J].Solid State Technology，1981，24(2)：112-120.

[2] 宿昌厚，鲁效明.双电测组合四探针法测试半导体电阻率测准条件[J].计量技术，2004，(3)：7-9+27.