A Particle Filter Based Compressive Sensing Method for Tracking Moving Wideband Sound Sources

Juan Wei＊ , Fengli Yue, Runyu Li, Wenjing Wang, Dan Gao

School of Communication Engineering, Xidian University, Xi’an 710071, China

I. INTRODUCTION

The unattended microphone array is a technology for tracking airborne targets including helicopters, missiles, and airplanes at low- flying areas which is beneath the coverage area of radars [1,2]. Extending the issue for tracking moving targets to other array systems such as the distributed MIMO system [3] will also be a very promising research direction. The essential prerequisite for tracking airborne targets is the direction of arrival (DOA) estimation.

In general, two methods may be used for the DOA estimation of narrowband sound sources, beamforming method and spatial spectrum estimation method. Conventional beamforming (CBF) [4] method presents the advantages of simplicity and good robustness to noise. However, CBF method provides poor spatial resolution and side-lobes contamination [5,6].

To overcome the drawbacks of CBF method, various techniques have been proposed including minimum variance distortionless response (MVDR) beamforming [7] as modified version of CBF to obtain higher spatial resolution, Multiple signal classification (MUSIC)algorithm [8] and estimation of signal parameters via rotational invariance techniques(ESPRIT) algorithm [9]. However, all these techniques suffer from different drawbacks.MVDR beamforming method suffers from the heavy computational burden due to the fullrank matrix inversion. MUSIC and ESPRIT algorithms are two kinds of classic spatial spectrum estimation methods, but the performances of the two algorithms depend on the priori information of sources number, the large amount of snapshots and the relatively high signal to noise ratio (SNR), which are hard to achieve in practical applications.

In this paper, a particle filter based compressive sensing method is proposed for tracking moving wideband sources.

In the other side, various techniques have been proposed for the DOA estimation of wideband sound sources including maximum likelihood estimation (MLE) method [10]and signal subspace method. However, MLE method suffers from requiring a priori information on the number of sources impinging on the array, which is hard to achieve the global convergence and the heavy computation due to the multidimensional search. Signal subspace method has relatively lower computational complexity, including incoherent signal subspace method (ISSM) [11] and coherent signal subspace method (CSSM) [12]. ISSM divides the wide frequency band into some narrowband frequency bins and processes them separately. The estimated DOA may be achieved by combining the weighted results of the frequency bins. However, ISSM may present poor performance or even failure for coherent signals. CSSM is proposed mainly for coherent sources, but its performance is significantly affected by the accuracy of previous estimation on the source directions.

Recently, compressive sensing (CS) [13,14]has been proposed as a revolutionary theory in signal processing, and has been widely applied to many practical applications including medical and ultrasound imaging [15,16], error correction in channel coding [17], radar detection [18], seismic imaging [19], and image reconstruction [20]. Moreover, CS has been extended to DOA estimation [21,22,23] and acoustic imaging [24]. The basic idea of CS is to reconstruct sparse signals from very few measurements with help of convex optimization or greedy algorithms. It has been found that CS is robust as it may provide super-resolution results. Malioutov et al. [25] studied the performance of CS beamforming DOA estimation with respect to the noise, sources number and coherence, to show the superiority of CS beamforming method. Edelmann and Gaumond [26] compared the CS beamforming method with CBF using collected towed-array data at sea, showing the pronounced superiority of CS beamforming method over CBF even with undersampling.

Since the moving airborne targets are usually wideband sound sources, it is required to extend the CS to moving wideband sound sources. Xenaki and Gerstoft [22] reported the limitations of CS applied in frequency domain for wideband DOA estimation. Boufounosa et al. [27] showed that the spatial aliasing appears at some frequency bins and the resolution is proportional to the frequency, namely low frequency leads to low resolution. The spatial aliasing by the uniform linear array and the compressive sensing algorithm results from computing a discrete estimate of a continuous Fourier transform. After sampling, the discrete spectrum becomes periodic with the sampling frequency. The spatial aliasing occurs when the bandwidth of the signal exceeds half of the period of the discrete spectrum.Therefore, there is a challenge for CS to be employed in tracking moving wideband sound sources.

Recently, particle filter [28] has been proposed to approximate the posterior probability density distribution by flooding the state-space with particles. Particle filter is an effective algorithm for tracking sound sources [29,30,31].Valin et al. [30] proposed a steered beamforming along with particle filter algorithm for artificial robot localization and tracking moving sound sources. For tracking multiple moving speech sources, Kijima et al. [31] adopted a Gaussian mixture model on kernel density estimator for the likelihood estimation and introduced an individual particle group for each Gaussian model.

In this paper, we present the particle filter based compressive sensing method for tracking moving wideband sound sources. First, the initial DOA estimates are obtained by wideband CS algorithms. Then, the real sources are approximated by a set of particles with different weights assigned. The kernel density estimator is used as the likelihood function of particle filter. We show by numerical simulations that the spatial aliasing is disappeared and the offset at end fire is reduced by the proposed method. It also shows that the proposed method can achieve satisfactory tracking performance regardless of using uniform or random linear array.

The paper is organized as follows. Section II introduces the observation model for the CS used in DOA estimation for wideband sources,and a brief review of CS theory is described here. Section III presents the proposed tracking algorithm using particle filter based compressive sensing. Experimental demonstration and discussion about the results are provided in Section IV. Finally, Section V concludes the paper.

II. BACKGROUND

2.1 Observation model

In this work, we assume a linear microphone array consisting of M acoustic sensor nodes,and K wideband sound sources in the far field of the array. The location of the source is characterized by the DOA of the associated plane wave with respect to the array axis, i.e.θ ∈[− 90°,9 0°]. The observation area is discretized into N gridpoints (N ≫K, N ＞M),, and every point is viewed as a potential source. The observation model is shown in figure 1, where L is the size of the array aperture, the solid pentagrams represent the real sources and the hollow pentagrams represent the gridpoints without the real sources. It is assumed that the grids are selected fine enough, so that the real sources can be viewed as being reasonably close to some of those grid points. The unknown vector x ∈ RNcomprises the source amplitudes at all N gridpoints. The nthentry of x is equal to zero if there is no source at θn, otherwise it is non-zero.

Considering the narrowband case, the propagation delay from the nthpotential source to every microphone is described by the steering vector

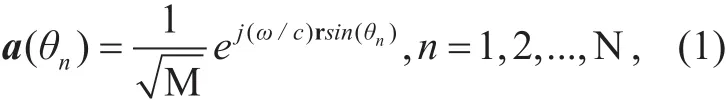
where ω is the angular frequency, c is the speed of sound sources, andcomprises the locations of sensors. So the sparse model is described as

where

A (ω) =is the measurement matrix, and x(ω) ∈ CNis the representation of unknown vector x in frequency domain, y(ω) ∈ CMis the vector comprising the measurements of M sensors in frequency domain.

When considering additive noise e(ω) ∈ CM, the sparse model Eq. (2) is changed to

The observation model is corresponding to the narrowband sources. The wideband sound sources share the same observation model for all frequency bins, so the wideband observation model can be treated as separated narrowband problems. We assume that they are independent and uncorrelated between dif-ferent frequency bins in the paper. Therefore,we don’t consider the interferences between different narrowband problems for tracking moving wideband sound sources. We denote the received signal for the jthnarrowband frequency bin as

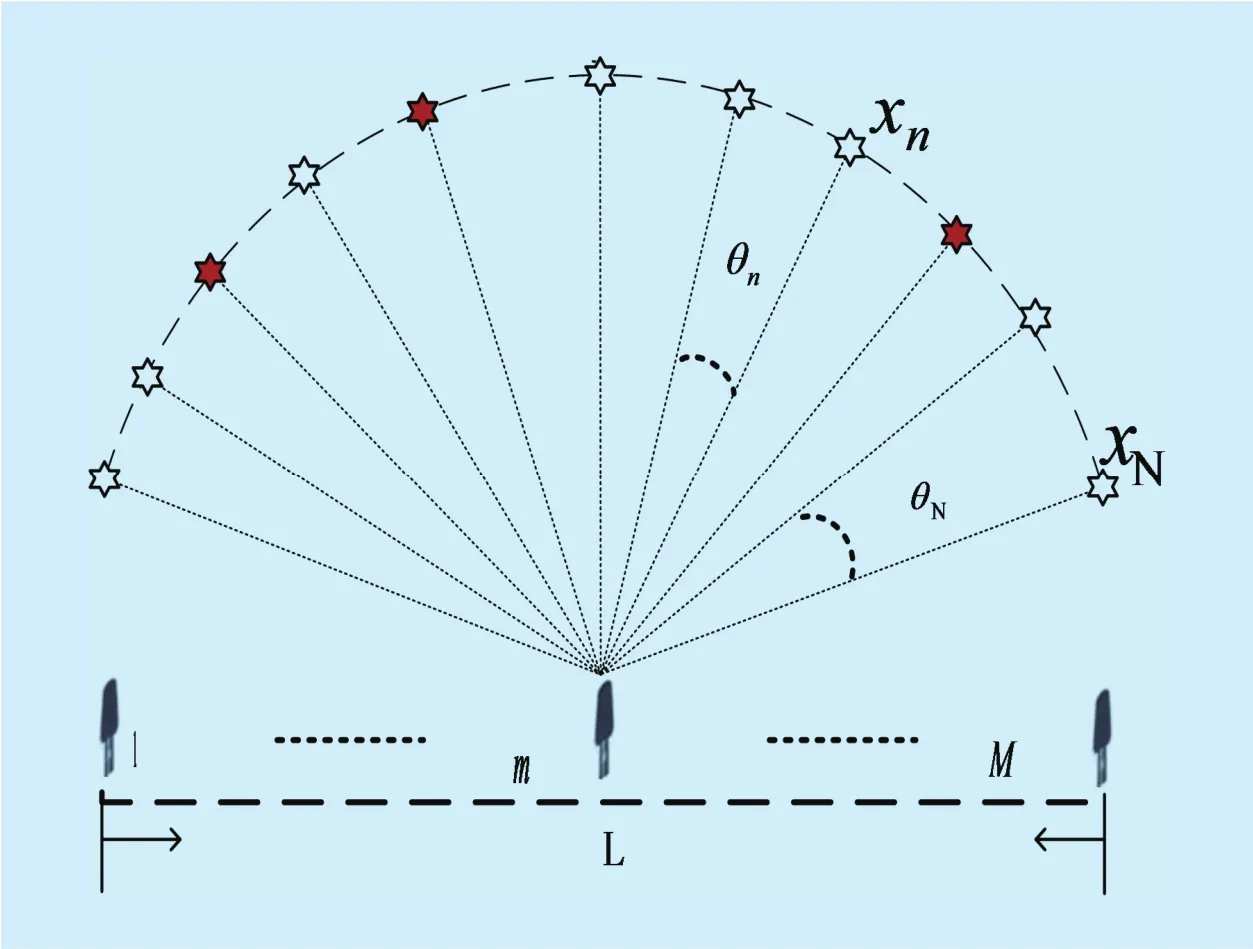
Fig. 1. The observation model of the DOA estimation for narrowband sound sources.

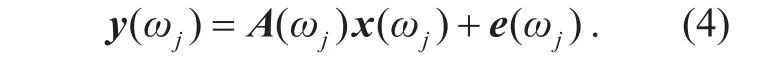
2.2 Compressive sensing

Mathematically, since the Eq. (4) is severely underdetermined, there is usually no unique solution. Moreover, algorithms can be very unstable when the data is corrupted even slightly by noise. Fortunately, owing to the sparsity of the signal, one can recover x perfectly by solving a convex optimization problem

where the l0-quasinormcounts the number of non-zero entries of x, ε is a specified tolerance for noise e.

However, the Eq. (5) is an NP-hard problem, which is computationally intractable.The breakthrough of CS comes with two constraints, sufficiently sparse signals and the sufficiently incoherent column of measurement matrix A. Therefore, Eq. (5) is equivalent to the following l1-optimization problem

where

There are two major types of CS reconstruction algorithms. One is Basis Pursuit(BP)algorithm [32,33], which solves the problem by linear programming methods with polynomial computational time. The other is greedy algorithm, such as orthogonal matching pursuit (OMP) [34], Compressive Sampling Matching Pursuit(COSaMP) [35], Subspace Pursuit (SP) [36], and Iterative Hard Thresholding (IHT) [37]. Greedy algorithm presents the advantages of easy implementation, fast convergence and low complexity [38]. In this paper, we will employ OMP algorithm to solve the sparse model as Eq. (4).

Compared to traditional DOA estimation methods, CS has superior performance especially under challenging scenarios such as coherent arrivals and single-snapshot data.However, the performance of CS is significantly affected by the measurement matrix.It is proved that the measurement matrix A with sufficiently incoherent column is hardly satisfied in lower or higher frequencies for wideband case. For the uniform array, spatial aliasing appears in higher frequencies, so the real sources are usually undistinguished. Xenaki et al. [22] also showed the spatial aliasing with grating lobes within the Gram matrix,which is defined asThe columns or equivalently the rows of G represent the beam pattern for the corresponding focusing direction. Grating lobes appear when d/λ ＞1/2, where d is the array space of a uniform array, λ is the wavelength of the sound sources. The random array is an effective way to solve the spatial aliasing problem, but it may increase the coherence of the measurement matrix. Boufounos et al. [27]found that the resolution is proportional to the frequency, namely low frequency leads to low resolution, due to the higher column coherence of the measurement matrix A regardless of uniform or random arrays.

III. PARTICLE FILTER BASED COMPRESSIVE SENSING METHOD

In general, the spatial aliasing at higher frequencies and the poor resolution at lower frequencies are main obstacles for CS applied in wideband DOA estimation. Besides, CS cannot provide information about moving sources in time. Fortunately, it has been proved that particle filter is an effective way for tracking moving sound sources. Due to these reasons,we propose particle filter based compressive sensing method for tracking moving wideband sound sources.

At time t, we can get the observation data from the microphone array. Adopting CS on DOA estimation at every narrowband frequency bin, we can obtain the setcomposed of the sparse solutions. The non-zero entries are corresponding to the potential direction angles

where B is the number of non-zero entries.

For tracking moving wideband sound sources, I weighted particles are used for every source to approximate the posterior distribution of the DOA. The prediction of the particles with the source dynamic model and the update of weights with the observation model are two main processes of particle filter. For convenience, we only consider the kth source for detail description of the algorithm.

3.1 Prediction based on the source dynamic model

The source state is described by the source dynamic model. We use a source dynamic model with constant velocity. The source state at time t is defined as

whereandare the direction angle and the angular velocity of the source respectively.

The source dynamic model with constant velocity is

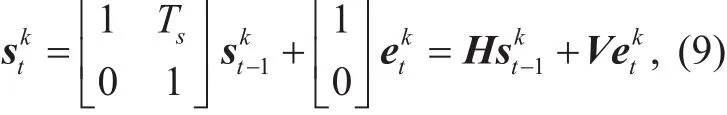
where Tsis the time interval of the adjacent state,is the zero-mean white Gaussian noise with a varianceempirically determined in practice.

According to the Eq. (9), the distribution of particles is predicted by the source state at previous time. The prediction direction angle of the i th particle is sampled by

whererepresents for the mean value of the sound source DOA, θt−1represents for the sound source DOA at t-1 moment andrepresents for the angular velocity of sound source at t-1 moment.

3.2 Update with the observation model

In particle filter, the likelihood function plays a significant role in the estimation of the posterior probability distribution. Inspired by [29],we employ the kernel density function K( θ)as the likelihood function. Since the kernel density function can simulate a kind of probability density function with foreshortening effects, which is approximate to the thought of particle filter. The likelihood function is given as

where h is the window width of one-dimensional kernel density function K( θ) and we choose Gaussian function as the K( θ).

Based on the Eq. (11), the current weight corresponding to the ith particle of the source can be updated as

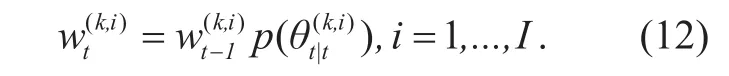
The normalized weightis given as

Next, resampling the particle according to the normalized weights as follows

After resampling, all the weights are updated again asFinally, the DOA estimation can be calculated by average equation

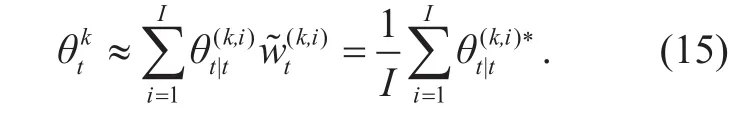
Table I. The proposed algorithm for tracking moving wideband sound sources.

Now we can summarize the particle filter based compressive sensing method for tracking moving wideband sound sources as in table I .

IV. SIMULATION AND RESULTS

The linear microphone arrays with the uniform and random configuration are used for the tracking system respectively. Figure 2 describes the geometry of a uniform linear array and three random linear array configurations.Both of the configurations are composed of 12 sensors. The sensors in uniform linear array are placed 0.85m apart, so the aperture size L= 9.35m. The aperture size of the random linear array is the same as the uniform linear array and its sensors are randomly distributed from 0m to 9.35m. The SNR is 40dB and the number of the gridpoints is N=1801.

Fig. 2. Configuration of linear array. (a) uniform linear array , (b) random linear array I , (c) random linear array II , (d) random linear array III .

In this paper, we assume that the speed of the wideband sound sources in air is 340m/s.The frequency spectra of the wideband sound sources are uniformly distributed between 100Hz and 340Hz. Moving wideband sound sources with linear and sinusoidal motions are considered. We assume that the DOA velocity of the source iswith linear motion andwith sinusoidal motion. The sources are active in time interval from 1s to 90s and Ts=1s . The number of particles is 1000.

4.1 Uniform linear array

The simulated experiments contain a single sound source with linear motion and the array is the uniform linear array in figure 2(a). The source moves from 0°to 90°.

Figs. 3(a), 3(b) and 3(c) show the DOA tracking using CS beamforming method for the narrowband sound source at frequency of 100Hz, 250Hz and 340Hz respectively. It shows that there are obvious spatial aliasings at the frequencies of 250Hz and 340Hz, while there is no spatial aliasing at frequency of 100Hz. Because the value d/λ of the narrowband sources at the frequency of 100Hz,250Hz and 340Hz are 0.25, 0.625 and 0.85 respectively, the grating lobes within the Gram matrix appear at 250Hz and 340Hz.

Figure 3(d) shows that the DOA tracking using the proposed method for the wideband sound source. It shows clearly that the spatial aliasing is disappeared, proving that the proposed method provides a good tracking for the moving wide band sound source. The reason is that the directions of spatial aliasing is different between every frequency bin and the proposed method explicitly takes this into account. Another explanation is that the weights of the particles close to the direction of spatial aliasing are close to zero.

4.2 Random linear array

Employing the random linear array is a simple way to solve the spatial aliasing problem.We analyze the performances of the proposed method for tracking the single wideband sound source using three random linear array config-urations in figure 2. Table II shows maximum error comparison of DOA tracking for the single wideband sound source with linear and sinusoidal motions using the proposed method. It shows that the random linear array II corresponding to the figure 2(c) has the smallest maximum error. Therefore, we use random linear array II for analyzing the performance of DOA tracking in the rest parts of the paper.

4.2.1 Single moving source

There are simulations about single sound source with linear motion and sinusoidal motion. The source with linear motion moves from 0°to 90°. The source with sinusoidal motion moves from 45°and the period of motion is 40s.

Figs. 4(a), 4(b) and 4(c) show the DOA tracking using CS beamforming method for the narrowband sound source with linear motion at the frequencies of 100Hz, 250Hz and 340Hz respectively. Figs. 5(a) and 5(b) and 5(c) show the DOA tracking using CS beamforming method for the narrowband sound source with sinusoidal motion at the frequencies of 100Hz, 250Hz and 340Hz respectively.It is obvious spatial aliasing is disappeared by using the random linear array regardless of linear motion or sinusoidal motion. However,there is another pronounced offset of DOA estimation when the source moves towards the end fire.

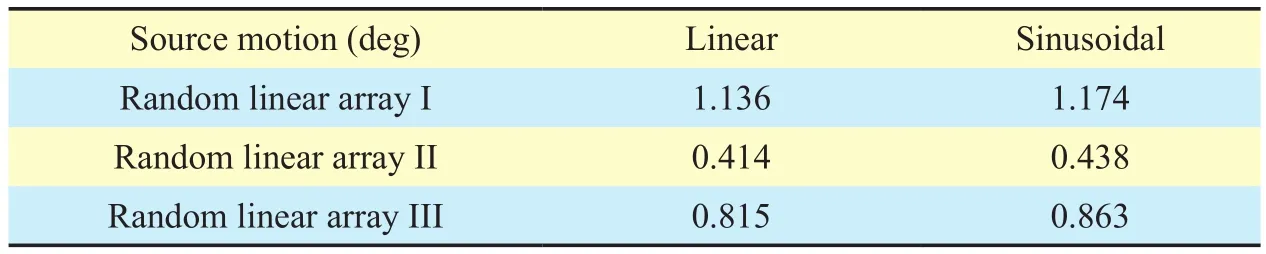
Table II. Maximum error comparison of DOA tracking for the single wideband sound source with linear motion and sinusoidal motion using three random linear array configurations in Fig. 2.

Figure 4(d) and figure 5(d) show the DOA tracking using the proposed method for the wideband sound source with linear and sinusoidal motion respectively. It is clear that the DOA tracking trajectories are consistent with trajectories of the true source. Figure 4(d) and figure 5(d) show the integrated error of DOA estimation is almost zero and the region of the end fire error shrinks as much as possible. The reason is that the prediction step of the proposed method provides a priori DOA knowledge of the current sources, so the weights of the particles surrounding the predicted locations are bigger than that of other position.We have made the experiment for tracking the single wideband sound source with linear motion with the Kalman filter method. The difference of the performance for tracking the single wideband sound source with linear motion with the Kalman filter method and the proposed method is not obvious, so we don’t show the results with the Kalman filter method in this part. We will analyze the performance of the Kalman filter method for tracking multiple wideband sound sources in chapter 4.2.2.

Table III shows maximum error comparison of DOA tracking for the source with linear and sinusoidal motions, and the positions of the maximum error are marked by the green points in the figures. It shows that the position of the maximum error is almost close to the endfire and the proposed method has the smallest maximum error.

Fig. 4. Single source with linear motion using random linear array at SNR of 40dB. DOA tracking using CS beamforming method for the narrowband source at frequencies of (a) 100Hz, (b) 250Hz and (c)340Hz. (d) DOA tracking using proposed method for the wideband sound source. “Wideband” means frequency spectra between 100Hz and 340Hz.

4.2.2 Multiple moving sources without intersecting

The simulated experiments are the DOA tracking for two moving sound sources without intersecting. Figs. 6(a) and 6(b) show the DOA tracking using CS beamforming method for two narrowband sound sources with linear motion at the frequencies of 100Hz and 340Hz respectively. Source1 moves from 0°to 90°, and source2 moves from −45°to 45°. It shows that the fluctuation error of the source1 is bigger than that of source2 at 100Hz and 340Hz between 60s～90s. The reason is that the direction of the source1 between 60s～90s are closer to the endfire region. Figs. 7(a),7(b) and 7(c) show the DOA tracking using CS beamforming method for two narrowband sound sources with sinusoidal motion at the frequencies of 100Hz, 250Hz and340Hz respectively. Source1 moves from 45°and source2 moves from −45°. The periodicity of the two sources motion is 40s. Similar to DOA tracking results of narrowband sources with linear motion, those of narrowband sources with sinusoidal motion also have large error at the end fire region.

Figs. 6(c) and 6(d) show the DOA tracking for two wideband sound sources with linearmotion using the Kalman filter method and the proposed method respectively. It shows that the fluctuation error of DOA tracking for the wideband sound sources using the proposed method is smaller than that using the Kalman filter method. Because the Kalman filter algorithm is not suitable for non-gaussian and nonlinear system, so we only apply it for wideband sound sources with linear motions. Figure 7(d) shows the DOA tracking results using the proposed method for wideband sound sources with sinusoidal motion. It is clear that the tracking trajectories are consistent with the true sources trajectories. Therefore, the proposed method can achieve a great performance in tracking multiple wideband sound sources with different motions.

Table III. Maximum error comparison of DOA estimation for the source with linear motion and sinusoidal motion(CS beamforming method for narrowband).

Fig. 5. Single source with sinusoidal motion using random linear array at SNR of 40dB. DOA tracking using CS beamforming method for the narrowband source at frequencies of (a) 100Hz, (b) 250Hz and (c) 340Hz. (d) DOA tracking using proposed method for the wideband sound source. “Wideband” means frequency spectra between 100Hz and 340Hz.

Under the hardware configuration of Pentium(R) Dual-Core E5800 CPU and 2 GB RAM, the computing time of the Kalman filter method for tracking two wideband sound sources with linear motions is 21.53 s, and the computing time of the proposed method is 300.55 s.

Table IV describes the maximum error and mean square error comparisons of DOA tracking with linear motion and sinusoidal motion.The maximum error of the proposed method is 1.83 degree which is smaller than that of the Kalman filter method 5.12 degree for the wideband source with linear motion. The maximum mean square error of the proposed method is 0.71 degree which is smaller than that of the Kalman filter method 1.85 degree .Comparison results show the proposed method has the smallest maximum error and mean square error. Although the computational complexity of the proposed method is higher than that of the Kalman filter method, the performance of the proposed method for tracking two wideband sound sources is better than that of the Kalman filter method.

Fig. 6. Two sources with linear motion using random linear array at SNR of 40dB. DOA tracking using CS beamforming method for narrowband sources at frequencies of (a) 100Hz, (b) 340Hz, (c) DOA tracking using the Kalman filter method for wideband sound sources, (d) DOA tracking using proposed method for wideband sound sources. “Wideband” means frequency spectra between 100Hz and 340Hz.

4.2.3 Multiple moving sources with intersecting

To analyze the resolution performance of the proposed algorithm, two wideband sound sources with linear motion intersecting at broadside and end fire are considered. Xenaki et al. [22] showed the two narrowband sources are resolved as one by the CS beamforming method when the two sources are close enough, and the angular resolution at endfire is much lower than that of broadside.

Figure 8 shows the angular resolution of CS beamforming method for two sources intersecting at broadside and endfire. It shows that the angular resolution is proportional tothe frequency, namely low frequency leads to low resolution. Figure 9 shows DOA tracking using the proposed method for two wideband sound sources intersecting at broadside and end fire respectively. The angular resolution is almost 2°for sources intersecting at broadside while up to 14°for sources intersecting at end fire. These two values are marked with dash line in figure 8. It can be seen that angular resolutions for the wideband sound sources are approximate to the resolution of the narrowband sound sources at high frequency,regardless of broadside or end fire. The reason is that the proposed method takes advantage of the high angular resolution of CS at high frequency and the prediction step imposes some inertia to the sources.

Table IV. Maximum error and mean square error comparison of DOA estimation for the sources with linear motion and sinusoidal motion (maximum error/mean square error, the Kalman filter method is simplified to KF and the particle filter method is simplified to PF for wideband sound source, ’--’ stands for blank, CS beamforming method for narrowband, KF and PF with CS method for wideband).

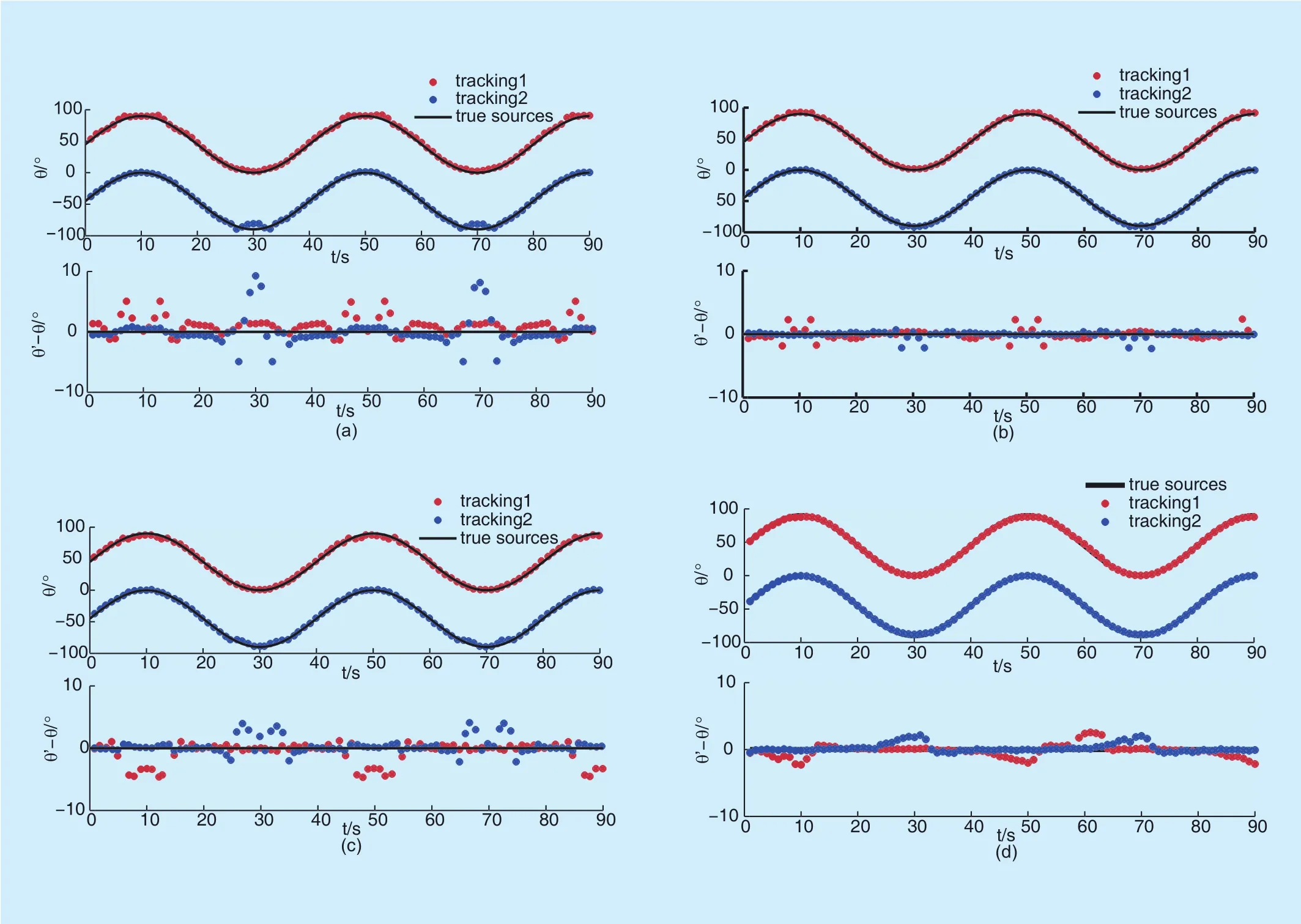
Fig. 7. Two sources with sinusoidal motion using random linear array at SNR of 40dB. DOA tracking using CS beamforming method for narrowband sources at frequencies of (a) 100Hz, (b) 250Hz and (c) 340Hz. (d) DOA tracking using proposed method for wideband sound sources. “Wideband” means frequency spectra between 100Hz and 340Hz.

Fig. 8. The angular resolution of CS beamforming method and the proposed method.

Fig. 9. DOA tracking using the proposed method for wideband sound sources intersecting at (a) broadside and (b) end fire. “Wideband” means frequency spectra between 100Hz and 340Hz.

V. CONCLUSION

In this paper, a particle filter based compressive sensing method is proposed for tracking moving wideband sources. We propose the following advantages using the proposed method for tracking moving wideband sound sources.(i) Spatial aliasing disappeared even by employing uniform linear array. The proposed method avoids the problem of false DOA estimation effectively and provides a good tracking performance. (ii) The offset at end fire decreases largely by using the proposed method, which can provide better performance of angular resolution. (iii) By combining CS with particle filter, and using the kernel density estimator as the likelihood function, the proposed method achieves great performance for tracking moving wideband sound sources.

ACKNOWLEDGEMENTS

This work was partially supported by the NFSC Grants 51375385 and 51675425,and Natural Science Basic Research Plan in Shaanxi Province of China Grants 2016JZ013.

[1] M.R AZIMI-SADJADI, A Pezeshki, N Roseveare,“Wideband DOA Estimation Algorithms for Multiple Moving Sources Using Unattended Acous-tic Sensors,” IEEE Transactions on Aerospace and Electronic Systems, vol. 44, no. 4, 2008, pp 1585-1599.

[2] H.G Yu, G.M Huang, J Gao, et al, “Approximate Maximum Likelihood Algorithm for Moving Source Localization Using TDOA and FDOA Measurements,” Chinese Journal of Aeronautics,vol. 25, no. 4, 2012, pp. 593-597.

[3] X.M Li, T Jiang, J.P An, et al, “Cooperative Communications Based on Rateless Network Coding in Distributed MIMO Systems,” IEEE Transactions on Wireless Communications, vol. 17, no. 3,2010, pp. 60-67.

[4] J Benesty, J Chen, Y Huang, “Conventional Beamforming Techniques,” Microphone Array Signal Processing, 2008, pp. 39-65.

[5] N Chu, J Picheral, A Mohammad-Djafari, et al, “A Robust Super-resolution Approach with Sparsity Constraint in Acoustic Imaging,” Applied Acoustics, vol. 76, 2014, pp. 197-208.

[6] P Simard, J Antoni, “Acoustic Source Identification: Experimenting the ℓ1 Minimization Approach,” Applied Acoustics, vol. 74, no. 7, 2013,pp. 974-986.

[7] J Benesty, J.D Chen, Y.T Huang, “A Generalized MVDR Spectrum,” IEEE Signal Processing Letters,vol. 12, no. 12, 2005, pp. 827-830.

[8] R Schmidt, “Multiple Emitter Location and Signal Parameter Estimation,” IEEE Transactions on Antennas and Propagation, vol. 34, no. 3, 1986,pp. 276-280.

[9] R Roy, T Kailath, “ESPRIT-estimation of Signal Parameters via Rotational Invariance Techniques,” IEEE Transactions on Acoustics, Speech,and Signal Processing, vol. 37, no. 7, 1989, pp.984-995.

[10] M.A Doron, A.J Weiss, H Messer, “Maximum-likelihood Direction Finding of Wide-band Sources,” IEEE Transactions on Signal Processing,vol. 41, no. 1, 1993, pp. 411.

[11] J Zhang, J.S Dai, Z.F Ye, “An Extended TOPS Algorithm Based on Incoherent Signal Subspace Method,” Signal Processing, vol. 90, no. 12,2010, pp. 3317-3324.

[12] H Wang, M Kaveh, “Coherent Signal-subspace Processing for the Detection and Estimation of Angles of Arrival of Multiple Wide-band Sources,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 33, no. 4, 1985, pp. 823-831.

[13] D.L Donoho, “Compressed Sensing,” IEEE Transactions on Information Theory, vol. 52, no. 4,2006, pp. 1289-1306.

[14] E.J Candes, “Compressive Sampling,” Proc. Proceedings of the International Congress of Mathematicians, Madrid, Spain, 2006, 3: pp. 1433-1452.

[15] N Wagner, Y.C Eldar, Z Friedman, “Compressed Beamforming in Ultrasound Imaging,” IEEE Transactions on Signal Processing, vol. 60, no. 9,2012, pp. 4643-4657.

[16] O Lorintiu, H Liebgott, M Alessandrini, et al,“Compressed Sensing Reconstruction of 3D Ultrasound Data Using Dictionary Learning and Line-wise Subsampling,” IEEE Transactions on Medical Imaging, vol. 34, no. 12, 2015, pp.2467-2477.

[17] J.G.C Clark, J.B Cain, “Error-correction coding for digital communications,” Springer Science &Business Media, 2013.

[18] L Anitori, A Maleki, M Otten, et al, “Design and Analysis of Compressed Sensing Radar Detectors,” IEEE Transactions on Signal Processing, vol.61, no. 4, 2013, pp. 813-827.

[19] H.J Yao, P.M Shearer, P Gerstoft, “Compressive Sensing of Frequency-dependent Seismic Radiation From Subduction Zone Megathrust Ruptures,” Proceedings of the National Academy of Sciences, vol. 110, no. 12, 2013, pp. 4512-4517.

[20] J.Z Huang, S.T Zhang, D Metaxas, “Efficient MR Image Reconstruction for Compressed MR Imaging,” Medical Image Analysis, vol. 15, no. 5,2011, pp. 670-679.

[21] H Xiong, Z.Y Chen, B.Y Yang, et al, “TDOA Localization Algorithm with Compensation of Clock Offset for Wireless Sensor Networks,” China Communications, vol. 12, no. 10, 2015, pp. 193-201.

[22] A Xenaki, P Gerstoft, K Mosegaard, “Compressive Beamforming,” The Journal of the Acoustical Society of America, vol. 136, no. 1, 2014, pp.260-271.

[23] H Zeng, Z Ahmad, J.W Zhou, et al, “DOA Estimation Algorithm Based on Adaptive Filtering in Spatial Domain,” China Communications, vol.13, no. 12, 2016, pp. 49-58.

[24] F.L Ning, J.G Wei, L.F Qiu, et al, “Three-dimensional Acoustic Imaging with Planar Microphone Arrays and Compressive Sensing,” Journal of Sound and Vibration, vol. 380, 2016, pp.112-128.

[25] D Malioutov, M Çetin, A.S Willsky, “A Sparse Signal Reconstruction Perspective for Source Localization with Sensor Arrays,” IEEE Transactions on Signal Processing, vol. 53, no. 8, 2005,pp. 3010-3022.

[26] G.F Edelmann, C.F Gaumond, “Beamforming Using Compressive Sensing,” The Journal of the Acoustical Society of America, vol. 130, no. 4,2011, pp. 232 - 237.

[27] P.T Boufounos, P Smaragdis, B Raj, “Joint Sparsity Models for Wideband Array Processing,”Proc. SPIE Optical Engineering+ Applications.International Society for Optics and Photonics,2011, pp. 81380K- 81380K-10.

[28] C Chang, R Ansari, “Kernel Particle Filter for Visual Tracking,” IEEE Signal Processing Letters, vol.12, no. 3, 2005, pp. 242-245.

[29] D.B Ward, E.A Lehmann, A.C Williamson, “Particle Filtering Algorithms for Tracking an Acoustic Source in a Reverberant Environment,” IEEE Transactions on Speech and Audio Processing,vol. 11, no. 6, 2003, pp. 826-836.

[30] J.M Valin, F Michaud, J Rouat, “Robust Localization and Tracking of Simultaneous Moving Sound Sources Using Beamforming and Particle Filtering,” Robotics and Autonomous Systems,vol. 55, no. 3, 2007, pp. 216-228.

[31] A Kijima, Y Hioka, N Hamada, “Tracking of Multiple Moving Sound Sources Using Particle Filter for Arbitrary Microphone Array Configurations,”Proc. Intelligent Signal Processing and Communications Systems (ISPACS), 2012 International Symposium on Taipei, Taiwan, 2012, pp. 108-113.

[32] S.S Chen, D.L Donoho, M.A Saunders, “Atomic Decomposition by Basis Pursuit,” SIAM Review,vol. 43, no. 1, 2001, pp. 129-159.

[33] E.J Candes, T Tao, “Decoding by Linear Programming,” IEEE Transactions on Information Theory, vol. 51, no. 12, 2005, pp. 4203-4215.

[34] T.T Cai, L Wang, “Orthogonal Matching Pursuit for Sparse Signal Recovery with Noise,” IEEE Transactions on Information Theory, vol. 57, no.7, 2011, pp. 4680- 4688.

[35] D Needell, J.A Tropp, “CoSaMP: Iterative Signal Recovery from Incomplete and Inaccurate Samples,” Applied and Computational Harmonic Analysis, vol. 26, no. 3, 2009, pp. 301-321.

[36] W Dai, O Milenkovic, “Subspace Pursuit for Compressive Sensing Signal Reconstruction,”IEEE Transactions on Information Theory, vol. 55,no. 5, 2009, pp. 2230-2249.

[37] T Blumensath, M.E Davies, “Normalized Iterative Hard Thresholding: Guaranteed Stability and Performance,” IEEE Journal of Selected Topics in Signal Processing, vol. 4, no. 2, 2010, pp. 298-309.

[38] J.A Tropp, A.C Gilbert, “Signal Recovery from Random Measurements via Orthogonal Matching Pursuit,” IEEE Transactions on Information Theory, vol. 53, no. 12, 2007, pp. 4655-4666.