Energy-Efficient Trajectory Planning for UAV-Aided Secure Communication
Qian Wang, Zhi Chen*, Hang Li
National Key Laboratory of Science and Technology on Communications, University of Electronic Science and Technology of China,Chengdu 611731, China
I. INTRODUCTION
Wireless communication is often vulnerable to signal interception due to the openness of the wireless transmission medium. As an information-theoretic approach for achieving perfect secrecy at the physical layer, physical layer security dose not rely on upper-layer encryptions in comparison to the traditional secretkey-based approach. This property makes physical layer security very attractive since key distribution and management may lead to security vulnerability in wireless systems. After Wyner’s seminal work [1], physical layer security has been studied for decades; notable works include the extension to Gaussian channels in [2], and the extension to broadcast channels with confidential messages in [3].
Thanks to the continuous development of autonomous or semi-autonomous vehicles,such as unmanned aerial vehicles (UAVs),the aerial communication platform has been recognized as a promising complement to the existing terrestrial wireless network. Relative projects are operated by many companies,e.g., Google [4] and Facebook [5]. The flexi-ble deployment of the UAV and the high line of sight (LOS) probability of the air-to-ground link make the UAV-aided aerial platform greatly applicable in many situations. A typical use case of UAV-aided wireless communications is UAV-aided ubiquitous coverage[6], where the UAV is employed to provide seamless coverage within the serving area. An example scenario is the rapid service recovery after terrestrial infrastructure damage. Another main application of UAV-aided wireless communications is UAV-aided mobile relaying[7], a technique adjusting the relay’s location adaptively based on the changing communication environment.
However, a variety of interesting challenges arise with the advent of UAV-aided wireless communications. In particular, to maintain the UAV aloft and support its mobility, a vast amount of energy is required, whereas the onboard energy is limited. Consequently, network operators should make great efforts to reduce the UAV’s energy consumption while satisfying the communication performance requirement. In [8], the authors acquired the propulsion energy consumption of the fixedwing UAV as a function of the UAV’s velocity and acceleration, based on which the communication throughput and the UAV’s propulsion energy consumption can be jointly considered.UAV-aided wireless communications offer new possibilities and opportunities for security enhancement. Recent works [9], [10] dealt with the secrecy rate maximization (SRM)problem in the UAV-aided network, where the high mobility of the UAV can be exploited to provide secrecy enhancement. However,this favorable prospect comes at the price of energy expenditure on UAV flying. This fact motivates us to jointly consider the secrecy performance and the UAV’s energy consumption.
In this paper, our research interest lies on the secrecy energy efficiency of the UAV-aided wireless communication. Specifically, we consider a three-node communication system including a legitimate receiver, an eavesdropper, and an aerial source aided by the fixedwing UAV, wherein we optimize the UAV’s trajectory in order to strike a tradeoff between the secrecy throughput and the UAV’s energy consumption. Given the fact that the radiation and signal processing energy consumption on the UAV is usually negligible compared to the UAV’s propulsion energy, the secrecy energy efficiency is defined as the secrecy information bits per unit propulsion energy consumption.Unfortunately, the resulting secrecy energy efficiency maximization (SEEM) problem is a large-scale nonconvex problem, and thus is intractable to solve.
The main contribution of this paper is to provide an efficient algorithm for the SEEM problem. Although the SEEM problem has an inherently complex problem structure, we show that sequential convex programming(SCP), together with Dinkelbach’s approach,can be applied to deal with it. Our proposed algorithm tackles the SEEM problem by solving convex problems in an iterative fashion.Besides the tractability, the proposed algorithm has a theoretically provable guarantee on the Karush-Kuhn-Tucker (KKT) point convergence of its solution. The numerical results validate the efficacy of our proposed algorithm in enhancing the system’s secrecy performance with acceptable energy consumption.
To gain new insights and provide benchmarks, we also study the unconstrained UAV trajectory for secrecy rate maximization(SRM), whose optimal solution is derived in closed form. Despite the impracticality of implementing the unconstrained SRM design in the fixed-wing UAV system, it is highly applicable in the rotary-wing UAV-employed case.
II. SYSTEM MODEL AND PROBLEM STATEMENT
Consider a wireless communication system consisting of an aerial source, a terrestrial destination (Bob), and a terrestrial eavesdropper(Eve), as schematically shown in figure 1. Unlike the conventional three-node wiretap channel, our system employs a fixed-wing UAV as an aerial source of sufficiently high mobility.The considered setup could be related to the military scenario, wherein the UAV acts as a relay connecting the command center with the front line. Also, the considered system could correspond to the service recovery scenario in cellular networks, after nature disaster destroys the backhaul links of the isolated base station.
Assume that the UAV flies at a constant altitude H within a finite time horizon T. In practice, H may be related to the minimum altitude where the UAV does not need frequent ascending and descending in order to avoid mountains or buildings. The time horizon T is discretized into N time slots, i.e., T=Nδt,where δtdenotes the slot length. The UAV’s location is assumed to be approximately invariable during each slot with δtchosen to be sufficiently small. Without loss of generality, a three-dimensional (3D) Cartesian coordinate system is considered, with Bob and Eve placed on the ground with coordinates (0,0,0) and (xE,0,0), respectively, while the UAV’s coordinate at slot n is represented as (x[ n ], y[ n], H), with x[ n] and y[ n] being the UAV’s x- and y-coordinates at slot n, respectively. In view of practicality, factors such as pre-mission/post-mission trajectories and launching/landing coordinates decide the initial and final UAV coordinates and velocities.Thus, the UAV in our scenario has predetermined initial and final coordinates represented as (x0, y0, H) and (xF, yF, H), respectively, and prearranged initial and final velocities being v0and vF, respectively. For ease of subsequent description, denote q[n ]≜[x[ n ],y[ n ]]T,as the UAV coordinate projected on the horizontal plane at slot n. In the same manner, letbe the projected coordinates of Eve, and the initial and final UAV locations, respectively. The slot length is sufficiently small, as mentioned before, so that the UAV’s acceleration vector can be viewed as approximately invariant during every slot. As a result, we have the following formulas, i.e.,
where v[n] and a[n] denote the UAV’s velocity and acceleration vectors at slot n, respectively.
Let hub[n ] and hue[n] represent the channel gains of the UAV-Bob link and the UAV-Eve link at the n th time slot, respectively. Analogous to [7], the air-to-ground channels follow the free-space path loss model:

with

and
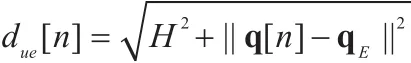
being the distances of the UAV-Bob link and the UAV-Eve link at slot n, respectively, and β0denoting the reference channel power at distance d0=1 meter.
Consider a constant transmit power P at the UAV, which could be relevant to the maximum value allowed by the authority regulations. Now, defineas the

Fig. 1. Secure wireless communication between a UAV-aided source and a terrestrial destination in the presence of a terrestrial eavesdropper.
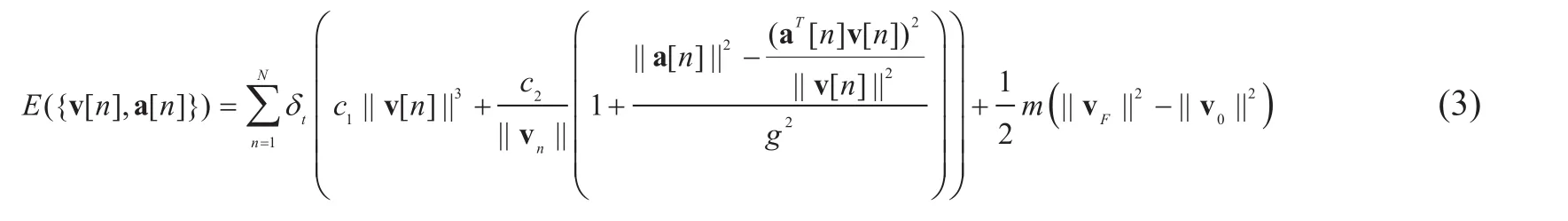
reference received signal-to-noise ratio (SNR),where δ2denotes the noise power. All channel coefficients are assumed to be available,including those for Eve. This is possible in scenarios where Eve is a network user, while it is not authorized as far as the message for Bob is concerned. Based on the above setup, an achievable secrecy rate can be written as [11]
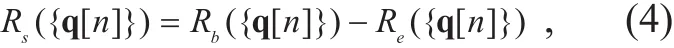
in which
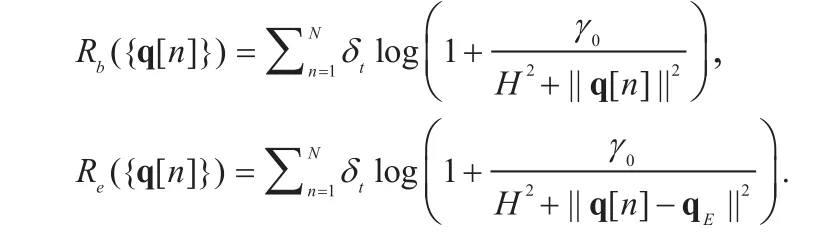
The total energy consumption of the UAV is made up of the communication-relevant energy and the propulsion energy. Due to the fact that the energy consumed on communication is extremely small compared to the propulsion energy [12], our work focuses on the latter,which is expressed as (3) (cf. [8]) at the bottom of page 53, where m is the mass of the UAV, g is the gravitational acceleration, and c1and c2are constant parameters depending on factors such as the aircraft’s weight and the air density. It should be mentioned that the rotary-wing UAV works in a different manner to the fixed-wing UAV [13]. Accordingly, the considered energy model (3) only applies to the fixed-wing case.
This work is interested in the design criterion of {q[ n]}, {a[ n]} and {v[ n]}, under a SEEM formulation, i.e.,

where E ({v[ n ],a[ n]}) and Rs({q[n]}) are given in (3) and (4), respectively,Vmaxand Vmindenote the maximum and minimum speeds, respectively, and amaxrepresents the maximum acceleration.
III. A TRACTABLE APPROACH TO THE SEEM PROBLEM
The nonconvexity of Rs({q[n ]}), E ({v[ n ],a[ n]}),and (5f) suggests that the SEEM problem (5)is a nonconvex problem. Accordingly, our aim is to seek a suboptimal solution for SEEM.We begin by considering an upper bound of E ({v[ n ],a[ n ]}), i.e.,
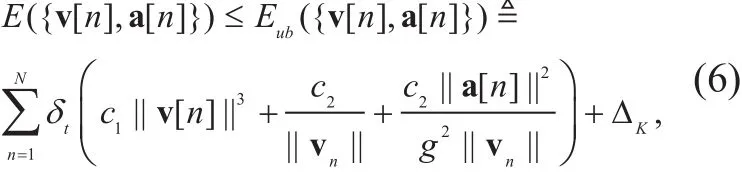
whereis a constant since the initial and final UAV velocities are predetermined in (5c). Then, the energy efficiencyis lower-bounded by, based upon which we obtain an approximated SEEM problem, i.e.,

In the sequel, we will propose an iterative algorithm, by invoking sequential convex programming (SCP), to search for a Karush-Kuhn-Tucker (KKT) point of the approximated SEEM problem (7). Its basic idea is to successively construct subproblems at successive iteration points.
To simplify the objective, problem (7) is equivalently reformulated as
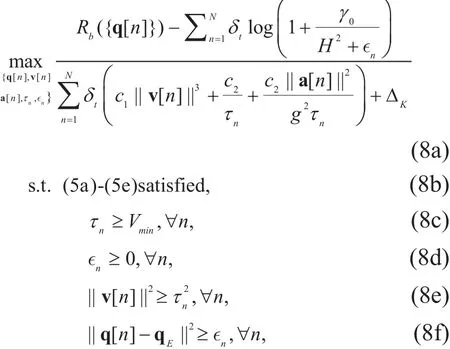
where {τn,∈n} are slack variables. It can be verified by contradiction that the optimal solution of problem (8) must satisfy all constraints in (8e) and (8f) with equality, thus problem (8)is an equivalent transformation of problem (7).
Before proceeding further, we define η(v[n ])=||v[n ]||2and ξ(q[ n ])=| |q[ n] − qE||2for notational convenience and present the following lemma.
L e m m a 1: F o r a n y {q[ n]} a n d{v[ n]}, Rb({q[n]}), η(v[ n]), and ξ(q[ n]) can be lower-bounded by

and

respectively, where {q0[n ]} and {v0[n ]} can be any feasible UAV trajectory and UAV speeds,and

Proof: See Appendix VII-A for a detailed proof.
Invoking Lemma 1, we reformulate problem (8) by approximating Rb({q[n ]}),||v[ n]||2,and ||q[n] −qE||2in (8a), (8e), and (8f) with their lower boundsand ξlb(q[ n]), respectively. The resulting approximated SEEM problem is written as
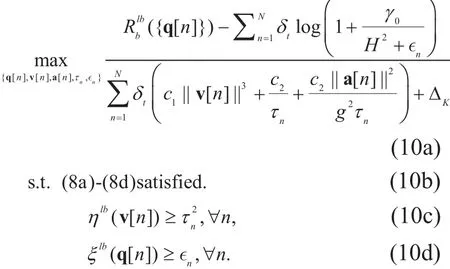
For the convenience of subsequent description, let us denote the numerator and denominator in the objective function of problem (10)as f({q[ n],∈n}) and g ({v [n ],a[ n],τn}), respectively.
One can easily obtain the fact that−f({q[ n],∈n}), g ({v[ n ],a[ n],τn}), and all the constraints in (10) are convex. Thus, problem(10) can be conveniently solved by employing fractional programming methods, e.g., the standard Dinkelbach’s algorithm [14]. Dinkelbach’s procedure can be deemed as a method to identify a root of the equation F(λ)=0,wherein F()λ is given by

With a given parameter λ, problem (11) is convex so that its optimal solution can be obtained by exploiting a general purpose convex optimization technique, like the interior-point method [15]. The upshot of the Dinkelbach’s procedure is that one can optimally solve problem (10) by iteratively solving problem(11) with updating λ.
Our proposed approach for the SEEM problem is summarized in Algorithm 1, which has two levels. The outer level (level 1) is related to the iteration of the SCP algorithm. The inner level (level 2) corresponds to the iteration of the Dinkelbach’s method. One can see that the basic merit of the proposed algorithm lies in the tractability, which only requires solving convex optimization problems. As an additional merit, Algorithm 1 has theoretically provable convergence:
Theorem 1: Algorithm 1 is guaranteed to converge to a KKT point of the approximated SEEM problem (7).
Proof: The proof of Theorem 1 is relegated to Appendix VII-B.

?
IV. SECRECY RATE MAXIMIZATION WITH UNCONSTRAINED TRAJECTORY
In this section, we investigate the secrecy rate maximization (SRM) problem, without considering the constraints on the UAV trajectory,i.e., (5b)-(5f), so as to draw new insights.
In the absence of constraints on the UAV trajectory, one can immediately derive the fact that the UAV trajectory for SRM should be a fixed point (xs,ys,H), i.e., the location corresponding to the best secure transmission channel. Now, we are interested in designingfor SRM, i.e.,

A major challenge in solving problem (12)lies in the coupling of xsand ys. Thankfully,we can prove that the optimal ysshould be 0(cf. Lemma 3). As a benefit of this, the optimal solution of problem (12) can be obtained in closed form, which is presented in the following lemma.
Lemma 2: The x- and y-coordinates of the optimal UAV location for SRM are given by

whereand
Proof: See Appendix VII-C for a detailed proof.
It should be pointed out that we ignore the case xE=0, due to the fact that Bob and Eve cannot be located at the same place in view of practicality.
Remark 1: It is impossible for a fixed-wing UAV to stay stationary in the air, thus the SRM design is evidently energy inefficient. Nevertheless, the SRM design is highly applicable in situations where the UAV has rotary-wings such that the energy consumption for hovering at a stationary point is endurable, especially with a short service time and adequate power supply from battery or wireless power transfer.
V. NUMERICAL RESULTS
In this section, numerical results are given to show the performance of the proposed design.Overall simulation settings are as follows:The communication bandwidth and the noise power spectrum density are B=1MHz and N0= −170dBm/Hz, respectively. The UAV’s transmission power is P=10dBm, and the reference channel power is β0= −50dB. Accordingly, the reference SNR at distance d0=1 m is γ0=70dB. Moreover, we set c1=9.26× 10−4and c2=2250. The flying altitude of the UAV is fixed at H=100 m and the UAV’s service time is set to be T=200 s. The x-coordinate of Eve is assumed to be xE=−200 m.
5.1 Case 1: unconstrained trajectory design
In this case, we consider the trajectory optimization problem in the absence of constraints (5b)-(5f), i.e., the UAV is assumed to have no restrictions including speed and acceleration limits, and predetermined initial and final coordinates and velocities. Based on our setup, the optimal UAV trajectory for SRM should be hovering at the fixed location(41.1415m,0,100m), which we will refer to as the SRM hovering point in the remaining part of this paper. The unconstrained SEEM design can be derived through utilizing a similar SCP approach as the one presented in Algorithm 1.In figure 2 we plot the obtained unconstrained UAV trajectory projected onto the horizontal plane for SEEM. As one can see, the UAV flies around the SRM hovering point to achieve high-security communication, while following a trajectory made up of “8”-shape paths to maintain acceptable power consumption.
5.2 Case 2: constrained trajectory design
In this case, the trajectory optimization problem with constraints is considered.
We set the initial and final locations to be q0=[0,1000]Tand qF=[1000,0]T, respectively. The initial and final velocities are set as v0=vF=30(qF− q0)/||qF−q0||. Next, let the maximum and minimum UAV speeds be Vmax=100 m/s and Vmin=3 m/s, respectively.The maximum acceleration speed is assumed to be amax=5 m/s2. In figure 3 we plot the constrained UAV trajectory projected onto the horizontal plane for SEEM and that for SRM.Here, we should mention that the constrained UAV trajectory for SRM can be obtained by invoking a similar SCP approach as that in Algorithm 1. From the figure, we can see that for both SEEM and SRM, the UAV flies from the initial location to places around the SRM hovering point to achieve good secrecy transmission. In contrast to the SEEM design, the SRM design allows drastic changes in the UAV’s heading direction, which are energy-consuming, in exchange of high-security communication. As expected, the SEEM design expresses more tolerance towards inferior channels so as to strike a tradeoff between the secure transmission and the power consumption.
Table I provides the system performance for SEEM and SRM with constrained and unconstrained trajectory designs. As a benchmark, the performance of the heuristic straight flight from q0to qFwith fixed velocity is also presented in table I. From the table, one can easily see that compared to the heuristic straight flight, the SEEM design obtained by our proposed algorithm experiences lower power consumption and higher secrecy rate at the same time, even with practical constraints.Table I also shows that compared to the SRM design, the SEEM design could strike a sig-nificantly better secrecy rate-power consumption tradeoff. These observations demonstrate that our proposed algorithm can improve the secrecy energy efficiency significantly.

Fig. 2. Unconstrained UAV trajectory for SEEM. The triangle, diamond, and star represent Bob, Eve and the SRM hovering point, respectively.

Fig. 3. Constrained UAV trajectories for SEEM and SRM, respectively. The diamond, square, circle, and star denote Eve, initial and final locations, and the SRM hovering point, respectively.

Table I. performance comparison for various designs.
VI. CONCLUSION
In this paper, we investigated the SEEM problem in a UAV-aided network. Specifically, we optimized the UAV trajectory to maximize the secrecy information bits per unit propulsion energy consumption. The SEEM problem is challenging due to its inherently complex structure. As a compromise, an efficient iterative algorithm based on SCP and Dinkelbach’s method was proposed to seek a suboptimal solution for SEEM. The proposed algorithm is proved to have KKT point convergence. Additionally, the optimal unconstrained trajectory for SRM is derived in closed form, which is energy inefficient with the fixed-wing UAV,while applicable with the rotary-wing UAV.
VII. APPENDIX
7.1 The proof of Lemma 1
One can easily verify thatwith some constant γ> 0 and A, is convex for w>−A. Thus, the first-order Taylor series expansion of h( w) at any feasible point w0> −A is a lower bound of h( w), i.e.,
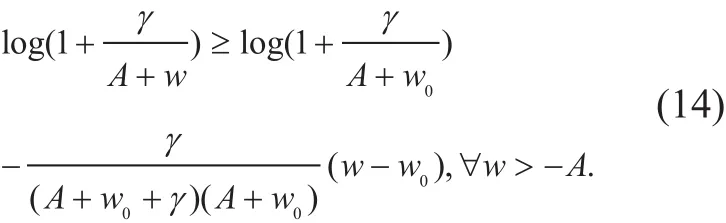
(9a) follows from (14) by letting γ=γ0,A=H2,w0=||q0[n ]||2, and w=||q[n]||2. (9b) and (9c) can be obtained in a similar manner: since both||v[ n]||2and ||q[n] −qE||2are convex functions,their respective lower bounds ηlb(v[ n]) and ξlb(q[ n]) can be derived by exploiting first-order Taylor series expansions.
7.2 The proof of Theorem 1
To begin with, one can obtain the gradients of Rb({q[n ]}) and Rblb({q[n ]}) with respect to q[n],which are:

and
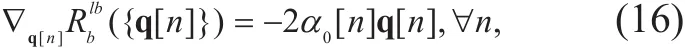
respectively. The gradients of η(v[ n]) and ηlb(v[ n]) with regard to v[n] can be derived as

and

respectively. Moreover, the gradients of ξ(q[ n]) and ξlb(q[ n]) with respect to q[n] are

and

respectively. It is easy to see that with q[n] = q0[n] and v[n ] = v0[n ],∀ n,we have the following equations:

and

In addition, one can easily obtain the fact that when q[n]= q0[n] and v[n ] = v0[n ],∀ n,all the inequalities in (9a)-(9c) hold with equality.Based on the above facts, Theorem 1 can be immediately derived according to [16, Proposition 3].
7.3 The proof of Lemma 2
To acquire the optimal solution of (12), denoted by, we will need the following lemma:
Lemma 3: The y-coordinate of the optimal UAV location for SRM, i.e.,, should be zero.
Proof: To begin with, we have


where

and

Suppose that a1≥ a4holds at point. One can easily find another solutionsatisfyingand attain a larger objective, which is a contradiction. This concludes that a4>a1.Due to the fact that

and
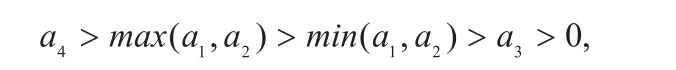
it is easy to obtain that a1a2> a3a4. Now, we have
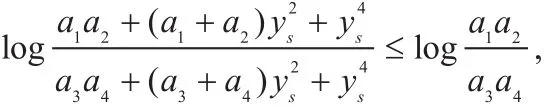
wherein the equality holds iff ys=0. This thus completes the proof.
According to Lemma 3, problem (12) can be equally written as

w h e r eBy setting the first-order derivative of U( xs)to zero, the closed-form optimal solution of problem (12), as shown in Lemma 2, can be derived.
ACKNOWLEDGMENT
This work was supported in part by the National Natural Science Foundation of China under Grant 61631004 and 61571089.
[1] A. D. Wyner, “The wire-tap channel,” Bell Syst.Tech. J., vol. 54, no. 8, Oct. 1975, pp. 1355–1387.
[2] S. Leung-Yan-Cheong and M. Hellman, “The Gaussian wire-tap chan- nel,” IEEE Trans. Inf.Theory, vol. 24, no. 4, Jul. 1978, pp. 451–456.
[3] I. Csiszár and J. Körner, “Broadcast channels with confidential mes- sages,” IEEE Trans. Inf. Theory,vol. 24, no. 3, May 1978, pp. 339–348.
[4] S. Katikala, “Google project loon,” InSight: Rivier Academic Journal, vol. 10, no. 2, 2014.
[5] Y. Zeng and R. Zhang and T. J. Lim, “Connecting the world from the sky,” Facebook, Technical Report, 2014.
[6] Y. Zeng, R. Zhang, and T. J. Lim, “Wireless communications with un- manned aerial vehicles:Opportunities and challenges,” IEEE Commun.Mag., vol. 54, no. 5, May 2016, pp. 36–42.
[7] Y. Zeng and R. Zhang and T. J. Lim, “Throughput maximization for UAV-enabled mobile relaying systems,” IEEE Trans. Commun., vol. 64, no. 12,pp. 4983–4996, Dec. 2016.
[8] Y. Zeng and R. Zhang, “Energy-efficient UAV communication with trajectory optimization,”IEEE Trans. Wireless Commun., vol. 16, no. 6,Jun. 2017, pp. 3747-3760.
[9] Q. Wang, Z. Chen, W. Mei, and J. Fang, “Improving physical layer security using UAV-enabled mobile relaying,” IEEE Wireless Commun. Lett.,vol. 6, no. 3, Jun. 2017, pp. 310–313.
[10] G. Zhang, Q. Wu, M. Cui, and R. Zhang, “Securing UAV communi- cations via trajectory optimization,” Proc. IEEE Global Communications Conference, Singapore, Dec. 2017, pp. 1–6.
[11] T. Liu and S. Shamai (Shitz), “A note on the secrecy capacity of the multi-antenna wiretap channel,” IEEE Trans. Inf. Theory, vol. 55, no. 6,Jun. 2009, pp. 2547–2553.
[12] C. D. Franco and G. Buttazzo, “Energy-aware coverage path planning of UAVs,” Proc. IEEE Int.Conf. Auto. Robot Syst. Compet., Apr. 2015, pp.111–117.
[13] A. Filippone, Flight Performance of Fixed and Rotary Wing Aircraft. Washington, DC: USA:AIAA, 2006.
[14] J.-P. Crouzeix and J. A. Ferland, “Algorithms for generalized fractional programming,” Math.Programm., vol. 52, no. 1, 1991, pp. 191–207.
[15] S. Boyd, EE364b convex optimization II. Course Notes, available online at http://www.stanford.edu/class/ee364b.
[16] A. Zappone, E. Bjornson, L. Sanguinetti, and E. Jorswieck, “Achieving global optimality for energy efficiency maximization in wireless networks,” Available online at https://arxiv.org/abs/1602.02923.
- China Communications的其它文章
- Geometric Mean Decomposition Based Hybrid Precoding for Millimeter-Wave Massive MIMO
- Outage Performance of Non-Orthogonal Multiple Access Based Unmanned Aerial Vehicles Satellite Networks
- Outage Probability Minimization for Low-Altitude UAV-Enabled Full-Duplex Mobile Relaying Systems
- Optimal Deployment Density for Maximum Coverage of Drone Small Cells
- Energy Efficient Multi-Antenna UAV-Enabled Mobile Relay
- An Enhanced Direct Anonymous Attestation Scheme with Mutual Authentication for Network-Connected UAV Communication Systems

