Guaranteed Rendezvous Algorithms for Cognitive Radio Networks

Li Gou, Xiaohua Xu, Chongqing Zhang, Min Song,＊

1 Department of Computer Science, Michigan Technological University, Houghton, Michigan 49931, USA

2 Department of Computer Science, Kennesaw State University, Marietta, GA 30060, USA

3 College of Computer Science & Engineering, Shandong University of Science and Technology, Shandong 266590, China

I. INTRODUCTION

With the increase of spectrum demanding on various services and applications, the spectrum scarcity remains a critical problem for wireless communications. Dynamic Spectrum Access (DSA) was proposed with cognitive radio networks (CRNs). With DSA, secondary users (SUs) can dynamically detect and access the idle licensed spectrum assigned to primary users (PUs). However, the dynamics of PUs’activities force SUs to adapt to the variations in channel availability. Thus, finding common available channels among the SUs on demand is critical before communications. The process that the SUs establish a communication link on a common channel is called rendezvous.

Common control channel based rendezvous schemes [1] use the common control channel to help the nodes establish the communication link. But the high traf fic required on the common control channel causes network congestion and high overload cost. To overcome these issues, blind rendezvous algorithms based on channel hopping (CH)were then proposed [2], [3]. Jump-stay rendezvous algorithms considering symmetric model are proposed in [4], [5]. They achieve guaranteed rendezvous by constructing CH sequence combining periods of jump-pattern and stay-pattern. Both the sequence based rendezvous algorithm proposed in [6] and the rendezvous algorithms considering synchro-nization proposed in [3] can only be applied to symmetric model. The probability based CH algorithm proposed in [7] depends on the preassigned order among the nodes in the network to further assign roles to each node.The asynchronous quorum based rendezvous algorithm proposed in [8] can only reach rendezvous on the two of the available channels,and its asynchronous Latin square based algorithm can only be applied in symmetric model.The heterogeneous hopping (HH) algorithm in[2] assumes that the available channels of each node are consecutive. As observed in [9], the moving traversing pointers (MTP) algorithm proposed in [10] is not highly efficient if the spectrum is fully available. The disjoint set cover based rendezvous (DSCR) algorithm in[9] assumes that the same channel label (or index) of a channel is used between a pair of nodes. In other words, they do not consider the oblivious setting for channel labeling. Here,the definition of oblivious channel labeling is available in [11]. There are also several existing work on multi-radio rendezvous algorithm design [12]–[18]. In [18], Lin et.al. proposed a channel-hopping scheme to preserve network connectivity while the scheme cannot guarantee rendezvous. In [14], Yu et.al. assumed that channels are fully available and proposed a rendezvous algorithm called role-based parallel sequence (RPS). In [13], Paul et.al.proposed an Enhanced Adaptive Rendezvous(EAR) with no theoretical upper bound on the time to rendezvous. In [15], Yu et.al. proposed an adjustable multi-radio rendezvous algorithm (AMPP) which constructs the CH sequence based on local channels. The AMPP algorithm can adjust its best performance on either the maximum time to rendezvous or the average time to rendezvous. A deterministic multi-radio rendezvous scheme called multigrid-quorum channel hopping is proposed in[16]. In [17], Yang et.al. proposed a multiradio-sun flower-set-based rendezvous algorithm.In [12], Li et.al. provided an lower bound on the time to rendezvous and a family of algorithms under different cases.

This paper proposes a rendezvous algorithm named cycle length based rendezvous(CLR) algorithm for singleradio CRNs.

However, there is still a lack of work that solves the rendezvous problem under heterogeneous and asynchronous model with oblivious channel labeling. In this paper, we first propose an oblivious guaranteed rendezvous algorithm called cycle length based rendezvous (CLR) algorithm for heterogeneous CRN under asynchronous situation. There is a possibility of unguaranteed rendezvous(deadlock situation) using the random CH sequence when the cycle lengths between the two nodes (Tiand Tj) are not coprime. So in CLR algorithm, the threshold Tmax, the length of the maximal possible rendezvous period between the two nodes i and j is used to detect the deadlock situation. Once the deadlock situation is detected, the bit-by-bit cycle length change is independently applied on each node to guarantee rendezvous.

We then design a rotation and cycle length based rendezvous (MR-RCLR) algorithm for two-radio CRN, where two radios are assigned to each node. In MR-RCLR algorithm, node i firstly generate the initial CH sequencewith cycle length, then the two radios of node i apply different number of rotations oncycle by cycle and attempt rendezvous with the radios of the other node. The rendezvous between node i and node j is always guaranteed within one rendezvous period.This is because either Tiand Tjare coprime or the number of rotations between the radios of the two nodes are different. In addition,we resolve the channel collision between the two radios of each node during the hopping process. The MR-RCLR algorithm attainstime slots, which is better than the algorithm assigning two different cycle lengths to the two radios proposed in [12].The contribution of this paper is summarized as follows:

• The CLR algorithm applies deadlock checking using the threshold Tmaxand independently oscillates the cycle lengths betweenbit by bit on the node ID to guarantee rendezvous within the upper bound. The CLR algorithm is proved to be guaranteed under all the possible time skew δ∈[0,Ti) (asynchronous system) via both theoretical analysis and simulation study.

• The MR-RCLR algorithm is always guaranteed withintime slots. The collisions between the two radios of the same node are resolved during the hopping process.

• The performance of both CLR and MRRCLR algorithms is totally independent with the channel IDs, and channel loads are smoothly distributed on each channel.

The rest of this paper is organized as follows. The system model and problem formulation are provided in Section II. Section III presents the details of the proposed CLR algorithm and the theoretical analysis. The MR-RCLR algorithm including the collision resolution is presented in Section IV. The simulation results are presented in Section V. We conclude in Section VI.

II. SYSTEM MODEL AND PROBLEM FORMULATION

In this section, we present the system model and problem formulation. Table 1 summarizes the notations used.

2.1 System model

We consider a CRN of multiple nodes. Each node has a unique ID, denoted as IDi. The binary representation of the IDi, called binary ID of node i, is defined aswhereis the k-th bit of Biandis the width or number of bits of Bi. In addition, the bit sequence of Biis in the order of least significant to most significant bit. For the two nodes i and j in the CRN,BiBj, so there is at least one different bit in their binary IDs.

In this paper, we only discuss the two-node scenario. Assume that all the radios in the CRN have the same maximal sensing capability,denoted as C. Letbe the set of channels available to node i, and |Ci|is the total number of available channels, so|Ci|＜ C . Assume that the channels available to each node cause no interference to any PU.In this paper, we consider heterogeneous model, thus Ciand Cjcan be different in both length and range of the available channels, and we have

In the random CH scheme, node i independently generates random CH sequence with a prime number as cycle length Ti. To attempt rendezvous, the radio of each node hops on one channel at each time slot. The rendezvous is reached when the radios of the two nodes hop on the same channel at the same time slot.The number of time slots required to rendezvous is defined as Time to Rendezvous (TTR).The Maximal Time to Rendezvous (MTTR) is the TTR in the worst case, and the Expected Time to Rendezvous (ETTR) is the average TTR over different cases. The rendezvous period is defined as a period where the hopping and alignment between the CH sequences of the two nodes i and j repeat. Let the length of the rendezvous period be T, so T=k* Ti,where k is the number of CH sequence cycles in one rendezvous period of node i. For the two nodes i and j, it is possible that there is no rendezvous between them by hopping on therandom CH sequences when Ti= Tj. So the deadlock in rendezvous is defined as the situation where the two nodes can not rendezvous with each other forever. Thus, in this paper we decides deadlock situation by a certain amount of time, the threshold Tmax, which is the length of the maximal possible rendezvous period between the two nodes.

Table I. Notation.

2.2 Problem formulation

We consider an asynchronous system in this paper. The time is slotted with the same and fixed length. The time skew is defined as the number of time slots the CH sequences of the two nodes misaligned, so any time skew is possible in the asynchronous system. Let δ be the time skew between the CH sequences of the two nodes i and j, δ≥0. Without loss of generality, we assume node i always starts hopping earlier than node j if δ＞0. That is, if node i starts hopping at time slot t, then node j starts at t+δ, and δ is in the range:δ∈[0,Ti).

Let the CH sequence of node i bewhererepresents the channel hopped at time slot t, and Tiis a prime number representing the cycle length of the CH sequence.The CH sequence can also be defined in cycles as:whereis the x-th cycle. For each cycle of the CH sequence,wheredenotes the y-th channel at the x-th cycle. Thus the time slot when radio i hopes on channel

The rendezvous problem of finding the time slot the rendezvous is reached between nodes i and j can be defined as follows:

where t is the TTR for node i, and t−δ for node j. Then the maximal time slots required for rendezvous between the two nodes can be defined as MTTR=max∀δt .

III. SINGLE-RADIO CYCLE LENGTH BASED RENDEZVOUS ALGORITHM

3.1 The CLR algorithm

The CH sequence of the proposed CLR algorithm is constructed based on cycle length.For each node i, we define two cycle lengths as follows: i), the minimum prime number no less than |Ci|. ii), the smallest prime number greater than. Based on the two possible cycle lengths, two CH sequences is constructed for each node in cycle as following:

where czj, j ∈ {1,2,… } is an arbitrary channel in Ci. For fairness, each channel should appear no more than twice in each of the CH sequence. At each cycle x, node i will choose one of the two CH sequences based on its cycle length. If

We consider two cases based on based on the cycle length of each node when design CLR algorithm: i) Tiand Tjare coprime, i.e.,Ti≠ Tj, in which the rendezvous is guaranteed at the first rendezvous period within Ti· Tj+δ time slots. ii) Tiand Tjare not coprime, i.e.,Ti= Tj, where rendezvous may not be reached within the first rendezvous period as well as the future rendezvous periods. For the second case, a threshold Tmax, which is the length of the maximum possible rendezvous period between the two nodes wishing to rendezvous,is used to check the deadlock situation. We consider two cases for the definition of the threshold Tmax: i)used at the first deadlock checking, where Tcis the maximal possible cycle length of the nodes in the same CRN, i.e., Ti≠ Tc, for node i. Tcis calculated by the minimum prime number no less than C(C is the maximal channel sensing ability of all the radios in the CRN). ii)used for the future deadlock checking. For the first deadlock checking occurs at(the rendezvous between nodes i and j is not reached after hoppingtime slots), the equality between Tiand Tjwill be learned by both the two nodes attempting rendezvous. Then each node will independently update its cycle length betweenandbased on the first bit of their binary IDs.For the future deadlock checking occurs ateach node will independently update its cycle length based on the other bits of their binary IDs until rendezvous is reached.

For nodes i and j, based on the definition of the binary ID, ∃k, k ∈{1,2,…, min{ Wi, Wj}+ 1}, such that,. Let l∈{1,2,…, min{ W, W}+ 1},ijthe following two situations exist during the deadlock checking on bit: i) current checking bit=0, node i sets its cycle length to Ti=; and ii)=1, node i sets its cycle length to Ti=. Then node i hops on the CH sequence generated by Eq. 2 with the new cycle length. If the rendezvous is not reached withintime slots, deadlock situation occurs, node i will check the next bit. Otherwise, the rendezvous will be guaranteed during this rendezvous periodIt should be noted that if the rendezvous is not reached until all the bits in Bjhas been checked, then=0 when l′＞, if W ＞ W; vice versa.ij

Figure 1 shows the rendezvous process described above. When t＜Ti*Tc, node i hops on its CH sequence with Ti=until the rendezvous is reached (Figure 1(a)), otherwise,the deadlock situation will be encountered( first period of Figure 1(b)). When t≥Ti* Tc,the two nodes will continue hopping on its CH sequence and independently conduct deadlock checking bit by bit on its binary ID and oscillate its cycle length betweenand.As long as the current checking bits between nodes i and j are different, the cycle lengths between them will also be different, and the rendezvous can be reached in the following rendezvous period, as shown in the third period of Figure 1(b).

Fig. 1. Illustration of the rendezvous process when and (a) When, the rendezvous is guaranteed within time slots. (b) When, deadlock situation is detected at time slot t=, and each node then oscillate its cycle length between independently at each following rendezvous round based on the binary ID. Rendezvous is reached at the last round as long as where

In Algorithm 1, the function toBinary(IDi)is used to convert the IDito binary format.The function minPrime(.) will return the next prime number greater than the parameter. In line 2, the two cycle lengths are initialized,and the two CH sequences for node i are generated in line 3. Theandare initially assigned to node i in line 4. For the deadlock checking process from line 7 to 23, lines 8-13 are the checking on the first bit, while lines 14-21 are checking on the other bits. The rendezvous is attempted on each channel of the CH sequence in lines 24-30.

We make a note that the unique ID property for assigning different roles to a pair of nodes has been explored in previous work such as[19], [20].

3.2 Performance analysis

Here we will analyze the performance of Algorithm 1 by considering all the possible time skew δ∈[0,Ti) between the CH sequences of nodes i and j.

?

Lemma 1For nodes i and j, with δ=0 and Ti≠ Tj, let the length of the rendezvous period be T=Ti*Tj. For any two CH sequences of nodes i and j, if no rendezvous can be reached within T time slots, then there is no guaranteed rendezvous between the two nodes(deadlock situation). Otherwise MTTR=T.

Proof:We prove the lemma 1 by contradiction. Assume nodes i and j rendezvous at time slot T+k after the first rendezvous round,0≤k＜T. Within a rendezvous round (T time slots), node i hops for r=T/ Ticycles, and node j for s=T/ Tjcycles. Thus, the last hop by nodes i and j at each rendezvous round,and, are always aligned with each other, where m is the number of rendezvous rounds. So at time slot t = mrTi=msTj,both nodes i and j repeat the hopping of the former rendezvous round with same CH sequence and same alignment. Therefore, if no rendezvous is reached in the first cycle, there is no rendezvous in future cycles. This is a contradiction with the assumption.

Theorem 1The rendezvous between nodes i and j is guaranteed intime slots, considering all the possible time skew δ∈[0.Ti) between their CH sequences.

Proof:There are four cases:

Case 1Ti≠ Tj,δ=0, proved by Theorem 6 of [2], and MTTR=Ti*Tj. This paper mainly focuses on the other three cases.

Case 2Ti≠ Tj,δ＞0, where node i starts δ time slots earlier than node j. Assume that node i starts hopping at time slot t=0,so node j starts hopping at time slot δ. Letbe another CH sequence for node i. It is clear thatis a clockwise rotation of the original CH sequence of node i :by δ time slots. That is:

So the rendezvous between Siand Sjwith δ time skew is equivalent with the rendezvous betweenand Sjwith zero time skew.Thus this case is equivalent to the case that both nodes i and j start hopping at time slot t=δ with no time skew, which is exactly the case 1. So the rendezvous of this case is still guaranteed, and MTTR=Ti* Tj+δ.

Case 3Ti= Tj,δ=0. The worst case is when the two nodes can not rendezvous within the first rendezvous period (length of T=Ti=Tjtime slots) and the deadlock checking occurs. For the deadlock checking process starting at t=Ti*Tc, the worst case is whenand(assuming Wi＞ Wj). In this case, the deadlock checking process will repeat for Wjtimes, and the rendezvous can only be reached on the next rendezvous period. Based on Algorithm 1, both the deadlock checking process on each of the Wjbits and success rendezvous process during next period taketime slots. Thus,

Case 4Ti= Tj,δ＞ 0. Based on cases 2 and 3, it’s easy to find that the rendezvous of this case is still guaranteed, and

IV. MULTI-RADIO ROTATION BASED RENDEZVOUS ALGORITHM

4.1 Algorithm design

In this section, multiple radios are introduced to reduce the rendezvous time. Considering the cost on setting up radios, the algorithm we designed only requires two radios. Letandare the two radios of node i. In the proposed MR-RCLR algorithm, each nodefirstly generates its initial CH sequencewith cycle lengthbased on Eq. 2, then the two radios of the node independently apply different number of rotations on. Let the number of rotation made by radiois,and that of radioisandare randomly selected from the set [1,) by radioandrespectively, and＜. The CH sequence of node i based onwithrotations is defined as follows:

When the cycle length between the two nodes are coprime, the rendezvous is always guaranteed no matter their number of rotations are different or not [2]. It is also proved in Lemma 2 of [4] that rendezvous between the two nodes is guaranteed as long as their number of rotations on the CH sequence are different if their cycle length are the same.The MTTR of both the two cases areThere are following possible situations about the rendezvous between the two nodes i and j: i) When their cycle length are coprime,rendezvous can be reached between any pair out of the four pairs of radios between the two nodes. ii) Whenall the four radios choose different number of rotations, the rendezvous can be reached between any pair of radios. iii) Whenradios of node i select same number of rotations as nodethe rendezvous can be reached between at least two of the fours pairs of radios of the two nodes.

Asynchronous ScenarioFor the multi-radio scenario, the two radios of each node can start hopping at different time slot without a synchronization mechanism. So there exists time skew not only between the CH sequences of the two radios of the same node, denoted as δi, but also between the CH sequences of the radios of two different nodes, denoted as δij.Similar with the single-radio scenario, here we still assume thatalways starts hopping earlier than(because of＞) for node i if δi＞ 0, and node i always starts earlier than node j if δij＞0, so δi∈[0,) and

Collision AvoidanceCompared with the single-radio scenario, the radio collision should be seriously considered in multi-radio scenario. The radio collision occurs when the two radios of the same node hop on the same channel at the same time slot. In the MRRCLR algorithm, when the two radios hops on the same channel at time slot t, the radiorandomly selects a channel from Cito attempt rendezvous with node j without changing its CH sequences. Radiodoes nothing to resolve the collision and just continue hopping on its original CH sequence. If theis replaced with the randomly selected channel, the rotation property of the whole CH sequence of each radio will be invalid, so collision is resolved temporally here.

Theorem 2For the multiple radio scenario, the rendezvous between the two nodes i and j is always guaranteed withintime slots.

Proof:It should be noted that it does not matter whether δij＞ 0 or not, which can be proved by cas2 2 of Theorem 1.

Case 1:, guaranteed withintime slots, which is proved by the Theorem 4 of [2].

C a s e 2:o r

, guaranteed withintime slots, and can be proved based on Lemma 2 of [4].

Case 3: δi＞ 0, guaranteed withintime slots, and can be proved by case 2 of Theorem 1 in this paper.

V. PERFORMANCE EVALUATION

In this section, we will verify the theoretical results in Theorem 1 by comparing with the simulation results. For comparison purpose,the HH algorithm is also simulated. The comparisons are conducted by the following three metrics: i) guarantee of the rendezvous; ii)average/expected time to rendezvous (ETTR);and iii) channel load.

5.1 Simulation setup

The simulations are implemented in MATLAB R2016a in asynchronous environments. The asynchronous environment is guaranteed by varying the time skew between CH sequences of nodes i and j in range [0,Ti) on all possible values. The simulations are conducted in 2-node scenario, and the available channels of the two nodes are randomly selected from[1,100]. The common channels between them are also randomly selected from their available channel set.

We run simulations by varying the number of available channels of the two nodes in the following four periods with the corresponding threshold for CLR: i) 10−20 period (C=20,Tc=23); ii) 20−30 period (C=30,Tc=31); iii) 30−40 period(C=40,Tc=41); and iv) 40−50 period(C=50,Tc=53). For each period, we randomly select three pairs of values as the number of available channels for nodes i and j, as shown in Figs. 2 and 3. For each situation,the time skew between nodes i and j is varied in range [0,Ti) and the number of common channels varied in [1,|Cj|], and each run is repeated for 100 times. So the results in the simulations are got by combing 100Ti* |Cj|runs. The overlapping ratio is defined as the fraction of common channels between nodes i and j to the total number of available channels of node j, assuming |Ci|＞| Cj|. During the simulation, we randomly generate a 8-bit binary ID for each node at each run.

5.2 Single radio scenario

1) Verifications on the Theoretical Results:In this part, we will verify the theoretical results concluded in Theorem 1 by comparing with the simulation results in two situations when Tiand Tjare coprime (Ti≠ Tj) or not(Ti= Tj). We study the MTTR under varying time skew and different pairs of number of available channels of nodes i and j. For any two situations where the cycle length pairs of nodes i and j are totally same, their theoretical MTTRs are also same (Theorem 1), and the small differences in simulated MTTRs are caused by different pair number of available channel between them, as shown in Figs. 2(b)and (c) and Figs. 3(b) and (c). In addition,Both Figs. 2 and 3 show that the simulation results are totally consistent with the theoretical results in Theorem 1: i) MTTR increase by cycle lengths of the two nodes. ii) The MTTR linearly increase by the time skew when Ti≠ Tj(Figure 2), while the MTTR is independent with the time skew when Ti= Tj(Figure 3). Also, the simulated MTTRs are always smaller than the theoretical MTTR.

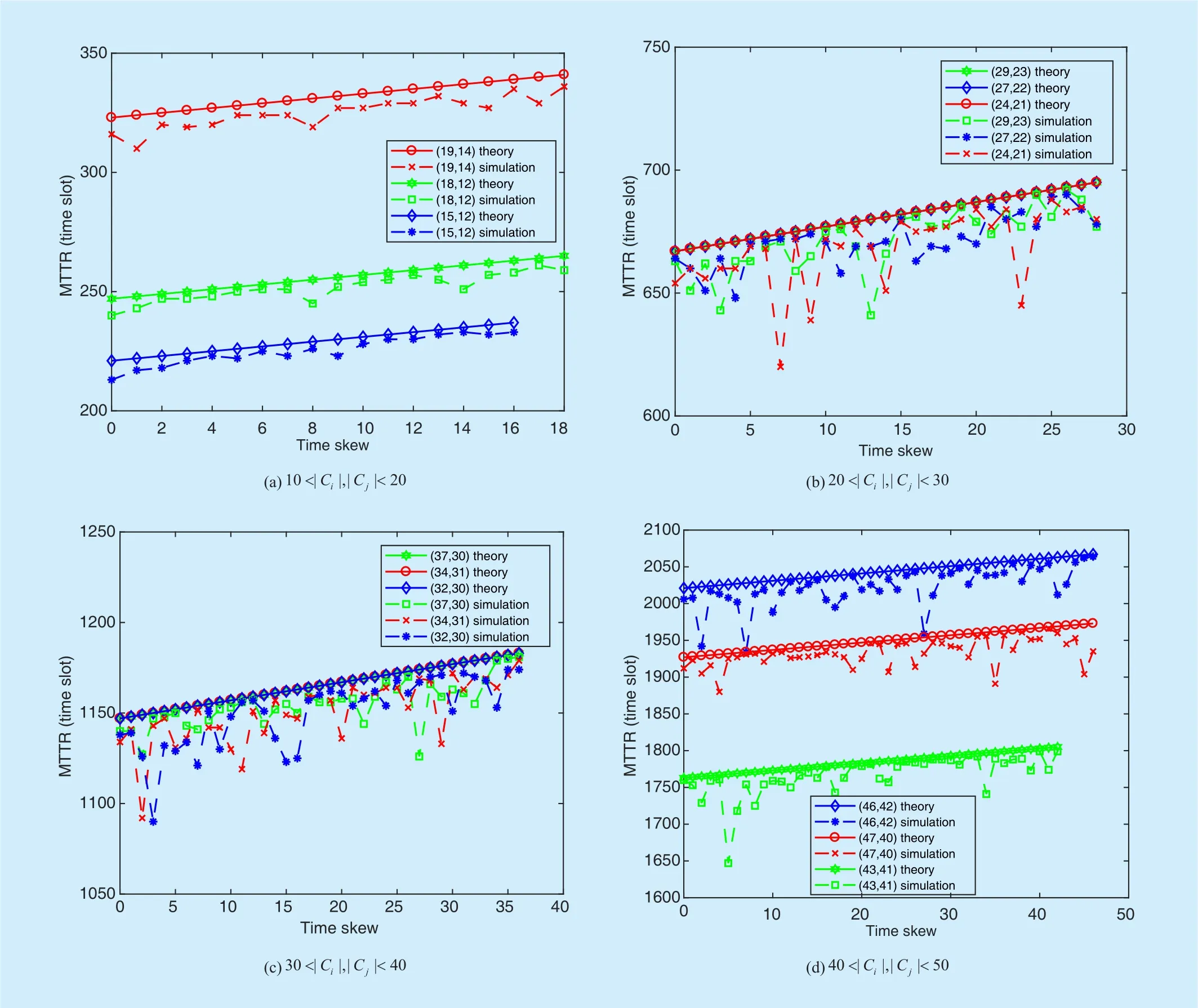
Fig. 2. Theoretical and simulated MTTR when Ti and Tj are coprime under varying time skew and different pair number of available channels of nodes i and j.

2) The Guarantee of Rendezvous: We study the guarantee of rendezvous under the varying overlapping ratio. By applying deadlock checking and the binary ID of each node, to independently change its cycle length bit by bit, the rendezvous of CLR algorithm is guaranteed in both the two situations, as shown in Figs. 4(a) and (b). While the rendezvous of HH algorithm is not guaranteed for both the two situations.

For HH, when the number of available channels of the two nodes are large, but the overlapping ratio is small, nodes i and j may rightly miss with each other on the common channels at some time skew due to its interspersed CH seuqences. Thus in Figure 4(a),the rendezvous of HH in 40−50 period is not guaranteed when the overlapping ratio is less than 0.3. In addition, due to the randomness in the channel IDs, theorem 7 of [2] is not valid, where the rendezvous can not be guaranteed. Thus at Figure 4(b), the rendezvous of HH is not guaranteed in 20−30, 30−40 and 40−50 periods as the overlapping ratio is less than 0.4,0.4,0.3, respectively. Especially for 10−20 period, the randomness in the channel IDs becomes more obvious when the number of available channels are small. Thus at Figure 4(b), the HH in 10−20 period is not guaranteed until the overlapping ratio is 1. As the number of available channels of the two nodes decrease, HH can not guarantee rendezvous with higher probability.

Fig. 3. Theoretical and simulated MTTR when Ti = Tj under varying time skew and different pair number of available channels of nodes i and j.

3)Expected Time to Rendezvous: We study the ETTR under the varying overlapping ratio. When Tiand Tjare coprime, the TTR between the two nodes is linear to the cycle length of their CH sequences. Since the cycle length of HH is three times of that of CLR,CLR always outperforms HH significantly under all of the four periods, as shown in Figure 5(a). When Ti= Tj, as the probability of failed rendezvous by HH is larger than 0.05(Figure 4b), the ETTR of HH is much higher than CLR in thousands, as shown in Figure 5b in 30−40 and 40−50 periods at the overlapping ratio of 0.1, and the 20−30 period at 0.1− 0.2. Especially for the 10−20 period, HH always has much higher ETTR than CLR till full overlapping ratio of 1. The use of threshold to guarantee rendezvous discounts the ETTR of CLR. Thus, when the overlap-ping ratio is larger than 0.2, the ETTR of CLR is higher than that of the HH. But CLR has a more stable performance that always guarantees rendezvous and has ETTR within 3000 time slots. So the trade off between the guaranteed rendezvous and the ETTR is important,and we can change the threshold to adjust the ETTR of CLR.

Fig. 4. Success rate under varying overlapping ratio.

Fig. 5. ETTR under varying overlapping ratio.

4)Channel Load: In CRNs, the channels available to each node are dynamically changed due to PUs’ activities. Therefore, the channel load is an important measure to evaluate rendezvous algorithms.is defined as set of probabilities, where lciis channel load of channel ci, the probability of rendezvous occurring on channel ciconsidering all the 300Ti· |Cj| runs on the algorithm for each period. The smoother the distributions of channel load, the better the algorithm is. So the channel load min-max degree d is defined as follows:

Fig. 6. Channel load distributions when Ti and Tj are coprime.

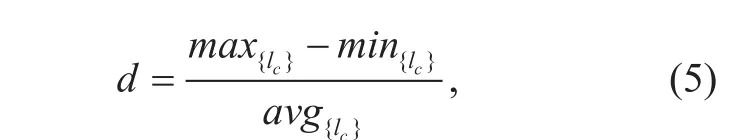
where max{lc}, min{lc}and avg{lc}represent the minimal, maximal and average of the channel load. The d quantifies the distance between the maximal and minimal channel load among all the channels. Thus the smaller d is,the better the algorithm is.

The channels are all randomly assigned with IDs from [1,100]. The CH sequence of CLR occupies each channel with almost the same probability without depending on the channel IDs, so the channel load is smoothly distributed on each channel for all situations,as shown in both Figs. 6 and 7. While the CH sequences of HH depends on channel IDs significantly by assigning the channel with smallest ID to the parity slots. So with HH,the channel with smaller IDs suffers from much higher channel load than other channels.Tables 2 and 3 demonstrate the channel load min-max degree for CLR and HH at all the four periods in the two situations respectively.Tables 2 and 3 also verify the results shown in Figs. 6 and 7, where the channel load min-max degrees of CLR are always much smaller than that of HH for all situations.

Fig. 7. Channel load distributions when Ti and Tj are not coprime.

5.3 Multiple Radio Scenario

In this part, we will evaluate the proposed MR-RCLR algorithm by comparing with the local sequence based rendezvous (LSR) algorithm proposed in [12].

For the simulation under the multi-radio scenario, we still divide the simulation into 4 cases including different range of the available channels of the two nodes. In each case, four pairs of available channels for the two nodes are simulated, in which both the coprime and not coprime situations are studied. As for the asynchronous setting, the radios of the samenode start hopping at the same time, while different nodes may start hopping at different time, with time skew

Table II. Min-max degree when Ti and Tj are coprime.

Table III. Min-max degree when Ti and Tj are not coprime.

Besides the ETTR, we introduce a new metric, radio diversity, to evaluate the rendezvous algorithm under multi-radio scenario. The radio diversity is defined as the percentage of rendezvous points where more than one pair of radios between the two nodes rendezvous with each other at the same time slot over different channels considering all theruns on the rendezvous algorithm. For example,the two pairs of radiosandcan rendezvous at the same time slot over two different channels, similar with the two pairsand

1) ETTR: The ETTR is studied over varying overlapping ratio between the two nodes.As shown in Figure 8, the ETTR of MRRCLR amd LSR over different periods of number of available channels are illustrated.It is clear that the ETTR given by MR-RCLR(solid lines) is always smaller than that given by LSR (dashed lines) over all the four periods. In LSR, two different cycle lengths are assigned to the two radios of each node, which causes higher ETTR because of the higher cycle length thanowned by one of the two radios.

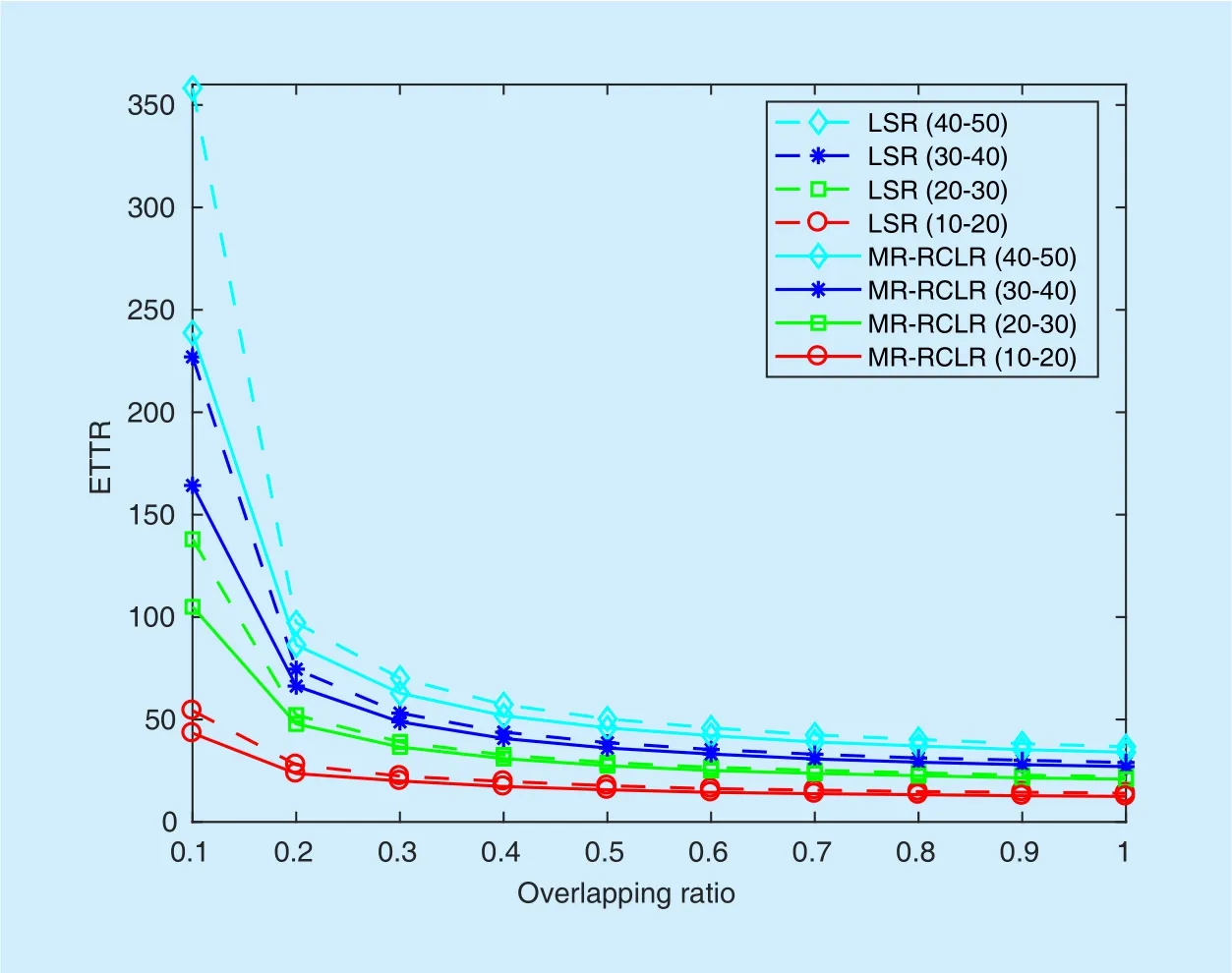
Fig. 8. ETTR over the four periods under varying overlapping ratios.

2) Radio Diversity: The radio diversity not only quantifies the radio efficiency but also the channel efficiency. In detail, a larger radio diversity given by a multi-radio rendezvous algorithm means that, there is a higher probability that both the two radios on both the two sides are fully utilized. In addition, higher radio diversity leads to higher possibility that more than one common channels can be found as the communication channels at the same time. The number of folds of diversity is defined as the possible number of pairs of radios that could be able rendezvous with each other at the same time slot. For example, in this paper, we consider two radios on each node, the maximal possible number of radio diversity folds is 2,and, andandare the two possible diversity situations. Figure 9 shows the comparisons on the radio diversity between the MR-RCLR and LSR algorithm. During all the three periods, 10−20, 30−40 and 40−50, the radio diversity of MR-RCLR is higher than that of LSR under both the two diversity situations(Figs. 9 (a), (c) and (d)).

VI. CONCLUSION

This paper firstly proposes a rendezvous algorithm named cycle length based rendezvous(CLR) algorithm for single-radio CRNs. The CLR guarantees rendezvous no matter Tiand Tjare coprime or not, where Tiand Tjare the cycle lengths of nodes i and j, respectively.To guarantee rendezvous when Tiand Tjare not coprime, we introduce a new strategy that combines the threshold based deadlock checking and the bit-by-bit cycle length changing scheme. The cycle length is oscillated betweenandbased on each bit of the node ID at each time point where the deadlock situation is detected. The rendezvous between the two nodes is reached as long as node IDs are different. We have conducted both theoretical and simulation studies to evaluate the performance of the CLR algorithm. Results demonstrate that the CLR algorithm outperforms the well-known heterogeneous hopping (HH)algorithms.

Fig. 9. Percentage of times where rendezvous occurs on both the two radio pairs over two different channels. and are twopossible folds of diversities when considering two radios on each node.

We then present a rotation and cycle length based rendezvous algorithm (MR-RCLR) for multi-radio CRNs. In MR-RCLR algorithm,rotations are applied to the initial CH sequence by each radio of each node, and the rendezvous between nodes i and j is always guaranteed no matter Tiand Tjare coprime or not.In detail, as long as any pair of radios of the two nodes choose different number of rotations when the cycle lengths of the two nodes are not coprime, the rendezvous between them can be reached.

ACKNOWLEDGMENT

The research was supported in part by NSF under the grant CNS-1526152.

[1] V. Brik, E. Rozner, S. Banerjee, and P. Bahl, “Dsap:a protocol for coordinated spectrum access,”in First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks,2005. DySPAN 2005., Nov. 2005, pp. 611–614.

[2] S. H. Wu, C. C. Wu, W. K. Hon, and K. G. Shin,“Rendezvous for heterogeneous spectrum-agile devices,” in IEEE INFOCOM 2014 - IEEE Conference on Computer Communications, April 2014,pp. 2247–2255.

[3] Y. Zhang, Q. Li, G. Yu, and B. Wang, “Etch: Effi-cient channel hopping for communication rendezvous in dynamic spectrum access networks,”in 2011 Proceedings IEEE INFOCOM, April 2011,pp. 2471–2479.

[4] H. Liu, Z. Lin, X. Chu, and Y. W. Leung, “Jumpstay rendezvous algorithm for cognitive radio networks,” IEEE Transactions on Parallel and Distributed Systems, vol. 23, no. 10, pp. 1867–1881,Oct. 2012.

[5] J. Li, H. Zhao, J. Wei, D. Ma, and L. Zhou, “Sender-jump receiver- wait: a simple blind rendezvous algorithm for distributed cognitive radio networks,” IEEE Transactions on Mobile Computing, vol. PP, no. 99, pp. 1–1, 2017.

[6] L. A. DaSilva and I. Guerreiro, “Sequence-based rendezvous for dy- namic spectrum access,” in 2008 3rd IEEE Symposium on New Frontiers in Dynamic Spectrum Access Networks, Oct 2008,pp. 1–7.

[7] C. Xin, M. Song, L. Ma, and C. C. Shen, “Rop:Near-optimal rendezvous for dynamic spectrum access networks,” IEEE Transactions on Vehicular Technology, vol. 62, no. 7, pp. 3383–3391, sept.2013.

[8] K. Bian, J. M. Park, and R. Chen, “Control channel establishment in cognitive radio networks using channel hopping,” IEEE Journal on Selected Areas in Communications, vol. 29, no.4, pp. 689–703, April 2011.

[9] B. Yang, M. Zheng, and W. Liang, “A time-effi-cient rendezvous al- gorithm with a full rendezvous degree for heterogeneous cognitive radio networks,” in IEEE INFOCOM 2016 - The 35th Annual IEEE International Conference on Computer Communications, April 2016, pp. 1–9.

[10] Z. Gu, H. Pu, Q. S. Hua, and F. C. M. Lau, “Improved rendezvous algorithms for heterogeneous cognitive radio networks,” in 2015 IEEE Conference on Computer Communications (INFOCOM), April 2015, pp. 154–162.

[11] Z. Gu, Y. Wang, Q.-S. Hua, and F. C. Lau, Rendezvous in Distributed Systems. Springer, 2017.

[12] G. Li, Z. Gu, X. Lin, H. Pu, and Q.-s. Hua, “Deterministic distributed rendezvous algorithms for multi-radio cognitive radio networks,” in Proceedings of the 17th ACM International Conference on Modeling, Analysis and Simulation of Wireless and Mobile Systems, ser. MSWiM ’14.ACM, 2014, pp. 313–320.

[13] R. Paul, Y. Z. Jembre, and Y. J. Choi, “Multi-interface rendezvous in self-organizing cognitive radio networks,” in 2014 IEEE International Symposium on Dynamic Spectrum Access Networks(DYSPAN), April 2014, pp. 531–540.

[14] L. Yu, H. Liu, Y.-W. Leung, X. Chu, and Z. Lin,“Multiple radios for fast rendezvous in cognitive radio networks,” IEEE Transactions on Mobile Computing, vol. 14, no. 9, pp. 1917–1931, 2015.

[15] ——, “Adjustable rendezvous in multi-radio cognitive radio networks,” in Global Communications Conference (GLOBECOM), 2015 IEEE.IEEE, 2015, pp. 1–7.

[16] A. Al-Mqdashi, A. Sali, N. Noordin, S. J. Hashim,R. Nordin, and M. J. Abdel-Rahman, “An efficient quorum-based rendezvous scheme for multi-radio cognitive radio networks,” in Telecommunication Tech- nologies (ISTT), 2016 IEEE 3rd International Symposium on. IEEE, 2016, pp.59–64.

[17] B. Yang, W. Liang, M. Zheng, and Y.-C. Liang,“Fully distributed channel-hopping algorithms for rendezvous setup in cognitive multiradio networks,” IEEE Transactions on Vehicular Technology, vol. 65, no. 10, pp. 8629–8643, 2016.

[18] T.-Y. Lin, K.-R. Wu, and G.-C. Yin, “Channel-hopping scheme and channel-diverse routing in static multi-radio multi-hop wireless networks,” IEEE Transactions on Computers, vol. 64,no. 1, pp. 71–86, 2015.

[19] K. Bian et al., “Maximizing rendezvous diversity in rendezvous proto- cols for decentralized cognitive radio networks,” IEEE Transactions on Mobile Computing, vol. 12, no. 7, pp. 1294–1307, 2013.

[20] I.-H. Chuang, H.-Y. Wu, and Y.-H. Kuo, “A fast blind rendezvous method by alternate hopand-wait channel hopping in cognitive radio networks,” IEEE Transactions on Mobile Computing, vol. 13, no. 10, pp. 2171–2184, 2014.