基于T-S模糊模型的高速动车组通信网络实时控制方法

张 彤

(大连交通大学 动车运用与维护工程学院,辽宁 大连 116028)

列车通信网络(Train Communication Net，TCN)是列车控制系统的重要组成部分，各种控制信号都通过其中的绞线式列车总线(Wire Train Bus，WTB)和多功能车辆总线(Multifunction Vehicle Bus，MVB)传送至对应的执行单元[1]。由于多种原因信息传输中会产生时延，如果时延过大将影响控制系统的稳定性[2]。

近几年，国内外已经开始关注列车通信网络控制技术中调度算法和控制方法的研究。如文献[3—4]针对现场总线(PROFINET)和MVB的调度算法进行了深入研究；文献[5—6]分析了由以太网—MVB和以太网—控制器局域网络(CAN)组成的列车通信网络控制方法时延问题。然而，作为另外主要列车通信网络的TCN，对其时延控制方法的研究却较少。

列车控制系统大多具有复杂的非线性特性，使其在建模、控制和诊断等方面的研究难度较大。由于T-S模糊模型可以任意精度逼近非线性模型，且其鲁棒性较强，受干扰和参数变化的影响较小，目前已被广泛应用于非线性网络控制系统的跟踪控制、稳定性等问题的相关研究中[7-10]。

本文在搭建多功能车辆总线的网络控制系统、采集时延数据的基础上，研究时延分布特性，利用自适应AR模型精确预测前向通道时延。采用T-S模糊模型对非线性系统进行建模，为各子线性系统设计广义预测控制器。最后，在TCN网络平台上对上述方法的有效性和正确性进行仿真和验证。

1 高速动车组网络控制系统

研究高速动车组通信网络控制系统时延问题的前提是，建立时延描述或预测模型、掌握时延传输特性。

典型的动车组通信网络控制系统由2个中央控制单元(Central Control Unit，CCU)和1个显示屏(Human Machine Interface，HMI)组成，它们都以过程数据在MVB上进行通信。CCU1作为控制器节点，实现对制动、牵引系统的控制，利用组态软件将控制算法植入CCU1中，根据传感器节点测得的最新数据计算控制量，再发送给执行器节点CCU2接收；CCU2作为执行器节点，模拟制动或牵引的执行过程，将执行结果发送给传感器节点；HMI作为传感器节点，实现系统输出信号的测量并发送给CCU1。因此，网络控制系统的传输时延包含2部分，即控制器节点与执行器节点之间的前向通道时延τca以及传感器节点与控制器节点之间的反馈通道时延τsc，则整个系统的网络时延为τ=τsc+τca。MVB一般网络控制系统结构如图1所示。

图1 MVB一般网络控制系统结构

在网络系统中，利用网络分析仪与软件相配合以获取大量前向和反馈通道时延数据。为更好地模拟高速动车组实际的运行组态，在CCU1中编写与实际应用一致的若干子任务、逻辑和大量端口。将各节点设置为与实际动车组运行相同的特征参数，包括任务类型和周期、节点类型和周期、特征周期、采样周期、优先级等。同一变量的发送模块特征周期与接收模块特征周期一致。

TCN中2个总线上的所有控制指令都是通过过程数据的源寻址广播方式进行传输[11-12]。WTB和国际铁路联盟(UIC)初运行完成后，各节点的时钟不一致，且由于过程数据更新较快，无法利用时间戳随时校正。需要在测量时延数据前，分析出各节点的时钟差，在各子设备软件中对控制输入和执行输入进行分别修正，使控制器提取最新的测量数据，得到准确的控制量输出预测值。

精确预测前向通道时延，才能合理调整控制量序列，抑制时延对网络控制性能的影响。通过分析大量过程数据中前向通道时延的数据样本，发现这些数据没有特定的概率分布特征，呈现出随机分布的特点，无法用线性模型进行有效描述，需要采用有效的方法实现随机时延的在线递推预测。

2 基于AR模型的LMS前向通道时延预测方法

最小均方算法(Least Mean Square，LMS)具有递推动态调整的特点，因此采用该方法可以根据实时时延数据自适应更新模型参数。高速动车组通信网络时延的自动回归(Auto Regressive，AR)预测模型为

(1)

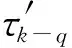
(2)

其中，

φk=(φ1kφ2k…φpk)T

Γk=(τk-1τk-2…τk-p)T

式中：Γk为k时刻以前的p个时延构成的矩阵。

式(2)中，p的选择与φk的计算精度有关，p越大得到的φk越精确，但是计算量也较大。需要根据所测时延数据反复调整p，达到计算精度和计算速度兼顾的目的。

为使残差平方的期望最小，利用最速梯度下降法求下一时刻加权系数向量φk+1，该向量等于现在时刻加权系数向量φk加上1个负均方误差梯度项-μ(k)，梯度项的大小由收敛因子μ决定，有

φk+1=φk-μ(k)

(3)

又由于

(4)

由式(3)和式(4)可得

φk+1=φk+2μεkΓkμ∈(0,λmax)

(5)

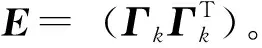
根据式(1)、式(2)和式(5)即可对网络时延模型的加权系数进行估计，并对未来时刻的时延进行估计。

3 基于T-S模糊模型的GPC时延控制方法

T-S模糊模型以模糊规则的形式充分利用系统局部信息和专家控制经验，可以任意精度逼近实际非线性不确定被控对象。考虑司机控制台对制动力和牵引力的控制是多级位、多区间的特点，可以利用T-S模糊模型光滑的描述1个高速列车非线性动力学过程。

3.1 非线性网络控制系统的T-S模糊建模

yi(k)=a0i+a1ix1(k-τk)+a2ix2×

(k-τk)+…+amixm(k-τk)

(6)

式(6)包含多个模糊规则，每一条模糊规则的后件参数均不相同，代表不同工况下的输入/输出关系后件具有线性时变特性，可以采用合适的线性方法对其进行控制，得到系统的输出为

(7)

通过模糊C-均值聚类(Fuzzy C-Means，FCM)算法获得模糊模型前件，规则后件通过制动或牵引系统的输入输出数据辨识得到。

FCM算方法是用隶属度确定每个数据点属于某个聚类中心程度的一种算法[13]，通过最小化聚类训练目标函数来实现，为

(8)

其中，

di(k)=‖x(k)-vi‖2

∑μi(k)=1

式中：Im为聚类训练的目标函数；di(k)为第i个聚类中心vi与第i个数据点x(k)间的欧几里德距离；μi(k)为每个聚类中心的隶属度；m为加权指数，通常取2。

3.2 基于状态空间的子模型GPC控制

(9)

其中，

A(z-1)=1+a1z-1+a2z-2+…+anz-n

B(z-1)=1+b1z-1+b2z-2+…+bnz-n

Δ=1-z-1

式中：A(z-1)和B(z-1)为后移算子z-1的多项式， 它们的最大阶数为n；u(k-τk-1)和ζ(k)分别为系统的输入和均值为0的白噪声序列。

将式(9)转换为预测时延的状态空间观测器模型[15]，为

(10)

其中，

B=(b1b2…bn-1)T

C=(1 0 … 0)T

东半壁店小流域总面积11.42km2，土地利用以耕地为主，耕地面积671.02 hm2，占小流域总面积的59%；其次为工业用地，面积为205.80 hm2，约占小流域总面积的18%；公路用地、沟渠、水面、农村道路、设施农用地、住宅用地分别占小流域总面 积 的 3%、1%、2%、0.4%、10%、8%。东半壁店小流域包括东半壁店、张各庄、倪家村、辛庄营4个村，总人口3 410人。土壤以黏底轻壤质潮土、夹黏轻壤质潮土为主。东半壁店小流域内植被属典型的针阔混交林类型，主要分布有乔木类、灌木类、草类植物。根据水利普查成果，小流域侵蚀面积为2.14km2，全部为轻度侵蚀，占总面积的比例为18.77%。

g=(-a1-a2… -an-1)T

式中：X(k)为n维状态预测向量。

定义性能指标J为

(11)

式中：Δu(k+j-τk-1)为控制增量；yr(k+j)为输入参考信号；E为数学期望；P和M为预测步长和控制步长；λ为控制加权系数。

Δu(k)=K1[Yr-f(FkY1+HkU1)]

(12)

其中，

Yr=(yr(k+τk)yr(k+τk+1) …

yr(k+p))T

f=(CCA…CAN-1)T

K1=(GkT+λI)-1GkT

式中：Y1为y(t)和y(t)之前的输出构成的矩阵；U1为Δu(k-τk)以前的输入构成的矩阵。

由式(12)可以得到下一时刻的最优控制率为

u(k-τk)=u(k-τk-1)+Δu(k)

(13)

预测控制过程基于实际过程获得的最新输入、输出和时延信息，同时实现每个子线性模型的滚动优化。

4 仿真分析

以文献[16]中的制动非线性系统模型作为被控对象，模型输入为制动力，输出为列车速度，分别采用考虑时延的基于T-S模糊模型GPC时延控制方法、不考虑时延的基于T-S模糊模型GPC控制方法和模糊自适应PID时延控制方法进行仿真，对比3种情况下的速度跟踪曲线，验证本文方法的有效性。进一步的，为深入剖析不同因素对时延和控制性能的影响，针对不同采样周期的跟踪特性和不同负载率下时延预测效果进行了仿真对比。

利用Unicap软件将模型建立于模拟制动系统的CCU2中，并在CCU2执行器中储存最新控制量信息。在控制器CCU1中辨别最新测量的速度数据，将时延预测算法、T-S模糊建模和GPC控制方法植入其中，协同计算出最新制动力预测值，并赋给制动系统模拟单元执行相应动作。在制动系统模拟单元中获取速度变量数据包作为系统实际运行数据。配置制动模拟设备任务执行周期50 ms。时延变化特性受众多因素影响，端口特征周期越快，端口数目越多，任务个数越多，时延变化越剧烈。将所测时延数据与其他变量放在同一任务中执行，以实现同步计算。建立有5条模糊规则的T-S模糊模型，设计5个广义预测控制器。预测步长P=20，控制步长M=3，控制加权系数λ=0.1，收敛因子μ=0.1，模糊隶属度函数选择Z函数。

4.1 采用不同控制方法时的控制效果

实际应用中，发送和接收端口的特征周期通常取64 ms的整数倍。当特征周期是64 ms时，前向通道时延和反馈通道时延值介于228和0 ms之间(因子设备时钟不一致)。将采用基于T-S模糊模型的GPC时延控制方法与不考虑时延的控制方法的输出效果作比较。当参考速度信号变化相对较慢时，跟踪方波输出响应曲线如图2所示。从图2可以看出：采用基于T-S模糊模型的GPC时延控制方法时，制动开始时速度输出有些滞后，随着时间增加，能很快精确跟踪方波，没有超调；而采用不考虑时延的控制方法时，则每次跳变瞬间输出剧烈震荡，2 s后才能达到稳定。

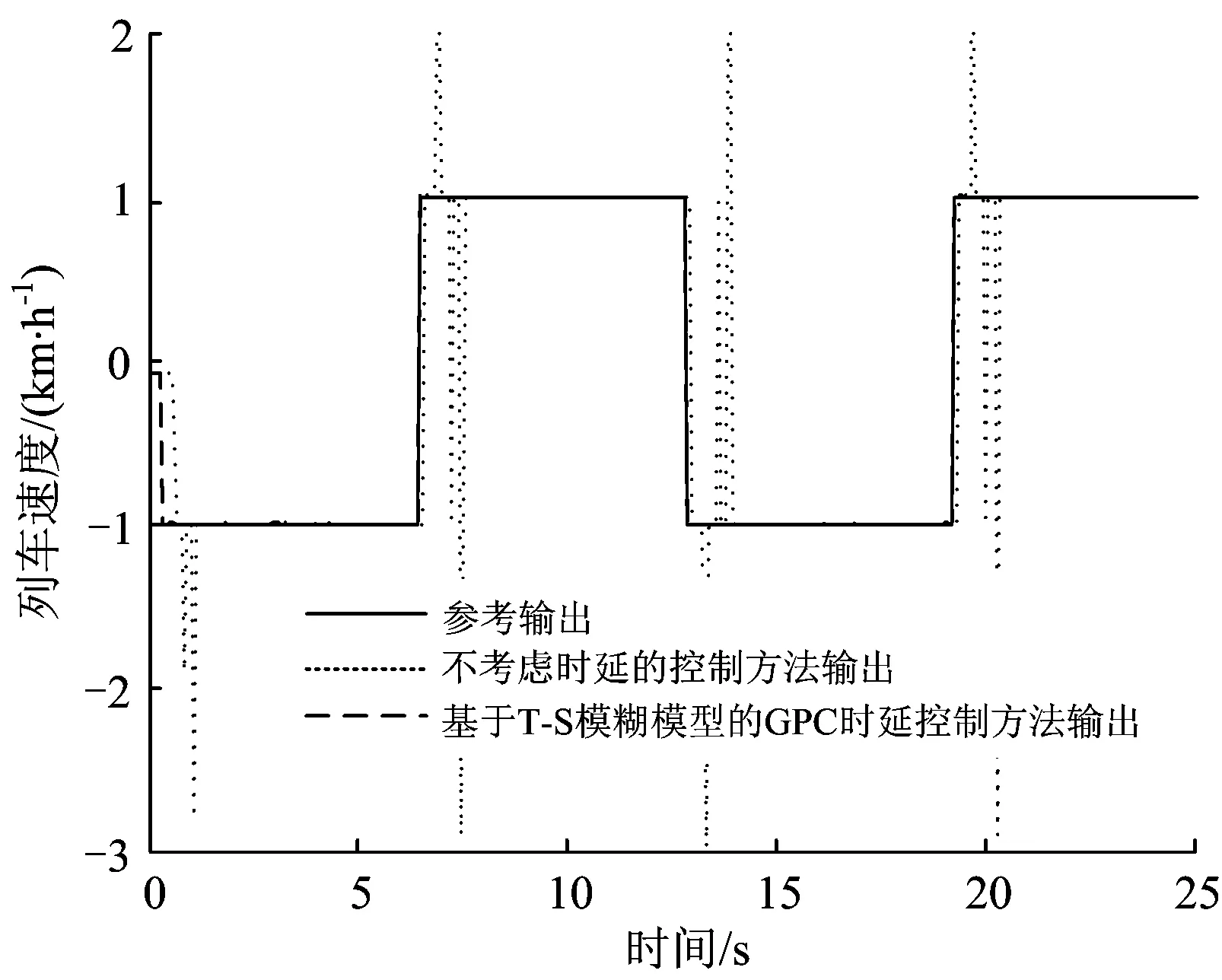
图2 参考速度信号变化较慢情况下的控制效果比较

考虑到未来更快速制动的需求，以参考速度信号变化频率快于前例10倍为例进行仿真，得到跟踪方波输出响应曲线如图3所示。从图3可以看出：采用基于T-S模糊模型的GPC时延控制方法时依然可以较好地跟踪方波变化，没有超调；而采用不考虑时延的控制方法时输出在非零区间反复震荡，无法满足跟踪方波的要求。

图3 参考速度信号变化较快情况下的控制效果比较

当设置制动力和速度的特征周期为128 ms时，前向和反馈通道时延加和的平均值增加至300 ms以上，如果不采用时延控制策略，则系统输出根本无法跟踪参考速度信号。采样周期为64 ms时基于T-S模糊模型的GPC时延控制方法与模糊自适应PID时延控制方法的控制效果对比结果如图4所示。从图4可以看出：进行方波跟踪时，尽管模糊自适应PID时延控制方法具有一定的跟踪控制效果，但是基于T-S模糊模型的GPC时延控制方法的优势更突出，该方法跟踪精确，可以实现多个稳态工作点下各线性子模型的平滑切换；同时，进行速度跟踪时，基于T-S模糊模型的GPC时延控制方法在整个提速和制动阶段的控制性能均良好，满足高速列车对给定速度的高精度跟踪要求。可见，基于T-S模糊模型的GPC时延控制方法可以在合理采样周期下精确跟踪不同变化频率的参考信号，同时能较好地抑制时延对控制性能的影响，具有理想的鲁棒性能和稳定性能。

4.2 采用不同采样周期和负载率时的控制效果

特征周期会影响时延的控制效果。同样，采样周期的合理选择对于理想控制效果的获得也是至关重要的。特征周期为128 ms时，不同采样周期下采用基于T-S模糊模型的GPC时延控制方法时的控制效果图5所示。从图5可以看出：采样周期大时超调量较大，稳态响应时间更长。可见，TCN网络控制性能随采样周期的减少而提高。但是，采样周期过快会增加网络负载率，进一步增加时延。

图4 T-S模糊GPC与模糊自适应PID控制效果比较

图5 特征周期128 ms时不同采样周期的控制效果比较

标准规定，MVB总线的数据传输速率为1.5 Mb·s-1，当有大量旅客列车服务信息或其他功能要求较复杂时，软件应用会增加过程数据端口数量和信息传输量，这会加重网络负荷，增强时延时变特性。标准中也规定了MVB总线过程数据在整个基本周期的占时比不能超过60%，实际应用中也规定了MVB总线的通信负载率不能高于60%。负载率与端口数目、端口特征周期和数据打包时间有关，因此设置相关参数使网络负载率由10%变化至50%，测试多组时延数据，发现不同负载率下的时延平均值几乎相同，丢包极少，吞吐能力强。负载率分别为10%和45%时，采用基于AR模型的LMS预测方法对某端口数据包进行前向通道时延预测的结果如图6所示。从图6可以看出：负载率较高时，时延抖动较为剧烈；在时延跳变瞬间，预测结果由于其在线递推特性而稍差，考虑到预测误差一般都小于采样周期，因此对下一步时延补偿效果影响不大。

5 结 语

本文针对列车制动、牵引关键网络控制系统提出一种基于T-S模糊模型的控制策略。搭建网络平台测量时延并揭示时延的变化特性，根据时延随机变化的特点设计了自适应AR模型的LMS在线前向通道时延预测方法。利用T-S模糊模型对列车非线性网络控制系统进行建模，并对各线性子模型设计了广义预测控制器进行模糊加权控制。仿真结果表明，基于T-S模糊模型的GPC方法能够实现不同稳态工作点线性子模型的平滑切换，可以有效控制时延，快速、精确跟踪参考信号变化，具有理想的实时性能、鲁棒性能和稳定性能。本文的研究为列车通信网络的控制和软件设计提供思路，可以进一步增强高速动车组自动化与信息化程度，提高列车运行的经济性、安全性和可靠性。

图6 不同负载率时基于AR模型的LMS时延预测

[1] 刘建伟，王蕾，谭南林，等. 轨道车辆MVB 通信网络的实时特性[J].中国铁道科学，2006，27(6) ：79-83.

(LIU Jianwei，WANG Lei，TAN Nanlin，et al. Real-Time Performance of MVB Communication Network in Rail Vehicles[J].China Railway Science，2006，27(6)：79-83. in Chinese)

[2] 郭超勇. 高速动车组列车网络控制若干问题研究[D]. 北京：北京交通大学,2012.

(GUO Chaoyong. Research on Several Issues of High-Speed Electric Multiple Units Train Network Control[D]. Beijing：Beijing Jiaotong University,2012. in Chinese)

[3] 周洁琼，王立德. 基于PROFINET IRT的列车通信网络调度算法[J].北京交通大学学报,2016,40(3):7-13.

(ZHOU Jieqiong，WANG Lide. Scheduling Algorithm of PROFINET IRT Based on Train Communication Network[J].Journal of Beijing Jiaotong University，2016，40(3)：7-13. in Chinese)

[4] 王保华，严翔， 王立德，等. 基于负载均衡的MVB周期数据调度优化[J].中国铁道科学，2017，38(5)：114-120.

(WANG Baohua，YAN Xiang，WANG Lide，et al. Optimization of MVB Periodic Data Scheduling Based on Load Balancing[J].China Railway Science，2017，38(5)：114-120. in Chinese)

[5] 李辉，张和生，潘成，等. 动车组列车安全状态检测网络时延建模[J].机车电传动，2013(6)：75-81.

(LI Hui，ZHANG Hesheng，PAN Cheng，et al. Delay Modeling of Safety State Detection Network for EMUs[J]. Electric Drive for Locomotives，2013(6)：75-81. in Chinese)

[6] 严翔，王立德，杨宁，等. MVB-Ethernet网关设计与时延分析[J].北京交通大学学报，2014，38(2)：106-111.

(YAN Xiang，WANG Lide，YANG Ning，et al. Design and Analysis of MVB-Ethernet Gateway[J].Journal of Beijing Jiaotong University，2014，38(2)：106-111. in Chinese)

[7] 褚红燕，费树岷，岳东. 基于T-S模型的非线性网络控制系统的量化保成本控制[J].控制与决策,2010,25(1)： 31-36.

(CHU Hongyan，FEI Shumin，YUE Dong. Quantized Guaranteed Cost Control for T-S Fuzzy Nonlinear Networked Control Systems[J].Control and Decision，2010,25(1)：31-36. in Chinese)

[8] 肖会芹，何勇，吴敏，等. 基于T-S模糊模型非线性网络控制系统改进H∞跟踪控制[J].控制理论与应用，2012， 29(1)：71-78.

(XIAO Huiqin，HE Yong，WU Min，et al. Improved H-Infinity Tracking Control for Nonlinear Networked Control Systems Based on T-S Fuzzy Model[J].Control Theory & Applications，2012,29(1)：71-78. in Chinese)

[9] FRIDMAN Emilia. A Refined Input Delay Approach to Sampled-Data Control [J]. Automatics，2010，46(2)：421-427.

[10] MAROUF Sepideh, MAHBOOBI Esfanjani Reza, AKBARI Ahmad, et al. T-S Fuzzy Controller Design for Stabilization of Nonlinear Networked Control Systems [J]. Engineering Applications of Artificial Intelligence，2016，50(C)：135-141.

[11] International Electro Technical Commission.IEC61375-1 Electric Railway Equipment-Train Bus—Part 1: Train Communication Network[S]. Geneva:International Electro Technical Commission, 1999.

[12] 李常贤，刘洋，张彤，等.用于动车组间互联、互通和互操作的UIC网关研究[J].中国铁道科学，2013，34(6)：110-116.

(LI Changxian，LIU Yang，ZHANG Tong，et al. Research on UIC Gateway for Interconnection, Intercommunication and Interoperability between EMUs[J]. China Railway Science，2013，34(6)：110-116. in Chinese)

[13] 雷世昌. T-S模型的窑炉压力无超调快速广义预测控制设计[J].计算机与应用化学，2014，31(8)：977-981.

(LEI Shichang. None-Overshoot Fast Generalized Predictive Control Design for Furnace Pressure Based on T-S Model[J]. Computer and Applied Chemistry，2014，31(8)：977-981. in Chinese)

[14] 张日东，王树清，李平. 基于支持向量机的非线性系统预测控制[J].自动化学报，2007，33(10):1066-1073.

(ZHANG Ridong，WANG Shuqing，LI Ping. Support Vector Machine Based Predictive Control for Nonlinear Systems[J]. ACTA Automatica Sinica，2007，33(10)：1066-1073. in Chinese)

[15] 时维国，邵诚，孙正阳. 基于AR模型时延预测的改进GPC网络控制算法[J].控制与决策，2012，27(3)：477-480.

(SHI Weiguo，SHAO Cheng，SUN Zhengyang. Improved GPC Network-Control Algorithm Based on AR Model Time-Delay Prediction[J]. Control and Decision，2012，27(3)：477-480. in Chinese)

[16] 杨辉, 严瑾, 张坤鹏. 动车组制动过程多模型自适应PID控制[J]. 铁道学报, 2014, 36(3):42-48.

(YANG Hui，YAN Jin，ZHANG Kunpeng. Multiple-Model Self-Tuning Fuzzy PID Control of Braking Process of Electric Multiple Unit[J]. Journal of the China Railway Society，2014，36(3)：42-48. in Chinese)

[17] 李中奇，杨振村，杨辉，等. 高速列车双自适应广义预测控制方法[J].中国铁道科学，2015，36(6) ：120-127.

(LI Zhongqi，YANG Zhencun，YANG Hui，et al. Generalized Predictive Control with Dual Adaptation Method of High Speed Train[J].China Railway Science，2015，36(6)：120-127. in Chinese)

[18] BARRIOS Jos Angel，VILLANUEVA Cesar，CAVAZOS Alberto，et al. Fuzzy C-Means Rule Generation for Fuzzy Entry Temperature Prediction in a Hot Strip Mill[J]. Journal of Iron and Steel Research International,2016,23(2):116-123.

[19] LI Shujiang,WU Ying,WANG Xiangdong，et al.VAV Terminal Unit Control Based on T-S Model with the Generalized Predictive Control[J].Applied Mechanics and Materials,2013,303/304/305/306:1234-1237.

[20] WANG Baohua,WANG Lide,NIE Xiaobo，et al.Research and Design of MVB Bus Administrator Based on SOPC Technology[C]//IEEE International Conference on Industrial Technology.Toronto:IEEE,2017:1195-1198.