大规模风电并网对系统频率的影响分析

任振宇1，张师，周立新

(1.内蒙古电力集团有限责任公司，内蒙古 呼和浩特 010000 ；2.东北电力大学电气工程学院，吉林 吉林 132012)

1 引言

近年来，中国的严重雾霾所导致的环境污染引发了社会的普遍高度重视[1]。高效利用可再生能源发电，减少煤炭能源发电，是缓解环境问题的有效措施。预计在2030年我国可再生能源的用电率达到30%以上[2]。目前，风力发电作为技术最成熟的可再生能源发电形式，每年的新增装机容量正在迅猛增长。

随着风电并网容量的增加，风电功率的波动给电力系统频率稳定控制也带来了更多的挑战，因此，大规模风电并网对系统的频率影响是一项值得深入研究的课题[3-5]。

目前，风电并网对系统频率的影响研究已经取得一些成果，文献[6]基于实测数据研究了风电功率波动规律与风电功率波动对电网频率的影响；文献[7]研究了风电功率波动对电网频率动态过程的影响及风电机组参与调频的可行性；文献[8]基于功率滤波算法研究了风电功率波动对系统频率动态特性的影响。

基于以上研究，本文首先对风电机组建模，再分析风电功率波动对电力系统各台同步发电机频率动态行为的影响，最后，采用Matlab工具箱PSAT仿真验证本文结论有效性。

2 风电机组模型

本文将采用PSAT仿真分析，因此在风电机组建模部分采用PSAT中的双馈风力发电机(Double Fed Induction Generator，DFIG)的模型。DFIG的原动机模型如下：

(1)

式中：θp是桨距角，DFIG的原动机桨距角是可调的，通过调节桨距角可以实现转子转速调节和最有风功率捕获。

DFIG的发电机为绕线式异步电机，因此适合采用5阶模型分析，可以表示如下：

uds=-rSids+((xS+xm)iqs+xmiqr)

(2)

uqs=-rSiqs-((xS+xm)ids+xmidr)

(3)

udr=-rRidr+(1-ωm)((xR+xm)iqr+xmiqs)

(4)

uqr=-rRiqr-(1-ωm)((xR+xm)idr+xmids)

(5)

P=udsids+uqsiqs+udcidc+uqciqc

(6)

Q=uqsids-udsiqs+uqcidc-udciqc

(7)

(8)

(9)

式中：xS为定子电抗；xR是转子电抗；

xm是激磁电抗；ωS是定子侧频率；ωr是转子侧频率；ωc是电网频率。

DFIG输出的功率为要考虑定子侧功率和转子侧的功率。

DFIG的控制模型主要包括转子控制、电压控制、桨距角控制三个部分。

3 风电功率波动对系统频率的影响

系统中各台同步发电机的转子运动方程可以表示为：

(10)

式中：ωi为第i台同步发电机的转速；Tji为第i台同步发电机的惯性时间常数；PMi为第i台同步发电机的机械功率；PEi为第i台同步发电机的电磁功率。

当风电功率波动时，会影响各台同步发电机的电磁功率，从而造成各台发电机的转速发生变化，从而影响各台发电机的机端的频率。

设风电机组机端电压为Uwind，传统同步发电机的机端电压Usyn，风电机组和同步发电机间的等值电抗为Xwind-syn，电压相角差为δwind-syn；同步发电机与风电机组之间的传输功率可以表示为：

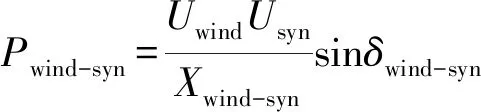
(11)

当风电功率发生波动时，会使风电机组的机端电压相角δwind发生波动，从而改变δwind-syn，根据公式(11)，会改变风电机组与同步发电机间的传输功率，从而改变同步发电机的电磁功率PEi。传输功率的波动大小与Xwind-syn成反比，当风电机组和同步发电机的机端电压一定时，Xwind-syn越大，同步发电机的电磁功率波动越小，转速变化越小，从而频率波动越小。

从以上分析可以看出，当风电功率发生波动，会使同步发电机的电磁功率也随之发生波动，当同步发电机距离风电机组越远，所受影响越小。此外，当同步发电机惯性较小时，频率也会受到较大影响。

4 算例分析

采用WSCC3机9节点系统算例，分析风电并网对系统频率的影响，PSAT的仿真算例如图1所示，网络额定电压230kV，额定频率60Hz，各台同步发电机采用经典二阶模型。

图1 DFIG接入WSCC3机9节点系统

图1中DFIG接入位置为bus9，在bus1、bus2、bus3分别接入了频率监测模块，设置DFIG为100台1MW的机组通过35kV箱变接入升压变压器，升至230kV电压等级接入电网。

风速模型采用合成风力模型，本文只采用其中的初始风速和随机风速两部分，风速设置如图2所示。

设置仿真时间20s，采用变步长积分，风速如图3所示，图4为bus1、bus2、bus3母线频率。

从图4可以看出，bus3的频率波动较大，这是由于bus9距离bus3最近，因此bus3的频率受扰较严重。此外，bus3所连的同步发电机惯性时间常数最低。为验证各台发电机惯性对频率波动的影响，将DFIG接入bus4，风速模型仍然采用合成风力模型，随机风速如图5所示。

图2 PSAT中的风速模块

图3 风速波动

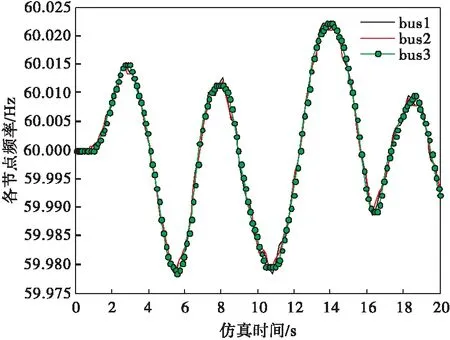
图4 bus1、bus2和bus3母线频率

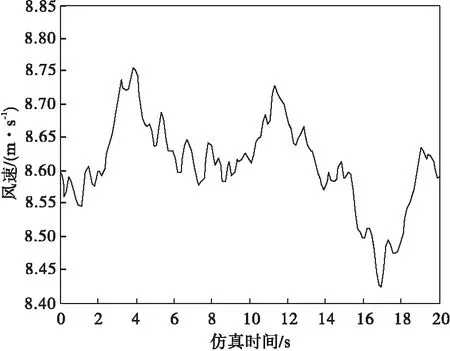
图5 风速波动

该风速扰动下，各母线的频率波动如图6所示。

图6 bus1、bus2和bus3母线频率

从图6可以看出，bus1、bus2和bus3母线的频率波动情况相差不多，尽管风电接入的位置距离bus1较近，但由于bus1所接的同步的发电机的惯性较大，因此bus1频率波动与其他节点频率波动情况相差不多。

5 结论

本文分析了大规模风电并网对系统频率的影响，通过分析可以得出以下结论：

由于系统各位置的发电机惯性不同，功率波动也不同，因此使得电力系统的频率也不同。

风电接入位置对系统频率动态过程有较大影响，在风速波动时，距离风电越近的节点，频率受扰越严重。

发电机惯性对频率也有较大影响，惯性越大，对风功率波动的抗扰能力越强，频率波动越小。