微电网混合储能系统控制策略研究及其应用
(1.东北电力大学电气工程学院, 吉林 吉林 132012;2.国网吉林省电力有限公司电力科学研究院, 吉林 长春 130000;3.国网吉林省电力有限公司,吉林 长春 130000;4.长春供电公司,吉林 长春 130000)
1 引言
随着雾霾、大气温度上升及化石资源短缺等环境问题进一步恶化,大力发展新型的清洁可再生能源已不可避免[1]。但是风速、光照等自然资源具有强间歇性,从而导致相关机组发电的功率出力具有明显的不确定性,在接入电网的同时不可避免的对电网整体的优化、运行及调度等工作带来一定的挑战,限制了其大规模的发展[2-3]。微电网(Micro-grid,MG)作为一种新型的发电模式,其因为含有充裕的储能系统容量配置,能在一定程度上缓解风、光发电的波动幅度,为其接入电网提供相关便利。
储能技术因为其拥有一定功率平滑性能,最近几年得到了大量学者们的关注,由于它可以对间歇性出力资源的输出功率进行一定程度平滑,因此其在间歇性能源发电系统等领域取得了巨大的成功和应用[4]。但是单一类型的储能技术因为其运行成本高、使用场合要求高和平滑效果差等因数的影响,具有一定的局限性,从根本上限制了其大规模发展[5]。相比于单一储能方式来说,混合储能系统(Hybrid Energy Storage System,HESS)具有无法比拟的优势,能更好、更快速的对外部功率特性曲线进行动态平滑,是现有微电网储能方式发展的一种新型有效手段[6-7]。文献[8]建立了混合储能的数学模型,提出一种MG中混合储能的优化配置数学模型,利用粒子群算法进行模型求解,有效改善了MG中的各项运行指标。文献[9]搭建了蓄电池-超级电容器混合储能模型,并提出了一种基于二阶低通滤波法的混合储能控制策略,该策略能够对光伏电站出力实现有效平滑。文献[10]在搭建蓄电池-超级电容器混合储能模块的基础上,对电池内部的充放电深度进行合理估算,同时建立混合储能系统综合成本最小的微电网优化配置模型,利用粒子群算法进行问题求解,具有很好的经济性能。以上文献深度分析混合储能在平滑微电网间歇性资源出力问题,具有很好的工程实用价值。
本文结合现有研究基础上搭建磷酸铁锂电池和超级电容器的混合储能模型;设计一种基于二阶低通滤波器原理的功率分配策略,合理分配储能系统的配置功率及容量;建立考虑微电网源荷侧不确定性出力的风力、光伏和负荷模型,分析搭建的混合储能系统在平滑微电网不确定出力上的高效性。
2 微电网储能系统工作特性分析
2.1 锂电池工作特性分析
常用的评价锂电池工作的性能参数主要有电池容量、荷电状态、放电深度,其对应的基本概念如下:
(1)电池容量
锂电池的电池容量就是在恒定的放电状态下,当其对应的端电压下降到临界电压的时刻,所释放出来的总电量,其对应的计算公式为:
Cdis=Idistdis
(1)
式中:Idis为放电电流(A);tdis为放电时间;Cdis为锂电池的放电容量(Ah)。
若放电过程中的放电电流非恒定,则需要采用积分的处理手段来计算其电池容量:

(2)
(2)荷电状态
锂电池的SOC指标常用于评估其在充放电状态下的实时剩余电量,其对应的计算公式如下:
(3)
式中:QR为评估时刻下锂电池剩余电量;Qsum为评估时刻下锂电池的最大释放容量。
如果将电池充满电状态定义为SOC=1,那么:
Qsum=QR+Q
(4)
结合公式(4),荷电状态的另外一种表达形式为:
(5)
式中:Q评估时刻下已释放电量。
(3)放电深度
锂电池的放电深度(depth of discharge,DOD)是指当前时刻下所释放出来的电量和能全部释放总电量的比值,其对应的计算公式如下:
(6)
DOD=1-SOC
(7)
2.2 超级电容器工作特性分析
超级电容器的电容大小与自身能存电量多少密切相关,本文将超级电容等效成一个理想电容和一个电阻并联,再与一个小电阻串联的形式,其对应的本征容量C定义为:
(8)
对应的数学模型如下:
通过实验来确定C=C(T(t),I(t))和R=R(T(t),I(t)),然后定义下式:

(9)
那么超级电容的端电压U和其开路电压Uc可得:
(10)
式中:U0为超级电容初始电压;Ileak为漏电流;R为等效内阻;C为本征容量;t为充放电时间。
参照荷电状态的定义,超级电容器的SOC可以表示为:
(11)
式中:Qremain表示残余电量;Qtotal表示总电量。
3 混合储能模块搭建
本文搭建的混合储能模块中锂电池等效为一个理想电压源和一个其对应的电阻串联模块,与此同时,超级电容器等效为一个理想电容和一个小电阻串联模块,同时通过功率变化器将锂电池和超级电容器并联,构成本文的混合储能系统,其对应的系统网络结构如图1所示。
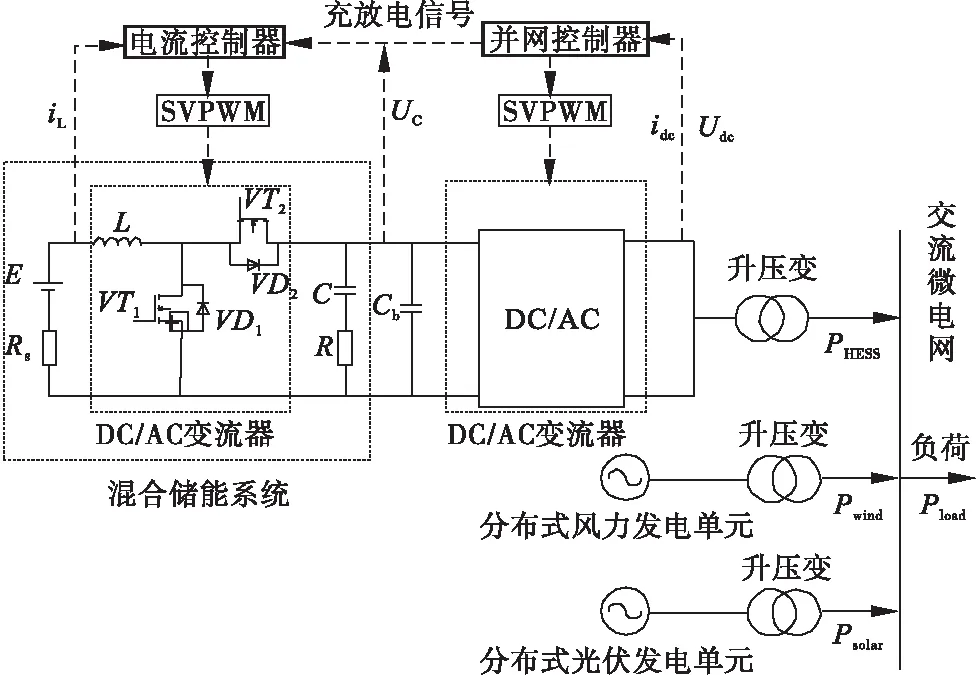
图1 微电网混合储能系统
图1中混合储能系统首先通过DC-AC变换器将直流源转化为交流源,再通过升压变压器单相接入电压等级为10kV的交流微电网中,其中锂电池模块与超级电容模块借助于DC-DC变流器并联接在一起,免去了锂电池两端电压和超级电容的电压要求必须一致的限制,该混合储能系统首先将超级电容器放置前段,与DC/AC变流器相连,充分发挥了功率密度大、相应时间短、可承受充放电次数多等优点,通过主动控制功率开关VT1、VT2来精确的控制锂电池的输出功率,优化其工作状态,从而避免过大功率、过于频繁的对锂电池进行充放电。图1中的并网控制器通过采集微电网侧的交流母线电压来生成储能系统输出电流的参考值,然后再同实际输出值相比较产生控制DC/AC变流器的SVPWM信号。而控制锂电池放电的DC/DC变流器中的SVPWM信号则是通过电流控制器采集的超级电容器端电压和并网控制器给出的充放电信号来生成输出电流参考值,同实际值进行比较而产生的。
4 混合储能系统功率分配策略
微电网中风、光互补系统能在一定程度上减少单一微电源的波动幅度,有效提高微网运行的可靠性,但是受外部环境因数的影响,其出力任然存在较强波动,对微网合理运行埋下潜在隐患。利用二阶低通滤波原理对混合储能功率进行分配,合理发挥各储能设备的优势。不考虑系统损耗因数的影响,微电网中风、光微电源的功率出力之和可以表述为:
PMC(t)=Pwind(t)+Psolar(t)=PHESS(t)+Pun(t)
(12)
式中:PMC(t)为t时刻微网实际输出的有功功率PHESS(t)为t时刻微网混合储能吞吐的有功功率;Pun(t)为t时刻微网总输出有功功率的一次目标值。
混合储能的吞吐功率值与微网实际有功功率输出值和接入电网的一次目标值密切相关,若PMC(t)小于Pun(t)时,混合储能应释放部分电量以补偿微网的有功功率;若PMC(t)大于Pun(t)时,混合储能应吸收部分电量以储存微网的有功功率。
在对两种储能装置进行功率分配研究之前,首先需要对原始输出功率进行频谱分析。利用傅里叶变换手段对原始输出的随机波动功率数值进行变换,得到其对应的功率波动频谱图如图2所示。

图2 傅里叶变换后的原始功率频谱
本文利用二阶低通滤波器原理对储能系统功率进行分配。由图3所示,Pun(t)为原始输出功率、PSC(t)为超级电容器运行功率、PBAT(t)为锂电池运行功率,经微电网储能系统平抑后的并网功率波动量大小由fBAT所决定,超级电容器与锂电池的功率波动平抑范围由超级电容器的低通滤波截止频率fSC决定。
根据确定的各自平抑范围选择与之对应低通滤波时间常数。二者的运行功率计算公式如下:

图3 二阶低通滤波器功率分配原理
(13)
(14)
5 微电网储能系统冲放电控制方法
对MG中HESS的每个储能单元的充放电状态进行监测能减少其发生过充或过放的现象,有效提高MG中HESS的工作效率并延长其使用寿命。本文考虑各储能单元的电量裕度,对混合储能单元中锂电池和超级电容器的实时SOC进行估计,合理的安排各储能装置所承担的充放电任务。
(1)当PHESS<0时
若混合储能模块中第i个电池的DOD值满足DODi≥DODmax,表示这个所对应的电池无法继续放电,则双向变流器上流动的功率为:
PHESS-i(t)=0
(15)
若混合储能模块第j个电池的DOD值满足DODj PHESS-j=-PHESS(t) (16) 式中:CHESS-j为第j个储能单元的基本容量;CHESS-j(DODmax-DODj)为第j个储能单元剩余容量。 (2)当PHESS>0时 若混合储能模块第i个电池的SOC值满足SOCi>SOCmax,表示这个所对应的电池无法继续充电,则双向变流器上流动的功率为: PHESS-i(t)=0 (17) 若混合储能模块第j个电池的SOC值满足SOCj PHESS-j=PHESS(t) (18) 式中:CHESS-j(SOCmax-SOCj)为第j个储能单元的可充电容量。 图4是在simulink中所搭建的单个混合储能系统仿真电路,其对应额定安装容量为500kW,其中单个超级电容器电芯型号为2.7V/200uf,单个锂电池型号为2.7V/20Ah,500kW混合储能系统中每一个电池模块由10个电芯串联,6个电芯并联组合,其对应的端电压为27V,端电流为120A,500kW混合储能系统中每一簇电池模块由26个电池模块组成,其对应的额定电压为702V,额定电流为760A,混合储能模块通过Boost电路级联在一起,并通过PCS控制电路接入电网。 图4 储能系统仿真模型 运行Matlab/Simulink中搭建的储能部分仿真电路。首先,对DC/DC电路输出电压进行分析,图5中给出了DC/DC电路仿真运行结果。 图5 DC/DC电路电压运行结果 可以看出,图5中直流电压经升压环节被调制为700V,调节过程迅速且无超调,表明DC/DC控制环节电压外环调节的有效性。 并网逆变器微电网混合储能与交流电网交互的桥梁,其运行性能直接决定了微电网混合储能系统对波动电网支撑的有效性。图6中给出了小功率支撑下并网逆变器稳态运行仿真结果。 图6 小功率支撑下并网逆变器稳态运行结果 可以看出,并网逆变器稳态电压、电流分布规律,其中图6(a)稳态线电压呈PWM波形特性,图6(b)稳态电流呈高正弦度特性,且总畸变率小于5%,满足并网电流运行要求。 为验证所采用的功率波动平抑策略及所设计的储能系统配置策略的合理性,给储能系统提供一个类似于微电网并网时刻的波动频率,时间常数设置为2400s,原始风力和光伏出力数据从matlab调用函数中直接导入至simulink数据组中,混合储能系统配置总容量不超过分布式资源的10%,取其值为7MW,考虑到单个混合储能模块的额定容量仅为500kW,因此需要并联10个混合储能单元才能满足实验要求。对一组随机生成的风、光不确定性功率出力进行平滑处理,原始风、光功率波形分布情况如图7所示。经过HESS平抑后的波形分布情况如图8所示。 由图8可知,在平滑原始功率波动性方面,采用HESS处理的效果比采用超级电容器的效果更佳,是因为MG中HESS的能量密度相对于单一储能方式来说有很大改善。最终输出的功率波形满足系统调度需求,证明了所搭建储能系统具有平抑功率波动的功能。 图7 原始并网功率分布情况 图8 经HESS平抑后并网功率分布情况 将超级电容和锂电池的充放电功率波形提取出来单独对比,两者的充放电曲线分布分别如图9、图10所示。 观察对比两组波形可以发现,图9中超级电容每个时间点的充放电量大且更加频繁;图10中锂电池各个时间点充放电电量较小且频率低。原因是因为本文的HESS采用二阶滤波原理,首先第一阶主要利用超级电容器平滑原始输出功率的高频波动分量及系统需要快速响应时锂电池的功率响应延迟量,然后再由第二阶的锂电池对其进行进一步的平滑。这样的设计可以高效的利用超级电容的特点,保证以锂电池在正常工作为前提,缓解其过多的充放电的压力,有效地增加了锂电池的效率运行时长。 图9 超级电容器充放电功率波形 图10 锂电池的充放电功率波形 本文基于二阶低通滤波法配置超级电容器与锂电池的功率及容量,在充分考虑储能系统的工作特性的前提下,同时考虑储能单元的放电深度以及荷电状态对系统充放电状态的影响,对锂电池和超级电容的平抑功率进行合理分配。仿真算例结果验证了该混合储能系统能够在有效平抑功率波动的前提下优势互补,超级电容高频率快速的充放功率,承担了更多高频波动平抑任务。此复合式储能组合有效降低了锂电池的充放电次数,在保证系统稳定的基础上,延长了锂电池运行时长。6 算例分析
6.1 混合储能模型分析
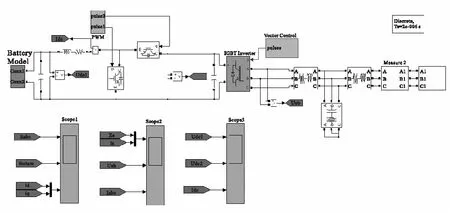

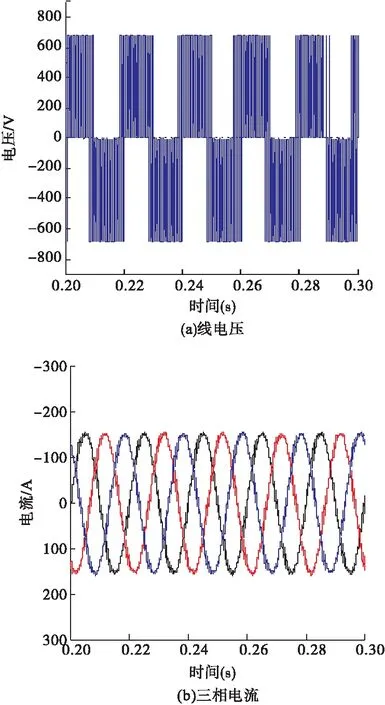
6.2 混合储能系统在微电网中的应用

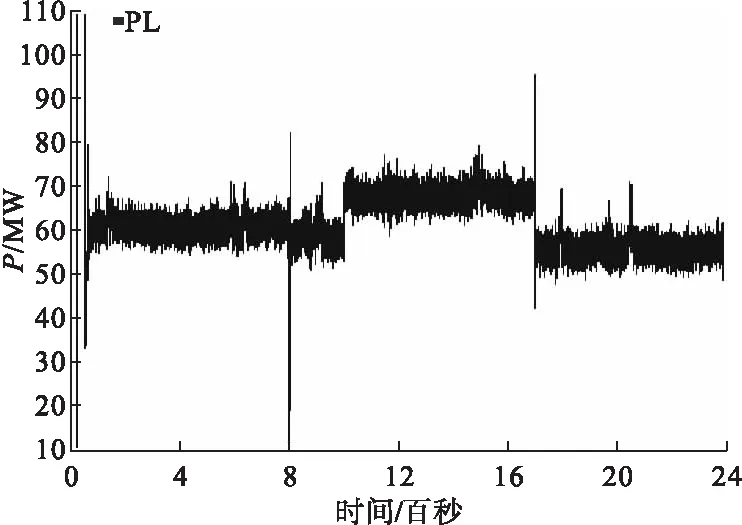


7 结论

