雷达信号脉内调制识别新方法

董志杰，王晓峰，田润澜

(1. 中国人民解放军95972部队，甘肃 酒泉 735018；2. 空军航空大学航空作战勤务学院，吉林 长春 130022)

0 引言

随着雷达技术的快速发展，雷达信号采取的调制方式越来越复杂，单纯提取传统的五大特征参数(即到达角、载频、到达时间、脉冲宽度及脉冲幅度)进行辐射源识别已经难以满足现代雷达对抗情报侦察的需要，而脉冲内部特征具有很强的稳定性与可分性。因此，在对截获雷达信号的分析中，脉冲内部特征识别(简称脉内识别)显得尤为重要。识别脉内调制特征可以提高信号分选的正确率、为雷达干扰提供引导、分析敌方雷达的技战术性能、雷达部署运用规律等。

关于雷达信号脉内调制类型的识别问题，在相关文献中已经提出了许多方法，并且随着雷达技术的不断发展，脉内调制类型识别技术也在不断更新。文献[1]利用信号在时频域的图像特征进行脉内识别，要求有先验数据，再通过一些分类器进行训练，不能进行信号的盲识别。文献[2]提出了基于正弦波抽取的自识别算法，文献[3]提出了基于核Fisher判别分析的自动识别算法。此外，还有基于纯数字特征的识别算法。其中，文献[4]提出了基于信号Holder系数的自动识别算法。总结以往算法存在的问题如下：第一，大多数算法识别的调制类型偏于简单，如只能识别LFM、BPSK等简单的脉内调制类型，无法识别MPSK等复杂信号，因此无法满足现实需求。第二，大部分算法的抗噪性能较低，当SNR在0dB以下时效果不理想，降低了算法的实用性。

针对上述算法存在的问题，提出了一种能够识别多种复杂调制信号的自动识别算法。文中首先对相位差分法进行了改进，提高了算法的抗噪性；然后针对STFT提取实际雷达信号存在特征不明显的问题，对STFT进行了改进，提高了时频精度与运算速度；最后，给出了基于层次决策的自动识别方法。仿真实验结果表明，提取的特征能够明显区分各型调制信号，在信噪比较低时具有较高的识别准确率。

1 调制特征提取

1.1 相位差分特征

设信号x(n)的无模糊相位为φ(n)，则信号瞬时频率估计值可以表示为：

(1)

(2)

式中，f(n)为信号瞬时频率真实值，fε为噪声产生的干扰频率。fε=Δε/(2π)，Δε为噪声引起的相位差。

对于频率调制信号，其瞬时频率变化较为平滑，因此可以采用多重相位差分降低噪声对瞬时频率提取的影响。对于相位编码信号，码元之间存在相位突变，其瞬时频率估计结果较为复杂，由相位差分得出的相位编码信号瞬时频率为：

=fc+fp+fε

(3)

式中，fc为归一化载频，fp=(θ(n)-θ(n-1))/(2π)为相位突变引起的归一化频率。不考虑Δε的影响，当码元内的相位无突变时，瞬时频率等于载频；而码元内相位发生突变时，瞬时频率会增加fp分量。因此，可以通过f(n)的变化情况得到相位跳变的信息。当信噪比较低时，受Δε的影响，直接计算相位已经难以准确提取信号的瞬时频率。因此，为了提高相位差分算法的抗噪性，需要进行适当改进，具体步骤如下：

步骤1：数字上变频。信号载频越高，相位差分时Δε对f(n)的影响越小。

步骤2：高阶相位差分。对相位序列p(n)进行M阶相位差分，再对相位差进行统计平均，通过相位差的积累来减小随机变量Δε对f(n)的影响，得到新的瞬时频率序列：

(4)

(5)

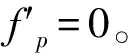
(6)

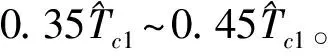
图1表明，直接相位差分受噪声影响严重，在噪声环境下无法有效描述信号的调制特征；改进相位差分实现了信号调制特征的准确描述，且与Morlet小波变换和Haar小波变换相比，具有更强的抑制噪声能力。这是由于小波的本质为带通滤波器，没有充分利用信号的相位信息，而改进的相位差分法充分利用相位信息进行平均处理，提高了抗噪性。

1.2 瞬时频率特征

信号的离散STFT为：

(7)

式中，M为窗的长度。遍历时频分布中每个时刻的最大值，可以得到信号的时频曲线。

中频信号采样频率fs=500 MHz，信号带宽B=5MHz，信号时宽T=100μs，则采样点数N=T/fs=50000。如果每次FFT点数Nf=256点，信号频率分辨率Δf=fs/Nf=1.95 MHz，则在信号频带内的分析点数ΔN=NfB/fs约为3点。因此，直接计算STFT效率很低，同时得到的有效频率变化范围很小，提取所得的瞬时频率曲线特征不明显，识别效果很不理想。

LFM信号进行STFT得到的时频图如图2所示。LFM信号的频率变化不明显，频率分辨率很低，不利于提取频率调制特征实现调制类型识别。

为了解决直接利用STFT特征不明显的问题，提出一种基于信号抽取的方式提高单次FFT的分辨率的改进STFT方法，该方法可以根据信号的时宽与带宽自适应地进行STFT。改进算法的实现过程分为以下几个步骤：

步骤2：降低采样率。对原采样序列每隔D点抽取一点，D的最大值为D=fs/B。为了防止抽取后点数过少，影响时频效果，设置最小抽取点数，并求出相应的D。如果D=1，表示不进行抽取，D>1，则进行抽取。抽取后得到新的采样序列，新的采样频率为fs/D。如果作相同长度的FFT，新采样序列的频率分辨率比原来提高了D倍。

步骤3：时频变换。对新采样序列进行STFT。为了得到与频率分辨率相对应的时间分辨率，可以设置相应的时间分辨单元。抽取后的数据越长，则自适应地增加FFT的滑动步长，确保时间分辨单元与频率分辨单元相对应。

LFM信号改进STFT如图3所示。信号参数同图2，抽取倍数为68，时频矩阵为256行736列。

对比图3与图2可知，改进STFT较直接STFT在性能上有了很大的提升，提高了时频变换的频率分辨率，可以清晰地反映出信号的频率变化规律，有利于进一步提取特征实现调制类型识别。并且改进STFT减小了计算量与存储空间，即减小整个信号处理过程时间和空间复杂度。

2 调制类型自动识别

2.1 相位编码识别

改进相位差分法对于BPSK和QPSK具有很好的检测效果，可以反映相位的跳变情况。理想状态下，在相位发生跳变时，BPSK信号的φ(n)∈{-π，π}；QPSK信号的φ(n)∈{-π，-π/2，π/2，π}；对于多相编码信号，不同码型对应不同的φ(n)，由于其跳变值是连续变化的，因此经相位差分后，跳变点的峰值各不相同，出现了一定的坡度。因此，可以根据相位跳变点来进一步细分调相信号。但受噪声等影响，跳变幅度有一定的起伏，需要设置相应的门限进行检测。再设置一对门限，记为H3、H4，且互为相反数，H3一般取值为110° ～130°。门限H1、H2用来检测低跳变幅度，H3、H4用来检测高跳变幅度。检测跳变峰值，且对峰值幅度p(i)进行量化，即有：

(8)

为了有效识别BPSK信号，统计|A(i)|为1与2的峰值序列p1(i)、p2(i)，相应序列的个数分别为L1、L2，设L=L1+L2。理论上，BPSK信号的L1应该为0，可以据此将BPSK信号从QPSK、多相编码信号区分开。但是当信噪比较低时，可能会出现伪峰，从而造成实际BPSK信号中L1>0。为了提高对BPSK信号的识别能力，设定当L1<δL时，则判为BPSK信号，δ一般取0.05～0.2。

2.2 频率调制识别

为了进行频率调制信号的类内识别，基于改进STFT提取信号的时频分布，然后利用时频曲线特征实现频率调制信号识别。LFM信号的瞬时频率具有线性特性，拟合时频曲线后计算其均方根误差。与其它频率调制信号相比，LFM信号的拟合误差很小。因此，设置拟合误差门限可以识别LFM信号。对于由传统STFT提取得出的调频曲线，线性拟合误差门限的取值为固定值，但对于本文提出的改进STFT，则需要一个自适应的误差门限，该门限与当前的抽取倍数及FFT的点数Nf有关。文中将线性拟合门限设为δffs/(DNf)，δf为误差系数。

为了实现NLFM信号与FSK信号的识别，提出一种基于瞬时频率的差分的识别方法。由于NLFM信号瞬时频率是连续变化，因此其瞬时频率的差分值变化平坦。而FSK信号的频率具有阶跃特性，其瞬时频率的差分值会出现多个尖峰，通过统计超过门限的尖峰个数，如果尖峰个数大于1，则识别为FSK信号。门限应该与信号的带宽有关，一般设为0.1B～0.2B。图4给出了两种调频信号瞬时频率的差分曲线，其中虚线部分为峰值门限，可以看出分类特征较为明显。

2.3 识别流程

依据前述对不同调制类型信号的特征提取和识别方法设计，可以总结出基于层次决策的雷达信号脉内调制类型识别算法，具体流程如图5所示。其中的关键步骤如下：

步骤1：信号预处理。首先计算截获信号的全序列平滑功率谱并进行滤波降噪，然后计算信号的时宽带宽积，从而实现非调制信号的识别。

步骤2：调制类型粗识别。计算步骤1输出调制信号的改进相位差分，提取信号的时相曲线，用时相曲线中是否包含突变特性实现相位编码信号与频率调制信号的识别。

步骤3：相位编码信号识别。进一步提取时相曲线特征，实现相位编码信号的具体调制类型识别。

步骤4：频率调制信号识别。首先通过改进STFT提取瞬时频率曲线，然后依据瞬时频率曲线特征实现频率调制信号的具体调制类型识别。

2.4 仿真实验分析

为了验证本文识别算法的有效性，进行如下仿真实验。仿真信号包括BPSK、QPSK、LFM、NLFM、FSK信号，信号采样频率为500MHz。BPSK、QPSK信号的码元序列随机产生，码元宽度在0.1～0.4 μs之间随机选取。NLFM信号为基于正切调制，时间副瓣控制因子为5。FSK信号采用载频个数为6的Costas型编码。噪声为加性高斯白噪声，SNR范围为-3～5dB。每类SNR每隔1dB进行500次蒙特卡洛仿真实验，结果如表1所示。

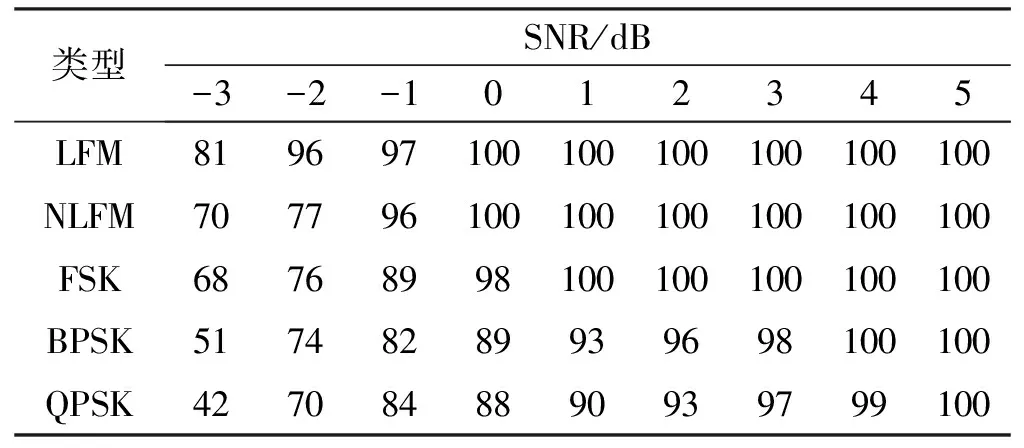
表1 不同SNR下的识别正确率 %

由表1可知，算法对LFM信号的识别率较高，这是因为LFM信号的线性频率特征易于识别；算法对低信噪比的QPSK、MPSK信号识别率较低，这是因为相位编码信号的相位跳变点提检测受噪声影响严重，造成识别错误。在SNR大于0dB时，算法对每种信号的识别正确率均能达到90%以上，且随着SNR增加，识别正确率也随之增加，当SNR达到4dB时，每种信号的识别正确率都可以达到100%。

设置相同的信号环境，将本文识别算法与几种常用的识别算法进行对比实验，对比算法包括相位差分法[5]、STFT时频法[6]与小波脊线法[7]，SNR为0 dB，实验结果如表2所示。

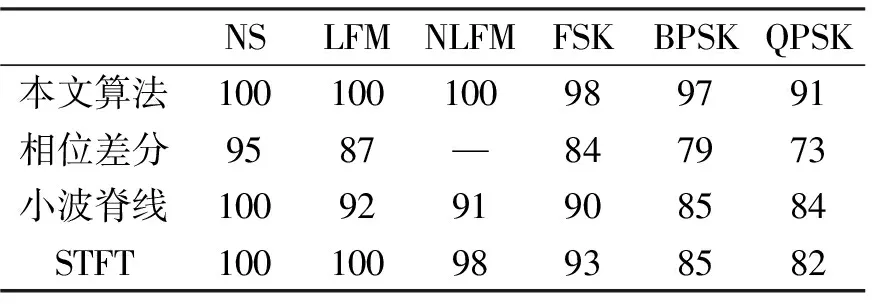
表2 几种识别算法的识别正确率 %

实验结果表明，与其他算法相比，本文算法具有较好的综合识别性能，识别准确率更高。这是因为相位差分法在提取瞬时频率时，易受噪声影响，从而导致算法对频率调制信号的识别率较低，同时无法识别NLFM等信号。小波脊线法由于提取信号的分类特征明显且抗噪性强，提升了整体的算法性能，但该方法提取的相位编码信号特征不明显，对相位编码信号识别准确率较低。STFT抗噪性较强，但是在处理长数据时需要耗费很长时间，且同样对相位编码信号的识别效果较差。

3 结束语

本文研究了雷达信号脉内调制类型识别问题，利用改进相位差分和改进STFT提取了雷达信号的调制特征，设计了基于层次决策的脉内调制类型自动识别算法。仿真实验结果表明，本文识别算法的分类特征明显，识别类型完整，抗噪性强，具有一定的工程应用价值。■

参考文献：

[1] Zhu J,Zhao Y,Tang J.Automatic recognition of radar signals based on time-frequency image character[C]∥Radar Conference 2013, IET International,IET,2013: 1-6.

[2] 胡国兵,华永平,刘渝.基于正弦波抽取的信号脉内调制识别算法[J].计算机工程,2010,36(13): 21-25.

[3] 周欣,吴瑛.核Fisher判别分析在数字信号分类中的应用[J].北京邮电大学学报,2011,34(1): 35-39.

[4] 王海华,沈晓峰.一种新的雷达辐射源信号脉内特征提取方法[J].系统工程与电子技术,2009, 31(4): 809-811.

[5] 黄知涛,周一宇,姜文利.基于相对无模糊相位重构的自动脉内调制特性分析[J].通信学报,2003, 24(4): 153-160.

[6] 于立涛,马洪光,艾名舜,等.基于STFT的雷达脉内调制信号类型识别[J].弹箭与制导学报,2006,26(2): 1198-1202.

[7] 隋莉莉,翟孝霏,陈涛,等.雷达信号有意调制的粗分类和细分类识别方法[J].现代雷达,2013, 35(2): 40-44.