一种基于TOA的单星无源定位新方法

徐学华，田 达

(中国航天科工集团8511研究所，江苏 南京 210007)

0 引言

随着电子信息技术的不断发展，电子侦察在现代战争中发挥着越来越重要的作用。低轨单星无源定位作为一种空间电子侦察技术手段，具有监视覆盖区域广、目标捕获能力强、安全隐蔽性好、系统相对简单等优点，受到各军事强国普遍重视。近年来小卫星技术的蓬勃发展，更促进了低轨单星电子侦察装备技术的快速进步。现有的低轨单星无源定位体制主要分为两大类[1]：一类是利用辐射源相对于卫星方位角度信息进行定位，如单星测向定位[2]和单星最小相位差定位[3]等。这类定位体制通常需要多个天线单元和接收通道，并且对卫星姿态测控、各天线单元及接收机通道之间的一致性要求都很高[4]，在微纳卫星平台应用可能受到较大限制。另一类是利用卫星与辐射源目标之间相对运动引起的多普勒效应来对辐射源位置进行估计，只要单个接收通道即可实现目标定位功能，大大降低了系统硬件复杂度，因而特别适合一些对侦察载荷的尺寸、质量、功耗有着严苛约束的应用场合。

文献[5]提出了利用卫星在不同的位置观测对应不同的多普勒频偏，联立求解多个频偏观测方程从而解出辐射源位置的方法。但这种定位体制需要Hz级甚至更高的频率测量精度，并且要求信号的载频在卫星观测期间保持固定不变，仅适用于持续时间相对较长的常规定频窄带通信信号，对短促的雷达脉冲信号往往难以适用[6]。文献[7]针对雷达信号侦察提出了仅测到达时间TOA的单星无源定位方法，通过测量的脉冲TOA序列，对目标相对运动的径向加速度进行估计，再根据径向加速度与相对位置之间的函数关系，联立求解多个不同时刻的观测方程解算出辐射源的位置。由于该方法加速度估计模型比较复杂，算法推导过程中做了一系列的近似，难免引入一定的模型误差，并且只能适用于脉冲重复周期(PRI)固定类型的简单雷达信号，因此难以适应实际环境中参数复杂多变的各种现代雷达信号。本文针对微纳卫星应用，提出了一种利用TOA观测序列提取雷达辐射源位置的新方法，该方法首先将侦察区域进行网格划分，然后根据卫星与地面的相对位置关系在每个网格点产生期望的TOA观测序列，并将其与实测TOA进行对比，选择与实测序列最接近的期望序列对应的网格点作为目标的位置估计，通过粗定位与精细定位相结合的处理方法得到最终结果。该方法具有系统简单、对卫星载荷要求不高、适应信号能力强等优点，理论分析和仿真计算表明，典型场景下的定位精度可达3 km，能够满足战术侦察应用需要。

1 问题模型

低轨卫星电子侦察场景下，辐射源与卫星的相对位置关系如图1所示。目标辐射信号经过空间传播到达卫星接收系统产生一定的距离延迟，而卫星与辐射源之间的相对运动导致距离延迟不断变化，因此接收端观测到的雷达脉冲序列与发射端相比，不但在时间上有ms量级的较大延时，而且脉冲间隔也有所改变(每1 km径向距离变化大致对应μs量级的脉冲间隔变化)。这种时域多普勒效应为卫星电子侦察系统利用TOA观测序列获取辐射源目标位置信息提供了可能[8]。

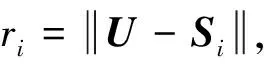
(1)

式中，c表示电磁波在空气中的传播速度，t0表示辐射源第一个脉冲的发射时间。对于固定重频的雷达信号，Tp即为雷达辐射源的PRI；对于具有复杂脉间变化样式的雷达信号，Tp可看作雷达脉冲时序电路的基本计数周期。Ni表示卫星在位置Si时接收到的辐射源脉冲与第一个脉冲所差的基本计数周期个数，以下简称计数索引值，这里不妨假定N1=0，即第一个脉冲对应的计数索引值为0，εi为卫星接收机到达时间的测量误差。

公式(1)给出的TOA观测模型中，参量t0，U，Tp，Ni均为未知量，对目标辐射源定位的问题就转化成对这些未知参量的联合估计问题。

为便于分析，进一步做以下假设和约定:1)电子侦察卫星的轨道高度为600～1000 km，雷达辐射源位于地球表面；2)卫星侦收期间，辐射源静止或做慢速运动，并且持续辐射脉冲信号，侦察系统能够以较高概率截获到目标信号；3)多目标问题已经通过信号分选处理得以解决，每个目标辐射的脉冲TOA序列可以单独分离出来进行定位处理，不考虑TOA观测序列中错误或丢失脉冲问题。此外假定雷达系统的PRI产生电路在卫星侦收观测期间具有较高的时钟稳定度(频率漂移或抖动变化引起的脉冲间隔变化小于1ns)，且基本计数周期Tp≥ 100ns，而侦察系统的TOA测量精度在10ns左右，或者比雷达系统PRI产生电路的基本计数周期小约1个数量级。上述假设在实际应用中大多数情况下都能得到满足。

2 定位算法

在侦收信号的过程中，卫星处于不同位置(S1,S2,…,Sk)时，对应得到的脉冲到达时间为(TOA1,TOA2,…,TOAk)，将公式(1)写成方程组的形式，如式(2)所示。

(2)

在上述方程组的所有待估参量中，Tp、Ni与目标位置无关，若能从TOA观测序列中先估计出Tp及Ni，则问题就可以简化为对三维位置变量U及辅助变量t0的联合求解，原则上只需联立4个方程即可解出目标位置。

2.1 计数周期Tp的估计

对于脉冲重频固定的雷达信号，采用传统的雷达脉冲重复周期估计方法即可得到Tp。下面主要讨论复杂脉冲间隔样式的计数周期估计。

需要特别说明的是，虽然上述方法不一定能够得到真正的基本计数周期Tp(可能是其整数倍),但Tp与计数索引值Ni相互耦合，只要Tp与Ni的乘积满足数据拟合关系，就不会影响对目标辐射源位置的估计。

2.2 计数索引值Ni的估计

(3)

式中，Δε=εi-ε1，Δri=ri-r1表示径向距离差。在对Ni进行计算时，需要注意径向距离变化不能过大，否则可能导致Ni估计错误。通常卫星位置的选取应满足以下条件：

简简单单的52个字，却将大茉莉的情感与内蕴展现无余。细细品读，内中声韵跃然纸上。作为作曲，我为能够有此好词而欢欣、雀跃。

(4)

2.3 目标位置估计

对于非线性方程组，直接求解可能较为困难。牛顿迭代方法较为常见，但初值选取不好可能导致算法不收敛，这里采用性能更加稳健的网格搜索方式进行问题求解。首先将侦察区域进行网格划分，得到一系列网格点{Zp,q}，对每个网格点Zp,q借助TOA1反演算出雷达的发射时间t0(p,q)：

(5)

根据网格点Zp,q与卫星在不同位置(S1,S2,…,Sk)的相互关系，可以计算得到期望的脉冲到达时间序列toai(p,q)：

(6)

将期望toai(p,q)与实测TOAi相减得到误差序列：ei(p,q)=toai(p,q)-TOAi(i=1,2,…,k),并对误差序列进行平方统计，得到每个网格点的统计量，在此基础上构造整个网格区域内的TOA拟合误差信息场{gp,q}：

(7)

gp,q反映了网格点Zp,q对应的期望TOA序列与实测TOA序列的相似程度，当网格点接近目标真实位置时，gp,q应当接近最大值。通过搜索拟合误差信息场{gp,q}的最大值，即可得到目标位置估计值。

2.4 算法步骤总结

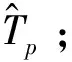
2) 选择相应的卫星位置(S1,S2,…,Sk)，通常选择卫星位置间隔1s以上，所选取的卫星位置个数不少于4个，计算其对应的计数索引值(N1,N2,…,Nk)；

3 定位精度CRLB推导

假定TOA测量误差为一系列独立同分布的零均值高斯随机变量，误差矢量的协方差矩阵为Q，则TOA观测序列t的似然函数为：

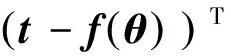
(8)

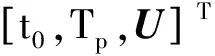
CRLB计算公式如下[9]：

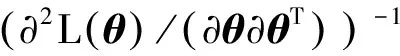
(9)

式中，

地面约束条件下的CRLB为[10]：

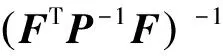
(10)

式中，F为地面约束方程的梯度矢量，如果满足UTU=R2的地球正球面约束，可以得到F=UT。

4 算法应用分析

4.1 侦收时间

这里侦收时间会涉及两方面，一是卫星在某一位置时的侦收窗口，该窗口的侦收时间主要与基本计数周期Tp的估计相关。例如对于重频固定的雷达脉冲信号，侦收100个左右的脉冲即可得到脉冲重复周期的估计值。但是对于一些重频捷变的雷达信号，需要侦收的窗口可能要更长一点。二是卫星为了得到定位结果所需总的侦收时间，总的侦收时间越长，径向距离变化越大，所得到的定位结果更好。从仿真结果来看，卫星总的侦收时间不应小于4s。

4.2 搜索算法

网格搜索法最大的弊端是遍历所有网格点时计算量很大。为了降低网格搜索的计算量，可以采用多级网格搜索的方法，兼顾大网格划分计算量小和小网格划分定位精度高的优势。同时考虑到镜像模糊点与目标真实位置的对称性，可以先对卫星运动方向的左侧或右侧进行搜索，得到粗位置解时，再利用对称性得到另一侧的粗位置解，最后同时对左右两侧的粗位置解附近区域进行细网格划分，搜索得到目标位置与镜像点位置。这种引导搜索的方式不仅减少了网格搜索的代价，同时也避免了在进行遍历搜索时，因网格划分的离散性导致峰值搜索的结果不是目标的真实位置，而是镜像点位置。

4.3 算法适应性

文中提到TOA测量精度为10ns，这一指标的提出主要是依据基本计数时钟的周期。为了对基本计数周期得到正确估计，TOA的测量精度应该比基本计数周期高一个数量级。同时由于该算法可以容忍基本计数周期模糊估计，故在实际应用中，TOA测量精度可以相对放宽。比如对于重频固定的雷达信号，重复周期范围在0.2～20ms，TOA的测量精度可以放宽到50ns。对于一些重频捷变的雷达信号，若重复周期的步进值大于500ns，TOA的测量精度可以放宽到30ns。同时该算法对平台的要求比较低，只需要单个接收通道，能够适应微小卫星的发展需求。

5 仿真分析

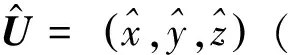
定位精度与卫星总的观察时间相关，卫星运动的时间越长，所获得的信息量越多，目标相对卫星的径向距离变化越明显，故更便于凸显目标位置的特征信息。下面针对卫星在不同观察时间下所获得的定位结果进行分析。

如图3所示，卫星总的观察时间为2s(每个卫星位置间隔0.5s)，时间比较短，拟合误差信息场分布图中有许多次峰出现。由图4可知，卫星总的观察时间为4s(每个卫星位置间隔1s)，拟合误差信息场分布图中次峰下降，峰值明显。图5给出了在不同的卫星观察时间下的目标定位精度。随着卫星观察时间的增加，定位误差得到明显改善。并且在4s内就可以达到3km的定位精度，收敛速度快。

如图4所示，拟合误差信息场分布图中存在一个镜像模糊点，该镜像点是单星利用多普勒效应进行定位的通病，原因是卫星侦收区域的多普勒速度分布是关于卫星航迹对称的。目前，工程上剔除镜像点的方法主要是增加测向信息，但这并不符合微小卫星所提倡的单通道需求。考虑到微小卫星多星联网的特点，即未来发展的微小卫星同一轨道上会同时分布多颗卫星，并且具有多个轨道面，从而实现对目标区域长时间的侦察。由于同一轨道面内的卫星经过同一区域时，星下点位置并不是完全相同，这将出现同一个辐射源在同一轨道面不同卫星侦察的情况下，镜像点出现的位置不同，如图6所示，故可以通过多星组网的方式达到解镜像模糊的目的。

6 结束语

本文提出了一种基于TOA观测序列的单星快速侦察定位方法，采用多级网格搜索的策略获取目标位置的最优解，减少了计算量。该方法对卫星载荷的要求不高，只需要单个天线和通道就可以满足定位的需求，适合微小卫星平台的应用，通过多星组网的方式可以实现镜像点的剔除。仿真结果表明，在TOA测量误差较小的情况下定位精度能够满足战术侦察应用的需要。■

参考文献：

[1] 郭福成. 空间电子侦察定位原理[M]. 北京：国防工业出版社, 2012：15-20.

[2] 郭福成. 基于WGS-84地球模型的单星测向定位方法

[J]. 宇航学报, 2011, 32(5):1179-1183.

[3] 陆安南，杨小牛. 最小相位误差单星无源定位法[J]. 上海航天, 2007, 24(3):6-9.

[4] 李文华，陆安南. 星载测向定位滤波算法研究[J]. 计算机仿真, 2010, 27(5):57-61.

[5] 黄振，陆建华. 天基无源定位与现代小卫星技术[J]. 装备指挥技术学院学报, 2003, 14(3):24-29.

[6] 龙宁. 单星无源定位原理及精度分析[J]. 电讯技术，2011，51(6)：17-20.

[7] 徐义，郭福成，冯道旺. 一种单星仅测TOA无源定位方法[J]. 宇航学报, 2010, 31(2):502-508.

[8] Liu Yang，Guo Fucheng，Yang Le. Source localization using a moving receiver and noisy TOA measurements[J].Signal Processing，2016，119：185-189.

[9] Steven M. Kay statistical signal processing estimation theory[M].New Jersey:Prentice Hall PTR,1993:27-50.

[10] Jagannathan AK,Rao BD.Cramer-Rao lower bound for constrained complex parameters[J].IEEE Signal Processing Letters,2004，11(11)：875-878.