应用STK工具的BDS仿真分析

吕春东，王 佳，闫 飞

(北京林业大学 精准林业北京市重点实验室/测绘与3S技术中心，北京 100083)

0 引言

21世纪，随着卫星导航技术不断发展和进步，人类社会对于卫星导航定位的需求也越来越大。我国的北斗卫星导航系统(BeiDou navigation satellite system，BDS)和美国的全球定位系统(global positioning system，GPS)、俄罗斯的格洛纳斯卫星导航系统(global navigation satellite system，GLONASS)同为目前世界三大成熟的全球卫星导航系统。2012-12-27，我国发布了BDS空间信号接口控制文件(又称 ICD文件)，标志着我国的BDS初步建成，并正式对亚太地区提供服务；自此我国BDS完成了三步走发展战略的第二步[1]。目前我国的BDS还正在加紧组网建设中，计划于2020年全面建成，届时可面对全球提供定位、授时、测速等服务。

我国对于BDS性能的分析研究主要以国防科大、武大、北航和南航等我国大学科研机构为主。目前，文献[2]研究了覆盖星与BDS星座系统性能之间的关系；文献[3]详细仿真分析研究了BDS卫星星座的组网设计布局；文献[4]在研究确定了几何精度衰减因子(geometric dilution of precision，GDOP)的标准后，计算了在BDS下各地面站GDOP的变化。这些科学研究已经逐步检验了BDS的可用性与可行性，分析了BDS星座覆盖和定位精度等。

本文在前人研究的基础上进一步对BDS卫星的可见性、覆盖性和定位精度进行分析，同时对近几年新发射的卫星进行仿真，以增加分析结果的稳定性与可靠性。

1 BDS、STK概述及仿真数据介绍

BDS是我国目前已经在应用并还在继续建设中的全球覆盖的卫星导航系统。该系统建设目标是：建成独立自主、开放兼容、技术先进、稳定可靠的覆盖全球的BDS，促进卫星导航产业链形成，形成完善的国家卫星导航应用产业支撑、推广和保障体系，推动卫星导航在国民经济社会各行业的广泛应用。BDS的3个部分分别为用户段、地面段和空间段，空间段包括5颗静止轨道卫星和30颗非静止轨道卫星，地面段分为监测站、主控站和注入站等，用户端则包括BDS用户终端以及与其他卫星导航定位系统相兼容的终端[5]。

BDS由地球静止轨道(geostationary Earth orbit，GEO)、 中圆地球轨道(medium Earth orbit，MEO)和倾斜地球同步轨道(inclined geo-synchronous orbits，IGSO)组成。GEO的轨道高度为35 786 km，定点位置为58.75°E、80°E、110.5°E、140°E、160°E；MEO的轨道高度为21 528 km，轨道倾角为55°，运行在3个轨道面上，各轨道面之间相隔120°均匀分布；IGSO的轨道高度为35 786 km，轨道倾角为55°。截止至2017年3月，BDS在西昌发射出23颗卫星，20颗组网并已经在使用，分别为6颗GEO、8颗IGSO和6颗MEO。

卫星工具箱(satellite tool kit，STK)是一款由美国Analytical Graphics公司开发研制，广泛应用于航天领域的分析工具，其主要功能[6-9]为：

1)分析能力，可以把卫星在任何时刻的姿态和位置快速计算出来，同时计算空间对象与海、陆、空之间的相互关系；

2)生成轨道，可以快速生成卫星轨道，也可通过输入卫星轨道的参数创建；

3)卫星数据库，可以在卫星数据库中包含的大部分卫星数据中直接添加卫星；

4)可见性分析，以报告形式显示出计算的空间各对象间访问时间及结点；

5)遥感器分析，在航天器或者地面站上附加遥感器，可以精确计算其可见性；

6)姿态分析，可定义标准姿态，也可以自己输入姿态文件，能分析计算姿态运动对其他参数的影响；

7)可视化的计算结果，可同时打开多个显示窗口，显示出二维、三维图形以及不同投影和坐标的图形；

8)全面的数据报告，对于各种不同分析的结果，可以输出全面的报告。

北美防空联合司令部(North American Aerospace Defense Command，NORAD)开发的双行的轨道预报模型是一种应用于航天器自主导航和中长期的轨道预报的解析轨道预报模型，该模型具有较高的精度。NORAD开发了一种卫星星历又称两行轨道数据(two-line orbital element，TLE)传输开普勒轨道根数来建立模型[10]。TLE数据表明了空间目标的位置和速度，TLE包含2行数据，采用文本格式记录，其中包含数字0～9，大写的英文字母A～Z，正负号、空格和句号。一旦太空中有空间目标进入，就会被北美防空联合司令部的卫星星历的编号目录记入，并且在其运行过程中会一直被记录。目前TLE轨道根数技术操作已经十分成熟，其应用广泛，包括太空垃圾的轨道设计、定位、预测和跟踪军事，还包括航天器、交通、天文以及卫星导航定位技术等等。飞行体的时间、速度、坐标和岗位等参数都能通过TLE数据来确定，且精度很高[11]。本文使用的TLE数据从北美防空司令部网站上下载。

2 BDS星座设计及建立

目前全球大部分卫星导航定位系统都采用的是Walker星座布局。Walker星座是一组圆轨道卫星，它们具有同样的运行轨道周期和同样的倾角，记为Walker T/P/F，均匀分布在各个轨道上的卫星的间距都是相等的，各个轨道面之间的升交点经度之间的距离也是相隔相同的角度平均分布，因此T(卫星的数目)=s(相同轨道面的卫星的数目)×P(轨道面的数目)。2个轨道相邻的卫星的相对相位是通过相位参数F来计算，F表示在最东边的卫星到在最西边的卫星这2颗卫星轨道间的“缝隙”个数(360°/T)，F为0到P-1的整数。BDS的Walker星座为27/3/1，回归的周期为7 d(13圈)，相位从Walker27/3/1星座中选取，第一轨道面升交点的赤经为0°[12]。

本文主要设计建立目前已公布的20颗正在使用的卫星，即6颗MEO卫星+6颗GEO卫星+8颗IGSO卫星，其星座仿真过程如下：在STK软件中建立20颗卫星，分别调出其属性表并将其Propagator选为SGP4模型，将卫星TLE数据导入，即可显示BDS卫星的三维图形(如图1所示)和二维图形(如图2所示)。

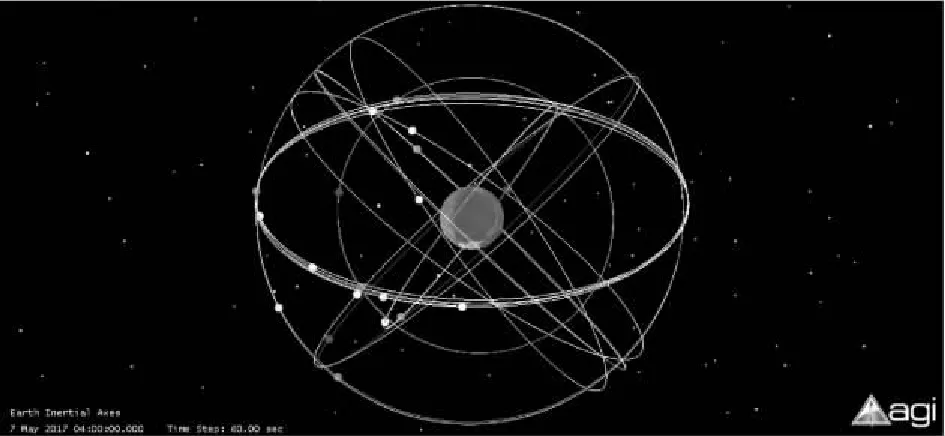
图1 BDS卫星三维图形

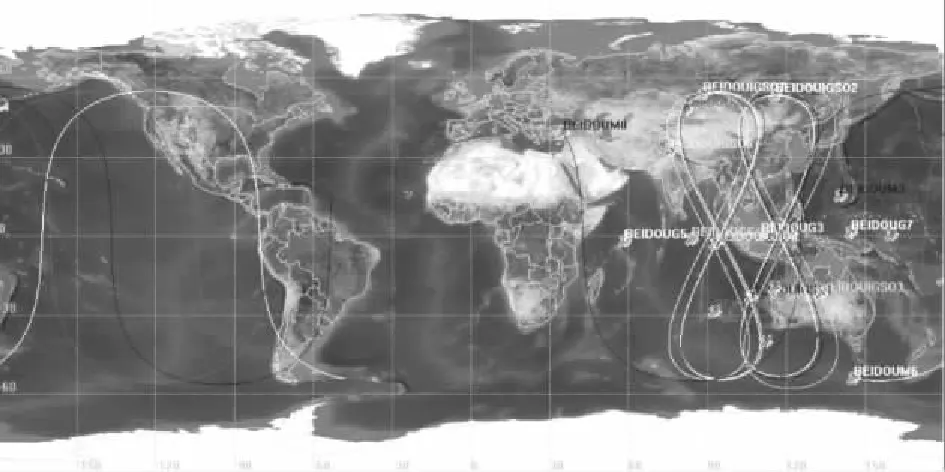
图2 BDS卫星二维图形

3 BDS的可见性与覆盖性分析

本文研究BDS对中国地区的可见性与覆盖性，所以对地面站的选取有一定的要求，要求其地理位置和社会环境都具有一定的代表性。出于以上考虑，本文选取首都北京作为中国社会环境的代表城市，地理位置上选取中国北部城市伊春、南部城市三亚、中部城市兰州、西部城市喀什和东部城市上海，这5个城市在地理位置上包含了中国的东西南北中，充分覆盖了中国地区。总体来说，这6座城市作为地面站能充分代表中国的地理位置和社会环境，对本文分析提供有效依据[13-14]。

STK包含许多用于任务分析的模块，包括基础分析模块和专业分析模块。基础分析模块包括可见性计算(Access)和层访问(Deck Access)等工具，其中本文主要选用可见性计算，其可以计算对象之间的可视状态，通过Access工具，确定一个对象可以访问或看到另一个对象的时间间隔，还可以对指定对象间的访问加以限制，来确定是否构成了有效的访问，其分析结果说明了在一天内不同卫星对不同地面站的可见时间段。本文通过Access工具来分析单颗卫星对地面站的可见性。STK专业分析模块包括覆盖(Coverage)、通信(Communications)等工具[15]，其中本文主要选用Coverage，Coverage工具主要用于考虑在各种可见性约束条件下的一个或多个覆盖资源对区域范围的覆盖性能分析，其分析结果说明了在1 d之内不同地面站在不同时刻可接收到的卫星数目。本文通过Coverage工具来分析BDS对地面站的覆盖性。

通过卫星对地面站的可见性与覆盖性分析，以北京地面站为代表，其可见性分析及覆盖性分析结果分别如图3和图4所示。

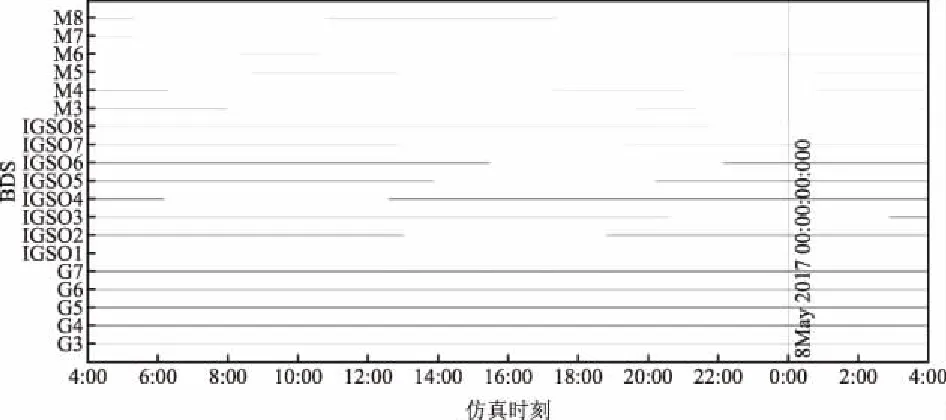
图3 北京观测站2017-05-08的卫星可视情况

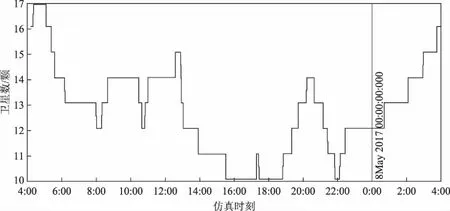
图4 北京观测站卫星可见数

由图3可知每颗卫星在1 d内哪些时间段可见；由图4可知在一个时刻覆盖此观测站的卫星颗数。根据卫星对地面站的可见性与覆盖性分析结果，将北京地面站的数据与其他5个地面站的观测数据进行整理，如表1和表2所示：其中表1数据为图1中不间断的线段数，表明了可全天不间断覆盖观测站的卫星数目；表2为不同时刻卫星数的算术平均数，表明了在某一时刻能够覆盖观测站的卫星数目。

表1 地面站全天可见卫星数汇总(可见性分析)

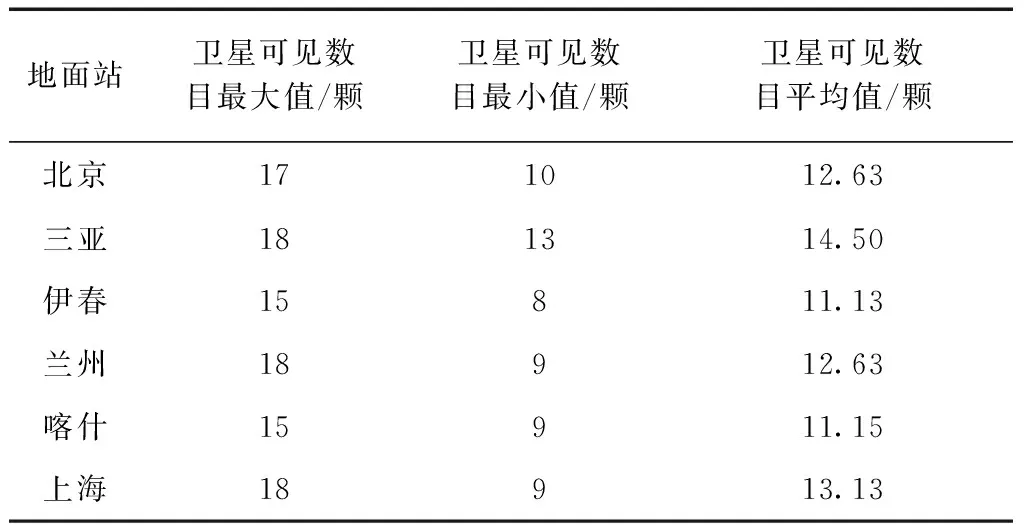
表2 地面站卫星可见数目一览表(覆盖性分析)

由表1可知：当前星座下，北京观测站全天可见卫星数为5颗，三亚观测站全天可见卫星数为13颗，伊春观测站全天可见卫星数为4颗，兰州观测站全天可见卫星数为5颗，喀什观测站全天可见卫星数为4颗，上海观测站全天可见卫星数为5颗；由此可见低纬度地区全天可见卫星数目较多，高纬度地区全天可见卫星数目相对较少，不同地区的全天可见的卫星数会伴随着纬度的增大而减少。由表2可知：从不同观测站卫星可见数目来看，BDS在北京、三亚、伊春、喀什和上海的卫星可见数目都保证在8颗以上，表明BDS在我国覆盖全面；BDS在6个城市可见卫星的数量和城市的分布有一定关系，因而纬度越高，覆盖性相对较差，纬度越低，覆盖性越好。

4 BDS定位精度分析

对于大部分的BDS的使用者来说，他们最关心的是位置的精度和在确定的精度下的测量数据的可靠性。对于BDS的定位功能，其精度主要受2个因素的影响：一是所监测的卫星在空间里的几何分布；二是观测量的精度。位置精度为

(1)

式中：Accuracy为位置精度；UERE为用户等效距离误差；DOP为精度衰减因子，其结果越小，用户的定位精度越高。本文主要通过STK仿真研究DOP对位置精度的影响[16]。

在导航学中，通常以精度衰减因子(dilution of precision，DOP)这个概念来表示误差被放大的倍数，其反映了卫星在空间中的几何分布，是用来表示星座的大小和星座的轨道参数的一个函数；DOP作为一个用来评估位置精度质量的参数，其影响是非常大的。可见的卫星个数、卫星星座的位置、方位及卫星高度这几个数据可以决定DOP的测量结果，DOP能反映出地面站和卫星之间的的定位精度。大部分情况下，可见卫星之间的夹角与DOP的值成反比，即夹角大则DOP值就小，表明测量结果好。DOP值小就是说卫星的星座几何构型很好，观测环境和观测条件也好。所以，想要测量结果具有高的可靠程度，其DOP结果就要小。DOP因子通常包括：平面位置精度衰减因子(horizontal dilution of precision，HDOP)、高程精度衰减因子(vertical dilution of precision，VDOP)、空间位置精度衰减因子(position dilution of precision，PDOP)、接收机钟差精度衰减因子(time dilution of precision，TDOP)和几何精度衰减因子(geometric dilution of precision，GDOP)[17]。在这几个DOP中，几何精度衰减因子GDOP描述的是卫星的几何形态对三维的空间位置和时间测量的影响，是关于空间几何形态最完整的表达[18-21]；因此本文选择GDOP代表BDS的定位精度程度。

通过STK的Coverage模块，能够分析出单个卫星或者星座对象的全局或者区域覆盖的问题。在使用其覆盖的功能时，STK能够计算出各种不同的结果并输出报告，能同时仿真出覆盖的变化，并且还会确定访问约束，避免误差的出现。通过上文讨论，本文选取GDOP精度因子来对BDS的定位精度进行分析。利用STK软件覆盖品质参数FOM工具，选取GDOP参数，分别以北京、三亚、伊春、兰州、喀什和上海为覆盖对象，以目前BDS的20个卫星为覆盖资源，对BDS的定位精度进行分析，其中北京地面站的GDOP值变化如图5所示，将其与其他5个地面站的观测结果进行整理，如表3所示。

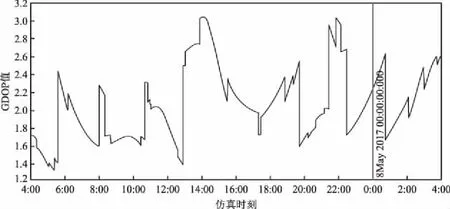
图5 北京观测站GDOP值变化

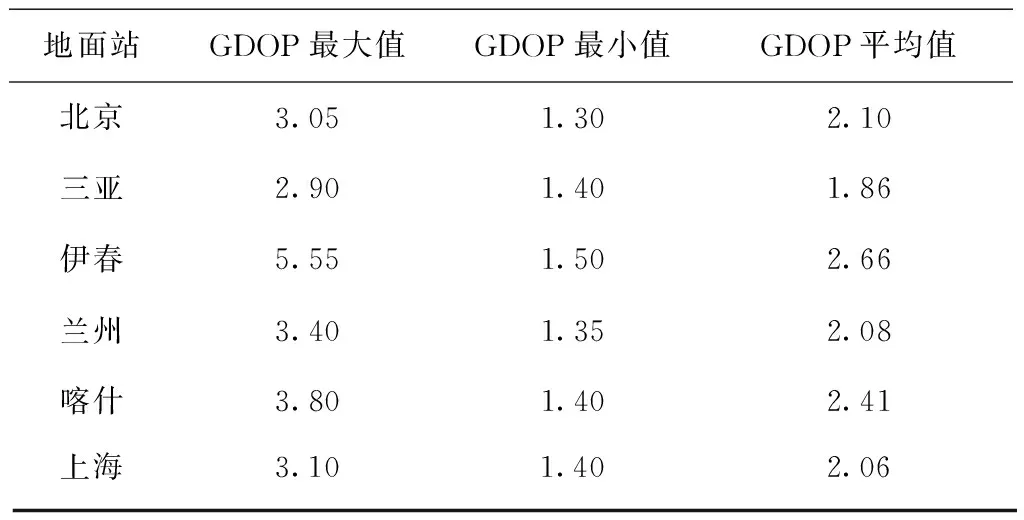
地面站GDOP最大值GDOP最小值GDOP平均值北京3.051.302.10三亚2.901.401.86伊春5.551.502.66兰州3.401.352.08喀什3.801.402.41上海3.101.402.06

由表3可知BDS在北京、三亚、伊春、兰州、喀什和上海的GDOP值都控制在6以下，能够达到10左右的设计要求，BDS在我国定位精度达到良好以上。结合表1和表2来看，BDS系统在6个地面站可见性、对6个地面站的覆盖性影响到了GDOP值。由此推知：BDS的定位精度与地面站纬度也有一定关系，即：纬度越高，卫星可见数越少，其定位精度相对较差；纬度越低，卫星可见数越多，其定位精度越高。但总体来讲，从各观测站的GDOP值变化图可以看出，GDOP值的起伏波动很大，可知BDS定位的稳定性不够好，还需进一步加强。

5 结束语

本文通过分析BDS的构成，并对基础软件工具STK和BDS仿真过程中用到的TLE数据进行介绍，概述了BDS仿真的星座设计以及地面站的建立方法和流程。在仿真分析中，本文选用STK软件模拟BDS的星座进行BDS的卫星可见性与覆盖性分析以及定位精度分析，得到以下结论：

当前的BDS星座在中国地区的可见性良好，在低纬度地区全天覆盖卫星数能够保持在10颗左右，在高纬度地区全天覆盖卫星数能够保持在4颗左右；低纬度地区卫星可见数最少保持在11颗左右，高纬度地区卫星可见数最少保持在8颗左右，也能够达到对定位的最低保障。从对GDOP的分析可知，BDS在中国范围内具有非常好的覆盖品质，大部分地区的定位精度都很高，但稳定性一般。在BDS不断建成的过程中，其定位的准确性及稳定性将会越来越好。

总体来说，BDS是一种未来能覆盖全球并具有高精度的定位导航功能的卫星导航系统，能够为使用者提供高精度的信息服务。BDS现在还处于建设过程中，本文使用STK软件的许多分析功能对BDS进行了仿真分析，但是其仿真的精度还需要在系统完全建成后才能够更加准确，并需要在建成使用后得到实践的检验。本文的工作对于进一步应用和建设BDS、BDS建设项目过程中其他的理论分析和项目拓展有一定的参考意义。

[1] 曹翔.基于STK的北斗二代星座仿真及GDOP值分析[J].科技视界，2015(35)：13-15.

[2] 帅平，曲广吉，陈忠贵.区域导航星座分析设计研究[J].空间科学学报，2006，26(4)：268-276.

[3] 妥艳君，刘云，李艳.LEO/MEO星座组网设计与分析[J].电子科技大学学报，2010，39(1)：50-54.

[4] 陈岩，陈晖，丁前军.“北斗二号”卫星导航系统覆盖仿真分析[J].通信技术，2009，42(6)：171-173.

[5] 丁锁妹.北斗卫星导航系统观测数据的可用性分析[D].大连：大连理工大学，2014.

[6] 张大力.基于STK软件的北斗导航卫星轨道模拟[J].测绘工程，2015，24(7)：10-19.

[7] 秦大国，陈星.STK及其在卫星组网仿真演示中的应用研究[J].指挥技术学院学报，2001，12(4)：66-69.

[8] 于燕婷.STK软件及其在卫星导航系统中的应用[J].舰船电子工程，2016，36(7)：62-65.

[9] 郭斐，张小红，于兴旺，等.基于STK软件的GALILEO系统仿真与分析[J].测绘信息与工程，2009，34(1)：3-6.

[10] 车通宇，杨力，张传定，等.SDP4模型用于北斗导航卫星轨道预报的精度分析[J].测绘地理信息，2017，42(2)：12-16.

[11] 戴仔强，邢芳.基于TLE和SDP4模型的GPS+北斗混合系统DOP值模拟[J].指挥信息系统与技术，2015，6(4)：68-72.

[12] 施闯，赵齐乐，李敏，等.北斗卫星导航系统的精密定轨与定位研究[J].中国科学：地球科学，2012，42(6)：854-861.

[13] 张龙平，党亚民，许长辉，等.地面测控站分布对北斗卫星精密定轨的影响[J].测绘科学，2015，40(12)：68-72，90.

[14] 王鹏旭，吕志伟.北斗混合星座DOP值与定位性能分析[J].全球定位系统，2016，41(6)：6-10.

[15] 丁溯泉，张波，刘世勇，等.STK使用技巧及载人航天工程应用[M].北京：国防工业出版社，2016：83-107.

[16] 范龙，柴洪洲.北斗二代卫星导航系统定位精度分析方法研究[J].海洋测绘，2009，29(1)：25-27，45.

[17] 雷浩，廉保旺，何伟，等.STK北斗二代卫星导航系统在亚太地区DOP值仿真分析[J].火力与指挥控制，2014，39(6)：52-55.

[18] 李建文，李作虎，周巍，等.卫星导航中几何精度衰减因子最小值分析及应用[J].测绘学报，2011，40(增刊)：87-94.

[19] 曹昌龙.北斗二代定位算法优化设计与应用[D].北京：中国科学技术大学，2014.

[20] 王尔申，岳孝东，何赫，等.“北斗”卫星导航系统仿真与全球覆盖分析[J].电讯技术，2016，56(8)：918-922.

[21] 肖乐杰，孙付平，李亚萍，等.IGSO/GEO卫星对北斗系统导航性能的贡献分析[J].全球定位系统，2016，41(3)：16-20.