间接DGM(1,1)模型在基坑沉降预测中的应用

王 岩，黄张裕，张玉爽，艾合塔木•依米尼亚孜，王文利

（1. 河海大学 地球科学与工程学院，江苏 南京 211100）

一个新鲜事物自诞生以来总会不断被发掘、传播和推广，灰色系统理论亦是如此。“小样本”、“贫信息”贯穿整个灰色系统理论[1-3]。部分信息已知、部分信息未知是灰色理论的典型特征[4-5]。其通过累加生成的方法，对原始数据进行加工，使数据中隐藏的信息得以显示[6-7]。许多新模型应运而生，灰色预测模型已 由 GM(1,1)发 展 到 DGM(1,1)、GM(2,1)、DGM(2,1)、GOM(1,1)、 新 陈 代 谢GM(1,1)等[8-13]。 本 文 采 用GM(1,1)、DGM(1,1)、间接DGM(1,1)3种模型对基坑沉降进行预测。

DGM(1,1)模型是GM(1,1)的离散形式，对于不同的数据列，其预测精度有较大差别，有时甚至完全失真。对何种类型数据列的预测精度高，何种类型数据列的预测精度低，是使用该模型的关键。近似非齐次指数增长序列和近似齐次指数增长序列是仅相差一个常数项的两种数据列，但使用DGM(1,1)模型对这两种数据列进行预测时，精度有较大差别，后者要高于前者[14]；而现实中近似非齐次增长序列比近似齐次指数增长序列要普遍得多，两种数据列的转化是提高预测精度的关键。将基于近似非齐次指数增长序列的灰色预测模型称为间接DGM(1,1)模型。它是DGM(1,1)的衍生模型，旨在进行两种数据列（近似齐次、近似非齐次）之间的转化。GM(1,1)、DGM(1,1)和间接DGM(1,1)模型都是变形预测的有效模型，本文采用这3种模型对基坑沉降进行预测，并对预测精度进行了比较。结果表明，间接DGM(1,1)预测曲线十分接近实测值曲线，随着周期的增长，预测值并没有像另两种模型那样较大幅度地偏离实测值，且在8～10周期预测效果最好；它对短中期和长期预测均适用，弥补了另两种模型不能进行长期预测的缺憾。

1 GM(1,1)模型与DGM(1,1)模型

1.1 GM(1,1)模型

对序列进行运算为运算得到的序列，其中n。对序列x1建立微分方程：

以最小二乘法为约束条件，求得[a b]T=(BTB)-1BTYN，其中对式（1）求解，得到：

累减生成后的还原数据为：

判断灰色模型精度等级的C、P值如表1所示。其中，模型精度等级=max{P所在级别,C所在级别}。C越小效果越好，P越大效果越好。

表1 模型精度等级

1.2 DGM(1,1)模型

将称为离散灰色模型，即DGM(1,1)模型。对序列进行运算为运算得到的序列，其中

令为参数列，由最小二乘法得其结果其中由于故预测模型为：

还原值为：

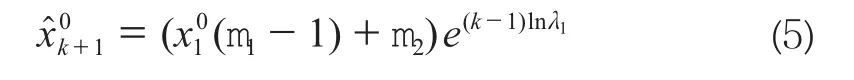
2 间接DGM(1,1)模型

对序列进行运算，得到序列其中为近似非齐次指数增长序列，则序列y0为近似非负齐次指数增长序列，实现了两种序列的转化，这是建立间接DGM(1,1)模型的关键。序列其中k=1,2,…,n。

令m = [ m1m2]T为参数列，由最小二乘法得到：其中由式（4）可知，

作累减还原可得：

化简得到：

式（6）为序列y0的DGM(1,1)预测模型。由于故进而得出序列x0的间接DGM(1,1)预测模型为：

3 实例分析

对某基坑进行沉降监测，基坑周边为居民楼，基坑长45.7 m，宽13.7 m，最大开挖深度为11 m，共布设20个沉降监测点，监测11个周期，选取任一点进行分析，其11个周期的累计沉降量（实测值）、预测值和残差如表2所示。通过计算得到3种模型的P、C值和中误差，见表3。

表2 3种模型的预测值与残差/mm

表3 3种模型的P、C值和中误差

由表2可知，累计沉降量满足近似非齐次指数增长，适合建立间接DGM(1,1)模型。由表3可知，间接DGM(1,1)的C值比另两种模型小得多，所以间接DGM(1,1)的模型精度要高于另两种模型。就中误差而言，间接DGM(1,1)要远低于另两种模型，且不在同一 个量级上，说明间接DGM(1,1)的预测效果比GM(1,1)、DGM(1,1)要好。3种模型残差曲线如图1所示。预测曲线和实测曲线见图2。

图1 3种模型残差图

从图1可以发现，间接DGM(1,1)的残差值上下浮动较小，较稳定，没有出现大幅度波动，增加缓慢近似一条水平线，实测值与预测值非常接近，最大值不超过0.2 mm，即使在后期，也没有出现随周期增加而快速增长的情况，始终控制在0.1 mm之内，短、中、长周期都取得了较好的预测效果。其他两种模型的残差值在7周期以前出现了下降，具有较好的短中期预测效果，但在7周期以后，残差值随周期增加而不断增大，且增长幅度较大，说明这两种模型不适合长期预测。

图2 3种模型预测曲线和实测曲线

从图2可以看出，GM(1,1)和DGM(1,1)的预测曲线除在6～8周期与实测值曲线偏离较小外，其余周期均与实测值偏离较大，7周期后与实测值偏离越来越大，说明这两种模型仅适合短中期预测，不适合长期预测；而间接DGM(1,1)预测曲线十分接近实测值曲线，随着周期的增加，预测值并未大幅偏离实测值，且在8～11周期预测效果最好，在一定程度上反映了间接DGM(1,1)不仅适合短中期预测，也适合长期预测，弥补了另两种模型不能进行长期预测的缺憾。

4 结 语

从3种模型对基坑沉降监测数据的预测效果来看，GM(1,1)与DGM(1,1)模型的预测值在7周期以后与实测值偏离越来越大，说明这两种模型仅适合短中期预测；间接DGM(1,1)的C值远小于另两种模型，因此预测精度要高于另两种模型；且其预测曲线与实测值曲线十分接近，说明它对短中期和长期预测均适用，弥补了另两种模型不能进行长期预测的缺憾。

[1] 杨华龙,刘金霞,郑斌.灰色预测GM(1,1)模型的改进及应用[J].数学的实践与认识,2011(23):39-46

[2] 李斌,朱健.非等间隔灰色GM(1,1)模型在沉降数据分析中的应用[J].测绘科学,2007(4):52-55

[3] 鲁纯.灰色建模中数据缺失值处理方法探讨[J].测绘通报,2013(7):12-15

[4] 李翠凤.灰色系统建模理论及应用[D].杭州:浙江工商大学,2006

[5] 崔先强,焦文海.灰色系统模型在卫星钟差预报中的应用[J].武汉大学学报(信息科学版),2005(5):447-450

[6] Camelia D. Grey Systems Theory in Economics: a Historical Applications Review[J]. Grey Systems,2015,5(2):263-276

[7] 谢乃明.灰色系统建模技术研究[D].南京:南京航空航天大学,2008

[8] 崔立志.灰色预测技术及其应用研究[D].南京:南京航空航天大学,2010

[9] 郭晓君,刘思峰,方志耕.基于标准区间灰数的发展带离散DDGM预测模型[J].数学的实践与认识,2014(6):19-25

[10] 聂爱秀,杨伟,刘英姿.改进的GM(1,1)模型及其应用分析[J].地理空间信息,2004,2(5):24-25

[11] 黄长军,曹元志,胡丽敏,等.基于新陈代谢GM(1,1)模型的益阳城市化水平分析[J].地理空间信息,2012,10(3):124-126

[12] 焦春义.DGM(2,1)优化模型研究应用[J].科技信息,2013(12):37-38

[13] 练郑伟,党耀国,王正新.反向累加生成的特性及GOM(1,1)模型的优化[J].系统工程理论与实践,2013(9):2 306-2 312

[14] 曾波,刘思峰.近似非齐次指数序列的DGM(1,1)直接建模法[J].系统工程理论与实践,2011(2):297-301