实时GLONASS相位频间偏差粒子群优化估计方法

隋 心，徐爱功，郝雨时，王长强

辽宁工程技术大学测绘与地理科学学院，辽宁 阜新 123000

2011年12月8日，俄罗斯GLONASS系统控制中心宣布GLONASS已具有全运行能力。迄今为止，除了GPS以外，仅有GLONASS具有全球定位和授时能力，因此很多研究团队对GLONASS的精密定位方法进行了研究[1-3]。由于GLONASS采用频分多址技术，因此不同卫星在GLONASS接收机端的未校准相位延迟(uncalibrated phase delays，UPD)也不同，这个差异称为接收机端相位观测值的频间偏差(inter-frequency bias，IFB)，本文将其简称为相位IFB。由于受到相位IFB的影响，不同卫星间双差模糊度将不再具备整数特性，不能固定为整数。因此相位IFB的特性以及GLONASS的双差模糊度快速固定始终是GNSS领域的研究热点之一。

已有研究成果表明，相同品牌的GLONASS接收机间具有近似的相位IFB值，但是对于不同品牌的GLONASS接收机，相位IFB可能会不同[4]。为避免由于接收机间的相位IFB不同而造成模糊度无法固定的问题，需要使用相同品牌的接收机进行基线数据采集[5]。但这个要求在实际野外数据采集过程中并不现实：由于GLONASS接收机生产厂家不断增加，使用不同品牌接收机共同作业的概率也在增加；此外，天线、天线连接线长度以及接收机的重启，也会对相位IFB产生影响[6]，这些情况均使得GLONASS模糊度固定变得更加复杂。

目前针对相位IFB特性的研究发现，相位IFB具有随频率线性变化的特征，相同类型接收机的相位IFB基本一致，两个频率(G1/G2)上相位IFB对应的几何距离偏差是一致的[3]。根据这些特征，提出多种GLONASS模糊度固定的方法。其主要思想是预先求出相位IFB参数，处理时作为改正数[7]。然而，由于模糊度参数与相位IFB的线性相关性，这些方法在估计相位IFB时，一般要求有相当长的观测数据和已知的测站坐标，在估计相位IFB时还要用同步的GPS观测数据来增加模糊度参数的稳定性，最终得到相应的相位IFB信息[8]。也正是因为这个原因，这些方法的效率很低，精度也有待提高。同时，这样的方法也很难满足实时定位中对相位IFB的快速野外标定的需要，因为相位IFB可能会受到环境的变化以及接收机重新启动的影响而发生变化。

为了实现相位IFB的快速估计，文献[9]采用粒子滤波对相位IFB进行估计，进而实现GLONASS模糊度快速固定。这种方法的优点为：①在没有增加待估参数数量情况下，采用搜索的方式实现GLONASS模糊度固定。②在没有相位IFB先验信息的情况下，采用较少历元的GLONASS数据便可实现模糊度固定。但该方法也存在一些不可忽视的缺点：已有研究结果表明，IFB变化率的取值范围非常小，通常只有给定的IFB变化率值距离真值在±4 mm/FN范围内才能使GLONASS模糊度固定。因此在使用粒子滤波进行参数估计过程中，粒子的采样间隔一般设置为1 mm/FN。由于最大的IFB变化率值小于0.10 m/FN，因此粒子的取值区间设为[-0.10,0.10] m/FN。根据粒子采样间隔以及取值区间，可以得出在粒子集合中粒子的总数为200个。这说明在进行参数估计过程中，每一历元需要进行200次的法方程构建、解算以及模糊度固定，而其中只有少数的几次解算才是有效的，这表明该算法的效率并不高，增加了计算负担，并且当GLONASS卫星个数较多或GLONASS与其他GNSS系统进行组合定位时，进行上述解算需要更多的时间，很难满足实时模糊度固定的要求，因此有必要采用更加高效的相位IFB估计方法进行研究，进而实现GLONASS的实时高精度动态定位。

粒子滤波方法的核心是利用一些随机样本来表示系统随机变量的后验概率密度，进而获得基于物理模型的近似最优数值解。为了能够更好地近似系统的后验概率密度，需要采用大量的样本，这是导致基于粒子滤波的相位IFB参数估计方法搜索效率不高的本质原因。粒子群优化算法(particle swarm optimization，PSO)不需要对搜索区间内的所有粒子进行遍历，可根据个体和群体历史最优位置来驱动粒子快速朝最优位置运动，效率较高，因此本文将采用该算法对相位IFB进行快速搜索，实现相位IFB的实时估计。

本文首先对GLONASS双差观测方程构建过程进行说明，然后将粒子群优化算法引入到相位IFB参数估计方法中，并对该算法的设计流程进行描述，利用试验对新方法的性能进行测试和分析，在最后一部分给出结论和展望。

1 GLONASS双差观测方程构建

顾及硬件延迟和初始相位偏差的GLONASS相位和伪距非差观测方程可表示为

(1)

在两台接收机a和b间求单差，卫星钟差被消除，卫星端的硬件延迟和初始相位偏差被消除，对于短基线，单差后的对流层延迟和电离层延迟可以被忽略。GLONASS站间单差相位和伪距观测方程可表示为

(2)

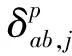
(3)

(4)

式中，αj为相位IFB常数项；Δγ为IFB变化率；kp为GLONASS卫星p的频率编号。

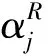
(5)

不同波长对双差模糊度固定的影响，目前主要存在3种处理方法。第一种方法为将以长度为单位的站间单差观测方程转换成以周为单位的站间单差观测方程[12]。第二种方法是以长度为单位建立观测方程，把两个不同波长的单差模糊度之差转换成为一个具有整数特性的双差模糊度以及一个与参考卫星单差模糊度有关的部分来解决由于波长不一致所带来的问题[13-15]。第三种方法是直接使用式(5)，将双差模糊度参数以单差模糊度参数的形式进行估计[16]，由于单差模糊度参数的个数多于双差观测值个数，这将导致法方程秩亏，为了解决该问题，通常给定单差模糊度参数初值，在估计得到单差模糊度浮点解之后，可以采用投影的方式将单差模糊度投影为以周为单位的双差模糊度[17]。从本质上来说，这3种方法是等价的，因为这3种方法均需要伪距观测值信息，只是使用该信息的方式不同而已[18]。然而，在选择参考卫星和组合不同系统观测值时采用第三种方法较方便[17,18]，因此本文采用第三种方法来消除不同波长对双差模糊度固定的影响。

2 基于粒子群优化算法的IFB变化率参数快速估计方法

将IFB变化率参数作为改正数，如果给定的IFB变化率值越准确，则在GNSS数据处理过程中得到的RATIO值就会越大，RATIO值可以对IFB变化率的准确性进行评价，因此可以根据RATIO值分布特点来设计IFB变化率参数快速估计方法。文献[9，18]对IFB变化率与RAITO值以及坐标偏差之间的关系进行了详细分析，因此本文不再详述，根据上述文献的试验结果可以认为：①在设定的搜索区域范围内，即使RAITO值出现多个峰值，但是只有最大的RATIO值对应着最优的IFB变化率参数，因此IFB变化率最优值的估计问题就转变为搜索RATIO值的最大峰值问题，而该问题可归结为求解最优化问题，求解最优化问题的优化方法可以快速有效的求解到全局最优解。②在一定范围内的IFB变化率取值均能够使GLONASS双差模糊度固定，即使取值不是IFB变化率的最优值，也可以得到高精度的定位结果，因此可以将非最优但可以满足一定约束条件的采样点作为最终的搜索结果，减少搜索次数，提高搜索效率，这对于高精度实时动态定位来说非常重要。

PSO算法是文献[10,19]提出的一种求解最优化问题的优化方法。根据IFB变化率与RATIO之间的关系分析，可以认为IFB变化率可采用搜索非最优但可以满足一定约束条件粒子的方式进行估计，而PSO正是采用一个约束条件来作为停止搜索的准则，因此，在这方面PSO也比较适合于IFB变化率的快速估计。为了能够满足高精度实时动态定位的要求，综合采用Kalman滤波和PSO算法对IFB变化率参数进行快速估计，具体流程可描述为：

(1) 如果为首历元，对状态向量X0(包括位置和模糊度参数，由于当前只考虑短基线情况，因此没有将对流层、电离层参数加入)及其方差协方差阵P0进行初始化，否则根据上一历元的状态向量信息对当前历元的状态向量信息进行一步预测，可表示为

(6)

(7)

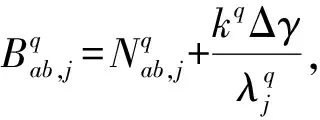
(3) 对式(7)进行线性化，误差方程可表示为

V=HX-Z,R

(8)

式中，V为误差项；H为系数阵，Z为OMC(observed minus computed)值，R为观测值的方差协方差阵。

(4) 采用Kalman滤波对状态向量进行解算

(9)

(5) 确定从单差模糊度到双差模糊度的投影矩阵D，将单差模糊度参数对应的方差协方差阵投影为双差模糊度对应的方差协方差阵，投影过程可表示为

DPDT=P′

(10)

式中，P与P′为投影前后的方差协方差阵。

(6) 将IFB变化率作为粒子群优化算法的搜索目标，对粒子群参数进行设置，包括粒子个数、群体最大迭代次数、最大和最小惯性因数、学习因子c1和c2、粒子位置变量的最大值和最小值、粒子速度变量的最大值和最小值以及迭代停止条件。

(7) 在指定的范围内，对粒子群进行随机初始化，包括随机位置和速度。

(8) 利用IFB变化率粒子对所有单差模糊度参数进行改正，改正公式可表示为

(11)

式中，xi为当前IFB变化率粒子的位置。

(9) 利用投影矩阵D，将改正后的单差模糊度参数投影为双差模糊度参数，投影过程可表示为

DX=X′

(12)

式中，X与X′为投影前后的状态向量。

(10) 在投影后的状态向量及方差协方差阵中提取出与双差模糊度有关的部分，采用LAMBDA方法进行双差模糊度固定[20]，将获取到的RATIO值作为当前粒子的适应度值。

(11) 根据粒子适应度值更新粒子个体的历史最优位置。

(12) 根据所有粒子个体的历史最优位置更新粒子群体的历史最优位置。

(13) 根据粒子个体的历史最优位置和粒子群体的历史最优位置更新粒子的位置和速度，更新过程见式(13)及式(14)

(13)

(14)

式(13)中

(15)

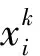
(14) 对更新后粒子的位置和速度进行限制：如果更新后的位置或速度超出指定的范围，则对该粒子的位置或速度重新进行初始化。

(15) 判断gbest所对应的适应度值是否大于给定阈值或者当前迭代次数是否大于群体最大迭代次数，如果已经满足以上迭代停止条件，将gbest作为IFB变化率的最优估值，否则，重复执行步骤(8)～(15)，直到满足迭代停止条件。

(16) 将确定出来的IFB变化率参数估值作为改正数对单差模糊度参数进行改正，使投影后的双差模糊度具有整数特性，采用LAMBDA方法进行双差模糊度固定，实现GLONASS双差模糊度实时固定，如果连续n(n≥5)个历元均为模糊度固定解，并且这n个历元所求得的n个IFB变化率参数估值十分接近，标准差小于某一阈值，则缩小下一历元粒子群的搜索范围，进一步提高粒子群搜索效率。

3 试验分析

选用一条8.6 km长的基线数据，该基线采用两种不同类型的接收机进行数据采集，两类接收机分别为TRIMBLE NETR9和JPS EGGDT，对应的天线分别为TRM57971.00和AOAD/M_T。基线数据采样间隔为30 s，观测时长为11 h 20 min。

为了能够将上述算法与基于粒子滤波的IFB变化率估计方法进行比较，利用本文所述方法首先采用单历元数据处理方式对基线双频观测数据进行处理。已有文献表明两个频率(G1/G2)上相位IFB对应的几何距离偏差是一致的[3]，因此本文将两个频率上的IFB变化率设定为一个参数。对粒子群参数进行设置：粒子个数设为10；群体最大迭代次数设为10；最大和最小惯性因数分别设为0.2和1.2；学习因子c1和c2均设为2；粒子位置变量的最大值和最小值分别设为-0.1和0.1；粒子速度变量的最大值和最小值分别为0.03和0；迭代停止条件中gbest所对应的适应度阈值设为4.5。试验统计结果见图1和图2。

如图1所示，在观测时段内，1360个历元中有98.6%的历元能够准确搜索出IFB变化率，只有极少历元无法准确确定出对应的IFB变化率估值，对于这些历元，其搜索次数已经达到最大搜索次数，并且对应的适应度也均小于3，说明无论采用何种方式进行搜索，均无法使这些历元的模糊度固定，出现这类现象的可能原因为这些历元的观测数据质量不佳，即使给定准确的IFB变化率改正值，采用单历元数据也无法进行模糊度固定，因而也无法准确搜索出IFB变化率。在本次试验中，采用本文所述方法进行IFB变化率搜索，每历元平均搜索次数为32次，而对于基于粒子滤波的IFB变化率估计方法，首先该方法很难实现单历元IFB变化率估计，通常需要一定数量的历元进行收敛；其次该方法的每历元平均搜索次数为200次。本次试验中单历元模糊度固定成功率达到96.2%(模糊度固定的标准设为RATIO≥3)，为了进一步验证模糊度固定的可靠性，将模糊度固定解和浮点解的定位精度进行对比分析。如图2所示，将模糊度固定解和浮点解的定位结果与其真值进行比较，红、绿、蓝色线条分别表示东(E)、北(N)、高(U) 3个方向上的模糊度固定解坐标偏差，灰色线条表示模糊度浮点解在3个方向上的坐标偏差。对图2所示坐标偏差数据进行统计，结果表明模糊度固定解坐标偏差在E、N、U 3个方向上的最大坐标偏差分别为11.7 mm、16.7 mm和36.7 mm，平均定位精度分别为0.3 mm、0.1 mm和0.5 mm，中误差分别为4.3 mm、4.8 mm和11.1 mm，而模糊度浮点解坐标偏差在3个方向上的最大坐标偏差分别为0.743 m、0.774 m和1.786 m，平均定位精度分别为0.062 m、0.012 m和0.127 m，中误差分别为0.183 m、0.205 m和0.484 m。以上的试验结果表明，使用本文所述方法可以高效准确地获得IFB变化率估值，同时也可以获得可靠的模糊度固定解。

单历元数据处理方式可以很好地检验算法的性能，但在实际实时动态数据处理过程中，通常采用滤波的方式对数据进行逐历元处理。利用本文所述方法对上述基线数据进行逐历元数据处理。粒子群参数设置同上。试验统计结果见图3和图4。

如图3所示，在观测时段内，所有历元都能够准确搜索出IFB变化率，其平均值为6.7 mm/FN，标准差为2 mm/FN；每历元平均搜索次数为9次；模糊度固定成功率为97.8%。相较于单历元数据处理方式，采用滤波方式的逐历元数据处理可以更好地发挥本文所述方法的优势。需要说明的是，相对于使用最小二乘和基于粒子滤波的IFB变化率估计方法，使用本文所述方法获取的IFB变化率并不够稳定，这是因为在使用粒子群优化算法进行IFB变化率最优值搜索过程中，需要同时顾及解算效率和精度，考虑到实时动态定位对解算效率的要求，实际需要的并不是绝对群体最优值，而是既能够满足模糊度固定所需基本条件又能够达到搜索次数最少效果的近似最优值，因此利用本文所述方法获取到的IFB变化率估值虽然不是十分稳定，但可以达到较好的模糊度固定效果。为了对本次试验中的模糊度固定解的定位精度进行分析，仅将满足模糊度固定标准的定位结果与其真值进行比较，如图4所示，在E、N、U 3个方向上的最大坐标偏差分别为11.7 mm、14.4 mm和31.4 mm，平均定位精度分别为0.1 mm、0.0 mm和0.1 mm，中误差分别为4.2 mm、4.6 mm和11.5 mm，以上统计结果说明利用本文所述方法获取的模糊度固定解十分可靠。

计算时间对于高精度实时动态定位来说非常重要，因此对上述试验所有历元的计算时间以及卫星个数进行统计，统计结果见图5。解算数据所使用的计算机的配置为：酷睿i5 CPU，2.5 GHz CPU主频，4 GB内存。图5表明，利用本文所述方法对IFB变化率参数进行估计，所有历元的计算时间均小于0.15 s，每历元平均计算时间为0.023 s。本试验同时对基于粒子滤波的IFB变化率估计方法所需时间进行统计，每历元平均计算时间为0.070 s。对这两种方法进行比较，本文所述方法相较于粒子滤波算法，解算效率提高了66%。图5也表明本文所述方法每历元所需时间并没有随着卫星个数的变化而发生明显变化，说明该方法的搜索次数与卫星个数不存在必然联系。

4 结 论

目前，世界上已经建成的全球导航卫星系统只有GPS和GLONASS，相较于GPS，GLONASS应用不够广泛，其主要原因是由于GLOANSS采用了频分多址技术，导致不同卫星在接收机端的UPD不同，产生了相位IFB，相位IFB与模糊度线性相关，很难在短时间内对相位IFB和模糊度进行分离，因此在当前的GNSS数据处理策略中，通常将GLONASS的双差模糊度不进行固定，只是将其作为GPS模糊度固定的一种辅助信息。为了解决该问题，文献[9]将粒子滤波引入相位IFB参数估计中，大幅提高了相位IFB参数与模糊度参数的分离速度，但当GLONASS卫星个数较多或GLONASS与其他GNSS系统进行组合定位时，粒子滤波方法需要更多的时间，很难满足实时模糊度固定的要求，需要进一步提高搜索效率。

图1 利用粒子群优化算法单历元估计IFB变化率及所需搜索次数的时间序列图Fig.1 Time sequence for IFB rate and number of searching by using PSO for single-epoch solution

图2 模糊度浮点解和利用粒子群优化算法单历元估计IFB变化率所对应的模糊度固定解定位精度统计Fig.2 Position differences with respect to the ground truth for single-epoch solution with integer ambiguity resolution and ambiguity float solution

图3 利用粒子群优化算法逐历元估计IFB变化率及所需搜索次数的时间序列图Fig.3 Time sequence for IFB rate and number of searching by using PSO for filtering solution

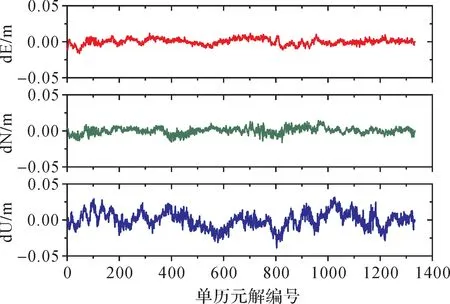
图4 利用粒子群优化算法逐历元估计IFB变化率所对应的模糊度固定解定位精度统计Fig.4 Position differences with respect to the ground truth for filtering solution with integer ambiguity resolution

图5 不同IFB变化率估计方法所需时间统计Fig.5 The computational time for different estimate methods for IFB rate

本文在已有的相位IFB特性研究成果的基础上，推导了顾及IFB影响的GLONASS双差观测方程，在此基础上，通过对相位IFB与RATIO值之间的关系分析，认为可将相位IFB估计问题归结为求解最优化问题，提出采用优化方法中的粒子群优化算法进行相位IFB参数快速估计，并对该算法的流程进行了详细设计，最后利用试验对提出方法的性能进行测试和分析。试验结果表明，在单历元解算条件下，利用本文所述方法对IFB变化率最优值进行搜索，每历元平均搜索次数为32次，远低于粒子滤波算法的200次；在采用Kalman滤波方法进行解算条件下，每历元平均搜索次数仅为9次。无论采用单历元解还是采用滤波解，模糊度固定成功率均高于96.2%，模糊度固定解的最大坐标偏差均小于4 cm。因此可以说明利用本文所提出的基于粒子群优化算法的相位IFB参数快速估计方法能够满足GLONASS高精度实时动态定位要求。

参考文献：

[1] PRATT M, BURKE B, MISRA P. Single-Epoch Integer Ambiguity Resolution with GPS-GLONASS L1-L2 Data[C]∥Proceedings of the 11th International Technical Meeting of the Satellite Division of the Institute of Navigation. Nashville, TN: Institute of Navigation, 1998, 11: 389-398.

[2] WANG Jinling, RIZOS C, STEWART M P, et al. GPS and GLONASS Integration: Modeling and Ambiguity Resolution Issues[J]. GPS Solutions, 2001, 5(1): 55-64.

[3] WANNINGER L, WALLSTAB-FREITAG S. Combined Processing of GPS, GLONASS, and SBAS Code Phase and Carrier Phase Measurements[C]∥Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation. Fort Worth, TX: Fort Worth Convention Center, 2007: 866-875.

[4] WANNINGER L. Carrier-phase Inter-frequency Biases of GLONASS Receivers[J]. Journal of Geodesy, 2012, 86(2): 139-148.

[5] TAKZC F. GLONASS Inter-frequency Biases and Ambiguity Resolution[J]. Inside GNSS, 2009, 4(2): 24-28.

[6] CHEN Junping, XIAO Pei, ZHANG Yize, et al. GPS/GLONASS System Bias Estimation and Application in GPS/GLONASS Combined Positioning[C]∥SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin, Heidelberg: Springer, 2013: 323-333.

[7] ZINOVIEV A E, VEITSEL A V, DOLGIN D A. Renovated GLONASS: Improved Performances of GNSS Receivers[C]∥Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009). Savannah, GA: Savannah International Convention Center, 2001: 3271-3277.

[8] AL-SHAERY A, ZHANG S, RIZOS C. An Enhanced Calibration Method of GLONASS Inter-channel Bias for GNSS RTK[J]. GPS Solutions, 2013, 17(2): 165-173.

[9] TIAN Yumiao, GE Maorong, NEITZEL F. Particle Filter-based Estimation of Inter-frequency Phase Bias for Real-time GLONASS Integer Ambiguity Resolution[J]. Journal of Geodesy, 2015, 89(11): 1145-1158.

[10] KENNEDY J. Particle Swarm Optimization[M]∥SAMMUT C, WEBB G I. Encyclopedia of Machine Learning. Boston, MA: Springer, 2011: 760-766.

[11] POVALIAEV A A. Using Single Differences for Relative Positioning in GLONASS[C]∥Proceedings of the 10th International Technical Meeting of the Satellite Division of the Institute of Navigation. Kansas City, MO: Institute of Navigation, 1997, 97: 929-934.

[12] LEICK A, LI J, BESER J, et al. Processing GLONASS Carrier Phase Observations-Theory and First Experience[C]∥Proceedings of the 8th International Technical Meeting of the Satellite Division of the Institute of Navigation. Palm Springs, CA: Institute of Navigation, 1995: 1041-1047.

[13] WANG J. An Approach to GLONASS Ambiguity Resolution[J]. Journal of Geodesy, 2000, 74(5): 421-430.

[14] 姚宜斌, 胡明贤, 许超钤. 基于DREAMNET的GPS/BDS/GLONASS多系统网络RTK定位性能分析[J]. 测绘学报, 2016, 45(9): 1009-1018. DOI: 10.11947/j.AGCS.2016.20160133.

YAO Yibin, HU Mingxian, XU Chaoqian. Positioning Accuracy Analysis of GPS/BDS/GLONASS Network RTK Based on DREAMNET[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1009-1018. DOI: 10.11947/j.AGCS.2016.20160133.

[15] 段举举, 沈云中. GPS/GLONASS组合静态相位相对定位算法[J]. 测绘学报, 2012, 41(3): 825-830, 917.

DUAN Juju, SHEN Yunzhong. An Algorithm of Combined GPS/GLONASS Static Relative Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 825-830, 917.

[16] TAKASU T, YASUDA A. Development of the Low-cost RTK-GPS Receiver with an Open Source Program Package RTKLIB[C]∥International Symposium on GPS/GNSS. Jeju: International Convention Center Jeju, Korea, 2009: 4-6.

[17] KOZLOV D, TKACHENKO M. Instant RTK cm with Low Cost GPS+GLONASS C/A Receivers[C]∥Proceedings of the 10th International Technical Meeting of the Satellite Division of The Institute of Navigation. Kansas City, MO: Institute of Navigation, 1997, 10: 1559-1570.

[18] TIAN Yumiao. Online Estimation of Inter-Frequency/System Phase Biases in Precise Positioning[D]. Berlin: Technische Universität Berlin, 2016.

[19] EBERHART R, KENNEDY J. A New Optimizer Using Particle Swarm Theory[C]∥Proceedings of the 6th International Symposium on Micro Machine and Human Science. Nagoya, Japan: IEEE, 1995: 39-43.

[20] TEUNISSEN P J G. The Least-squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82.