聚焦“有序” 促进儿童数学思维生长

比利时科学家普里戈金在《从混沌到有序：人与自然的新对话》一书中强调：一切事物都按照相对有序的状态在发展。我国明代学者尤为“尊序”和“遵序”，其中明哲学对“有序”阐述较多。现代数学教育理论认为：数学知识本身是非常重要的，但是对学生后续的学习、生活和工作长期起作用并使其终身受益的是数学思维。促进儿童思维生长旨在引导他们自主激活知识，积累学习经验，保证其数学学习高效进行。笔者致力于“有序”的数学教学，注重呵护儿童的数学思维生长，以期帮助他们实现学习能力最大化、最持久化。

一、“无序”教学的现象分析和“有序”的内涵特征

在小学数学教学中，由于教师片面注重教学结果而又欠缺思维秩序的维护，使得许多学生知识记忆僵硬、学习方法繁杂、数学思想混乱。

（一）“无序”教学的现象分析

1.满足于就题论题，滞留于记忆复制层面，缺乏举一反三的精神。

在解决数学问题的过程中，无论是教师还是学生往往专注于就题论题，而忽略知识的迁移联结，从而导致原问题稍微“改头换面”就成为学生新的拦路虎，教师和学生则疲于不断解决相似的问题。如苏教版二下“由4、6、1三张卡片可以组成多少个不同的三位数？”这个问题，班级大多数学生都能找到6个不同的三位数，教师满意于学生的掌握情况，往往一带而过，可是增加一个数字变成4张卡片组成四位数时，学生遗漏、重复的错误就如雨后春笋般冒出，究其原因，盖因学生在学习三个数字组合的过程中思维是杂乱无章、无规律可循的。

2.热衷于“散沙式教学”，徘徊于浅表学习层面，缺乏综观全局的眼光。

“散沙式教学”是一种浅尝辄止且支零破碎的教学方式，教师专注于教学方式而忽视儿童立场，无法帮助学生形成知识之间的意义联系，从而导致学生经验断裂，数学学习如“蜻蜓点水”。比如，在低年级的整数运算、中年级的小数运算、高年级的分数运算教学中，教师缺乏综观全局的眼光，只关注计算结果，而忽视它们本质相同的算理——相同计数单位的数相加减，导致学生在异分母分数加减法运算中生搬硬套、屡错不改。

3.紧盯着结果正误，执着于教师主导层面，缺乏延续发展的思维。

当下，许多教师在课堂上仍以“得出结论，结果准确”为原则，把学生不断尝试和探索过程中出现的错误直接忽略，导致其主动性和创造性难以得到发挥，学习激情和潜力难以被唤醒。如教学苏教版一下《认识人民币》，一张五角纸币能换（ ）张一角纸币和（ ）张二角纸币。一年级学生初次在真正意义上认识人民币，第一次实践操作时完全是无序的，凭着感觉拿出五角纸币，汇报也大多随意而凌乱，许多教师认为这是“无用功”，往往直接示范，殊不知学生思维生长的契机就这样白白流失了。

（二）“有序”的内涵诠释

序，是事物的结构形式，指事物或系统组成诸要素之间的相互联系。有序，是指物质的系统结构或运动是确定的、有规则的。思维有序，是指思考和解决问题时遵循一定的规则、秩序，按照特定的线索和步骤去探索的思维方式。思维有序具有注重将事物、问题条理化、层次化，让思路清晰、行动有序的特征。苏教版教材中的有序思想作为“策略性知识”贯穿整个小学数学学习阶段。

二、“有序”促儿童数学思维生长的价值意蕴

促进儿童的思维由“无序”循序渐进为“有序”，既顺应儿童的思维发展特点，又能为其今后的思维生长奠定良好的基础。

（一）知识技能意蕴

“有序”致力于引领儿童的知识学习从散点状走向结构化，以激发其整体思维的萌芽。法国数学家嘉当说：“数学规律的存在就如密密麻麻的‘蜂眼’，最后却以一整个‘蜂巢’示人。”数学知识学习所呈现的不应是毫无关联的散状，而应是完整清晰的结构。“有序”要求教师从确定教学目标、选择教学内容、运用教学手段等方面进行整体上的建构，给儿童一个循序渐进、整体全面的学习体验。儿童的思维既“懵懵懂懂”又极具敏感性。在数学教学中，教师如果能充分利用多元表征，让儿童学会有序地看、说和操作，从而能有序地思，那么儿童将于“序”中既增知识又长智慧。

（二）核心素养意蕴

“有序”致力于引发儿童的数学逻辑从模糊走向清晰，以夯实其逻辑思维的基础。叶澜教授曾说：“课堂应是向未知方向挺进的旅程，而不是一切都必须遵循儿童思维发展特点而没有激情的行程。”有序的数学课堂旨在帮助儿童建立数学逻辑，把他们脑中支离破碎的数学思想进行整理、排序、优化，逐渐规范为数学经验与逻辑能力。核心素养以学生为母体，在长期的数学学习过程中孕育成长，这种自我修养的积淀具有综合性、整体性和持久性，是奠定儿童今后数学学习的基石。

（三）发展成长意蕴

“有序”致力于引导学生的数学思考从割裂走向连贯，以促进其联结思维的生长。儿童思维能力的表达与运用是基于自主思考自主构建的，也许有的儿童思维层次较低或者停滞不前，但是只要他能有意识地去建构自己的思维，积极主动地展现自己的思考能力，就具有深刻的教育意义。

教师应真正把儿童放在课堂中央，放手让他们观察、猜想、推理和交流，以有序的教学理念与课堂实践塑造儿童的思维雏形。

三、“有序”促儿童数学思维生长的教学策略

（一）教师的“有序”教学让儿童的数学思维生长真正发生

在小学数学教学中，教师应充分明晰儿童的思维发展特点，遵循儿童的思维发展规律，适时进行调控，为他们的思维生长指明方向、保驾护航。

1.知识有序——遵循前后知识的逻辑递进。

特级教师吴正宪曾经说过：知识的传授应立足儿童的思维发展水平，它是循序渐进的，不可一蹴而就。有序思维促进知识学习的方式类似于“DNA模式”，使儿童在螺旋上升的过程中逐渐建构起知识结构，完善知识体系。

2.方法有序——实现学习方法的严谨串接。

思维有序能在儿童学习新知时有效地促进其思考、提炼与总结学习方法，这些经验又能在儿童遇到新的数学问题时起到正向的迁移作用。

3.活动有序——达成活动经验的清晰观照。

数学活动是儿童学习数学的“游乐场”，而在活动中有效提取经验需要借助有序的思维，帮助儿童厘清活动目标、活动重点以及活动预期。教学苏教版五上“多边形的面积”这一单元，笔者引导学生以熟悉的长方形为起点逐步向平行四边形、三角形、梯形演化，多边形面积计算公式的推导在图形演化的过程中随之有序生成。

4.思想有序——催生数学思想的无痕渗透。

苏霍姆林斯基说：每一个儿童都可能成为探索者、发现者、研究者。数学思想凝练于数学知识，它隐形贯穿于小学生数学学习的各个阶段，并为其知识的生长延续提供巨大的力量。思维有序可以促进儿童数学思想的条理化、规范化，让儿童的“思维之苗”从萌芽阶段就呈现出端正、有序、蓬勃的发展态势。教师的“点睛之笔”其实是引导儿童透过现象看本质，儿童紧紧围绕数量关系式进行“变与不变”的数学推理，思维更趋向有序。

（二）儿童的“有序”觉醒为其自身的数学思维生长“推波助澜”

思维的发展由低向高层层推进，并由于思维层次的不断积累而有意识地组合、叠加，最终在解决问题的过程中厚积薄发。

1.在历练与成长中循序获取知识，提高思维抽象度。

教师有序、睿智的教学策略可助力儿童借助表象逐步抽象，为有效培养和提升其数学思维的有序性提供肥沃的“土壤”。

以一年级的认识图形教学为例，在上学期《认识图形（一）》的课堂上，笔者和学生的交流是这样的：“正方体、长方体的积木看得见、摸得着”“他们都四四方方，有棱有角，能站得稳，不能滚”。这一课的练习对学生的要求也仅限于从一堆物体中找出所指定的，下学期的课本情境同样以积木为载体，却要求学生抽象出正方形、长方形来，这就需要他们更深入、更抽象地认识正方体、长方体。教师引入“像正方体和长方体这样的叫作立体图形”的认识，经过实践操作、讨论交流，学生知道正方体和长方体都有6个面，正方体的6个面都是相等的正方形，而用长方体可以画出长方形的面来，并深刻感知正方体、长方体这样的立体图形与正方形、长方形这样的平面图形的区别。在这个过程中，教师逐步引领学生学会用抽象的眼光看实物和有序地表达。

2.在积累与运用中逐步增强能力，实现思维多元化。

新课标指出：学生学习应当是一个生动活泼的、主动的和富有个性的过程。在数学教学中，教师应适时洞察“意外通道”，捕捉“美丽图景”，睿智机敏地进行引导。思维多元化教学为引导学生形成良好的思维方式铺设了一条坚实之路，于有序中培养其良好的思维习惯。苏教版四下的一次练习课，笔者和学生共同讨论一道思考题：“小明和小军拿出同样的钱合买练习本，买了以后，小明比小军多拿了10本，因此小明需给小军5元钱，一本练习本多少钱？”大部分学生在初步感知的基础上能深入思考，并画出线段图（如图1）。正确的解答是“10元对应 10本练习本，所以 10÷10=1（元）”。笔者偶然发现有个学生另辟蹊径，给出了不一样的解答：如果小明给小军5本两人就同样多，而这5元就对应5本，所以5÷5=1（元）。

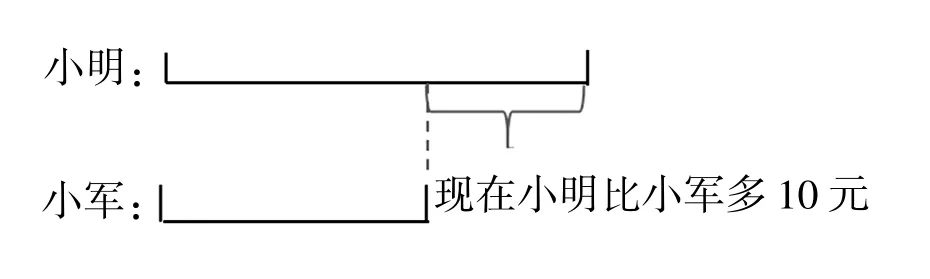
（图1）

笔者对该生另辟蹊径的思考角度和探索方法及时给予鼓励，全班学生都得到了思维的碰撞和洗礼。每个学生的思维潜力都无可估量，只要巧妙自然地催化，相信他们思维的幼芽一定能在潜移默化中茁壮生长。

3.在拓展与感悟中稳步提升素养，促进思维自觉化。

变封闭、被动、个体、静态的思维为开放、主动、集体、动态的思维，是基于儿童的生命存在、生命成长和生命发展来考量的。自觉思维是通过观察、猜测、假想做出实验性结论或直接了解和认识事物的一种思维形式。在数学学习过程中，培养学生的数学自觉思维能力，对激发他们的学习兴趣，使他们掌握探究方法、提升数学素养具有重要的意义。

悟性作为素养的直接体现，是学生深度学习过程中不断积累的隐性能力。笔者欣喜于课堂上学生悟性的萌芽，倾心于为它的破土而出和茁壮成长助力。在执教苏教版五下《圆的面积》一课时，笔者先展示一组图（如图2）。大部分学生都能概括出图的意思：“把圆等分成一些小扇形，拼在一起就是近似的平行四边形。”这时，教师抛砖引玉：“既然是近似的平行四边形，那如何求面积？”一番激烈争论后，一部分学生大胆地猜测：“无限分下去，最后分得很小很小的等腰三角形拼在一起就是平行四边形，而且当三角形足够小时，它的腰就是平行四边形的高。”极限的雏形已在学生脑中萌芽，或许他们自己未意识到，但这种思维能力已生根发芽，其思考问题的深度实现了质的飞跃。

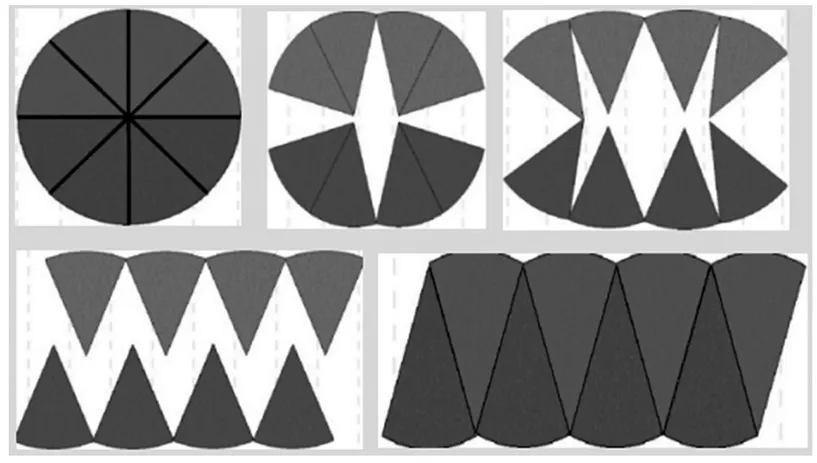
（图2）

总之，从本质上看，儿童思维的培养是一种基于学习的自然生长过程。生长需要土壤、水分、阳光，而“有序”的渗透，以其独特的价值，将成为儿童多重思维能力和数学核心素养提升的助推器。