基于ABAQUS的某制导子弹挤进压力有限元分析

刘 怡，王惠源，边朝阳

(中北大学 机电工程学院， 太原 030051)

制导子弹与传统子弹相比具有射击精度高、抗干扰能力强和效费比高的特点，这使得制导子弹成为弹药领域又一个新的发展热点。美国桑迪亚实验室在2012年2月份展示了一颗10 cm的制导子弹(见图1)，其在头部光学传感器的指引下，通过可动尾翼产生的气动力，可以在飞行中改变飞行方向从而精确击中1.6 km外的目标[1]。该型制导子弹不同于普通枪弹，它并不靠膛线来旋转并直线飞行，发射制导子弹的枪管内没有膛线，所以是一种滑膛枪。国内也开展了制导子弹技术的研究工作，发射原理和国外相同，均是采用滑膛枪管发射。在内弹道计算中，挤进压力是按已知量给出的，挤进压力的大小与弹带材料、结构、尺寸及其公差有关，有一定的随机散布[2]。本研究采用有限元分析与试验相结合的方式研究制导子弹的挤进压力。

1 挤进过程描述

在内弹道时期，弹丸在启动压力的作用下开始运动，由于普通子弹的弹丸直径略大于膛线内阳线的直径，在挤进过程中弹体圆柱部逐渐嵌入膛线，弹丸表面留有明显刻痕。制导子弹在挤进过程中，由于枪管内没有膛线，且弹带尺寸和身管内径属于过盈配合，弹带在挤进身管时产生整体的塑性变形，而弹丸表面没有刻痕。制导子弹的弹带挤进过程如图2所示，当弹带前端面A与坡膛接触时挤进过程开始，到后端面B运动到前端面初始位置时挤进过程结束。

孙河洋等[3]研究了坡膛结构变化对弹带挤进过程的影响，揭示了坡膛裂纹的形成机理。樊黎霞、何湘明[4]对弹丸挤进过程进行了有限元模拟，分析了挤进前后弹头壳和铅芯的变形特征及挤进结束后弹丸的残余应力。李强、吴宝双等[5]以某速射武器弹丸挤进过程为研究对象，研究了身管阳线在弹壳表面压痕的形成过程等非线性接触问题。上述研究均未涉及以制导子弹为代表的滑膛枪弹挤进压力的分析，而挤进压力对于内弹道的计算至关重要。

以某制导子弹挤进过程为研究对象，基于 ABAQUS软件对该过程做有限元分析，将模拟的结果与模型试验数据进行对比分析并得出结论，为制导子弹的结构设计与内弹道计算提供理论依据。

2 材料模型分析与理论依据

材料模型用来描述材料的力学性质，表征材料变形过程中的动态响应。在材料微观组织结构一定的情况下，流动应力受到变形程度、变形速度及变形温度等因素的影响非常显著。这些因素的任何变化都会引起流动应力较大的变动。因此材料本构模型一般表示为流动应力与应变、应变率、温度等变形参数之间的数学函数关系。

该模型中，身管材料采用普通炮钢，材料为35CrNiMoVA，弹丸壳体采用合金钢，在弹头圆柱部覆盖一层约0.5 mm厚的黄铜作为弹带，满足闭气的同时减少枪管磨损，材料性能参数如表1所示。

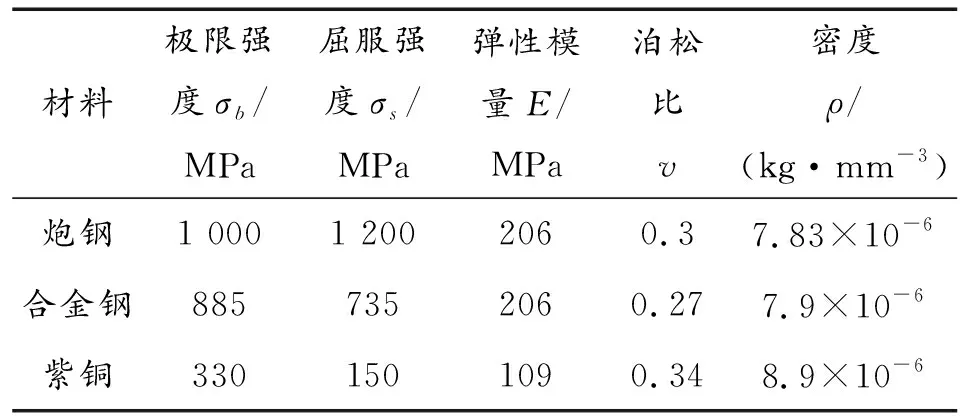
表1 材料属性参数

当前常用的塑性材料本构模型主要有：Bodner-Paton、Follansbee-Kocks、Johnson-Cook、 Zerrilli-Armstrong等模型。弹带在挤进过程中会产生塑性变形，且与枪管内壁摩擦产生高温，在上述模型中只有Johnson-Cook模型描述材料高应变速率下热黏塑性变形行为。Johnson-Cook模型认为材料在高应变速率下表现为应变硬化、应变速率硬化和热软化效应，Johnson-Cook模型为

式中：A，B，n为表征材料应变强化项系数；c为表征材料应变速率强化项系数；m为表征材料热软化系数；一般取小数；以上5个参数为材料性能常数，由材料拉伸试验得到，如表2所示。其他参数为：σ为Von-Mises等效应力；εp为等效塑性应变；ε为应变率；ε0为参考应变率，一般取1/s；T为试验温度；Tm为材料融点；TΓ为材料的相对参考温度。

3 建立有限元模型

由制导子弹和枪管的几何形状可知，两者均为轴对称模型。按照轴对称、平面应力或平面应变问题建模可以将三维问题简化为二维问题，大大降低模型的规模，缩短计算时间。制导子弹的弹带部位与枪管过盈配合，在挤进过程中弹带会发生塑性变形，同时与枪管内壁产生摩擦，塑性阻力的轴向分量与摩擦阻力构成了弹丸的挤进阻力。由于这一过程时间极短，可认为弹丸匀速挤进，则挤进压力与挤进阻力大小相等方向相反。

3.1 建立模型

使用 ABAQUS自身的建模工具，建立轴对称有限元模型。选用4种弹带形状：矩形弹带、弧形弹带、梯形弹带和三角形弹带(如图3所示)。

由于弹带材料相对于弹体和身管较软，故将弹带设置为可变形部件，将弹体设置为离散刚体，将身管设置为解析刚体[6]。在为弹带定义材料时，选择Johnson-Cook塑性模型，并按表2输入各参数。

表2 J-C模型中紫铜的材料常数

3.2 网格划分与边界约束条件

弹体属性为离散刚体，故设置为RAX2二结点线性轴对称刚性单元；身管为解析刚体，不需要划分网格。将弹带截面分割为两个部分，种子尺寸分别为0.025和0.005，两个部分的网格属性均为结构—最小化网格过渡，单元类型选择CAX4R四结点双线性轴对称四边形单元，减缩积分，沙漏控制。划分网格结果如图4所示。

因为弹带是压入弹体的弹带槽中，所以在弹体与弹带中添加绑定约束；弹带在挤进过程中与身管摩擦，定义弹带与身管的接触类型为罚函数，摩擦因数设置为0.19。在模拟过程中将身管完全固定。

在分析中采用ABAQUS/Standard模块，时间总长度设置为0.1 ms，对弹体的参考点添加0.5 mm的边界位移。

4 结果分析

弹带挤进身管的过程是复杂的非线性问题，时间非常短，采用ABAQUS软件能很好地模拟弹带挤进过程中的弹带变形和应力变化。弹带完全挤进后的应力云图如图5所示。

本研究假设弹丸匀速挤进身管，弹体参考点在轴向的反作用力RF2即为弹丸挤进压力，从场输出中建立XY数据，并绘制曲线，如图6所示。

取弹带中点为参考点，研究弹带在径向的塑料变形，从场输出中建立XY数据，并绘制曲线，如图7所示，弹带的径向变形量为0.005 mm。

在图6中，由于身管坡膛存在圆角过渡，弹带外轮廓不同，因此在软件分析中弹带与身管建立接触的时间不尽相同。由于在建模过程中，弹体外径与身管内径的尺寸相同，故在建立接触之前，作用力为0，4种弹带与身管接触过程中的起始时间与挤进压力(峰值与稳定值)如表1所示。

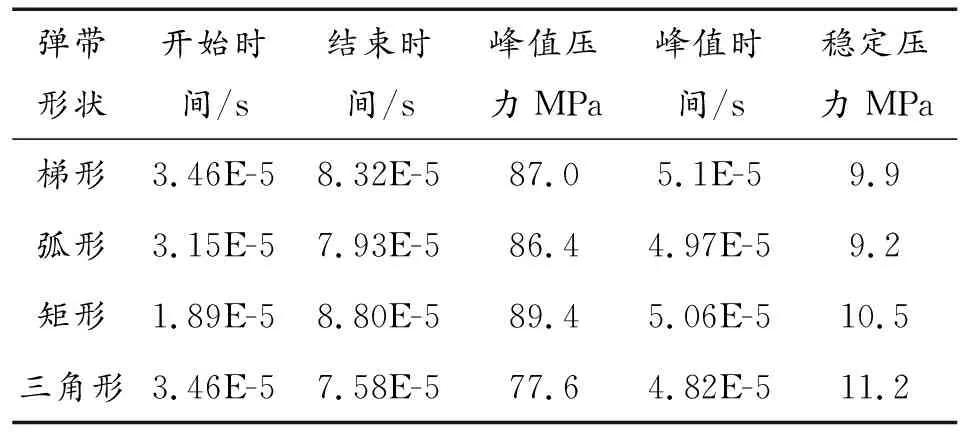
弹带形状开始时间/s结束时间/s峰值压力MPa峰值时间/s稳定压力MPa梯形3.46E-58.32E-587.05.1E-59.9弧形3.15E-57.93E-586.44.97E-59.2矩形1.89E-58.80E-589.45.06E-510.5三角形3.46E-57.58E-577.64.82E-511.2

本文采用的弹带过盈量为0.005 mm，研究4种弹带形状对挤进压力的影响。从表1可以看出，4种弹带中，结束时间、峰值时间与稳定压力基本接近，而开始时间和峰值压力变化较大，因此在试验中重点放在测量峰值压力与稳定压力上。

5 模型试验

在模型试验中，为尽可能准确地模拟弹带挤入过程，采用动态静力测压力方法，试验原理如图8所示

将主动件、压力传感器和弹丸连接到一起，通过外部机构给予主动件5 m/s的恒定速度模拟弹带挤入。试验中每种弹带进行3次试验，记录峰值压力与稳定压力的平均值，如表2所示。

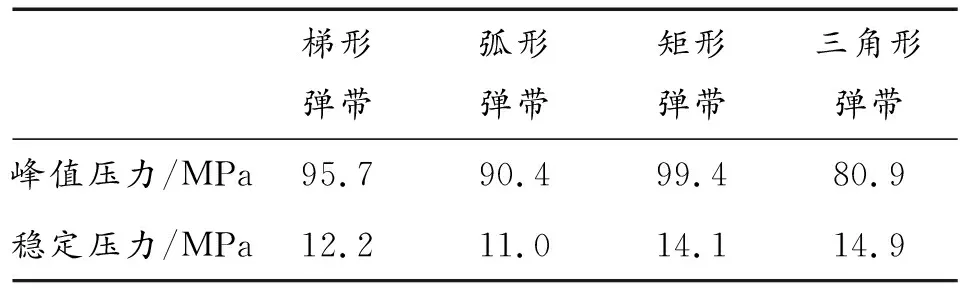
表2 3次试验所得峰值压力与稳定压力平均值

从表2可以看出，峰值压力与稳定压力的分布与分析结果基本一致，但有一个明显不同，即试验数据均高于软件分析结果。

弹带挤入身管的过程是内弹道全过程的一个初始阶段，但该阶段的现象非常复杂。弹带的快速变化涉及材料塑性力学问题，且该阶段的行程与时间非常短，难以用试验准确测量。对于该试验的误差，主要考虑以下几个因素：① 软件分析中属于理想化的数值计算，与材料真实的动态响应存在出入；② 弹带挤入过程并非匀速；③ 材料受温度的影响，力学性能存在波动。

6 结论

制导子弹作为新兴的精确制导武器以其优异的作战效能而广受关注。因其飞行过程中不需要依靠旋转稳定，大大简化了枪管的加工难度，也提高了枪管的寿命。但制导子弹的发射依然是经典内弹道的范畴，也需要弹带密闭燃气，本文采用有限元分析软件，对4种弹带的挤进阻力进行了分析，同时设计了模型试验。由于本文仅采用一种材料，所得数据有限，仅为制导子弹的弹带设计与试验提供一定的参考。

[1] 魏泽宇,冯秀莲,刘山,等.制导子弹的发展现状与关键技术[J].飞航导弹,2015(10):38-42.

[2] 金志明.枪炮内弹道学[M].北京:北京理工大学出版社，2004.

[3] 孙河洋，马吉胜，刘伟,等.坡膛结构变化对弹带挤进过程影响的研究[J].振动与冲击，2011(11):30-33.

[4] 樊黎霞，何湘明.弹丸挤进过程的有限元模拟与分析[J].兵工学报，2011(6):963-969.

[5] 李强，吴宝双，申玉波，等.基于ABAQUS弹丸挤进坡膛过程的有限元分析[J].机械设计，2015,32(4)：61-65.

[6] 石亦平，周玉荣.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2006.