基于误差分离技术的圆度误差评定测量软件设计

李 战，刘玉梅，张 华

(沈阳理工大学 机械工程学院，辽宁 沈阳 110159)

0 引言

误差分离技术是测试技术中的一种信息处理方法，即从所测得的误差信号中将所需要的误差提取出来，是现代计算机科学和信息技术渗透传统的机械制造领域,经多学科交叉与综合所形成的充满活力且富有前途的新兴学科分支。国防科技大学精密工程研究室在航天部及国家自然科学基金支持下，针对超精密加工圆度的多传感器在位检测、误差分离和补偿加工方法进行了全面研究[1-3]。三点法圆度误差测量与误差分离技术是最基本的方法，但将这一技术成功应用于加工的在位或在线测量中还不多见[4]。要将这一技术成功应用于在位或在线测量，必须在测量信息采集的硬件实现方面及测量信息处理分析显示的软件方面进行不断研究。

1 基于误差分离技术的圆度误差评定测量软件设计总体方案

首先，测量软件要有精确的数据计算与分析功能，利用基于误差分离技术的圆度测量方法，采用三点法(即用三个传感器按一定位置分布在被测对象周围)同时采集数据，数据处理后分离得到的被测零件的形状误差是原始的测量数据，再用最小二乘法建立数学模型评定圆度误差；其次，测量软件要有联机调试、参数输入、数据采集、图形显示、误差评定、数据存储调用的功能。基于误差分离技术圆度误差评定测量软件的设计分两大部分，人机交互界面设计与计算软件设计。

2 人机交互界面设计

为了完成计算软件的输入、输出、评定、图形显示及程序验证，需要建立人机交互界面，人机交互界面的设计框图如图1所示。人机交互界面中包括自动数据采集、图形显示、参数评定、手动数据输入、坐标轴范围设置、数组显示、最小二乘法参数显示以及系统参数输入等。

依据设计框图应用MATLAB设计的人机交互界面如图2所示，其作用为：①自动采集传感器测量的数据；②在下方作图处显示出图形；③用最小二乘法和误差分离计算出一系列数值；④当有已经测量好的数据时，手动输入数据；⑤打开图形比较软件，进行图形比较分析验证软件的正确性；⑥绘图时人工设置坐标范围，可以使图形更清晰；⑦用于显示误差分离处理之后的数组；⑧用于显示最小二乘法圆心、圆度误差以及半径偏移量e；⑨系统参数输入，包含α、β、N、r和放大倍数。

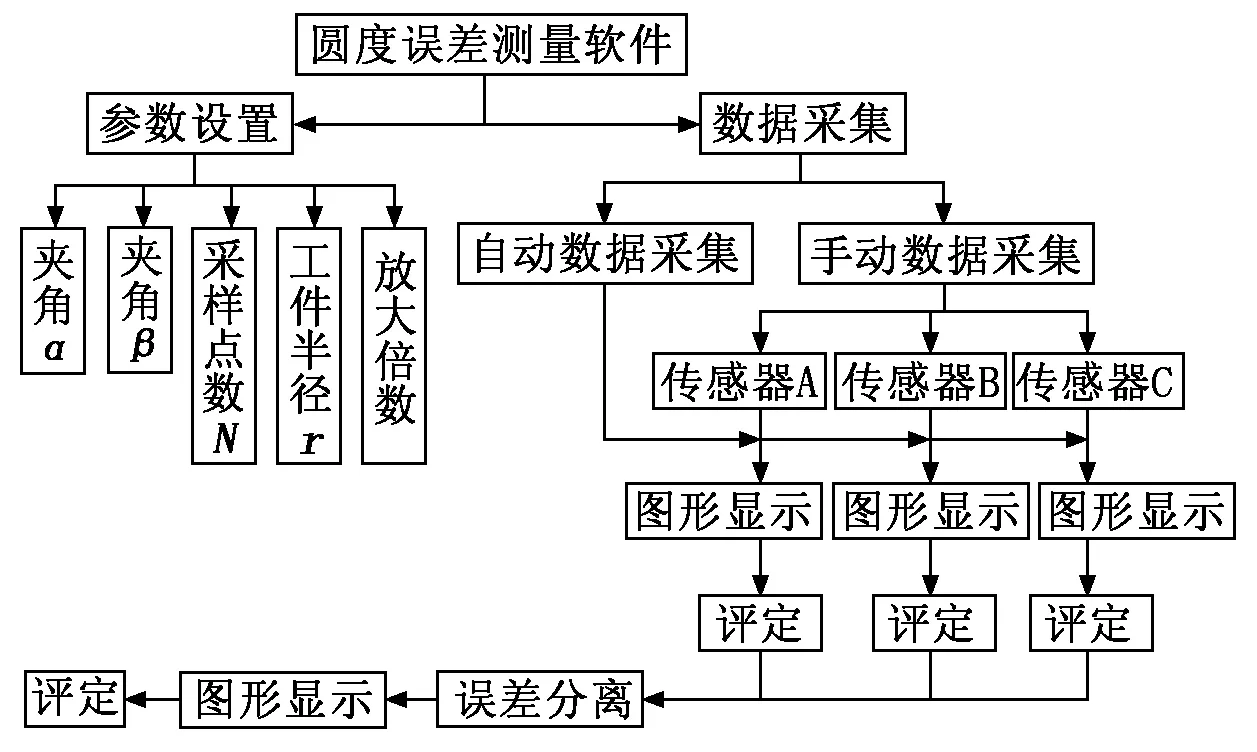
图1 人机交互界面设计框图

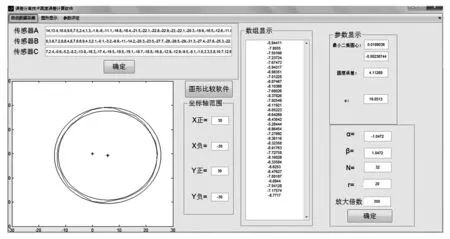
图2 人机交互界面(A传感器)

3 基于误差分离技术圆度误差评定计算软件设计

基于误差分离技术的圆度测量可分为反向法、多点法和多步法。多点法又分两点法、三点法、四点法及混合法，其中三点法圆度误差测量与误差分离技术是最基本的方法，其他方法可以看成这一基本方法的特例[5]，本文采用三点法测量的误差分离技术，将分离掉系统误差的数据用最小二乘法评定出圆度误差，以此建立数学模型编写出计算评定程序。

3.1 三点法圆度测量与误差分离技术的原理与数学模型

为了完全分离回转误差和圆度误差，可将3个传感器呈一定的夹角放置，如图3所示。3个传感器分别位于A、B、C点，其轴线交于O点。作固定的直角坐标系OXY，传感器A的轴线与Y轴重合，α和β分别为传感器B和C的轴线与Y轴的夹角，O1为被测工件回转中心，e(θ)、δ(θ)分别为轴系回转误差中的偏心距及偏心角。若工件的圆度误差为s(θ)，当工件旋转时，3个传感器的输出信号PA(θ)、PB(θ)、PC(θ)分别为：

PA(θ)=s(θ)+e(θ)cosδ(θ).

(1)

PB(θ)=s(θ-α)+e(θ)cos[δ(θ)+α].

(2)

PC(θ)=s(θ+β)+e(θ)cos[δ(θ)-β].

(3)

将上述3个信号组合成信号PD(θ)：

PD(θ)=PA(θ) +bPB(θ) +cPC(θ).

(4)

其中：b、c为加权系数。将式(1)～式(3)代入式(4)，整理得：

PD(θ)=s(θ)+bs(θ-α)+cs(θ+β)+e(θ)cosδ(θ)[1+bcosα+ccosβ]+e(θ)sinδ(θ)[-bsinα+csinβ].

(5)

为使式(5)只含有圆度误差，必须使包含回转误差的项为零，即适当选择参数使：

1+bcosα+ccosβ=0，-bsinα+csinβ=0.

解得b、c分别为：b=-sinβ/sin(α+β)，c=-sinα/sin(α+β)。这样就得到只包含圆度误差的方程：

PD(θ)=s(θ)+bs(θ-α)+cs(θ+β).

(6)

实际测量为离散采样，设采样间隔为Δθ，每周采样点数N=2n=2π/Δθ，则式(6)离散化为:

PD(n)=s(n)+bs(n-m1)+cs(n+m2).

(7)

其中：m1=α/Δθ；m2=β/Δθ。设PD(n)的离散傅里叶变换为FD(k),即：

FD(k)=∑PD(n) e-j2πkn/N.

(8)

而对式(7)两边取DFT，得：

FD(k)=FS(k)+bFS(k)e-jnα+cFS(k)ejnβ.

(9)

其中:FS(k)为s(n)的DFT。则由式(9)得：

FS(k)=FD(k)/(1+be-jnα+cejnβ).

(10)

令W(k)=1+be-jnα+cejnβ，称其为权函数。由式(10)得：

FS(k)=FD(k)/W(k).

(11)

对FS(k)取傅里叶反变换，即可得圆度误差序列：

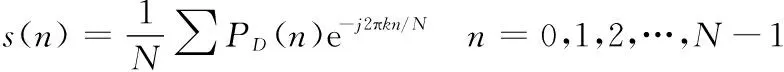
(12)

3.2 圆度误差的最小二乘评定法数学模型

如图4所示，以采样时的回转中心O1为极点建立极坐标系。令最小二乘圆的圆心为O，最小二乘圆的半径为R，最小二乘圆心O对采样时的回转中心O1偏离(偏心)为e，各离散采样点Pi(i=1,2,…,m)到最小二乘圆沿最小二乘圆半径方向的偏差为εi，θi=2π(i-1)/m。图4中，ri=O1Pi，OD=R，PiD=εi，OO1=e，∠PiO1ρ=θi，∠O1Oρ=α,Δri为各点半径差的测量值 。经过一系列的推导可以得到最小二乘圆的圆心坐标值为:

(13)

最小二乘圆半径方向的偏差为：

εi=Δri-ΔR-acosθi-bsinθii=1,2,…,m.

(14)

于是最小二乘评定法的圆度误差为[5]:

f=max{εi}-min{εi}=max{Δri-acosθi-bsinθi}-min{Δri-acosθi-bsinθi}.

(15)

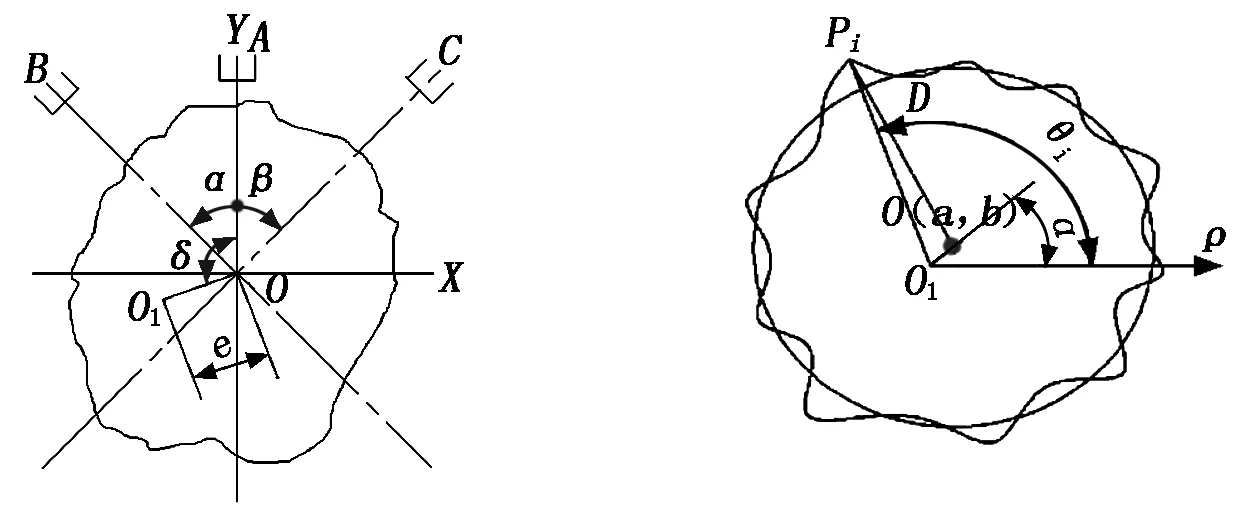
图3 三点法圆度测量原理 图4 最小二乘圆度误差评定示意图

3.3 误差分离程序与最小二乘法评定圆度设计框图

根据误差分离三点法圆度测量与误差分离技术的原理与数学模型，基于MATLAB[6]圆度误差分离的计算软件设计框图如图5所示，最小二乘法评定圆度误差的软件设计程序框图如图6所示。

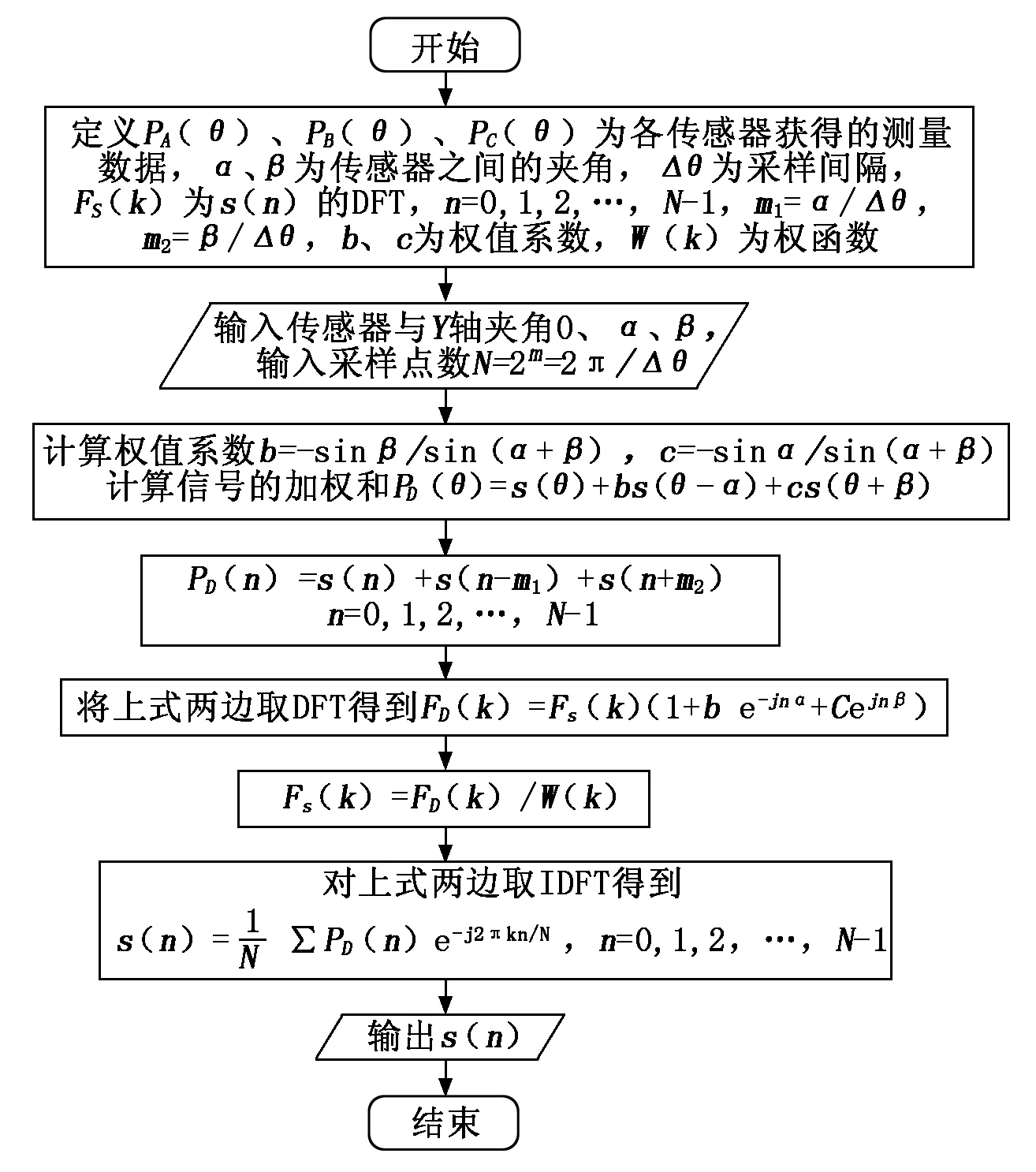
图5 圆度误差分离程序框图

4 软件程序验证

本次验证数据是在型号为Mazak Integrex 200Y/200SY的加工中心上测量的，被测件固定在加工中心的三角卡盘上，运用加工中心的手动分度功能精确分度。采用磁力架和千分表构成测量部分，在角度为零(对应A传感器)时调节千分表读值为零，每隔11.3°测量一个值ei，一周测量32个数据；接下来在-60°(对应B传感器)、+60°(对应C传感器)作起始点分别测两组数据，三组数据对应表1修改前数据。测量数据有回到起始点不为零的现象，说明存在累积系统误差，根据封闭原则[7]对数据进行处理得到了修正的数据。修改前后数据如表1所示。

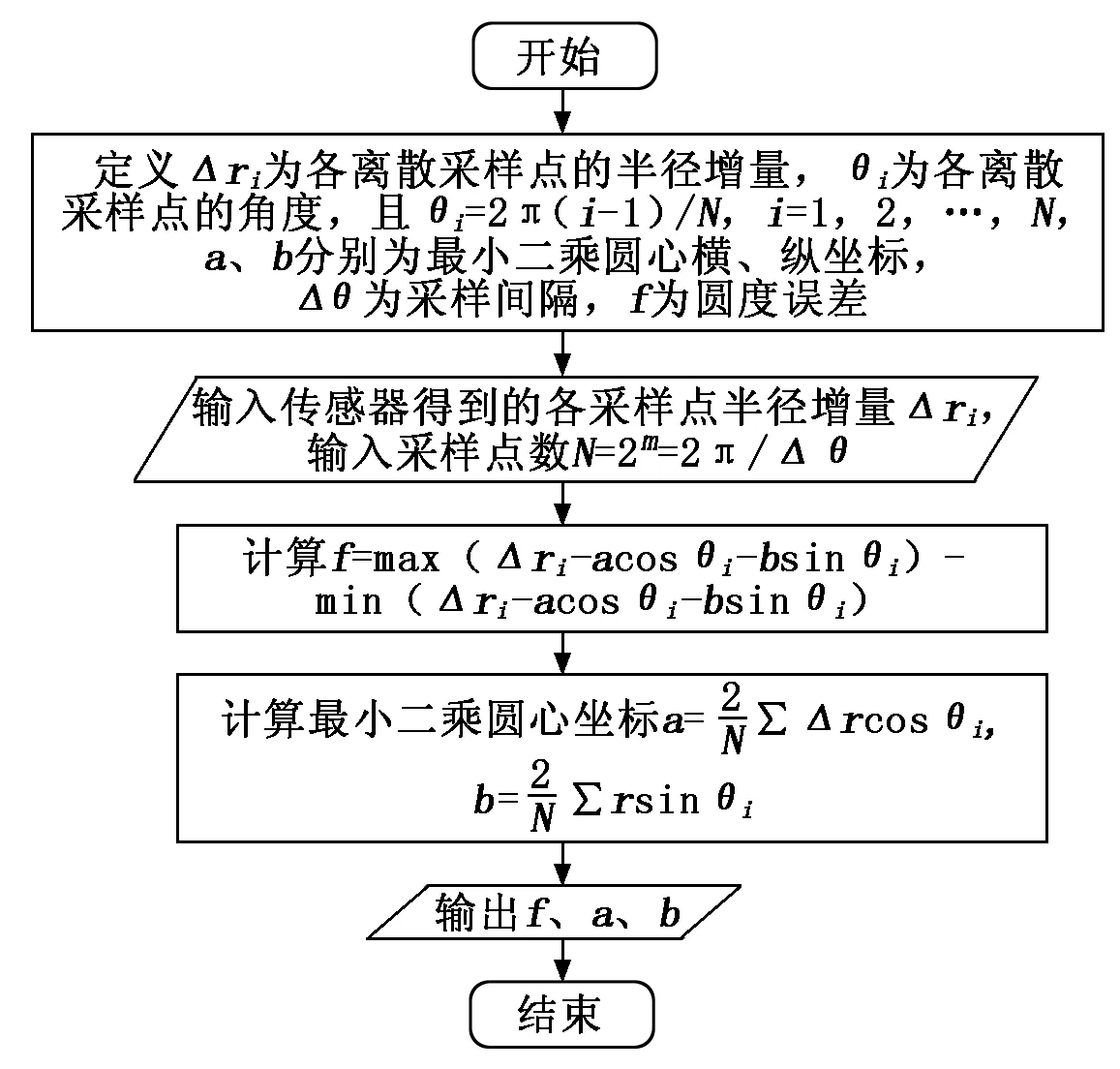
图6 最小二乘法评定圆度误差程序框图

将修正过的三组数据手动输入软件，分别对三组数据直接用最小二乘法评定，再将三组数据进行误差分离处理后用最小二乘法评定，评定结果见表2。

由表2可以看出,误差分离之后圆度误差变小了，半径偏移量e降低了将近19 μm，由此可以看出误差分离消去了系统误差。

使用本软件图形比较功能，将四种图形显示在同一个界面，可以比较出误差分离之后图形的变化，使绘制出的图形与实际相吻合，由几个最小二乘圆心也可以看出各传感器测量时的夹角。软件经过实验数据验证后，确认了其正确性。

5 结论

选用MATLAB实现了基于误差分离技术圆度误差评定测量软件的设计，该软件集计算、绘图、参数显示为一体。并进行了验证数据的实验采集、分析处理，评定结果与图形显示均表明本课题设计软件的正确性。

设计中依旧有一些不足，比如多窗体传值、数值的继承等方面很难满足工程实际对良好人机界面的需求，界面设计不如VB方便美观。下一步将探讨将MATLAB与Visual Basic混合编程[9]，使其既具有复杂的计算功能又能具有友好的界面功能。

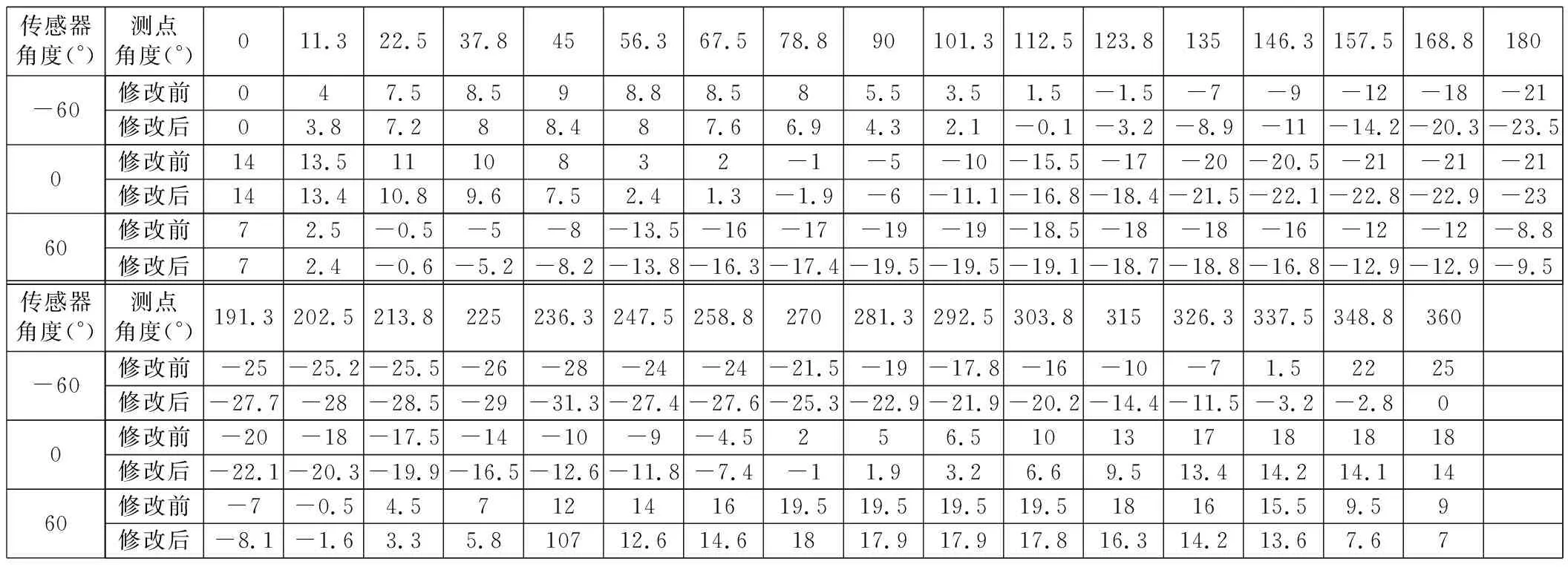
表1 修改前后实验测得的ei μm

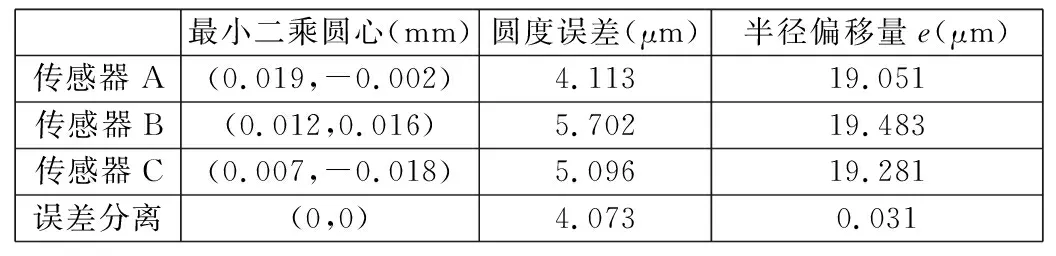
表2 实验数据显示数值

参考文献：

[1] 谭深.三点法测量圆度、轴跳动数据处理方法的商榷[J].振动测试与诊断，1986(1):3-6.

[2] 曹麒祥，王丙甲.圆度检测技术[M].北京：国防工业出版社，1998.

[3] 崔绍良.圆度测量的误差分离及数据处理[J].北京科技大学学报，1995(6)：23-26.

[4] 李圣怡，戴一帆.精密和超精密加工在位检测与误差分离技术[M].长沙：国防科技大学出版社，2008.

[5] 机械科学研究院,北京计量科学研究所.GB/T 7235—2004评定圆度误差的方法 半径变化量测量[S]. 北京：中国标准出版社，2004：1-20.

[6] 阮沈勇，王永利，桑群芳.MATLAB程序设计[M].北京：电子工业出版社，2004.

[7] 李岩，花国梁.精密测量技术[M].北京：中国计量出版社，2011.

[8] 白康生.Visual Basic程序设计[M].北京：清华大学出版社，2002.

[9] 李娜.五种VB与MATLAB混合编程接口的方法[OB] [2017-04-28].https://wenku.baidu.com/view/c0c511165bcfa1c7aa00b