一种利用水平截面法分析高压线塔倾斜度的误差模型
蔡来良,王姗姗,袁广林,谷淑丹,宋德云
(1. 河南理工大学测绘与国土信息工程学院,河南 焦作 454003; 2. 中国矿业大学力学与土木工程学院,江苏 徐州 221116)
高压线路为国民生产的能源生命线,研究线路的安全运行具有重要的现实意义。线塔架设在野外,易受大风、不稳定地质环境、地下开采等影响,引发坍塌事故。在线路运行期间对线塔开展变形监测,对防止事故发生有重要意义。
高压线塔为复杂钢结构构筑物,其形变过程具有复杂性和三维整体性的特点[1-3],同时高压线塔为高耸带电作业构筑物,在运行期塔体上布置测点和传感器具有一定难度,需要非接触测量技术的介入。地面三维激光扫描(terrestrial laser scanner,TLS)技术具有非接触测量、数据获取速度快、精度高等特点,对于快速获取高压线塔整体空间信息,依据所获取的点云数据实现三维变形的测量与分析研究,有较大优势。文献[4]阐述了输电线路的多种遥感监测方法,并对机载三维激光扫描法和地面移动三维激光扫描法进行了详细论述。文献[5]对输电线路中的高压线塔进行扫描并建立了铁塔结构分析的有限元模型。文献[6]基于高压线塔的结构特征和点云数据特点,将电力塔分为塔腿、塔身和塔头3部分,采用水平截面分层和模型驱动的方法实现了高压线塔的自动建模。文献[7]采用三维激光扫描技术监测采空区上方高压线塔,利用点云数据求取偏差对高压线塔进行倾斜度分析,但未深入分析该方法的系统误差。
高压线铁塔结构特殊,地表接触面积较小,由地表移动作用于高压线塔后产生的变形形式分为倾斜、下沉和水平位移等[8]。其中,倾斜度作为最能反映高压线塔变形情况的指标之一,对研究高压线塔倾斜度的监测方法具有极其重要的意义。基于三维激光扫描技术及其获取的点云数据分析高压线塔变形量虽然具有信息全面、三维信息精度高等优点,但点云数据量大、拓扑性差、数据分析难度较高。对高压线塔点云数据采用水平分层处理,再分析各个横截面中心与基础中心的偏移量,进而分析高压线塔倾斜度,具有思路明确、易于计算机编程实现的优点。但高压线塔为下宽上窄的竖直方向非对称结构,当其倾斜后,水平截面法获得截面中心与塔体中轴线存在一定的偏差,导致利用截面中心在竖直方向的偏移量求取的倾斜值与真值存在一定的系统偏差。本文主要介绍水平截面法,分析高压线塔倾斜值的原理,详细分析该方法产生的系统误差,建立纠正该系统误差的数学模型,并结合煤矿开采沉陷区高压线塔的监测数据对算法进行实例验证。
1 水平截面法计算高压塔倾斜度的原理
1.1 监测原理
高压线塔通常是采用焊接或螺栓连接的方法按照一定结构规则将基本构件组合而成,总体为杆柱状。水平截面法[7]求取线塔倾斜示意图如图1所示。图1中OA线段为水平截面中心点的连线,OA′线段为OA在水平面的投影。

图1 水平截面法求取高压线塔倾斜示意图
1.2 高压线塔倾斜度的计算
每期监测的高压线塔点云数据量在千万以上,数据处理过程复杂、花费时间长。采取分层处理的方式减少数据量,可达到简化数据量与保留线塔形变特征的目的。选取塔身部分按照固定步长和切片厚度进行分层处理,步长和切片厚度可根据点云密度调节。由高压线塔的结构可知,每层切片在XY平面的投影为近似矩形。采用边界提取算法提取每层切片边缘,拟合矩形四边线并计算每层切片点云的中心位置。分别令4个塔脚中心为A、B、C、D,取4个塔脚的中心值O作为底层中心。将水平截面层中心在XY平面的投影点与底层中心的距离作为每层面片的水平偏移值,根据国家电网公司企业标准《输电线路杆塔倾斜监测装置技术规范》(Q/GDW 559—2010)杆塔倾斜计算方法计算每层面片的倾斜度
G=E/H×100%
(1)
式中,G为倾斜度;E为倾斜后面片中心水平偏移距离;H为水平截面对应的塔高。计算出每层面片中心偏移值后,便可进一步求取线塔倾斜的主方向OA′方向。倾斜误差改正数的计算将在包含高压线塔倾斜主方向的AOA′竖直剖面内展开。本文将AOA′竖直剖面定义为主倾斜剖面。水平截面法求取线塔倾斜值数据处理流程如图2所示。
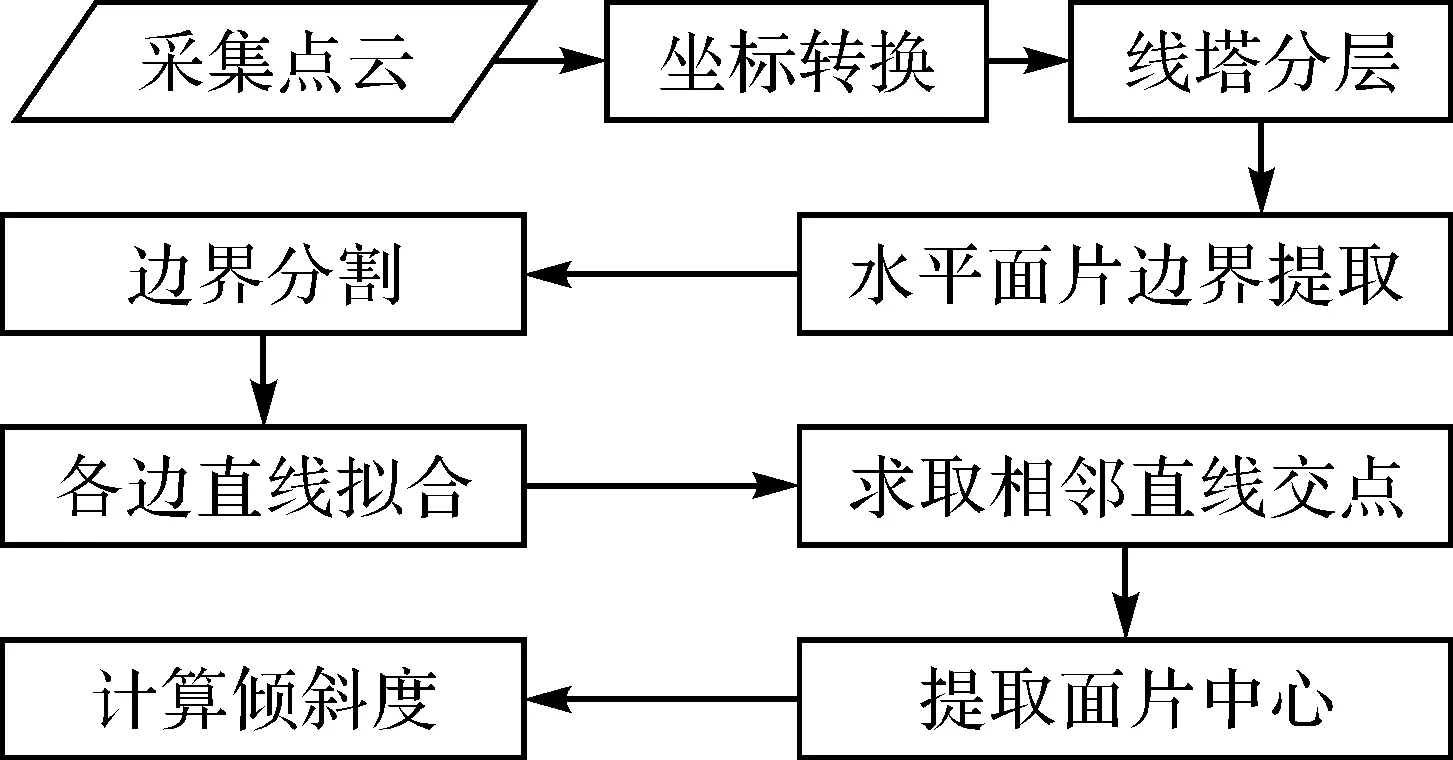
图2 水平截面法数据处理流程
上述流程中,通过点云采集步骤获取高压线塔整体三维数据,扫描时在线塔的四周架设多个站点采集数据,并将各个站点数据通过Riscan软件进行坐标转换拼接、噪声剔除、人工交互,获得完整塔体点云(如图3(a)所示)。由于塔头分支部分点云较为复杂,采用高程阈值法将其去除,再对获得的塔身点云进行水平截面法分层(如图3(b)所示),对于每分层点云采用α-shapes算法[9]提取层边界(如图3(c)所示),运用Hough变换[10-14]分割出四边点云(如图3(d)所示),再对各边点云运用稳健最小二乘法[15]拟合直线,并求出相邻直线交点如图3(e)所示,最后对每分层的4个交点求取其重心,即达到求取水平面片中心的目的。根据各层中心相对线塔基础中心的偏移量即可求得线塔倾斜度。
2 系统误差来源
在主倾斜剖面上,线塔轮廓近似为梯形,如图4所示。线塔的中轴线为CO,线塔未倾斜时的状态如图4(a)所示,倾斜后如图4(b)所示,在线塔点云中截取水平分层如图4(c)所示,求出水平分层的中点为P、Q,如图4(d)所示,连接P、Q,求出水平截面中心连线CO′如图4(e)所示,CO中轴线的倾斜值为待求真值,CO′与CO之间有一个夹角∠OCO′,该夹角为水平截面法求取线塔倾斜值的系统误差。该误差量与线塔的倾斜量及塔顶和塔基上下的非对称特性有较大关系。

图3 水平截面法数据处理效果

图4 系统误差来源示意图
3 系统误差的计算
3.1 计算模型的建立
在主倾斜剖面内,将梯形线塔轮廓的两腰向上延伸,相交于C点,C点与梯形的底构成一个近似等腰三角形,系统误差的求取在等腰三角形内展开。不论高压线塔有多少个水平分层,每层面片倾斜度的改正数计算原理均相同,计算模型如图5所示。

图5 计算模型示意图

3.2 误差计算公式的推导
3.2.1 主倾斜剖面的获取
在计算出每层面片中心后,将其中心点投影到水平面,投影点坐标为(xi,yi),其中i=1,2,…,N。运用该投影点,在水平面内可拟合出一条直线(直线方程:y=a+bx;b为斜率,a为截距,计算方法见式(2)),由直线的斜率可求出主倾斜剖面的延伸方向(图1中AOA′平面)。
(2)
3.2.2 倾斜误差计算
(3)

由式(4)得到
β=M-α
(4)
在经△AiBiAi0中
(5)
式中,Y为高压线塔轮廓线投影与基底面投影线的夹角;D为基底面投影线的长度。
(6)
得
(7)
令tanα=x,tanM=t,tanY=2H/D,得
4H2tx2+(D2+4H2)x-D2t=0
(8)
解算关于x=tanα(α∈[0,90°),tanα>0)的一元二次方程
Δ=(D2+4H2)2+16D2H2t2
当t=0时,x=0,即当未倾斜时,倾斜角为0,改正数为0;当t≠0时,x的解为
(9)
3.2.3 倾斜度及误差计算的实现
利用三维激光扫描仪采集的高压线塔点云数据,数据量大,国内外暂无成熟的形变分析软件可用,因此本文利用自编程序实现分层处理、倾斜度计算和误差改正。
4 工程实例
试验区域位于山西矿区,由于地下采矿引起地表沉陷,导致高压线塔倾斜。采集数据时研究对象已经发生倾斜。试验使用的仪器为Riegl VZ-1000三维激光扫描仪,100 m距离处依次单点扫描精度为5 mm,扫描视角为100°*360°(垂直*水平),能够满足对高压线塔分析的精度需要。在高压线塔周围布设多站,以实现高压线塔的多方位测量。对采集的点云数据进行滤波、去噪、分类等处理后,获取高质量的高压线塔点云数据。利用项目组开发的点云处理程序实现高压线塔面片中心的提取,完成高压线塔倾斜度的计算。数据采集及处理如图6所示,计算结果见表1。

图6 研究对象影像、点云及水平截面边界
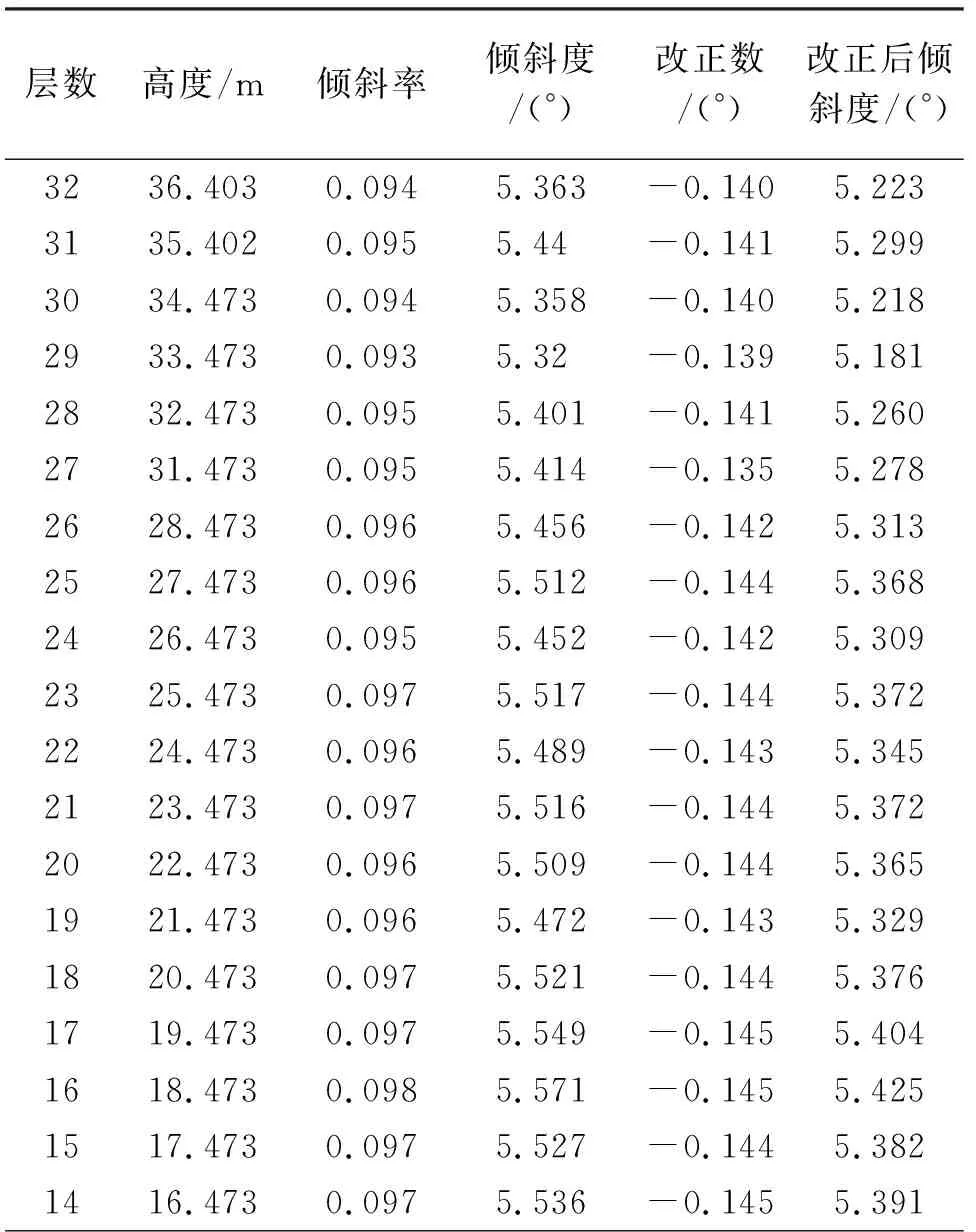
层数高度/m倾斜率倾斜度/(°)改正数/(°)改正后倾斜度/(°)3236.4030.0945.363-0.1405.2233135.4020.0955.44-0.1415.2993034.4730.0945.358-0.1405.2182933.4730.0935.32-0.1395.1812832.4730.0955.401-0.1415.2602731.4730.0955.414-0.1355.2782628.4730.0965.456-0.1425.3132527.4730.0965.512-0.1445.3682426.4730.0955.452-0.1425.3092325.4730.0975.517-0.1445.3722224.4730.0965.489-0.1435.3452123.4730.0975.516-0.1445.3722022.4730.0965.509-0.1445.3651921.4730.0965.472-0.1435.3291820.4730.0975.521-0.1445.3761719.4730.0975.549-0.1455.4041618.4730.0985.571-0.1455.4251517.4730.0975.527-0.1445.3821416.4730.0975.536-0.1455.391

续表1
水平截面法的倾斜角改正数主要与线塔的倾斜量与Y角有关。线塔的倾斜值越大,改正数越大,Y角越小,改正数越大。为了更加清楚地表达改正数的变化情况,分析其影响因素,从下向上为层数编号,改正数与高度和倾斜率的关系如图7所示,从图中可以看出,改正数的变化曲线基本与倾斜度的变化曲线走势相同。说明该线塔上下部分的倾斜值较一致,线塔虽然发生了较大倾斜量(大于5°),但上下倾斜量较均匀,弯曲度较小。

图7 倾斜度与改正数关系
为了验证改正后偏差度的准确性,将获取的点云数据导入RiScan软件中,先选定高压线塔最高处的四棱点,以下沉最大的棱为基准,确定该棱对应的最高点与最高层面片的距离,选定四棱上在该高度处的特征点。该步骤是为了确定选取的该高度处的平面垂直于高压线塔的中心线,即与倾斜后高压线塔最高面平行。然后在四条棱上向下以相同的距离确定各个棱边的特征点,以此特征点沿各棱边向下依次间隔1 m在高压线塔的四棱中选取特征点,直至高压线塔底,确保相对高度处特征点所组成的平面均与倾斜后高压线塔中心线垂直。在点云中选取的特征点示意图如图8所示。连接高压线塔四棱边依次相对应的特征点计算出相应的每层面片高度处的中心,与最底层的中心作对比,并计算得到倾斜率。试验中选取3~37 m之间的面片进行验证,结果对比见表2。

图8 手工选取特征点示意图
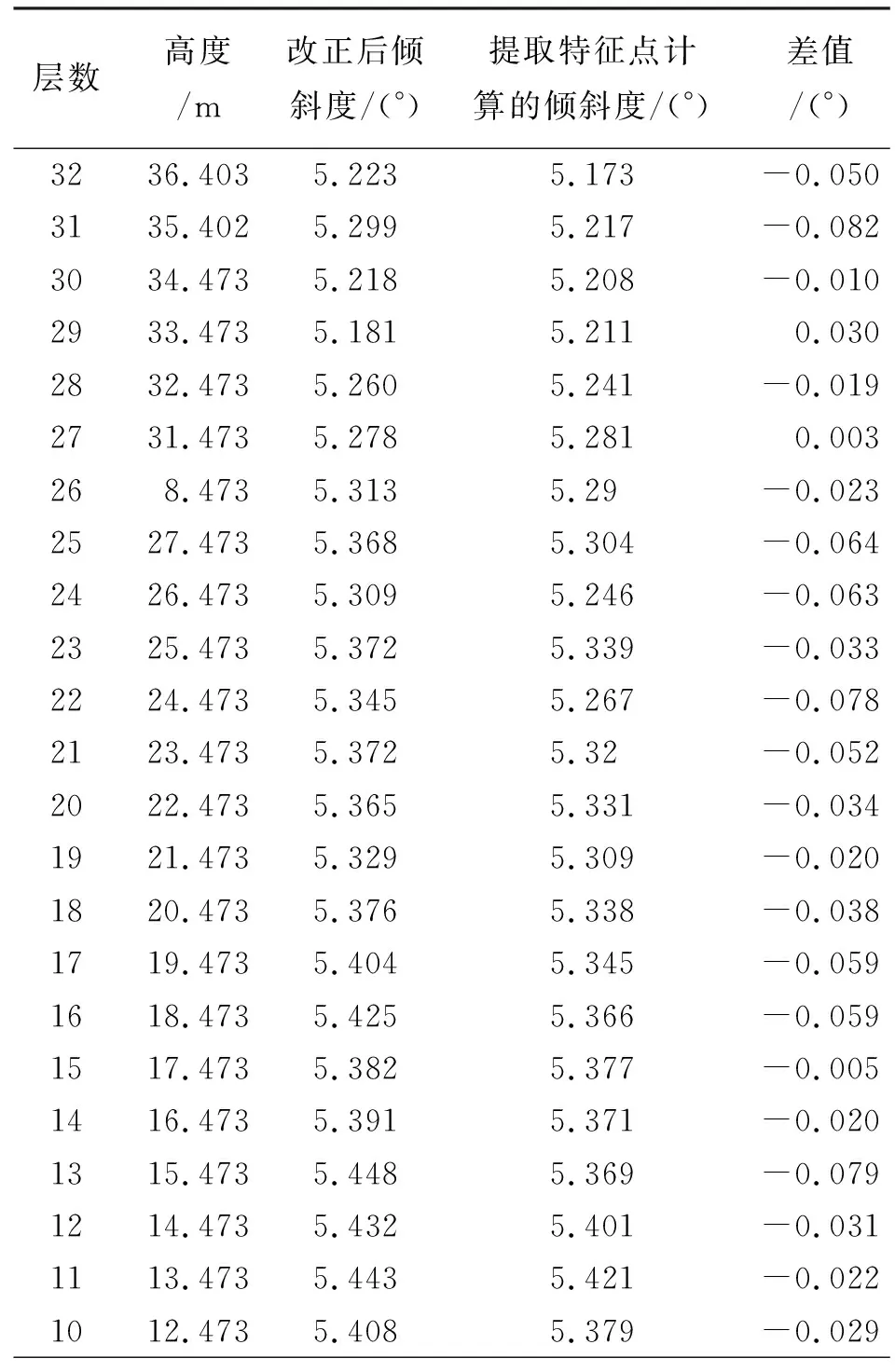
层数高度/m改正后倾斜度/(°)提取特征点计算的倾斜度/(°)差值/(°)3236.4035.2235.173-0.0503135.4025.2995.217-0.0823034.4735.2185.208-0.0102933.4735.1815.2110.0302832.4735.2605.241-0.0192731.4735.2785.2810.003268.4735.3135.29-0.0232527.4735.3685.304-0.0642426.4735.3095.246-0.0632325.4735.3725.339-0.0332224.4735.3455.267-0.0782123.4735.3725.32-0.0522022.4735.3655.331-0.0341921.4735.3295.309-0.0201820.4735.3765.338-0.0381719.4735.4045.345-0.0591618.4735.4255.366-0.0591517.4735.3825.377-0.0051416.4735.3915.371-0.0201315.4735.4485.369-0.0791214.4735.4325.401-0.0311113.4735.4435.421-0.0221012.4735.4085.379-0.029

续表2
计算误差改正数的过程中,高压线塔棱柱倾斜度和面片所在三角形底边的获取直接影响计算过程和计算精度。从表2中可以看出,改正后的倾斜度与手动选取特征点计算出的倾斜度更加接近,改正数的大小与高度、高压线塔的倾斜度和高压线塔自身的结构有关,它们之间具有非线性函数关系。对利用水平截面法计算获得的倾斜度加入误差改正数,使倾斜度计算的误差从“度”降到“分”,能有效地提高面片法倾斜度计算的精度。
根据计算结果采用沿主倾斜方向的反方向设置多条钢拉索纠偏的方法处理线塔,防止线塔倾斜姿态进一步恶化,保障了输电线路顺利运行。
5 结 语
本文分析了基于三维激光扫描技术监测高压线塔倾斜量的点云水平分层截面法,通过对其原理的分析,发现了该方法存在的系统误差,建立了误差计算模型。应用实例数据对误差计算模型进行了验算,确定了误差改正数计算模型的可靠性,并与手工选取特征点计算的倾斜度进行对比,验证了该系统误差计算方法的准确性,确定了计算精度。误差改正数的加入,提高了水平截面法计算倾斜量的准确度。本文的研究为基于激光雷达的高压线塔高精度监测技术开发奠定了基础。
参考文献:
[1] 李鹏云,陈波,张峰,等.输电钢塔结构支座的沉降监测与模拟[J].光学精密工程,2013,7(1):68-71.
[2] XIAO Zhenzhong,LIANG Jin,YU Dehong,et al.Rapid Three-dimension Optical Deformation Measurement for Transmission Tower with Different Loads[J].Optics and Lasers in Engineering,2010,48(9):869-876.
[3] 李清泉,李必军,陈静.激光雷达技术及其应用研究[J].武汉测绘科技大学学报,2000,25(5):387-391.
[4] MATIKAINEN L,LEHTOMKI M, AHOKAS E,et al.Remote Sensing Methods for Power Line Corridor Surveys[J].ISPRS Journal of Photogrammetry and Remote Sensing,2016,119 (2016):10-31.
[5] CONDE B,VILLARINO A,CABALEIRO M.Geometrical Issues on the Structural Analysis of Transmission Electricity Towers Thanks to Laser Scanning Technology and Finite Element Method[J].Remote Sensing,2015,7 (9):11551-11569.
[6] LI Q,CHEN Z,HU Q.A Model-driven Approach for 3D Modeling of Pylon from Airborne LiDAR Data [J].Remote Sensing,2015,7 (9):11501-11524.
[7] 刘云备,蔡来良,杨望山,等.基于TLS的高压线塔倾斜度监测[J].测绘工程,2016,25(8):65-69.
[8] 郑彬.采动影响下高压输电线路铁塔的安全性研究[D].焦作:河南理工大学,2009.
[9] 沈蔚,李京,陈云浩,等.基于LIDAR数据的建筑轮廓线提取及规则化算法研究[J].遥感学报,2008,12(5):692-698.
[10] OVERBY J,BODUM L,KJEMS E.et al.Automatic 3D Building Reconstruction from Airborne Laser Scanning and Cadastral Data Using Hough Transform[J].Remote Sensing,2004,35(B3):296-301.
[11] TARSHA-KURDI F,LANDES T,GRUSSENMEYER P.Hough-transform and Extended Ransac Algorithms for Automatic Detection of 3D Building Roof Planes from Lidar Data[C]∥Proceedings of ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007.Espoo,Finland:[s.n.],2007:407-412.
[12] TORRENTE M L,BIASOTTI S,FALCIDIENO B.Recognition of Feature Curves on 3D Shapes Using an Algebraic Approach to Hough Transforms[J].Pattern Recognition,2017,51 (1):1-20.
[13] 张帆,高云龙,黄先锋,等.基于球面投影的单站地面激光点云直线段提取方法[J].测绘学报,2015,44(6):655-662.
[14] 李畅,李芳芳.基于假设检验的数字影像线状特征亚像素自动提取[J].测绘学报,2013,42(1):67-72.
[15] RENNER R M.A Constrained Least-squares Subroutine for Adjusting Negative Estimated Element Concentrations to Zero[J].Computer and Geosciences,1993,19(9):1351-1360.