多路径原子干涉仪的动力学研究
何天琛
(太原师范学院 物理系, 山西 晋中 030619)
最近20年, 原子物质波在量子光学和原子物理学中的干涉现象引起了人们的广泛关注. 利用物质波的干涉特性, 人们设计了各种各样的原子干涉仪[1-3]. 第一台原子干涉仪[4]使用衍射光栅实现了分束器和复合器, 且可以使分开的原子波包发生相干叠加进而获得相移. 其它的原子干涉仪[5-6]也使用了类似的装置来获得相移. 从第一台原子干涉仪开始, 它们在推进物理学发展中一直起着非常重要的作用.
原子和光在物理特性上有本质的不同, 在测量惯性力上, 原子干涉仪比传统的光学干涉仪要灵敏得多. 通过分束器和镜像操作, 原子干涉仪可以用来测量重力加速度[7-12]. 其原因是原子物质波可以与重力场发生耦合. 此外原子干涉仪在精密惯性传感器[13], 测量物理常数[14]和其它的基本研究中[15]也起到了非常关键的作用.
对于冷原子而言, 实验上使用Kapitza-Dirac脉冲[16], 在谐振子势阱中使冷原子发生了干涉现象且在演化过程中保持了较好的相干性[17]. 基于冷原子可以和外场发生相互作用. 多路径干涉仪[18]利用谐振子势阱中的冷原子和Kapitza-Dirac脉冲来测量外场. 在这套干涉仪方案中, Kapitza-Dirac脉冲起着类似经典光学干涉仪分束器的作用. 谐振子势阱则可以使原子束在分开之后再次相干叠加. 本文采用传播子的方法解析计算系统含时演化波函数的一般解, 分析比较有外场和无外场情况下的态密度演化规律, 阐明外场影响系统动力学的内在物理机制.
1 多路径原子干涉仪模型
在t=0时, 给基态原子作用第一次Kapitza-Dirac脉冲VKD(x)=V0Erδtcos(kx).V0为脉冲的强度,Er为反冲能量,k=4π/λ,λ为激光的波长,δt为脉冲的持续时间. 第一次Kapitza-Dirac 脉冲把初始波包劈裂成许多具有不同动量的波包, 且在外场Vα=αx中开始沿不同的路径演化. 在t=τ时, 所有的波包在谐振子势阱的作用下相干叠加. 第二次Kapitza-Dirac 脉冲再次把叠加的波包分开. 在t=3τ/2, 通过测量原子的态密度分布函数, 可以得出外场的强度. 如图 1 所示.
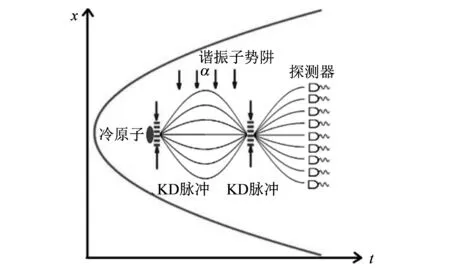
图 1 多路径原子干涉仪示意图Fig.1 Diagram of multipath atom interferometer
2 多路径原子干涉仪的动力学过程
2.1 第一次Kapitza-Dirac 脉冲
本文将采用传播子的方法来解析计算系统的含时波函数. 在t=0时刻, 给基态的冷原子加第一次Kapitza-Dirac脉冲, 有
ψ(x,0)=ψ(x,0)exp(-iVcos(kx))=
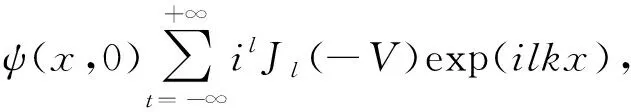
(1)
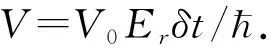
接下来, 原子在谐振子势阱Vh和外场Vα的共同作用下演化, 通过传播子积分可以得到系统实空间的含时波函数为
ψ(x,α,Δt)=
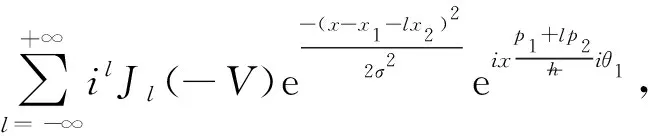
(2)
且有
x2=kσ2sin(ωΔt),
这里, Δt为外场的持续作用时间且有0≤Δt≤τ.
K为谐振子势阱中的传播子
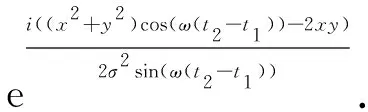
(3)
ψ(p,α,Δt)=
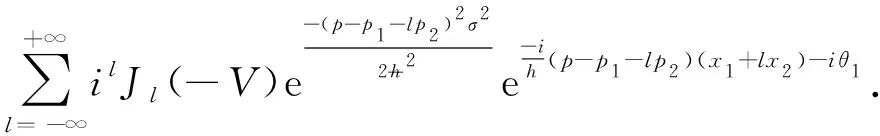
(4)
在方程(4)中, 波包动量空间的整体相位相对于实空间没有改变. 动量空间波包的幅度值仍然由贝塞尔函数来决定.
2.2 第二次Kapitza-Dirac脉冲
当原子演化到t=τ时, 给系统加第二次Kapitza-Dirac脉冲, 然后原子在没有外场的情况下演化到任意时刻t, 再次使用传播子, 系统在实空间的波函数为
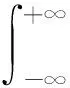
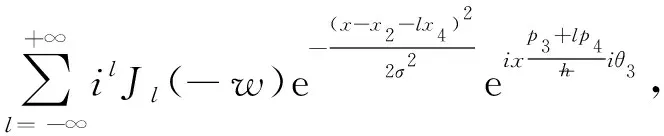
(5)
和
x4=-kσ2sin(ωt),
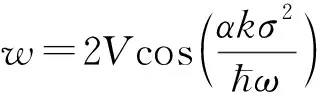
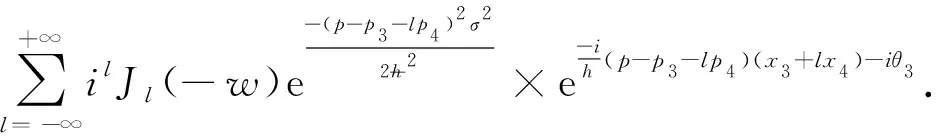
(6)
3 多路径原子干涉仪的态密度演化规律
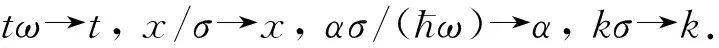
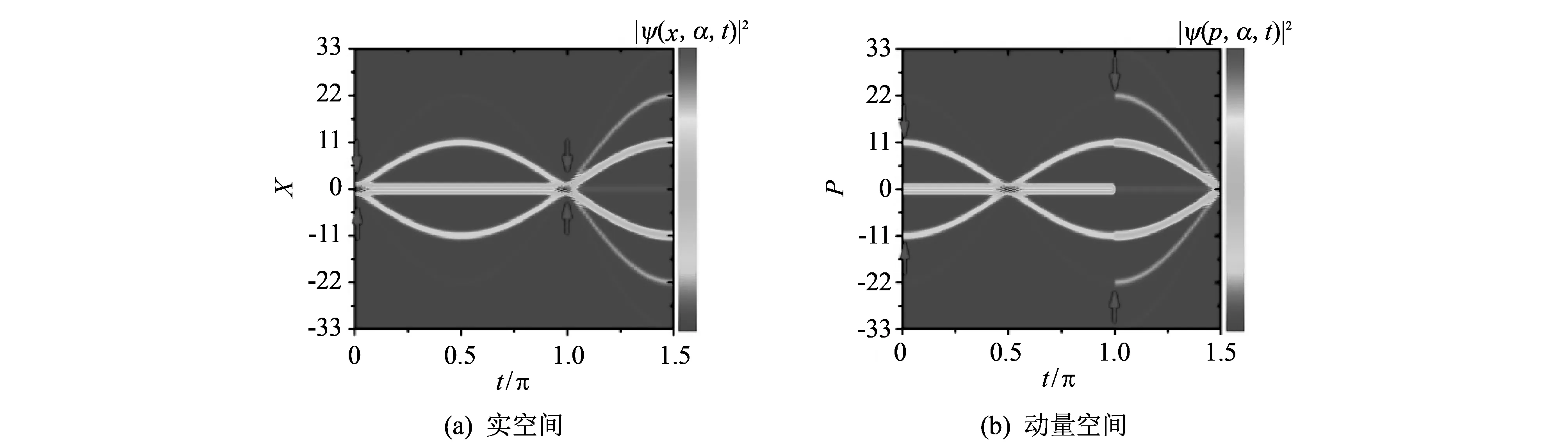
图 2 没有外场情况下系统的态密度随时间的演化规律Fig.2 Time evolution of density distribution without external field

图 3 存在外场情况下系统的态密度随时间的演化规律Fig.3 Time evolution of density distribution with external field
4 结 论
本文在实空间和动量空间研究了多路径原子干涉仪的动力学过程. 基于传播子的方法, 解析计算出了任意时刻系统态密度的分布规律. 通过对态密度含时演化过程的分析,相对于没有外场的态情况. 计算结果表明, 外场决定了实空间波包和动力空间波包的演化路径, 让波包在实空间和动量空间以正弦和余弦的函数形式演化. 测量时刻外场的信息仅仅出现在波包的幅度中.
参考文献:
[1] 陈乐乐, 罗覃, 邓小兵, 等. 基于原子干涉技术的精密重力测量研究[J]. 中国科学: 物理学、 力学、 天文学, 2016, 46(7): 21-38.
Chen Lele, Luo Qin, Deng Xiaobin, et al. Precision gravity measurements with cold atom interferometer[J]. Sci Sin-Phys Mech Astron, 2016, 46(7): 21-38. (in Chinese)
[2] 许翱鹏, 王兆英, 王启宇, 等. 原子重力仪的共模噪声抑制研究[J], 物探与化探, 2015, 39 (S1): 58 -62.
Xu Aopeng, Wang Zhaoying, Wang Qiyu, et al.The restraint of the common-mode noise in the cold atom gravimeter[J]. Geophysical and Geochemical Exploration, 2015, 39 (S1): 58-62. (in Chinese)
[3] 翟振和, 吴富梅. 基于原子干涉测量技术的卫星重力梯度测量[J]. 测绘通报, 2007(2): 5-7.
Zhai Zhenhe, Wu Fumei. Satellite gravity gradiometry based on atominterferometry technique[J]. Bulletin of Surveying and Mapping, 2007(2): 5-7. (in Chinese)
[4] Keith D W, Ekstrom C R, Turchette Q A, et al. An interferometer for atoms[J]. Phys. Rev. Lett., 1991, 66(21): 2693-2696.
[5] Rasel E M, Oberthaler K M, Batelaan H, et al. Atom wave interferometry with diffraction gratings of light[J]. Phys. Rev. Lett., 1995, 75(14): 2633-2637.
[6] Giltner D M, McGowan R W, Lee S A , et al. Atom interferometer based on bragg scattering from standing light waves[J]. Phys. Rev. Lett., 1995, 75(14): 2638.
[7] McGuirk J M, Foster G T, Fixler J B, et al. Sensitive absolute-gravity gradiometry using atom interferometry[J]. Phys. Rev. A, 2002, 65(3): 033608.
[8] Fixler J B, Foster G T, McGuirk J M, et al. Atom interferometer measurement of the newtonian constant of gravity[J]. Science, 2007, 315(5808): 74-77.
[9] Roati G, Mirandes E D, Ferlaino F, et al. Atom interferometry with trapped fermi gases[J]. Phys. Rev. Lett., 2004, 92(23): 230402.
[10] Ferrari G, Poli N, Sorrentino F, et al. Long-lived bloch oscillations with bosonic Sr atoms and application to gravity measurement at the micrometer scale[J]. Phys. Rev. Lett., 2004, 97(6): 060402.
[11] Poli N, Wang F Y, Tarallo M G, et al. Precision measurement of gravity with cold atoms in an optical lattice and comparison with a classical gravimeter[J]. Phys. Rev. Lett., 2011, 106(3): 038501.
[12] Tarallo M G, Alberti A, Poli N, et al. Delocalization-enhanced bloch oscillations and driven resonant tunneling in optical lattices for precision force measurements[J]. Phys. Rev. A, 2012, 86(3): 033615.
[13] Peters A, Chung K Y, Chu S, et al. High-precision gravity measurements using atom interferometry[J]. Metrologia, 2001, 38(1): 25-61.
[14] Wicht A, Hensley J M, Sarajlic E, et al. A preliminary measurement of the fine structure constant based on atom interferometry [J]. Physica Scripta, 2002(T102): 82.
[15] Rosi G, Sorrentino F, Cacciapuoti L, et al. Precision measurement of the newtonian gravitational constant using cold atoms [J]. Nature (London), 2014(510): 518-521.
[16] Keller C, Schmiedmayer J, Zeilinger A, et al. Adiabatic following in standing-wave diffraction of atoms[J]. Applied Physics B, 1999, 69(4): 303-309.
[17] Sapiro R E, Zhang R, Raithel G, Atom interferometry using Kapitza-Dirac scattering in a magnetic trap[J]. Phys. Rev. A, 2009, 79(4): 043630.
[18] Li W D, He T C and Smerzi A, Multimode Kapitza-Dirac interferometry with trapped cold atoms[J]. Phys. Rev. Lett., 2014, 113(2): 023003.
[19] Olver F W J, Lozier D W, Boisvert R F, et al. NIST handbook of mathematical functions[M]. First edition. New York: Cambridge University Press, 2010.

