重视数学思想方法，搞好数学活动课教学

曾珍 洪复龙

前不久，笔者参加江西省优秀青年教师助力项目——初中数学同课异构研讨活动。在活动中，两位教师针对人教版《数学》七年级上册“月历上的数学”这一课题，以同课异构的方式分别上了一节数学活动课。本文将以两位教师的教学设计为基础，围绕着数学活动课到底要教什么、怎么教等问题进行探究与反思。

1.教师甲的教学设计

环节一 开门见山，直入主题

多媒体播放两个卡通人物的语音对话引入课题：月历中的数学问题。

品仔：“我昨晚观察11月份的月历，发现了许多奇妙的规律。”

星宝：“我也发现了许多规律！”

环节二 合作交流，探究新知

请同学们仔细观察手中的月历，要求：（1）寻找你手中月历表上的数字排列规律，至少3条；（2）小组合作，交流并寻找规律的共同点。

各小组讨论并展示成果后，教师引导学生总结得出以下规律：

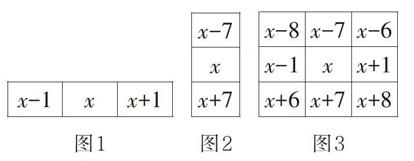
①如图1，左右相邻两个数相差1；

②如图2，上下相邻两个数相差7；

③如图3，任意圈一个九宫格，九个数字相加再除以9会等于正中间的数；

[x-1 x x+1 ][图1][x-7 x x+7 ][x-8 x-7 x-6 x-1 x x+1 x+6 x+7 x+8 ][图2][图3]

环节三 洞悉规律，学以致用

例1 已知某年某月共有4个星期一，这4天的日期之和为50，这个月的1号是星期几？

变式1：如果换成8个一排的连续正整数，上下相邻的两排数相差多少？

变式2：如果换成n个一排的连续正整数，上下相邻的两排数相差多少？

环节四 深层思考，应用升华

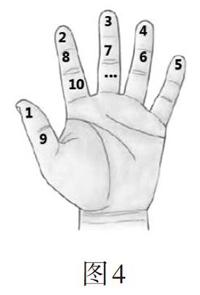
例2 如圖4，将1、2、3、4、5、6、7、8、9…在手指上按照拇指、食指、中指、无名指、小指、无名指、中指、食指、拇指、食指……依次类推排列，求：2017落在哪根手指上？

2.教师乙的教学设计

环节一 认识月历，确定主题

问题1：今天的日期是多少？（接着播放视频让学生了解历书的演变过程）

问题2：生活中的月历是什么样的？（PPT展示日历、月历、年历图片）

问题3：月历中的数学有哪些呢？（导入课题：月历中的数学）

环节二 实践活动，探索新知

活动1：请同学们完善导学案中10月份的月历表，观察自己所填的数都是些什么数字？（发现：设月历中的数字为a，则1≤a≤31且a为整数）

活动2：请同学们在准备好的月历中任意圈出行排（竖列）上相邻的3个数字，再把它们的和告诉老师，接着老师猜测具体是哪3个数。

思考：老师为什么能猜出来？如果3个数相邻，它们之间有什么规律？（发现：位于同一条线上相邻3个数字的和是中间数的3倍）

活动3：思考课本73页的问题1和问题2。（发现：方框框出的9个数字之和是正中心数字的9倍）

环节三 综合应用，拓展提升

例1 小明于2014年秋季考入重点中学。9月1日（星期一）报名并住校。如果他每周六回家一次，那么第一次回家应该是几号？第三次呢？

例2 用一个正方形框出9个数，要使9个数的和等于100，198，你是否办得到？如果办不到，简单说明理由；如果办得到，说出正方形里的最大数。

环节四 活动总结，布置作业

（1）通过这节课，我们学会了如何看待月历？

（2）探究规律，一般要经过哪些过程？

（3）如何用数学的方式来表述问题？

3.关于公开课的深入反思

在研讨活动中，各位专家及一线教师从课堂导入、探究方式、例题设计等多角度对两位教师的教学进行点评，让不同的教学理念在交流中碰撞升华，令笔者受益匪浅，也让我们反思：“月历上的数学”到底要“教什么”？要“怎么教”？

（1）“教什么”。本节数学活动课到底“教什么”，仅仅局限在探究数字间的排列规律就可以了吗？显然不是，发现给定月历中的行、列或者斜线相邻的数字间的规律对学生来说不是难事，但数学是变化万千的，其中蕴含的思想方法“万变不离其宗”。数学学习的根本目的，其实就在于掌握这种具有普遍意义和广泛迁移价值的策略性知识——数学思想方法。

类比归纳、特殊到一般是本节课比较常见的两种数学思想方法，教师通过例题可以挖掘更多的思想方法。如教师甲选择的南昌市中考模拟题——“2017落在哪根手指？”学生做这道题时仅仅依靠数手指是不能解答问题的，而是要借助表格。通过这道题的训练，学生将会意识到表格其实是一种工具，从而领悟到数形结合思想。

（2）“怎么教”。著名数学家华罗庚曾说过：“学习数学最好是到数学家的纸篓里找材料，不要只看书上的结论。”所以，教学中不能只注重最后的结果，而是要让学生经历知识的发生、发展过程，体会数学思想方法的内涵。

本节课的重点之一是“用字母表示数”，教师如果直接提问学生：“能不能先用字母表示数，再表示出月历中的规律？”学生当然能回答这个问题，但是为什么要用字母表示数呢？学生很难理解这个问题。所以，在教学时，教师应引导学生体会由特殊到一般的数学思想方法，发现用字母表示数的优越性，以培养学生的符号意识及推理能力。

（3）“教什么”永远比“怎么教”更重要。“教什么”和“怎么教”一直是教学研究的两个基本问题。“教什么”关乎教学内容问题，而“怎么教”关乎教学形式问题。教学内容决定教学形式，而教学形式服务于教学内容，所以“教什么”永远比“怎么教”更重要。

对于数学活动课的教学，有教师为追求“活”，设计出了五花八门的探究活动并安排学生小组讨论，营造了活跃的课堂气氛，但这是数学活动课真正追求的吗？我们认为不是，数学活动课不应局限在形式，而更应强调思维上的活跃。教师只有重视数学活动思维功能的发挥，挖掘隐藏于数学活动中的思想方法，学生所掌握的知识才会是生动的、鲜活的、可迁移的。