樱桃好吃树难栽方程组好列解难求

董凤娥

(河北省唐山市丰润区任各庄镇中学 064012)

一、问题的提出

匀变速直线运动问题，是初学高中物理的学生所接触的第一类重要的计算.因为受小学、初中数学中有关路程类问题的多年影响，还受初中物理学过的匀速直线运动物理问题的影响，再加上数学计算、数形结合及其空间想象能力较差等因素的制约，总有一部分人不能较好的适应新出现的“加速度”、“位移”等基本概念和有关运动学公式及其推论等对解决此类问题所起的重要作用.这就致使部分人在解答此类问题时，有一种似曾相识的感觉，可就是算不对.怎样才能突破这种“瓶颈”，达到“柳暗花明又一村”的境界呢？下面，本文以一道典型高考题为例，从物理和数学两个维度，探究这类题的解题策略.

二、探究的过程

题目(2008年全国高考理综)已知O、A、B、C为同一直线上的四点，AB间的距离为L1，BC间的距离为L2.一物体自O点由静止出发，沿此直线做匀加速运动，依次经过A、B、C三点.已知物体通过AB段与BC段所用时间相等.求O与A的距离.

解法1 应用两次位移公式和一次位移速度关系式，建立方程组.

设物体的加速度为a，经过A点时的速度为v0，经过AB段和BC段的时间为t，以物体在AB段和AC段的运动为研究对象，根据位移公式可得：

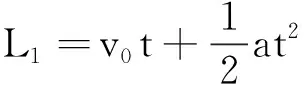
L1+L2=2v0t+2at2

②

以物体在OA段的运动为研究对象，根据位移速度关系公式得：

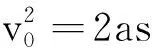
③

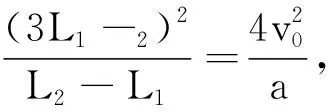
解法2 应用三次位移公式求时间，利用时间等量建立方程.

设物体运动的加速度为a，OA段位移为s，物体在OA段、OB段、OC段运动时间分别为t1、t2、t3.以物体在OA段、OB段、OC段的运动为研究对象，根据位移公式可得：

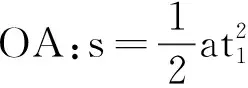
①

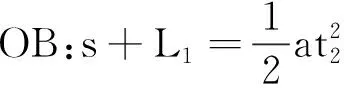
②

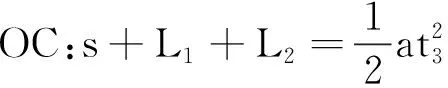
③

已知物体在AB段与BC段所用时间相等，所以有t2-t1=t3-t2成立，即：

整理可得无理方程：

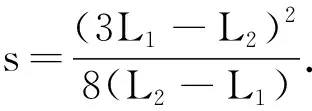
点评此解法抓住已知条件，利用物理知识导出一个方程进行求解.看似不需要较强的数学技巧，其实不然.因为在初中数学课本中，把无理方程删掉已经至少有十几年了，学生解无理方程不会一帆风顺.从这个角度来说，指导学生“掌握无理方程的解法”非常重要而且紧要.

解法3 应用三次位移公式，建立方程组.

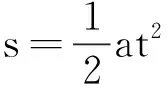
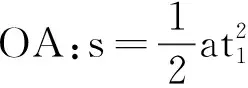
①

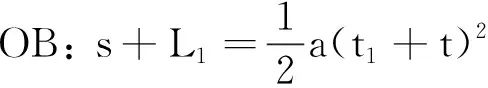
②

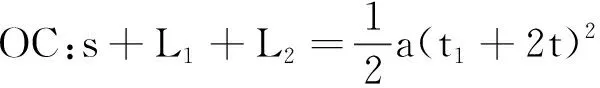
③

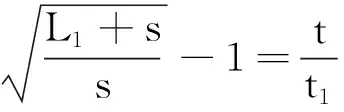
解法4 用邻等时内位移差等、位移公式和位移速度关系式，建立方程组.

设物体加速度为a，经过A点时的速度为v0，经过AB段和BC段的时间为t，利用“做匀变速直线运动的物体，在相邻相等时间内的位移之差相等”，即ΔSn+1-ΔSn=at2成立.据此可得：

L2-L1=at2

①

以物体在AC段的运动为研究对象，根据瞬时速度和位移公式可得：

L1+L2=2v0t+2at2

②

以物体在OA段的运动为研究对象，根据位移速度关系公式得：

③

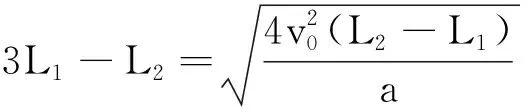
解法5 用平均速度、中时瞬时速度、邻等时内位移差等、位移速度关系式，建立方程组.

设物体的加速度为a，经过A点时的速度为v0，经过AB段和BC段的时间为t，以物体在AC段的运动为研究对象，由平均速度公式可得：

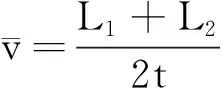
①

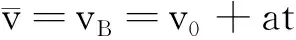
②

又因为“做匀变速直线运动的物体，在相邻相等时间内的位移之差相等”，即ΔSn+1-ΔSn=aT2成立.据此可得：L2-L1=at2

③

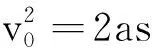
④

点评解方程组时，由①②显然可得L1+L2=2v0t+2at2⑤，接下来联立③④⑤求解，过程同解法四如出一辙.仔细品味，本解法比解法四还要高明，高明之处在于，把匀变速直线运动所涉及到的多数基本概念、基本公式，结合课本习题得到的性质、结论和推论等，完美的综合了在一起，很有物理的“味”道.真是具有“王者风范”，我们应该为之点赞.

解法6 用速度时间关系图像的几何意义和相似三角形性质，建立方程组.

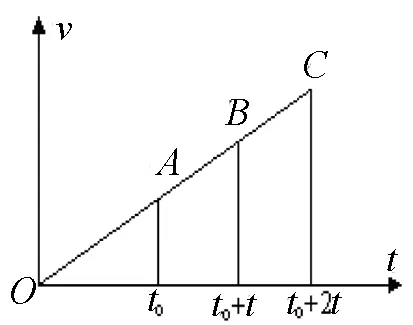
图

设物体经过A、B、C三点时，对应的时刻分别为t1、t1+t和t1+2t，则物体运动的v-t图像如图所示.根据v-t图像的物理意义可知，三角形的面积表示对应时刻位移的大小.因此，包含位移OA、OB、OC的各直角三角形的面积，分别等于位移OA、OB、OC的大小.显然三个直角三角形是相似的，根据相似三角形的面积比等于相似比的平方可得：

①

②

点评本解法有一种给人“眼前一亮”的那种感觉，非常独特.其实，它就在课本中，并且出现频率还很高，可为什么有很多人就是想不到呢？因此，掌握 图像和 图像的物理意义很重要.今天解题用到了“图像法”，明天、后天还会用到.至于方程组的解法，见解法二的点评，不再累述.

三、得出的结论

1.构建知识体系，形成思维导图

如果不考虑匀速直线运动和以后将要学习的平抛、

斜抛、自由落体、竖直上抛等运动，就目前而言，匀变速直线运动的知识主要包括：定义、特点和分类，位移和时间之间的关系，速度和时间之间的关系，位移和速度之间的关系，重要性质和推论，常用的比例关系式，等等.

把这些知识构建成一个体系，和平时做题积累的一些解题技巧融合在一起，形成“思维导图”，在头脑中不断进行存储、补充、完善和强化.只有养成这样的好习惯，今后解题时，才能迅速从大脑中提取相关的公式、性质、推论、图像、比例等知识和常见解题技巧.

2,通过解题实践，总结方程(组)解法

本题的各种解法有一个共同之处，那就是建立方程组，而解方程组恰恰就是大家的短板.因此，解决和匀变速直线运动有关的问题时，一定要树立方程组的数学思想，养成用数学思维亲自进行推算的习惯，不要嫌麻烦.尤其要注意通过类似本题的解法探究，不断总结方程和方程组的解法，这才是解决此类问题最常用的一把利器，也是今后研究物理问题必备的一种数学素养.

参考文献：

[1]王后雄. 教材完全解读( 高中物理必修2)[M].北京:中国青年出版社,2013(9).