同题异构，探求解题策略——以一道解析几何题的不同设问为例

朱 庆

(江苏省黄埭中学 215143)

教学的效益与问题设计的质量有很大的关系，教师应精选例题，充分挖掘例题的价值，教师应教会学生怎样审题，怎样对问题信息进行解构、重组、转化，进而寻找问题解决的突破口.同题异构是笔者在平时的教学活动中经常注意使用的方法，这样的教学可以从多角度、多层次启发学生的思维，促进知识的融会贯通，取得良好的教学效果.

数学中的问题主要分为三类：(1)“证明型”问题，这类问题要求证明某个问题成立；(2)“求值型”问题，这类问题要求找出满足某些条件的一个或所有的值；(3)“探究型”问题，这类问题要求证明一个命题或给出一个反例.

对于不同类型的数学问题，其解题策略不尽相同.下面笔者以一道解析几何题的不同设问为例，来谈谈如何选择较为合适的解题策略.

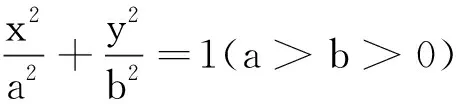
(1)求此椭圆的方程

(2)求证：对于所有满足条件的P、Q，线段PQ的垂直平分线过定点.

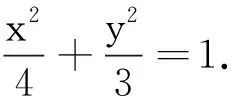
(2)分析这是一个“证明型”问题.此类问题中，从给定的信息入手，其目的是根据事先给出的信息推导出某个命题或计算出某个表达式的值.由于这类问题有清晰的目标，难度一般不大.

本例中，已知信息包括一个已知椭圆，一条已知直线，及椭圆上两个相关的未知点P、Q，这两个点的相关关系是它们的中点在已知直线上.目标是证明线段PQ的垂直平分线过一个定点.基本想法是选择恰当的参数把上述要点有效地表达出来，再进行整理运算.本题涉及两个不定点P、Q，及线段PQ的垂直平分线，除了设P、Q两点坐标外，不妨再增设中点T，结合点差法进而写出含参的线段PQ的垂直平分线的直线方程求解.

解设P(x1,y1),Q(x2,y2)，T(1,t).

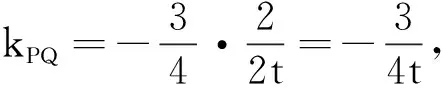
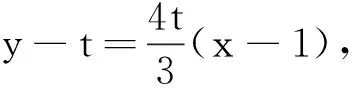
反思1 此题的问法更倾向于几何特征.几何问题代数化是解析几何的核心，运用代数方程的方法解决几何问题，在分析问题、解决问题的过程中要突出几何要素，注重几何要素的代数化，要在几何要素的引导下进行代数的恒等变形，要让几何图形帮助我们思考问题，确定恒等变形的方向.

反思2 线段的垂直平分线问题往往和线段中点及直线斜率有关，故用点差法将方程组变形，转化成共点的直线系方程问题，从而找出该定点.

如果教师对本题(2)的结论尝试以其他形式给出，问题又会怎样？

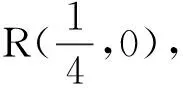
分析这是一个“求值型”问题.此类问题中，从已知条件出发，列出方程或方程组，利用消元法(单个元素或整体消元)，从而求出目标值.而本题中的P、Q两点都是不定点，导致RP、RQ的值也不是定值，给学生运算带来困惑，在运算的技巧上增加了难度.不过本题的解题策略还是清晰的，可设点P、Q坐标，从而列方程(组)，结合两点间距离公式，消元、化简、计算即可.

解设P(x1,y1),Q(x2,y2)

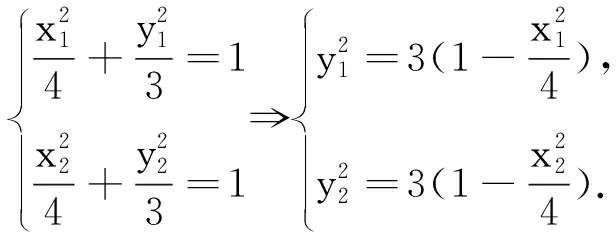
因为线段PQ的中点T在直线l：x=1上，

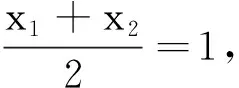
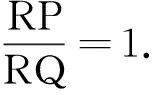
其变式RP=RQ，即R为线段PQ的垂直平分线上的一点，则R点的几何特征更为明显.

反思4 如果将满足条件的P、Q的某个位置记为一对，这样的点对有多少对？是有限对还是无穷多对？

像这样的多次追问，会使学生更积极地思考，参与讨论，进而对本题的几何特征有更深，更全面的了解，培养学生几何与代数互化的能力.

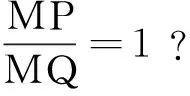
分析这是一个“探究型”问题.此类问题通常较难，因为我们必须先判断讨论的对象是否存在，再提供证明或举出反例.如果直接设M点坐标，用两点间距离公式表示去求解，所列式子较繁，运算量大，不一定能找到答案，基本上是半途而废.

解法1 将原式转化为MP=MQ，考察几何意义，发现M即为线段PQ的垂直平分线上的点，问题转化为原题(2).此题本质上是原命题的逆命题.

解法2 设M(m,n),P(x1,y1),Q(x2,y2),T(1,t).

由MP2=MQ2,得(x1-m)2+(y1-m)2=(x2-m)2+(y2-n)2,

即[(x1-m)2-(x2-m)2]+[(y2-n)2-(y1-n)2]=0.

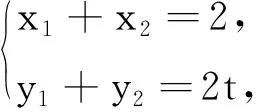
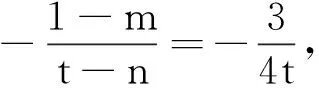
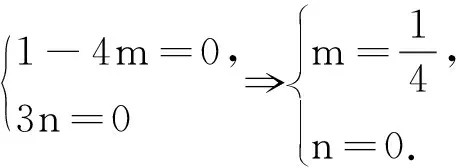
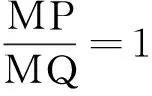
解法2是整理出m,n,t的关系式，利用关于t的恒成立问题得到解答.

反思6 由图形的对称性(PQ在第一象限和第四象限的图象关于x轴对称)可知，若存在定点M，则点M必在x轴上.故可设M(m,0),从而简化运算求解过程.

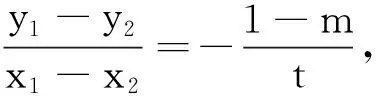
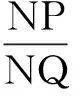
分析这类“探究型”问题增加了一个参数λ，而λ的值代表了线段NP、NQ的长度的比值.显然λ的值与N点的位置有关，如果顺着题意通过设点，列方程组求解的话，式子相当繁，含太多字母运算，找不到整理的头绪，属于难题.

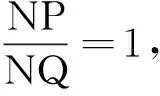
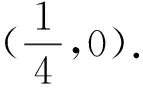
②当λ>0,λ≠1时，不存在定点N.

下面对情况②用反证法加以证明：

假设存在N，设N(m,n),

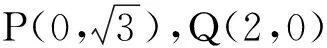
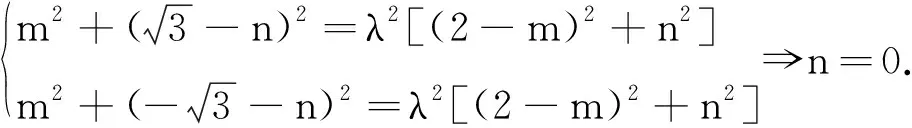
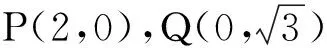
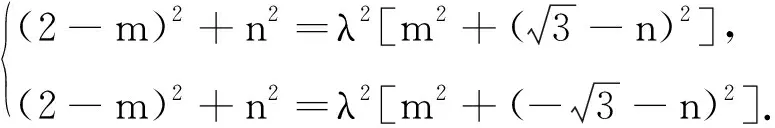
得(2-m)2=λ2(m2+3).

所以λ2=1，即λ=1(λ>0)，与λ>0,λ≠1矛盾.

所以当λ>0,λ≠1时，不存在定点N.

反思7 在解析几何问题中，由于点、直线等几何量的运动引起与之相应的某个(些)量的变化，然后探究这个(些)相关量的有关定点、定值问题，我们应教会学生运动变化的观点，并用这种运动变化的方法去探究几何性质，在“形”上有一个大概的体会，从而在解题过程中给我们以启发，最后再利用代数关系式定量计算，严密推导，得到解答.

反思8：对于不成立或不存在问题，通常可以举反例或用反证法加以证明.

参考文献：

[1]章建跃.数学学习与智慧发展(续)[J].中学数学教学参考(中旬)，2015(8).

[2]毛忠良.例谈问题探求中的信息解构与知识构建[J].中学数学教学参考：上旬，2015(11).