基于瞬态传热的含裂缝环形锻件传热模型

张玉存 田孟奇 李亚彬

燕山大学电气工程学院，秦皇岛，066004

0 引言

环形锻件是核电、石化等领域的关键基础部件，其成形质量直接影响装备的总体水平和可靠性，然而锻件中存在的锻造缺陷会影响锻件的成形品质［1］。对含缺陷锻件的传热模型进行研究，实时测量锻造过程中热态锻件的表面温度，作为定解条件代入传热模型，判断锻造过程中内部温度场的异常变化，及时有效地调整锻造工序，进而提高锻件的内部质量和锻造精度，可为锻件缺陷的定性识别提供理论支撑，对提高生产达标锻件的良品率和锻造的节能降耗具有重要的现实意义［2］。

近年来，国内外学者对包括环筒锻件在内的各种环形锻件温度场传热模型进行了大量的研究。范春利等［3］在热传导理论的基础上，针对含内部缺陷的锻件建立了二维传热模型，提出了一种求解得到锻件表面温度场以识别试件内部缺陷形状和位置的计算方法。沈功田等［4］应用红外热成像检测技术，对不同壁厚的碳钢管道内部和不同深度的壁厚减薄缺陷进行了加温或降温过程的红外热成像检测试验，指出材料热导率和厚度、温度激励方式是影响检测灵敏度的关键因素。关明等［5］、JANIK 等［6］通过试验模拟实际生产中的锻件，建立了Mn18Cr18N护环钢锻造中的温度场，对在一定保温措施下锻件的温度场变化情况进行了描述。崔晓龙等［7］在分析大型锻件传热的基础上建立了大型锻件的物理模型，并对其温度场的变化规律进行了对比分析，证明了热处理过程中数值模拟的可行性。王海亮等［8］针对内部含矩形缺陷试件，建立了二维物理和数学传热模型，通过有限体积法求解了瞬态温度场分布。CARLONE等［9］利用有限元仿真了钢的淬火过程，并成功揭示了温度场与固-固相变过程的内在关系。沈立华等［10］利用红外热像仪获得外壁温度，在简化一维模型下反推内壁温度，考虑了缺陷内空气对流换热及表面辐射对反推内壁温度的影响。曹春梅等［11］结合导热反问题，将红外检测得到的外壁温度作为强加边界条件，反推内壁热流密度和对流换热系数分布的普适解析级数解。上述研究是在一定理想假设条件下进行的，换热条件和物理场选择一维或二维条件下的稳态温度场，解析模型的缺陷边界大多为规则面。在锻造过程中，锻件表面的温度场与内部的结构、热物性及表面与外界环境的热交换是相互影响的。袁龙蔚［12-13］从缺陷体流变学理论上证明，锻造过程中由于裂缝塑性流变变形会形成温度场，裂缝处传热是连接锻件内部热传导和表面温度场之间过渡的一部分，是造成温度场非均匀性的原因之一。

本文通过理论分析方法构建锻件温度场传热模型，利用相应的数学物理方法计算温度场分布函数，通过传热模型直接明确地分析和表示裂缝条件下的锻件温度场，为锻造过程中裂缝的识别提供了理论计算方法；有限元仿真应用Comsol代入理论中的推导公式进行数值计算，验证理论计算的必要性；试验中，热像仪首次测量的表面温度为初始条件温度，作为附加定解条件代入传热模型，获得环形锻件温度场任一时刻、任一位置温度值的解析解，通过对比测量温度的相对误差分析试验精度，试验将测量温度近似作为真实温度；最后，应用MATLAB对裂缝表面温度值的解析解和测量温度进行拟合，观察各自的温度变化趋势，进一步验证传热模型的可行性。

1 含裂缝热态环形锻件传热模型的建立与求解

1.1 含裂缝热态环形锻件的传热规律

导热微元体始终遵循能量守恒定律，任一时间段均存在热平衡关系［14-15］。导入微元体总热流量与微元体内热源生成热的和等于导入微元体总热流量与微元体热力学能增量的和。如图1所示，在无内热源条件下，有

式中，Q为单位时间内传递的热量，即微元体热力学能增量；ρ、c分别为锻件的密度和质量热容；r为微元体半径。

对微元体的能量收支作热平衡分析，有

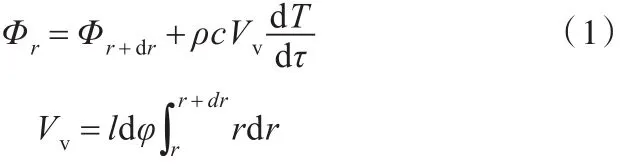
其中，Vv为微元体体积，其质量为 ρVv，dτ内温度升高所需的热量为 Φ(r+θdr)drdτ,θ∈(0,1)，质量热容c表示单位质量微元体升高单位温度所需热量。

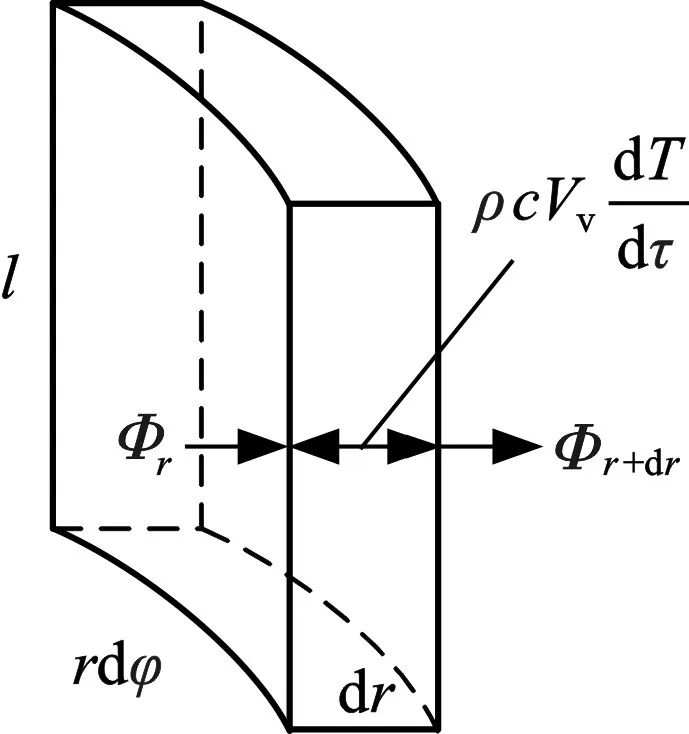
图1 柱坐标下微元体的导热、对流热平衡分析Fig.1 Analysis of thermal and convective heat balance of micro bodies under column coordinates

瞬态导热通过微元体的热流量随时间改变，式（1）等号右边第2项为微元体内部存在的热量蓄积。联系傅里叶导热定律、Robin边界条件，单位时间内由导热、对流通过微元曲面dS所传递的热量即热流量

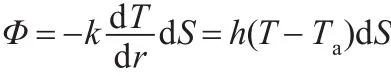
联立各热力学方程，可得关于微元体的热平衡关系：

其中，T、Ta分别表示材料温度和环境温度。假如微元体被加热，即材料温度高于裂缝处的空气温度，则视为热阻性缺陷。dT dτ为正值，T-Ta为负值，式（2）等号右边负号是为了对这一事实进行确认。由能量守恒得到的热平衡关系可知，锻件与环境的对流散热量约等于微元体内能的减少量，也可以通过集中参数法得出与式（2）基本一致的导热微分方程式。

1.2 含裂缝环形锻件传热模型的建立

应用推导的热平衡方程对锻件、裂缝的传热进行分析，建立锻件与裂缝的传热微分方程：

定解条件为

式中，Sw*、Sw、SL分别为环形锻件内外表面和裂缝边界面；hw*、hw、hL分别为环形锻件内外表面传热系数和裂缝表面传热系数；ρL、cL、VL分别为裂缝高温干空气的密度、质量热容和体积；ρ、c、V分别为锻件的密度、质量热容和体积；T、TL、Tf*、Tf分别为材料、裂缝以及环形锻件内外表面环境温度。

将得到的TL作为瞬态温度场的传热微分方程的Robin边界条件，结合实时测得的锻件表面温度，建立瞬态温度场的传热微分方程：

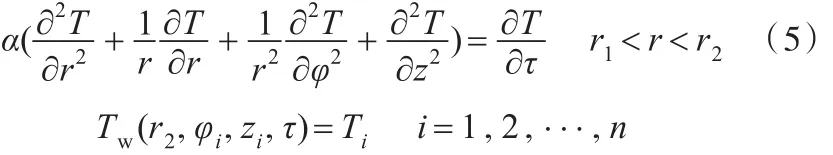
其中，锻件传热微分方程的外表温度Tw(r2,φi,zi,τ)由红外热像仪循环扫描获取。基于瞬态传热原理，裂缝对温度场的影响以传热函数的形式作为锻件温度场的Robin条件，考虑热流连续性，环形锻件裂缝Robin条件如下：

式中，h∆r为修正传热系数；k∆r为修正热导率裂缝边界面上温度的法向方向导数；nx、ny、nz分别为裂缝边界面上温度的法向方向余弦；kL为高温干空气热导率，其值见文献［15］；TL分别对 r、φ、z求偏导，是由坐标变换后复合函数求偏导的链式法则生成的。

对于式（6）中的修正传热系数，由于导热的瞬态热流量随时间而变化，故对相邻单位时间τ～τ+1内微元体的热流量进行分析：

为保证 l、dφ 有非零解，且 l≠0、dφ≠0 ，从而有

取

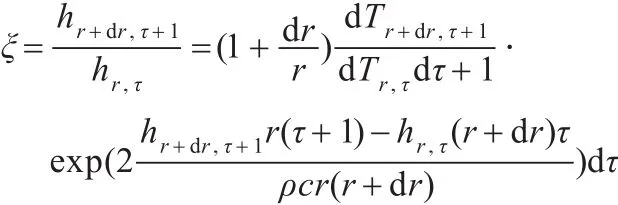
则单位面积的热流量为热流通量，瞬态导热时内部存在热量蓄积，热流通量与内部温度分布随时间而变化。

于是引入修正热物性参数的传热微分方程边界条件：

1.3 含裂缝热态环形锻件传热模型的求解

为简化参量和计算，取 F=hS(ρcV)，引入修正热物性参数：

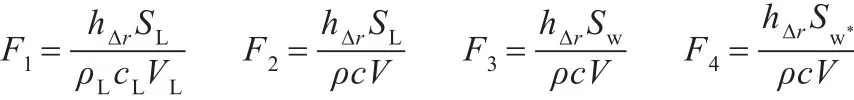
代入定解条件式（4），进一步求解裂缝的温度场函数：

从对流换热微分方程组出发，联系自然对流换热的准则方程：Nu=C(GrPr)m(L δ)n，计算对流传热系数h=Nuk δ，其中，Nu为努塞尔数，Pr为普朗特数，k为流体热导率，可得对流传热系数的表达式：

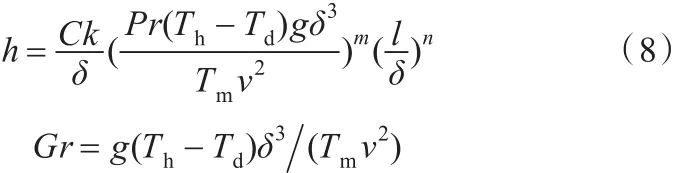
传热系数是与锻件温度相关的函数，Th、Td分别表示对流面的高温函数和低温函数，对于环形锻件外表面，对应表示外表面温度Tw、外侧环境温度Tf；Tm为外表面与外侧环境的平均温度。

将热流量作为内外表面温度的中间变量，分离变量并积分，代入傅里叶导热定律，可得锻件温度与内表面温度关系：

当半径r→r2，温度T→Tw时，可得锻件内外表面温度关系：Tw*=Tw-r2(ln r2-ln r1)dT dr。根据上式计算锻件内侧温度作为Th代入式（8）重新定义热物性参数并计算，得到内表面环境温度函数：

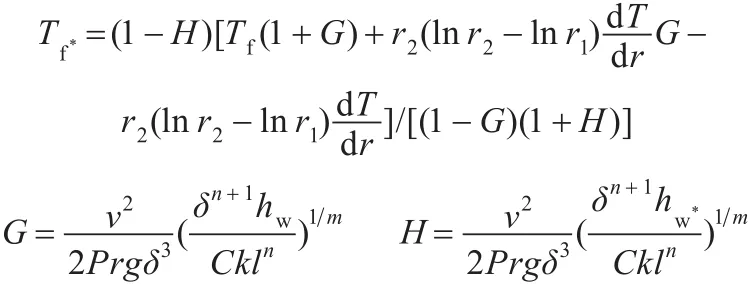
其中，C、m、n参照努塞尔数 Nu；Pr、v、k的取值见文献［15］。内侧环境温度函数Tw*代入裂缝的温度场函数TL，进而使函数的热物性参数变量减小。

最后，为了分离变量以求解偏微分方程，定解条件中的Robin非齐次边界条件需转化成齐次形式，考虑其边值函数与时间τ无关，作满足空间变量 r的辅助函数［16-17］：Tb(r)=(ar+b)Tf+(cr+d)Tf*。辅助函数的选取有一定任意性，形式、构造方法不唯一，在满足确定的齐次边界条件和齐次泛定方程条件下，经计算结果是一致的，代入边界条件式（7），由对应系数相等解待定系数a、b、c、d。令ζ=T-Tb，代入泛定方程并确定相应参数，使得关于ζ的定解问题具有齐次边界条件和齐次的泛定方程。代入边界条件式（7），得到关于ζ的齐次边界条件式及最终的辅助函数：

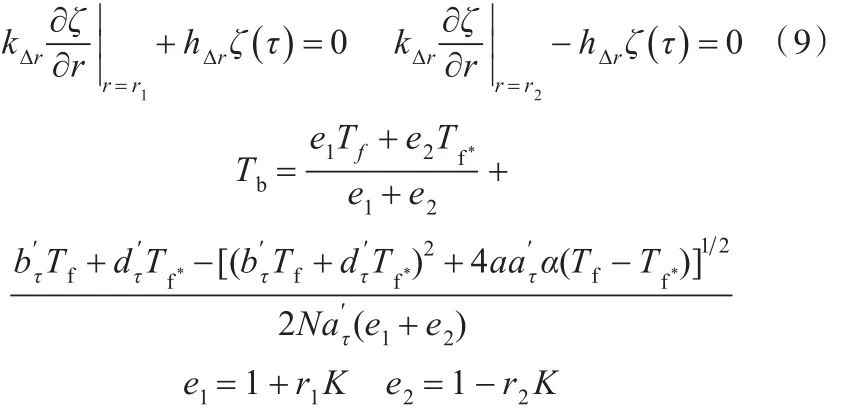
应用分离变量法求解温度场传热微分方程，各待定系数、积分常数可以通过代入裂缝边界条件、传热微分方程定解条件及特征函数的正交性来确定，迭加分离方程基本解可以得到锻件温度场函数的完全解［18］：

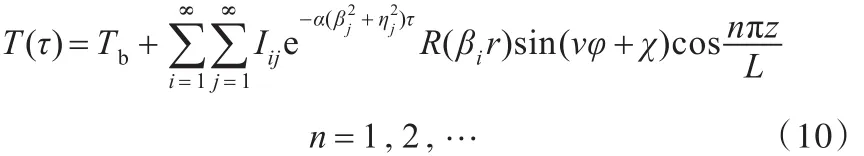
其 中 ，ω2=β2+η2为 假 设 常 量 符 合 关 系 ，N=1 K。分离方程 R(βir)可改写为v阶贝塞尔微分方程的 标 准 解 形式：R(βir)=C1Jv(βir)+C2Yv(βir)，Jv(βir)、Yv(βir)分别为第一类、第二类贝塞尔通解函数。

联系初始条件 ζ(r,φ,z)|τ=0=T0-Tb，代入附加边界条件 T(φi,zi,τ)|r=r2=Tw(τ)，可确定式（10）中的系数 Iij，即

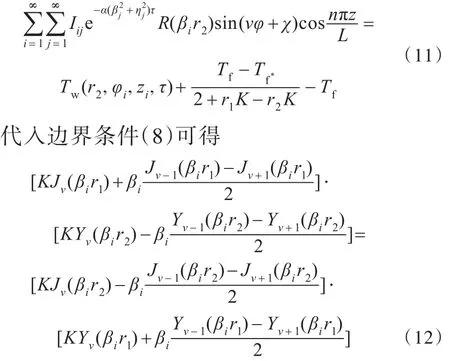
其中，Jv+1(βir)、Jv-1(βir)、Yv+1(βir)、Yv-1(βir)是由贝塞尔函数的微分性质［19］推导的导数与阶次v间的微分关系和递推公式。联系v阶贝塞尔微分方程的通解函数可得对应的通解表达式。代入裂缝边界条件：

联系式（12）可确定 βi值以及最终的含裂缝环形锻件温度场传热模型：

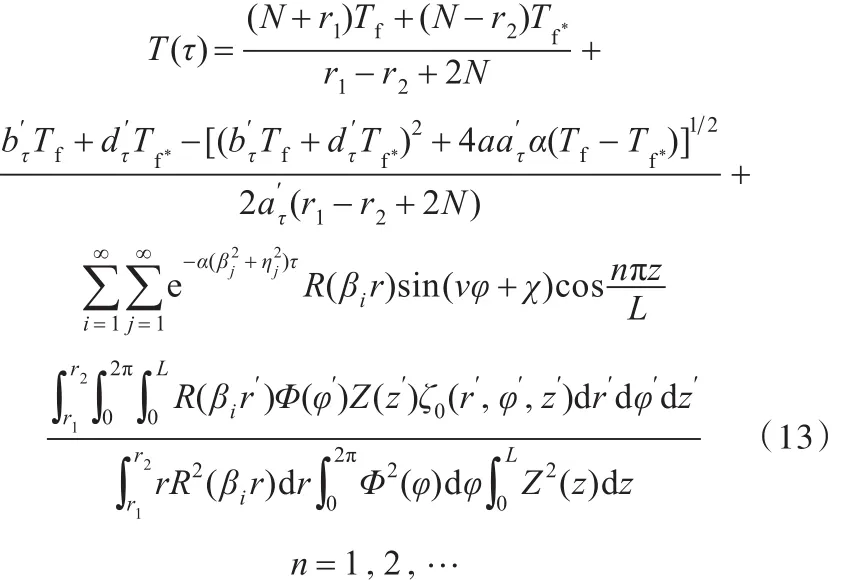
2 试验验证

2.1 仿真分析

应用Comsol有限元软件建立上文理论设定条件下的计算模型，对热态环形锻件的瞬态传热进行仿真，获取含裂缝环形锻件的温度场分布，提取全方向角的轴向多点表面温度数据。应用Comsol分析含裂缝环形锻件的传热性质时，考虑有限元计算需足够精细化网格，同时保证合理的计算时间，选取如下尺寸的环形锻件进行仿真。轴向高度为0.5 m，内外径分别为0.30 m、0.24 m，裂缝尺寸为深度0.015 m（近表）～0.03 m（环壁中心）、宽度1～3 mm，高度0.1 m，其他参数同上文。全方向角、不同轴向高度仿真温度分布数据见表1。

表1 环形锻件表面的不同高度的圆周上仿真温度分布数据Tab.1 The temperature distribution data on the circumference of the different heights of the ring forging surface

由表1可以看出，环形锻件上出现了一些温度低于正常温度的数据（用黑体表示），通过选取一维绘图组对不同尺寸裂缝的温度数据进行具体分析。同一时刻条件下，内外环境温度不同条件下的外表温度曲线见图2。考虑环形锻件内外环境温差，对于较小或较大尺寸的裂缝，在红外检测最小分辨率内的温度变化幅度更加明显。

同一时刻下，考虑环形锻件内外环境温差，对比裂缝边界不同条件下的外表温度曲线见图3。可以看出，环形锻件的裂缝边界为对流时，对于较小或较大尺寸的裂缝，在红外检测最小分辨率内的温度变化幅度更加明显。

综上所述，考虑热态环形锻件内外环境温差和裂缝边界的有限空间自然对流，对于较小或较大尺寸裂缝的识别是必要且可行的。对比图2、图3可以得出，毫米数量级的裂缝宽度具备一定的识别度，裂缝宽度为1 mm时区分已不明显，即常规计算条件下微米数量级宽度的裂缝已较难识别。为了明确显示表面温度变化，应用MATLAB对仿真所得的环件表面温度数据进行简单的消噪、精简处理，用环件表面展开的曲面温度分布图表示，见图4。

图2 内外环境温度不同条件下的外表温度曲线Fig.2 Internal and external ambient temperature under different conditions of the surface temperature curve

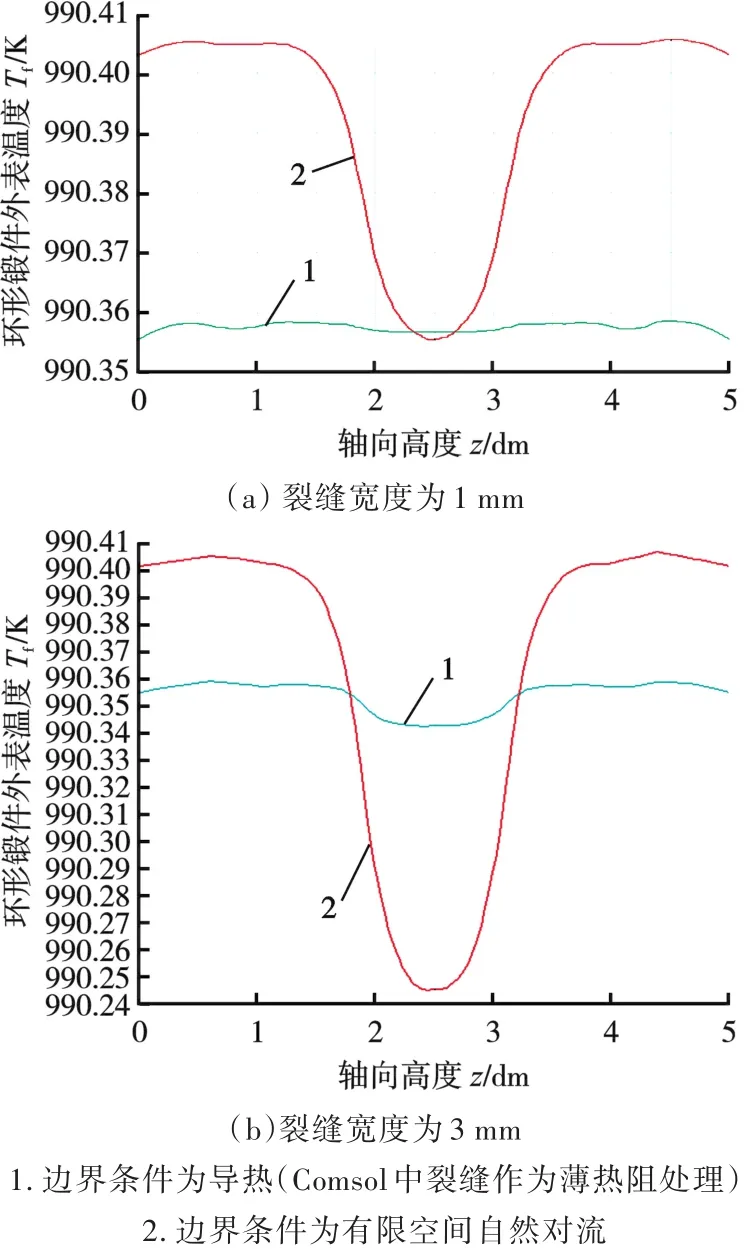
图3 对比裂缝边界不同条件下的外表温度曲线Fig.3 Curve of external surface temperature under different conditions of fracture boundary

图4 裂缝对应表面的曲面温度分布图Fig.4 The surface temperature distribution of thecorresponding surface of the crack

图4 中，参照xy坐标以及右侧反色表，分析缺陷的方位角、轴向高度可知裂缝的大致形态及位置。锻件在轴向0.2～0.3 m间温度出现较大的区域性波动，且弧度范围内任意轴向截面大致呈沟状降低。温度越高，高温干空气热导率越大，锻件热导率越小，高温干空气的热导率远小于热态锻件的热导率，为热阻性缺陷。

2.2 试验

为了验证瞬态传热理论所得瞬态温度场传热模型的可行性，选取含裂缝热态环形锻件作为试件，锻件和裂缝尺寸参数同上文。试验中，红外热像仪镜头与被测锻件的直线距离为5 m，垂直距离为0.5 m。应用SRJX-8-13箱式电阻炉加热环形锻件，加热至1 000℃后取出置于滚动台上，调试红外热像仪对锻件表面温度进行检测，锻件表面的红外热图像见图5。

图5 含裂缝热态环形锻件热像图Fig.5 Thermal image with cracks for hot ring forgings

此时，可以准确获取任一时刻下环形锻件表面温度场，某一时刻的表面3D温度场见图6。运用IRBIS 3 professional导出裂缝对应表面的轴向温度值，选取不同轴向高度、π方向角上解析解与测量温度、仿真温度进行比较，见表2。

图6 锻件表面3D温度场分布Fig.6 Forging surface 3D temperature field distribution

表2 不同轴向高度、π方向角上解析解与测量温度、仿真温度的比较Tab.2 Different axial height，the direction of the angle analysis and measurement of temperature，simulation temperature comparison

分析表2中数据可知，解析解与测量温度、仿真温度与测量温度的最大相对误差分别为0.24%、0.31%，瞬态传热理论计算的传热模型解析解满足精度要求（解析解是将热像仪首次扫描环形锻件表面温度作为初始温度信息和其他定解条件代入传热模型求解的），验证了传热模型的正确性；基于理论推导公式与边界条件设定下的Com⁃sol仿真结果满足精度要求，验证了仿真分析的可行性。为了进一步验证传热模型的可行性，应用MATLAB对表2中环形锻件表面温度数据进行拟合，对比曲线见图7。图7中，裂缝边缘存在局部温度升高的区域性波动，符合缺陷体流变学理论。

综上所述，传热模型解析解与试验测量温度的变化趋势大致相同；同时，解析解与试验测量温度、仿真温度与试验测量温度的相对误差满足精度要求，仿真的有限元计算建立在理论推导公式的基础之上，说明传热模型可以通过热像仪获取外表面温度为初始条件下，实现对热态环形锻件内裂缝的识别。

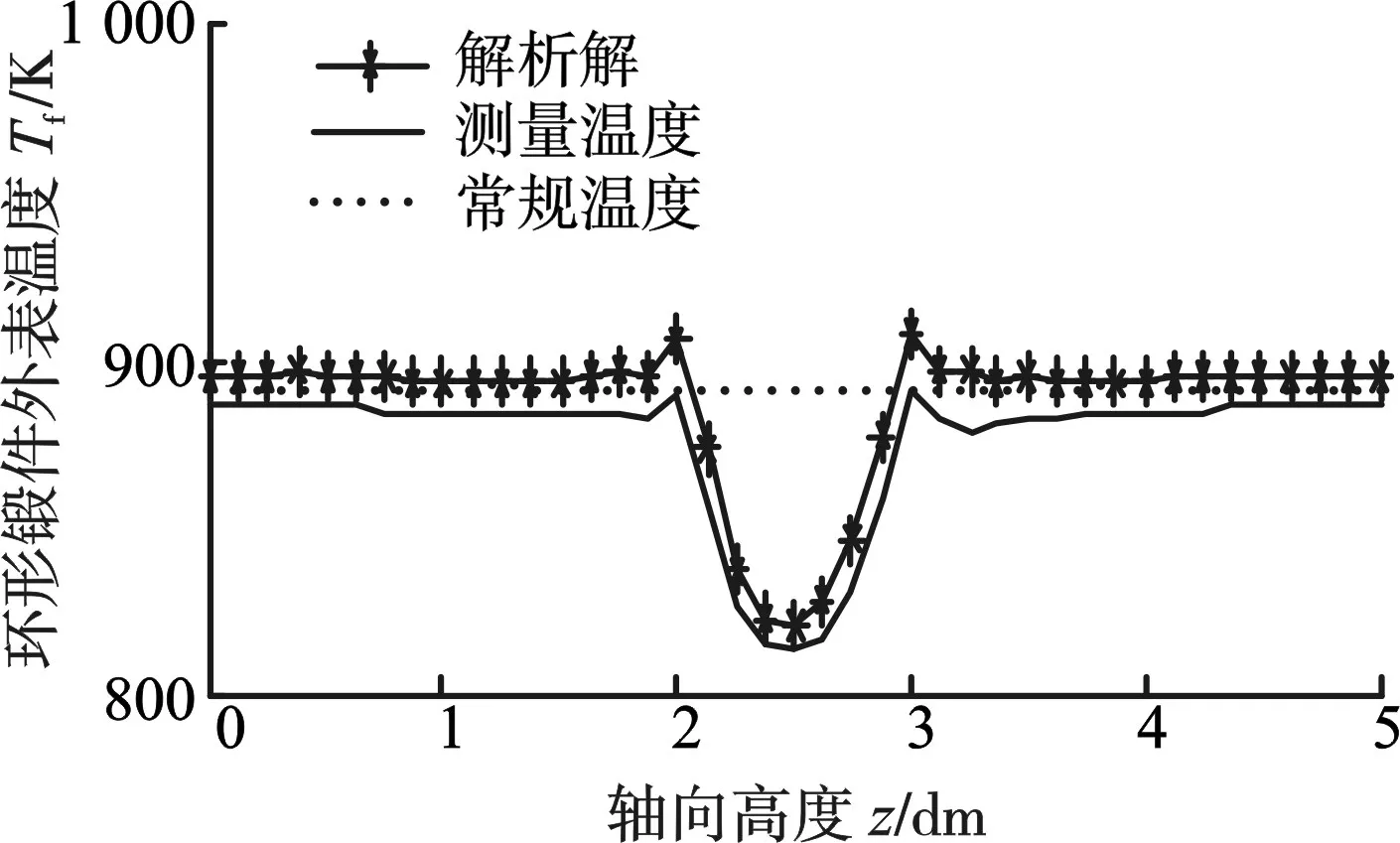
图7 裂缝对应表面的轴向温度变化Fig.7 Cracks correspond to the axial temperature changes of the surface

3 结语

相对于一般边界条件设定常量的处理方法，考虑热态环形锻件内外环境温差和裂缝边界的有限空间自然对流，对于较小或较大尺寸的裂缝都具有更好的识别度，证明了理论计算的必要性。试验中，传热模型解析解、仿真温度分别与试验数据的对比结果满足相对误差的精度要求，验证了传热模型和仿真分析的可行性。

［1］ 任运来，聂绍珉，牛龙江，等.大型锻件内部空洞缺陷修复条件［J］.机械工程学报，2008，44（2）：248-252.REN Yunlai，NIE Shaomin，NIU Longjiang，et al.Res⁃toration Conditions of Hollow Voids in Large Forgings［J］.Journal of Mechanical Engineering，2008，44（2）：248-252.

［2］ 戴文远，李长有.红外定量检测缺陷的热传导理论分析模型［J］.红外，2014，34（4）：43-46.DAI Wenyuan，LI Changyou.We Theoretical Model of Heat Conduction Theory for Infrared Quantitative De⁃tection Defects［J］.Infrared，2014，34（4）：43-46.

［3］ 范春利，孙丰瑞，杨立.基于红外测温试件内部缺陷的识别算法研究［J］.工程热物理学报，2007，28（2）：304-306.FAN Chunli，SUN Fengrui，YANG Li.Study on Recog⁃nition Algorithm of Internal Defects Based on Infrared Thermometry［J］.Journal of Engineering Thermophys⁃ics，2007，28（2）：304-306.

［4］ 沈功田，李涛，姚泽华.高温压力管道红外热成像检测技术［J］.无损检测，2002，24（11）：473-477.SHEN Gongtian，LI Tao，YAO Zehua.Infrared Ther⁃mal Imaging Detection Technology for High Tempera⁃ture Pressure Pipes［J］.Nondestructive Testing，2002，24（11）：473-477.

［5］ 关明，付赟秋，常志梁，等.大锻件锻造过程中温度场测定及其结果分析［J］.锻压技术，2012，37（2）：6-9.GUAN Ming，FU Yunqiu，CHANG Zhiliang，et al.De⁃termination of Temperature Field and Its Results in Forging Process of Large Forgings［J］.Forging Technol⁃ogy，2012，37（2）：6-9.

［6］ JANIK M，DYJA H.Modelling of Three-dimensional Temperature Field Inside the Mould during Continu⁃ous Casting of Steel［J］.International Journal of Heat and Mass Transfer，2004，20：177-182.

［7］ 崔晓龙，万妮丽.大型锻件热处理过程的数值模拟研究［J］.热处理，2005，20（4）：12-16.CUI Xiaolong.WAN Nili.Study on Numerical Simula⁃tion of Heat Treatment Process for Large Forgings［J］.Heat Treatment，2005，20（4）：12-16.

［8］ 王海亮，范春利，孙丰瑞，等.二维内部缺陷的红外瞬态定量识别算法［J］.红外与激光工程，2012，41（7）：1714-1720.WANG Hailiang，FAN Chunli，SUN Fengrui，et al.In⁃frared Transient Quantitative Recognition Algorithm for Two-dimensional Internal Defects［J］.Infrared and Laser Engineering，2012，41（7）：1714-1720.

［9］ CARLONE P，PALAZZO G S，PASQUINO R.Finite Element Analysis of the Steel Quenching Process：Temperature Field and Solid-solid Phase Change［J］.Computers&Mathematics with Applications，2010，59（1）：585-594.

［10］ 沈立华，范春利，杨立，等.缺陷对红外测温反推内壁温度的影响分析［J］.红外技术，2005，27（3）：250-253.SHEN Lihua，FAN Chunli，YANG Li，et al.Influence of Defects on Inverted Temperature Measurement by Inferred Wall Temperature［J］.Infrared Technology，2005，27（3）：250-253.

［11］ 曹春梅.圆筒内壁热流密度和对流换热系数的红外热诊断研究［J］.激光与红外，2007，37（9）：849-851.CAO Chunmei.Infrared Thermal Diagnosis of Heat Flux and Convection Heat Transfer Coefficient in Cyl⁃inder Wall［J］.Laser and Infrared，2007，37（9）：849-851.

［12］ 袁龙蔚.带缺陷流变性材料裂尖断裂过程区的热力学性和电磁性［J］.湘潭大学自然科学学报，1997，19（3）：29-37.YUAN Longyu.Thermodynamic and Electromagnetic Properties of Fracture Tip Fracture Zone in a Rheolog⁃ical Material with Defects［J］.Natural Science Jour⁃nal of Xiangtan University，1997，19（3）：29-37.

［13］ 袁龙蔚.缺陷体流变学——Ⅱ.裂缝萌生区的平衡与演化以及缺陷体位移场［J］.湘潭大学自然科学学报，1997，19（3）：39-55.YUAN Longyu.Rheology of Defective Bodies—II.Balance and Evolution of Crack Initiation Zone and Displacement Field of Defect［J］.Natural Science Journal of Xiangtan University，1997，19（3）：39-55.

［14］ 涂虬.热平衡法在传热学教学中的应用［J］.武汉工程职业技术学院学报，2000，12（1）：63-67.TU Qiu.Application of Thermal Balance Method in Teaching of Heat Transfer［J］.Journal of Wuhan En⁃gineering Institute，2000，12（1）：63-67.

［15］ 陶文铨.传热学［M］.西安：西北工业大学出版社，2006：272-277.TAO Wenquan.Heat Transfer［M］.Xi’an：Northwest⁃ern Polytechnical University Press，2006：272-277.

［16］ 严镇军.数学物理方程［M］.合肥：中国科学技术大学出版社，1996：68-74.YAN Zhenjun.Equations of Mathematical Physics［M］.Hefei：University of Science&Technology Chi⁃na Press，1996：68-74.

［17］ 傅立叶.热的解析理论［M］.桂质亮，译.北京：北京大学出版社，2008.FU Liye.Light Translation.Analytical Theory of Heat［M］.Gui Zhiliang，Trans.Beijing：Peking University Press，2008.

［18］ 张玉存，张雷强，付献斌.热态轴类含空洞锻件内部温度场分布［J］.中国机械工程，2015，26（19）：2672-2676.ZHANG Yucun，ZHANG Leiqiang，FU Xianbin.Analyses of Interior Temperature Field Distribution for Hot Axial Forgings with Void［J］.China Mechani⁃cal Engineering，2015，26（19）：2672-2676.

［19］ 克罗克斯顿.数学物理方程导论［M］.载安英，译.北京：高等教育出版社，1982：275-282.Croxton.Introduction to Equations of Mathematical Physics［M］.Zai Anying，Trans.Beijing：Higher Edu⁃cation Press，1982：275-282.